Similar presentations:
Поворот
1.
Поворот2.
«Без движения —жизнь только
летаргический
сон».
Жан Жак Руссо
3.
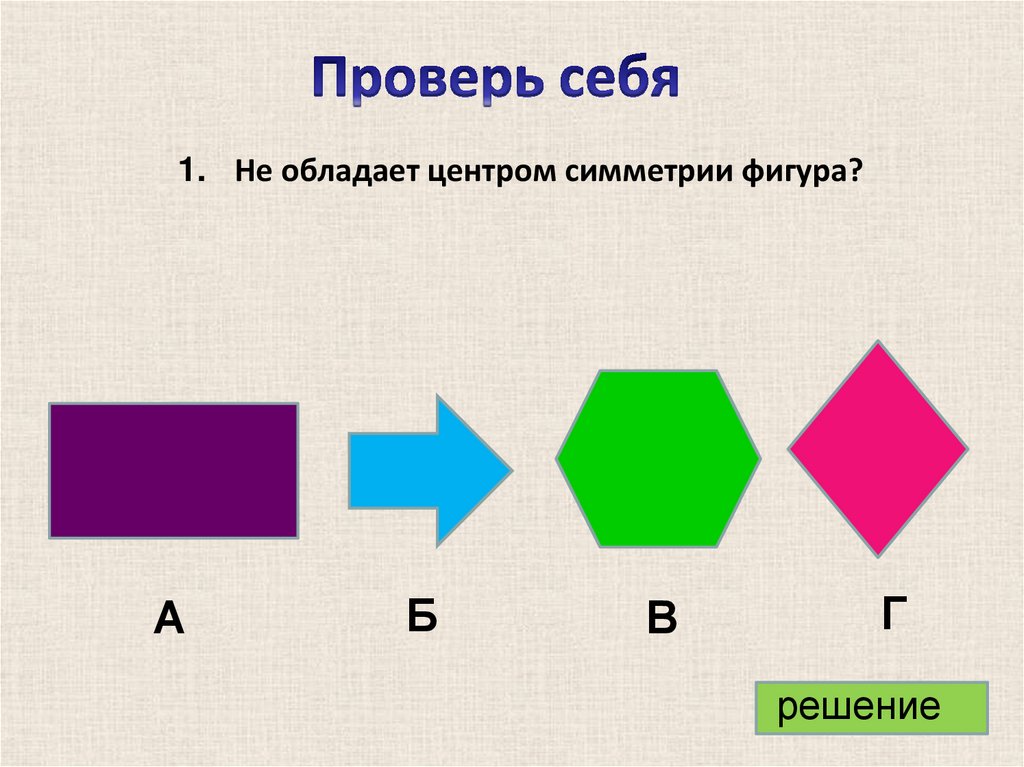
1. Не обладает центром симметрии фигура?А
Б
В
Г
решение
4.
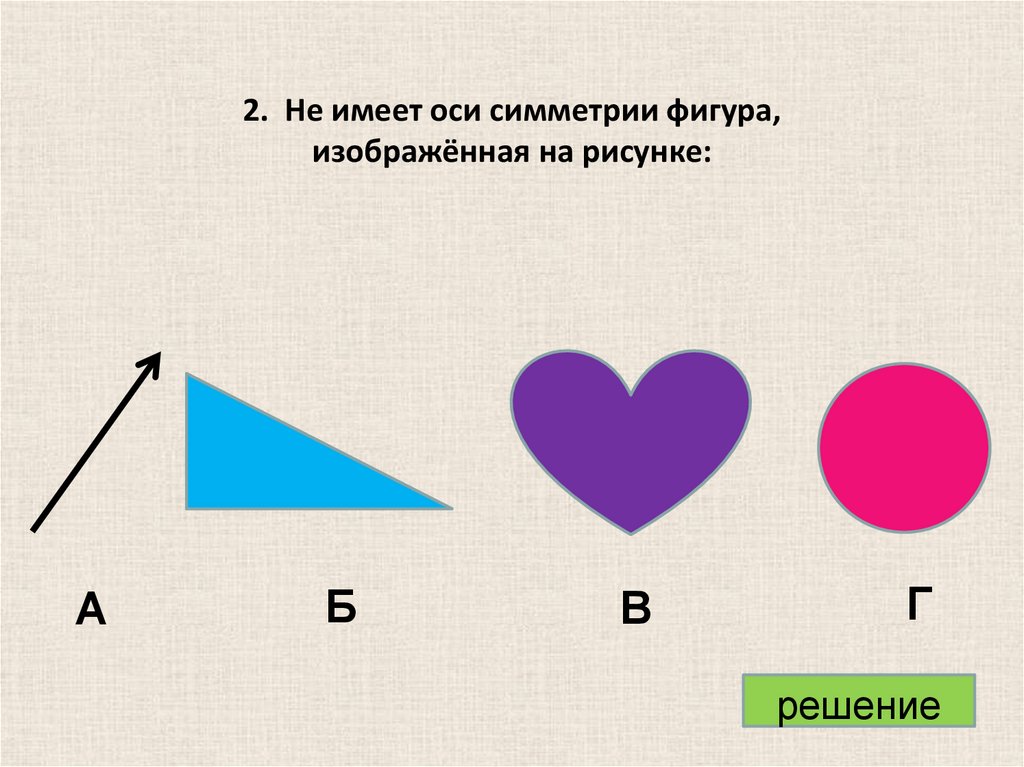
2. Не имеет оси симметрии фигура,изображённая на рисунке:
А
Б
В
Г
решение
5.
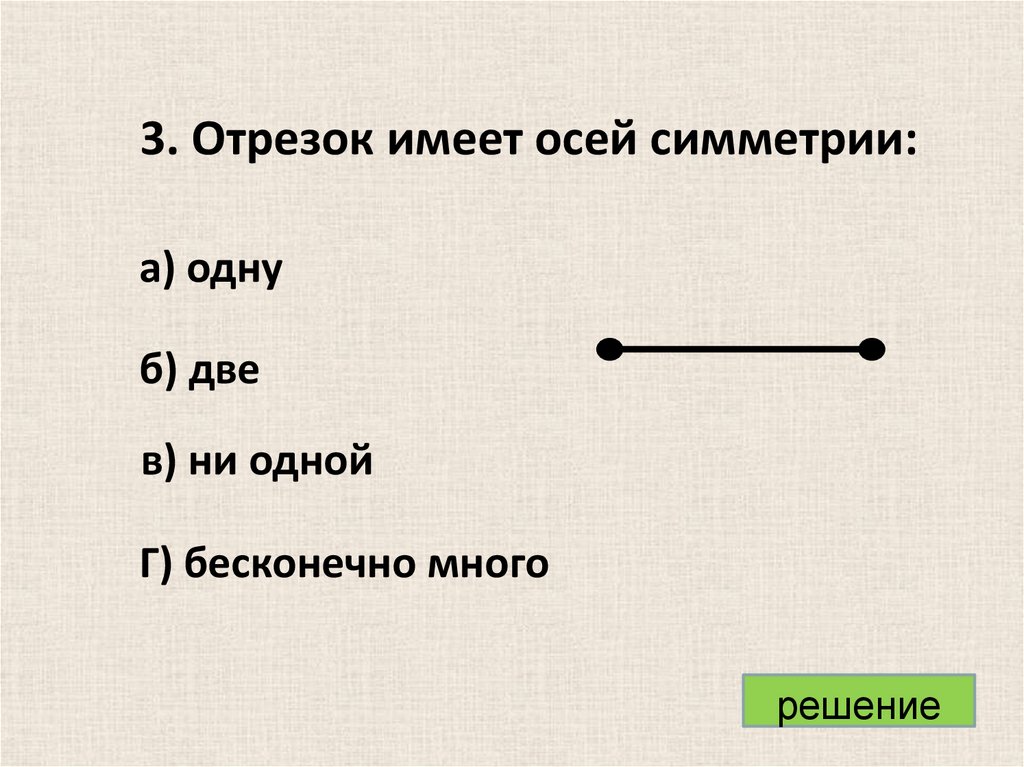
3. Отрезок имеет осей симметрии:а) одну
б) две
в) ни одной
Г) бесконечно много
решение
6.
4. Центр симметрии имеет:а) параллелограмм;
б) равносторонний треугольник;
в) трапеция;
Г) правильный пятиугольник.
решение
7.
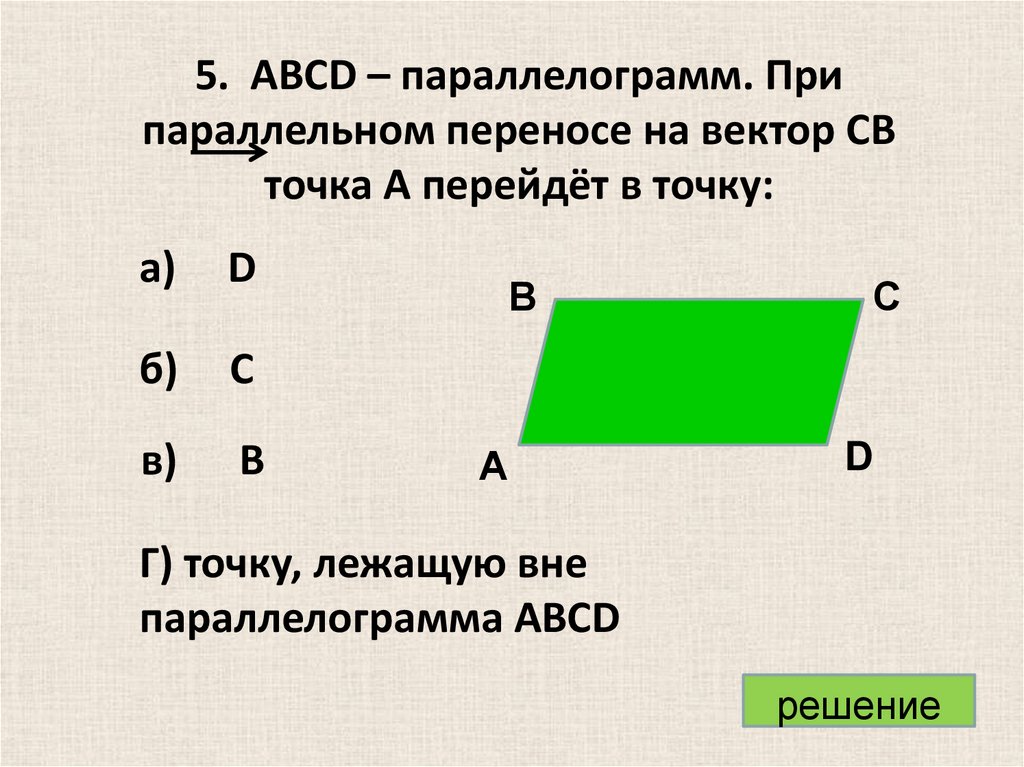
5. ABCD – параллелограмм. Припараллельном переносе на вектор CB
точка A перейдёт в точку:
а)
D
б)
C
в)
B
В
А
С
D
Г) точку, лежащую вне
параллелограмма ABCD
решение
8.
6. При осевой симметрии прямая,проходящая через ось симметрии будет
отображаться на:
а) параллельную ей прямую
б) перпендикулярную ей прямую
в) себя
г) отрезок
решение
9.
7. Точка A имеет координаты: x= - 5; y= 4. Тогда точка C,симметричная точке A относительно
оси x, будет иметь координаты:
) x= -5; y=- 4;
Б) x= 5; y=- 4;
В) x= 5; y= 4;
Г)
x= 4; y= -5;
решение
10.
8. При движении ромботображается на:
а) параллелограмм
б) квадрат
в) произвольный четырёхугольник
г) ромб
решение
11.
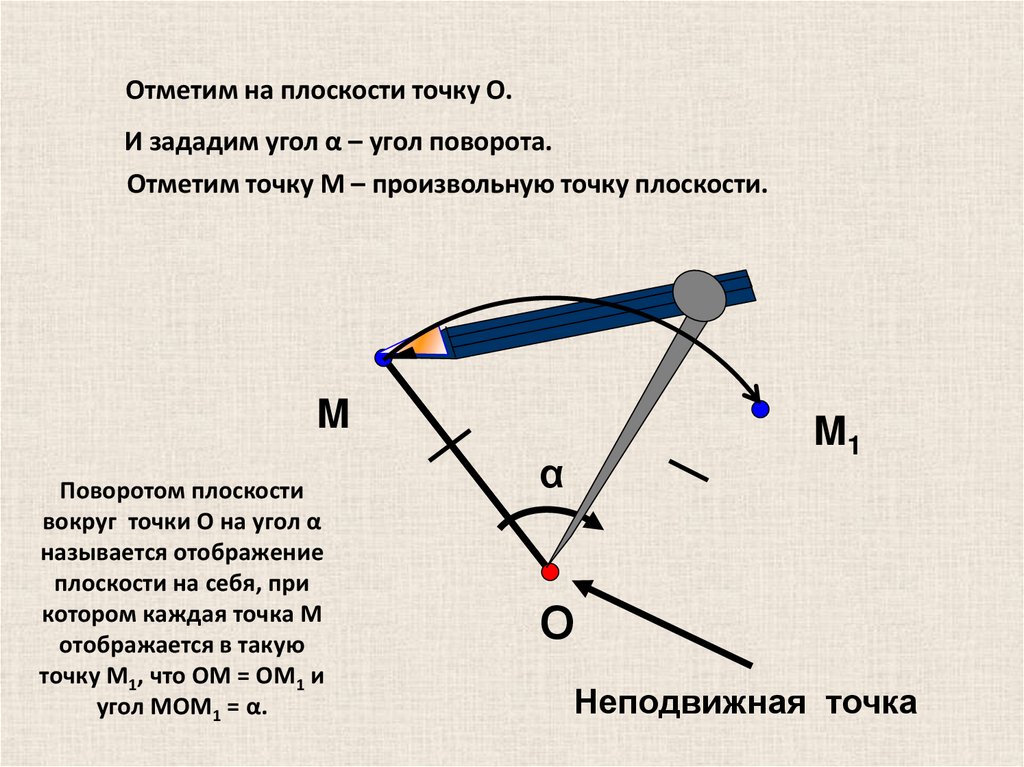
Отметим на плоскости точку О.И зададим угол α – угол поворота.
Отметим точку M – произвольную точку плоскости.
M
Поворотом плоскости
вокруг точки О на угол α
называется отображение
плоскости на себя, при
котором каждая точка M
отображается в такую
точку M1, что OM = OM1 и
угол MOM1 = α.
M1
α
О
Неподвижная точка
12.
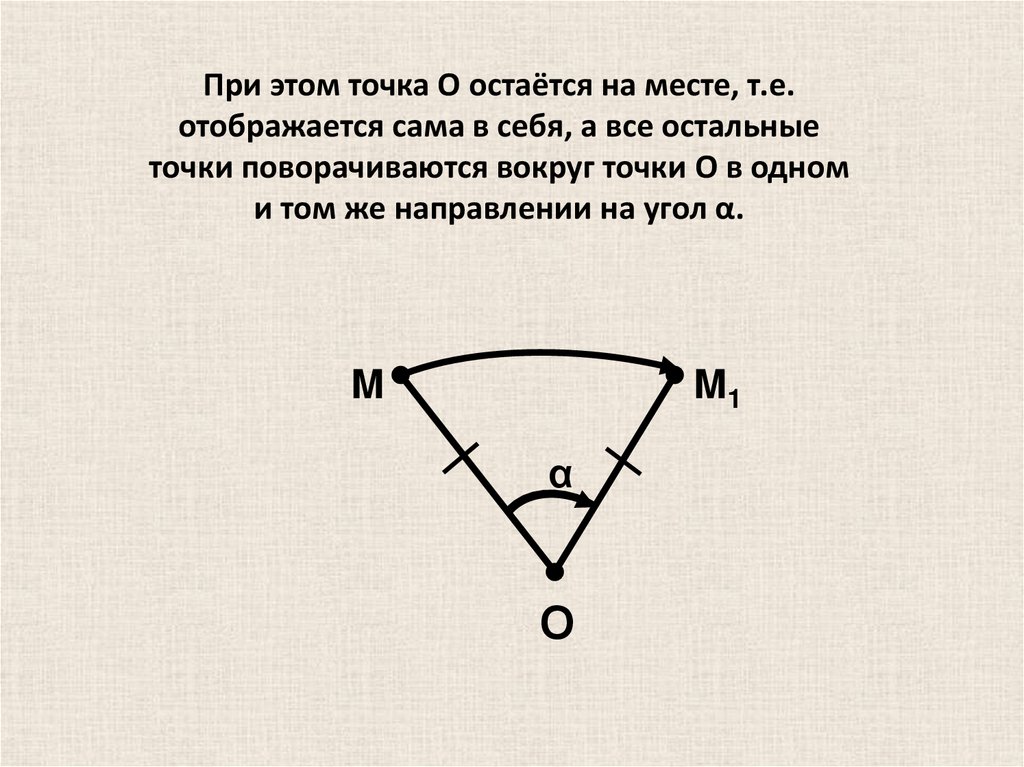
При этом точка O остаётся на месте, т.е.отображается сама в себя, а все остальные
точки поворачиваются вокруг точки O в одном
и том же направлении на угол α.
M
M1
α
О
13.
Точка О называется центром поворота,α – угол поворота.
Обозначается
P.O
M
α
M1
О
Центр поворота
14.
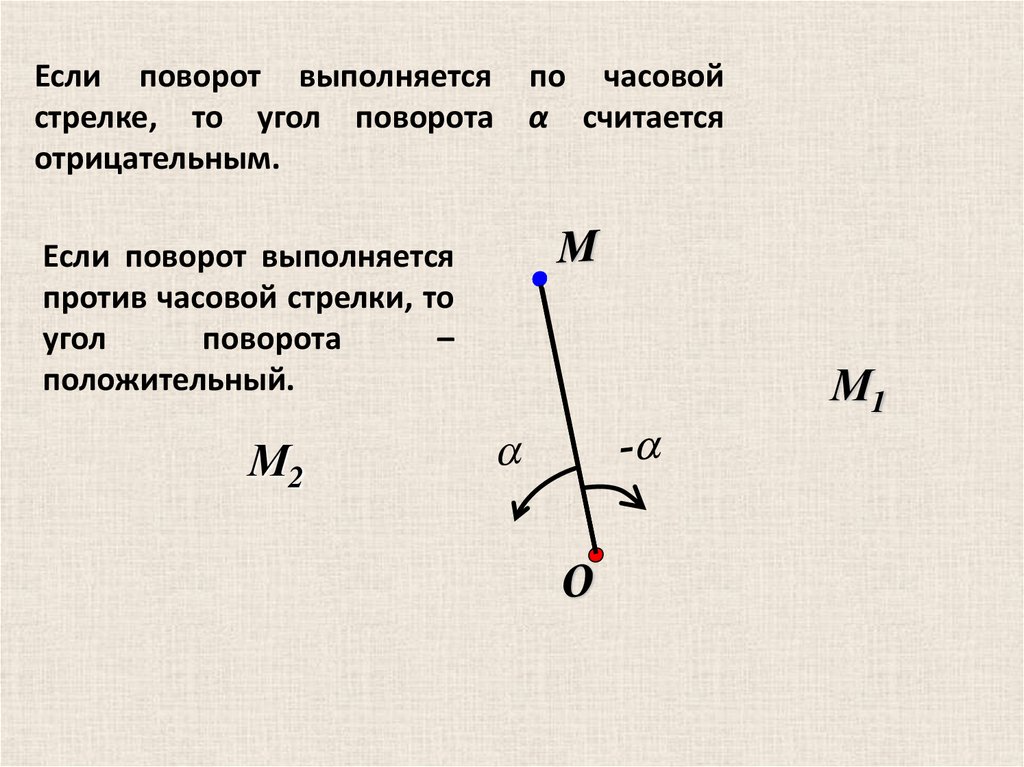
Если поворот выполняется по часовойстрелке, то угол поворота α считается
отрицательным.
Если поворот выполняется
против часовой стрелки, то
угол
поворота
–
положительный.
М2
М1
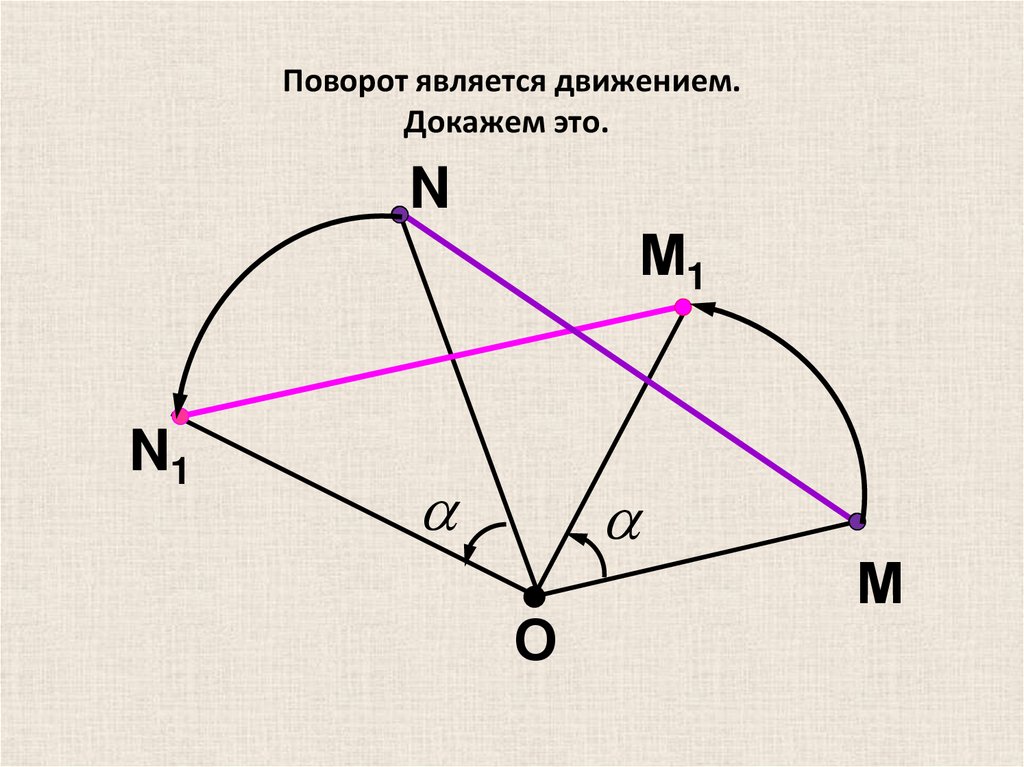
15. Поворот является движением. Докажем это.
NМ1
N1
О
М
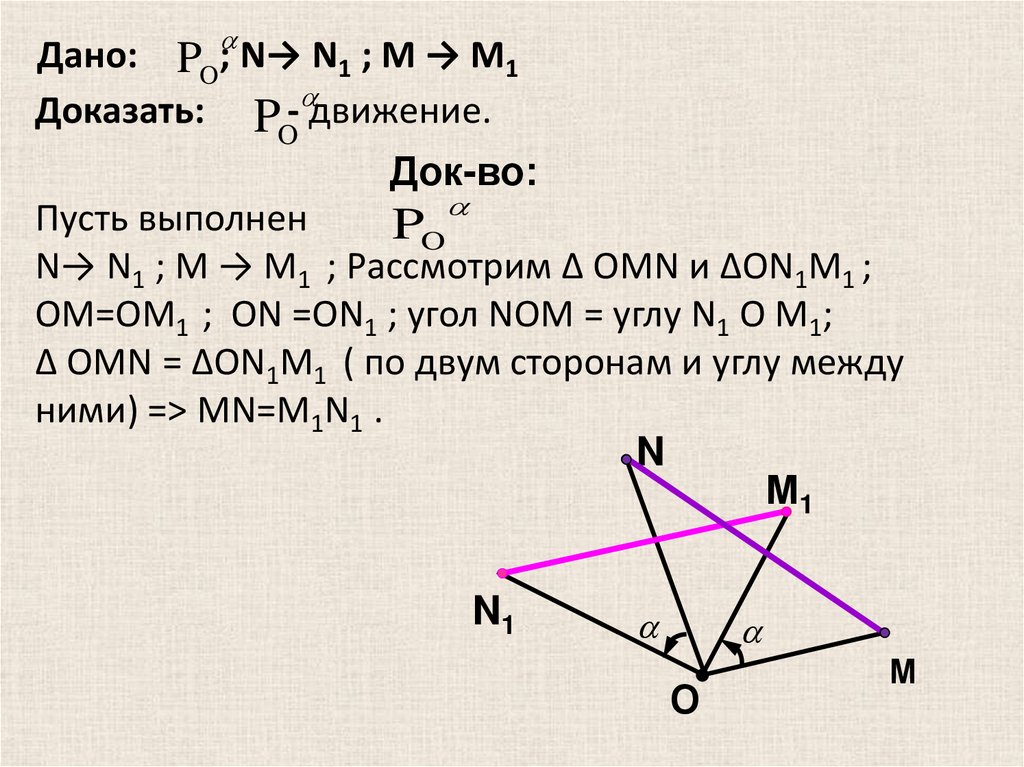
16. Дано: ; N→ N1 ; M → М1
Дано: PO ; N→ N1 ; M → М1Доказать: P - движение.
O
Док-во:
Пусть выполнен
PO
N→ N1 ; M → М1 ; Рассмотрим ∆ OMN и ∆ON1М1 ;
OM=OМ1 ; ON =ON1 ; угол NOM = углу N1 O М1;
∆ OMN = ∆ON1М1 ( по двум сторонам и углу между
ними) => MN=М1N1 .
N
М1
N1
О
М
17.
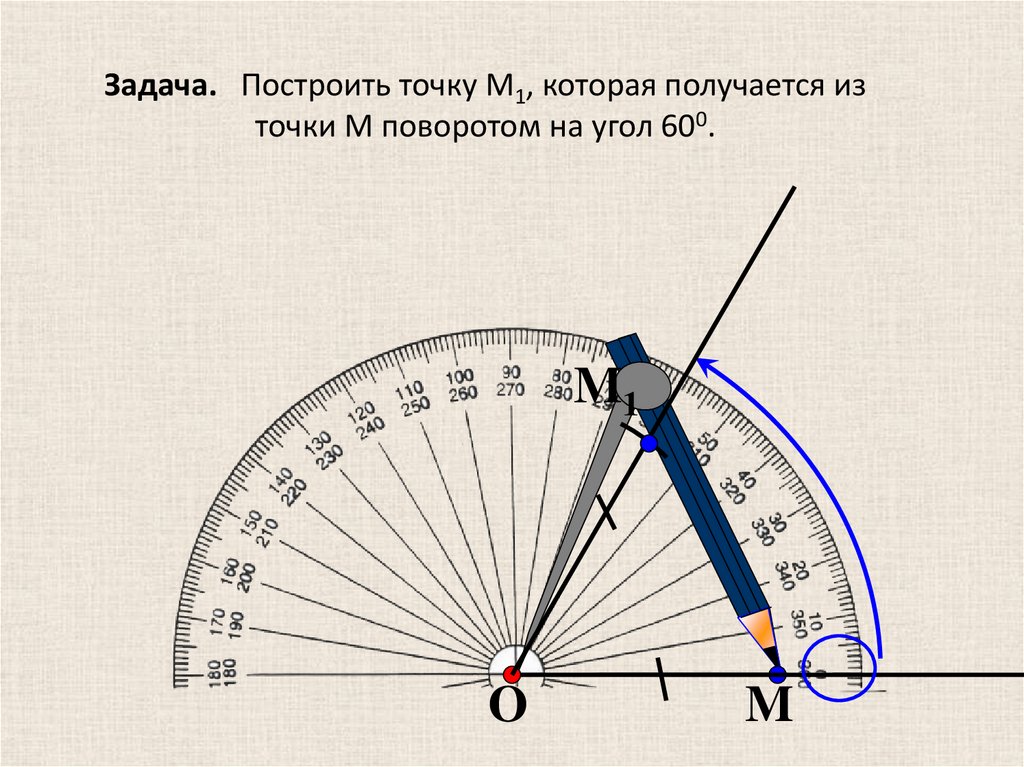
Задача. Построить точку M1, которая получается източки M поворотом на угол 600.
M1
O
M
18.
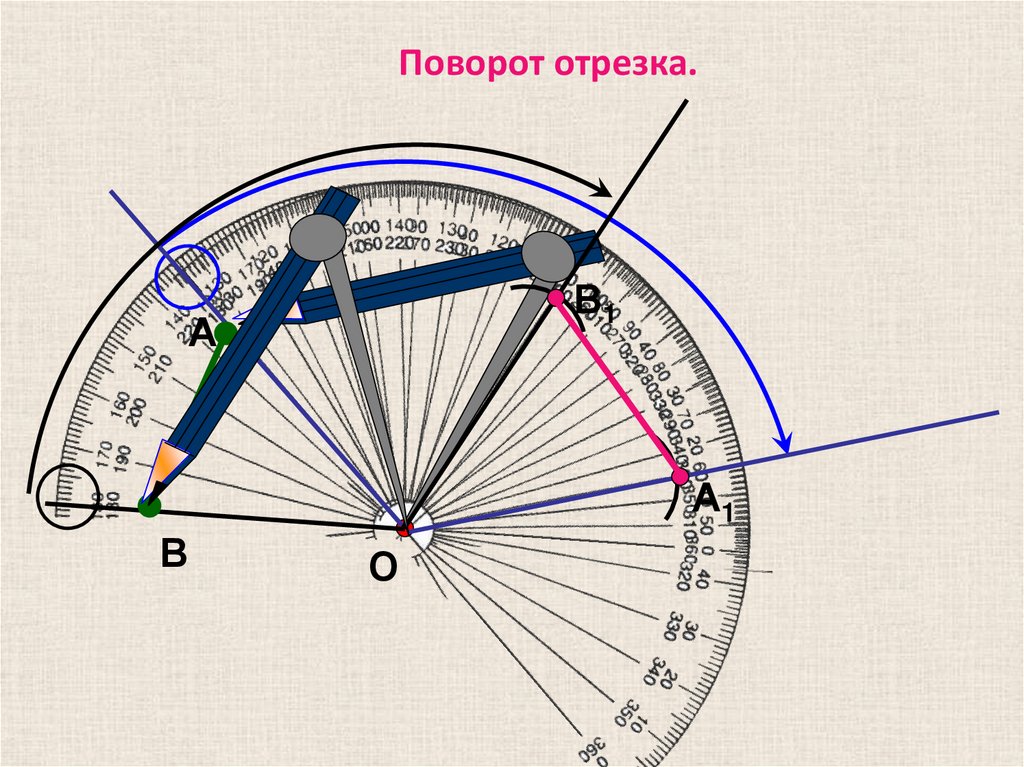
Поворот отрезка.В1
А
А1
В
О
19.
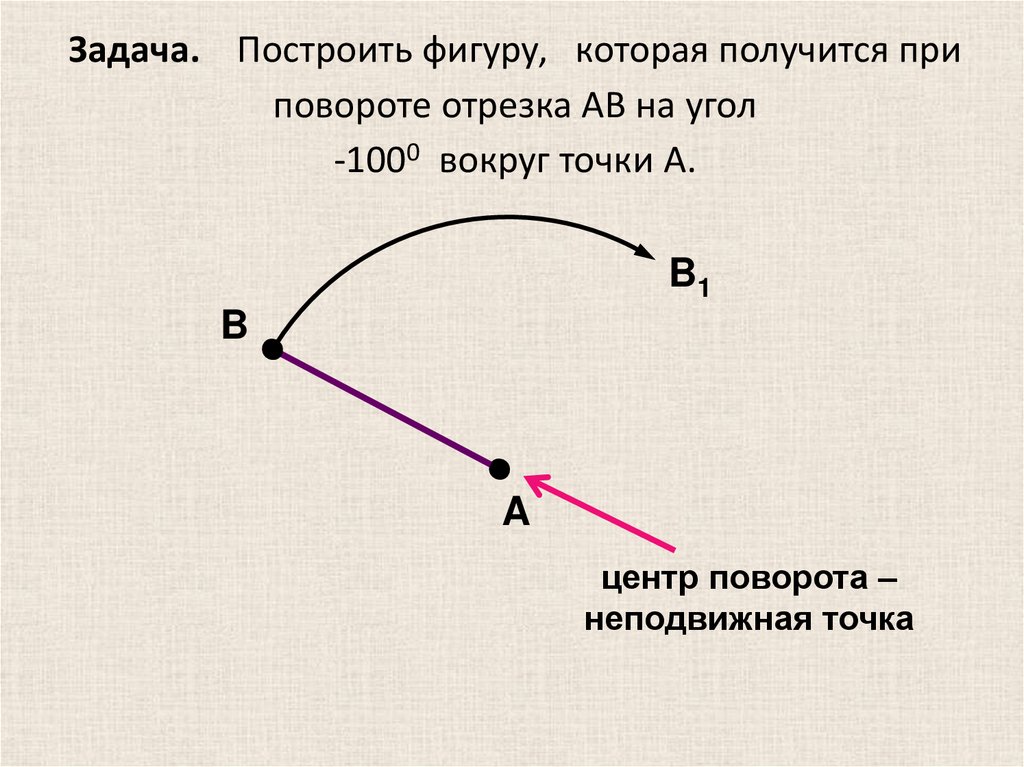
Задача. Построить фигуру, которая получится приповороте отрезка AB на угол
-1000 вокруг точки А.
B1
B
A
центр поворота –
неподвижная точка
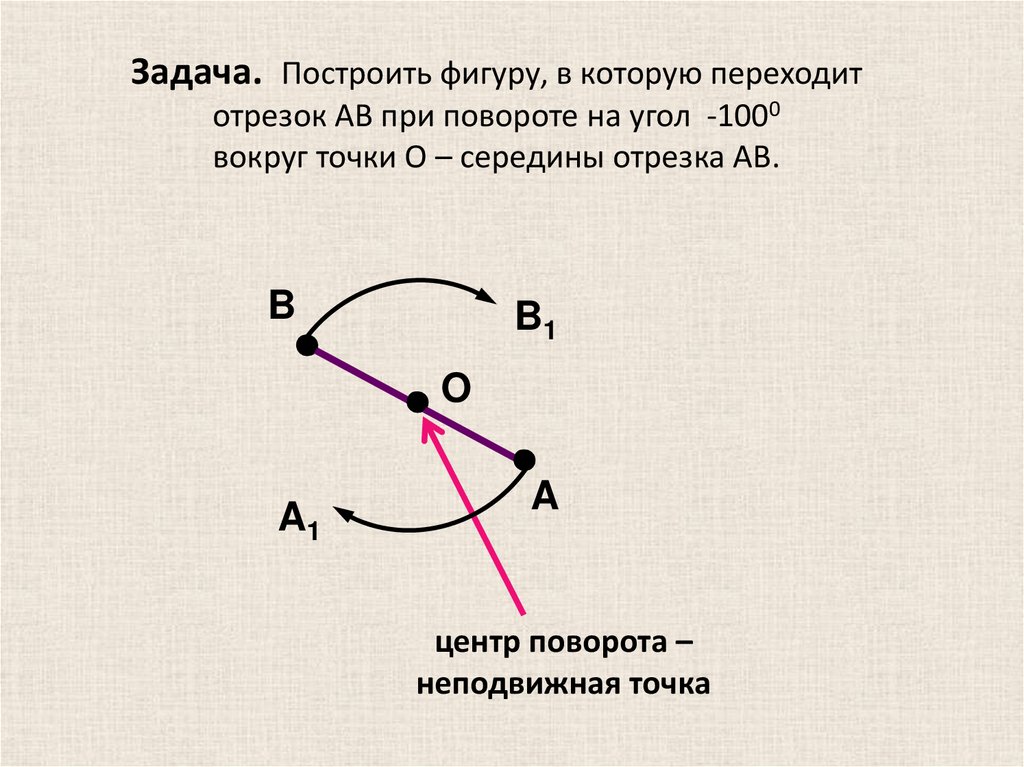
20.
Задача. Построить фигуру, в которую переходитотрезок AB при повороте на угол -1000
вокруг точки О – середины отрезка AB.
B
B1
O
A1
A
центр поворота –
неподвижная точка
21.
Центр поворота фигуры может быть вовнутренней области фигуры.
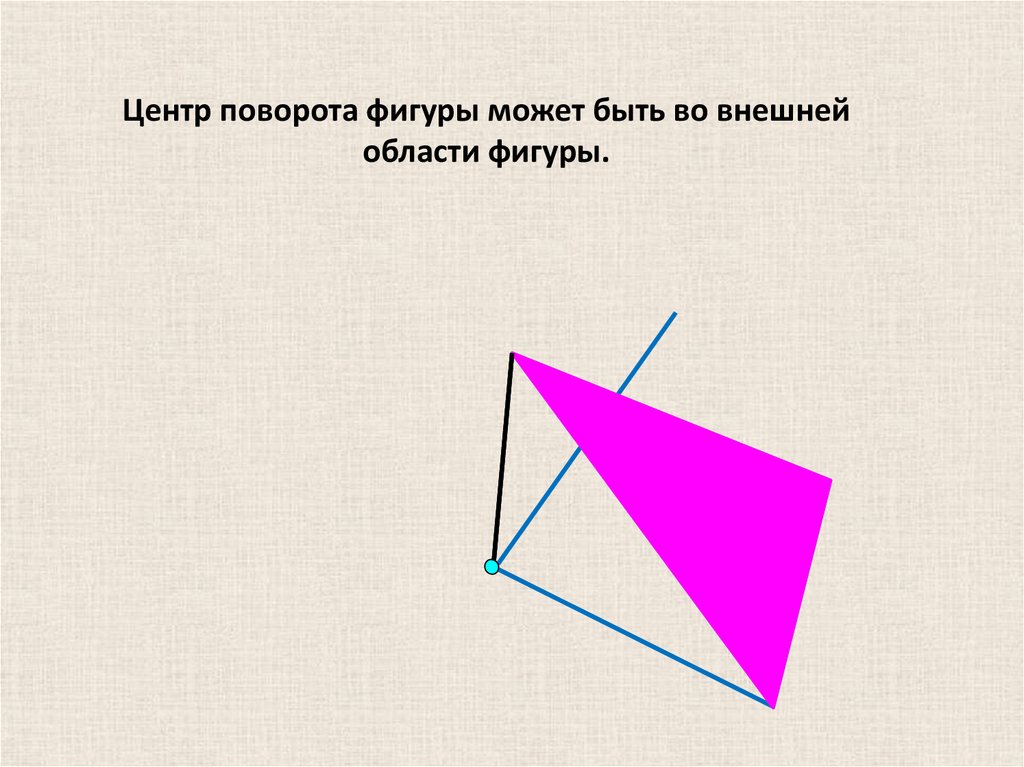
22.
Центр поворота фигуры может быть во внешнейобласти фигуры.
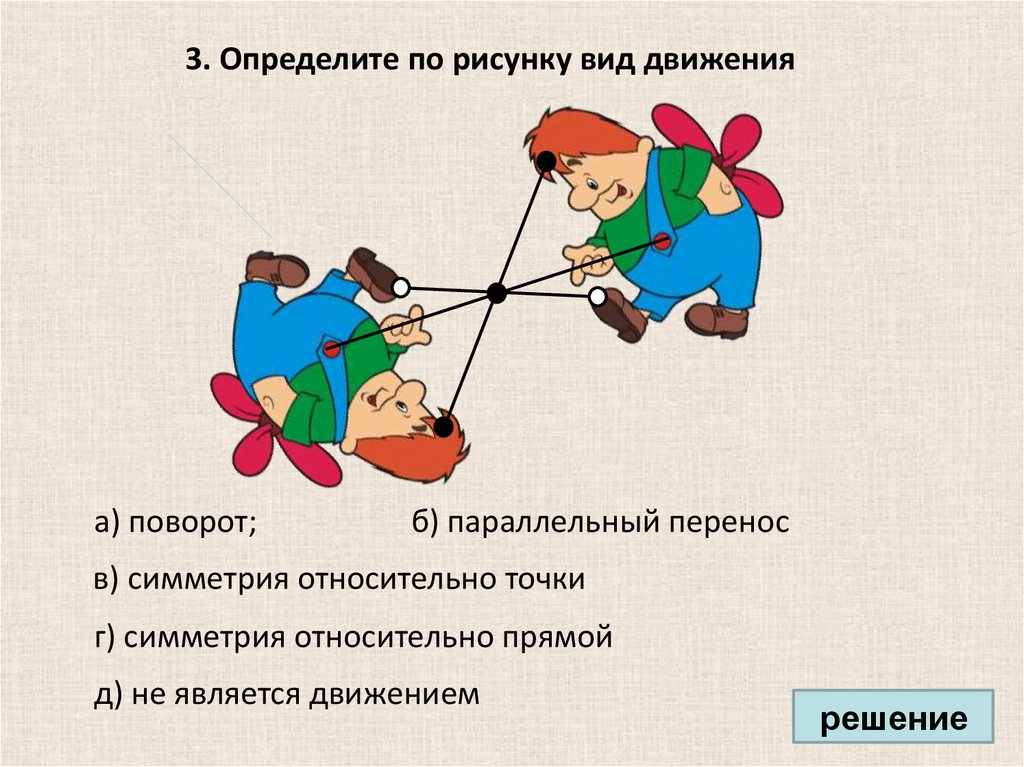
23.
1. Определите по рисунку вид движения.а) поворот
б) параллельный перенос
в) симметрия относительно точки
г) симметрия относительно прямой
д) не является движением
решение
24.
2. Определите по рисунку вид движенияа) поворот
б) параллельный перенос
в) симметрия относительно точки
г) симметрия относительно прямой
д) не является движением
решение
25.
3. Определите по рисунку вид движенияа) поворот;
б) параллельный перенос
в) симметрия относительно точки
г) симметрия относительно прямой
д) не является движением
решение
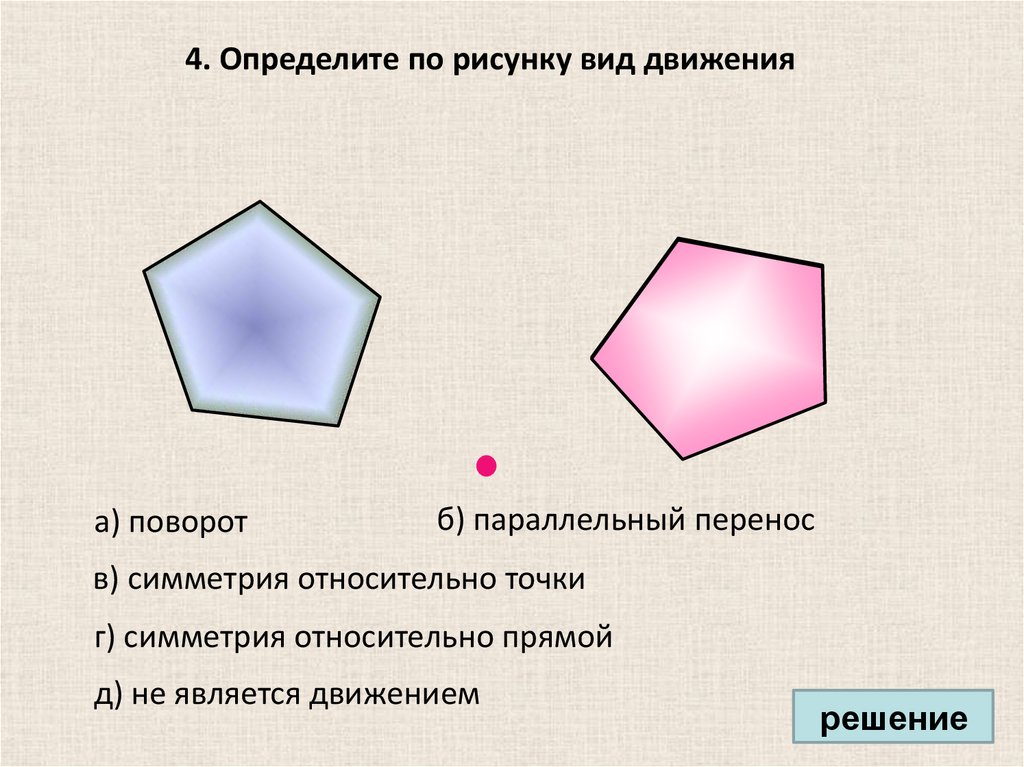
26.
4. Определите по рисунку вид движенияа) поворот
б) параллельный перенос
в) симметрия относительно точки
г) симметрия относительно прямой
д) не является движением
решение
27.
5. Определите по рисунку вид движенияа) поворот
б) параллельный перенос
в) симметрия относительно точки
г) симметрия относительно прямой
д) не является движением
решение











 mathematics
mathematics








