Координаты вектора

1. КООРДИНАТЫ ВЕКТОРА

Координатные векторы
Координаты вектора
Координаты равных векторов
Свойства координат векторов

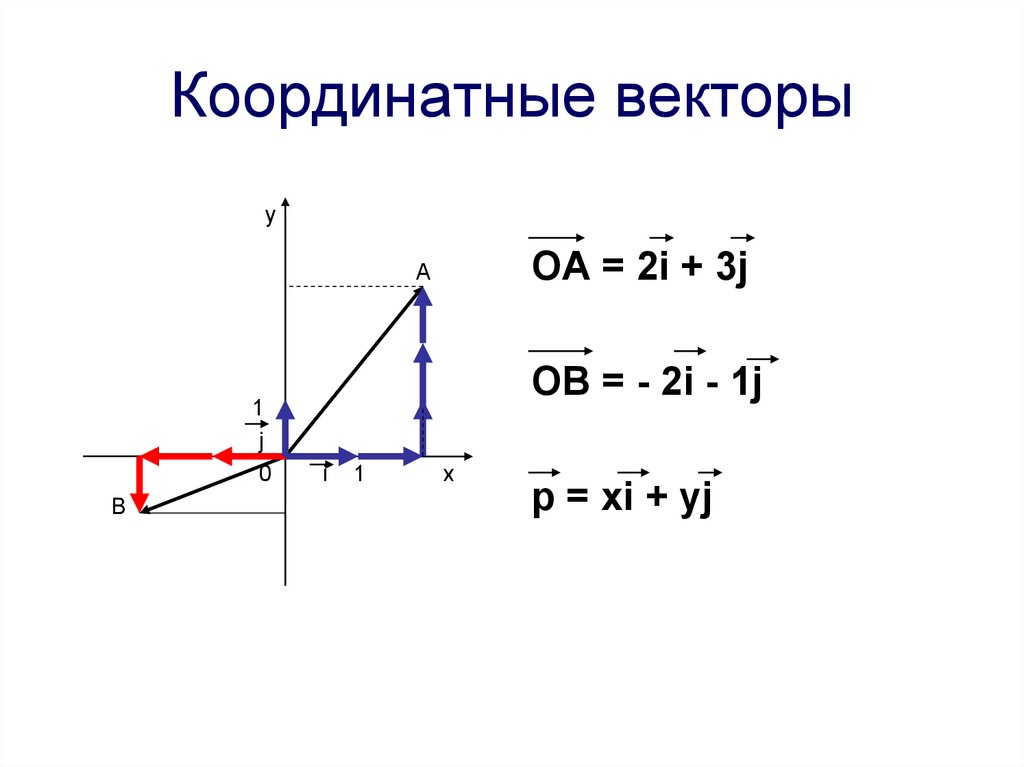
2. Координатные векторы

y
OA = 2i + 3j
A
1
j
0
B
OB = - 2i - 1j
i
1
x
p = xi + yj

3. p = xi + yj x, y – коэффициенты разложения

• Определение. Коэффициенты
разложения вектора по координатным
векторам называют координатами
вектора.
• p {x;y}
• 0 {0;0}
• OA {2;3}
• OB {-2; -1}

4. Координаты равных векторов

Если a = x1i + y1j
и b = x2i + y2j равны, то
x1 = x2 и y1 = y2.
Координаты равных векторов равны.

5. Свойства координат векторов

Пример:
a {-3;4}
b {-2;-1}
Ответы:
Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
m {x1 ;y1 }; n {x2;y2} m + n {x1 + x2;y1 + y2}
a+b
{-5;3}
Каждая координата разности двух или
более векторов равна разности
соответствующих координат этих векторов.
m {x1 ;y1 }; n {x2;y2} m - n {x1 - x2;y1 - y2}
a–b
{-1;5}
Каждая координата произведения вектора
на число равна произведению
соответствующей координаты вектора на
это число. m {x1 ;y1 }; a∙m {a ∙ x1 ; a ∙ y1 }
3a
-0,5b
{-9;12}
{1;0,5}
Свойство: