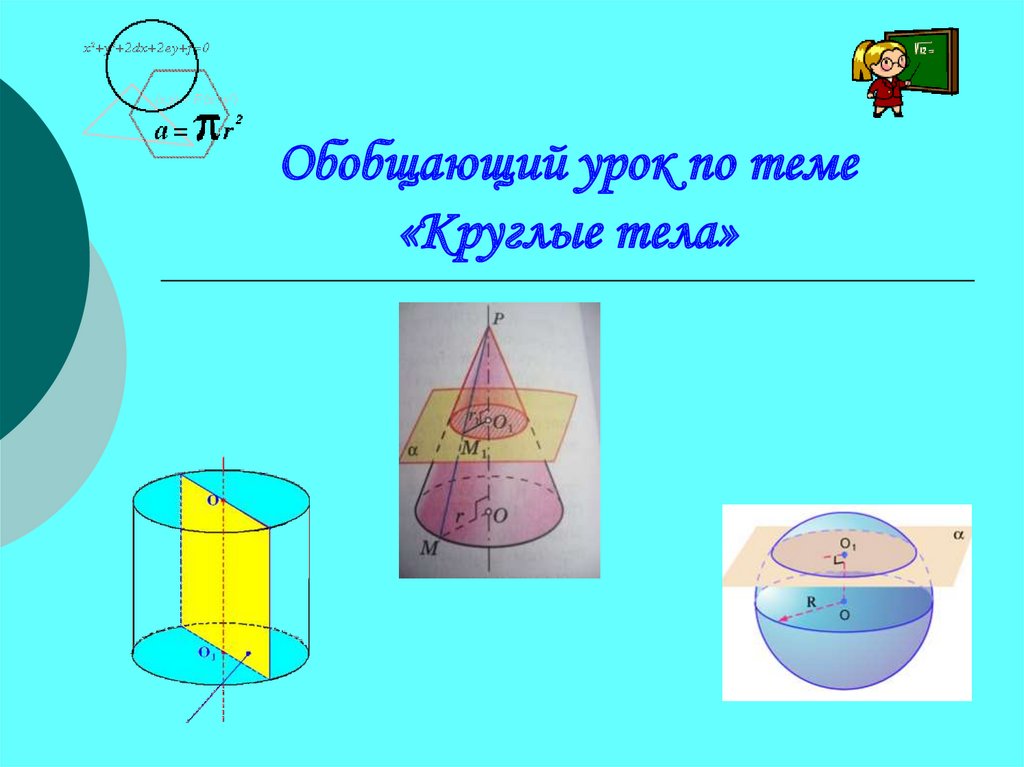
Обобщающий урок по теме «Круглые тела»

1. Обобщающий урок по теме «Круглые тела»

2.

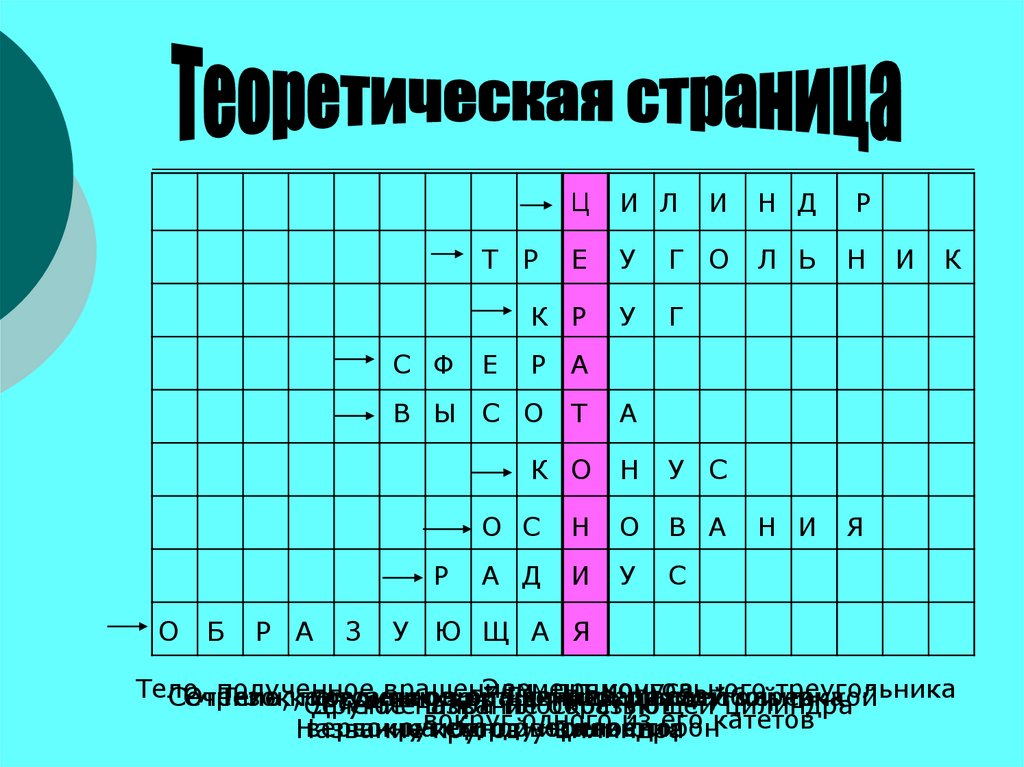
Ц
И Л
И
Н Д
Р
Е
У
Г
О
Л Ь
Н
К Р
У
Г
Н И
Я
Т Р
С Ф
Е
О
Б
Р А
З
У
К
Р А
В Ы С О
Р
И
Т
А
К О
Н
У С
О С
Н
О
В А
А Д
И
У
С
Ю Щ А Я
Элемент
конуса
Тело,
полученное
вращением
прямоугольного
треугольника
Граница
шара
Сечение
Отрезок,
Тело,конуса
полученное
соединяющий
плоскостью,
вращением
центр
проходящей
шара
прямоугольника
с любой
через
точкой
Сечение
Другое
название
шара
плоскостью
образующей
цилиндра
вокруг
одного
его катетов
вершину
вокруг
на
и
его
одной
хорду
поверхности
основания
егоиз
сторон
Название
кругов
уиз
цилиндра

3.

Вечнозелёное дерево, достигающее
десятиметровой высоты. Внешним видом
оно напоминает белую акацию. Плоды
этого растения – стручки, размеры
которых от 10 до 25 см в длину. Одно
дерево дает за год до 200 кг плодов.
Семена находятся в сочной и сладкой
мякоти стручков и обладают интересной
особенностью: у всех семян одинаковый
вес – 200мг.
В давние времена ювелиры и аптекари
применяли их как своеобразные гири
для взвешивания драгоценных камней и
благородных металлов, порошков и
пилюль.
От греческого «цератония» происходит
и название единицы массы драгоценных
камней - карат

4.

5.

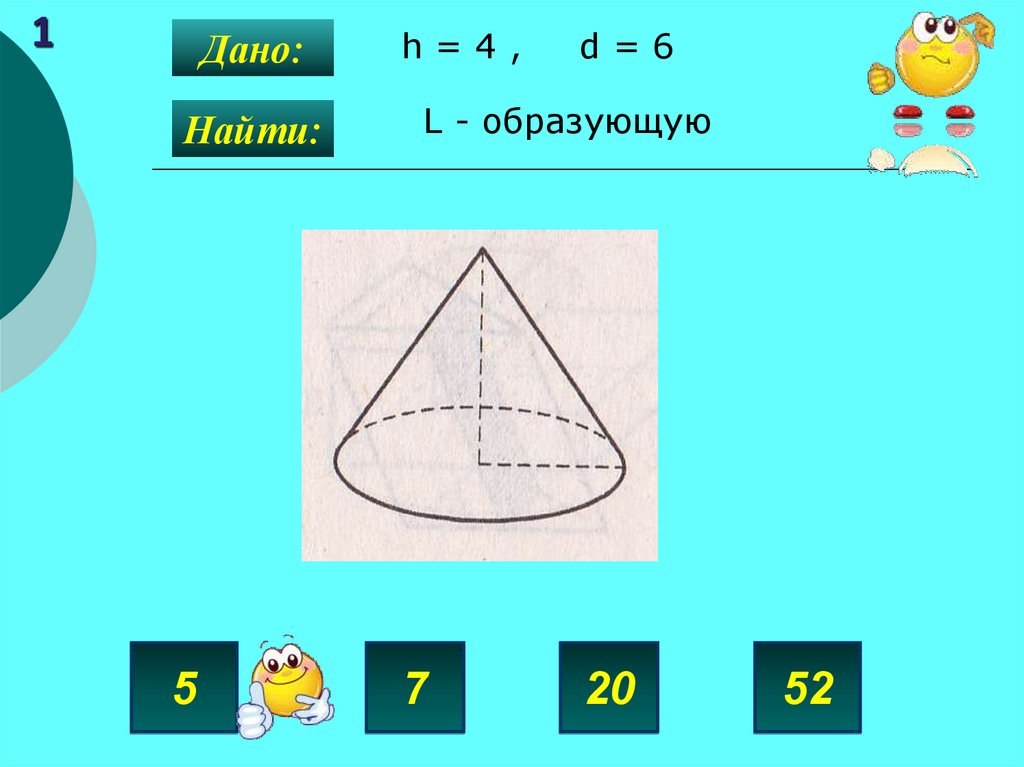
1
Дано:
Найти:
5
h=4,
d=6
L - образующую
7
20
52

6.

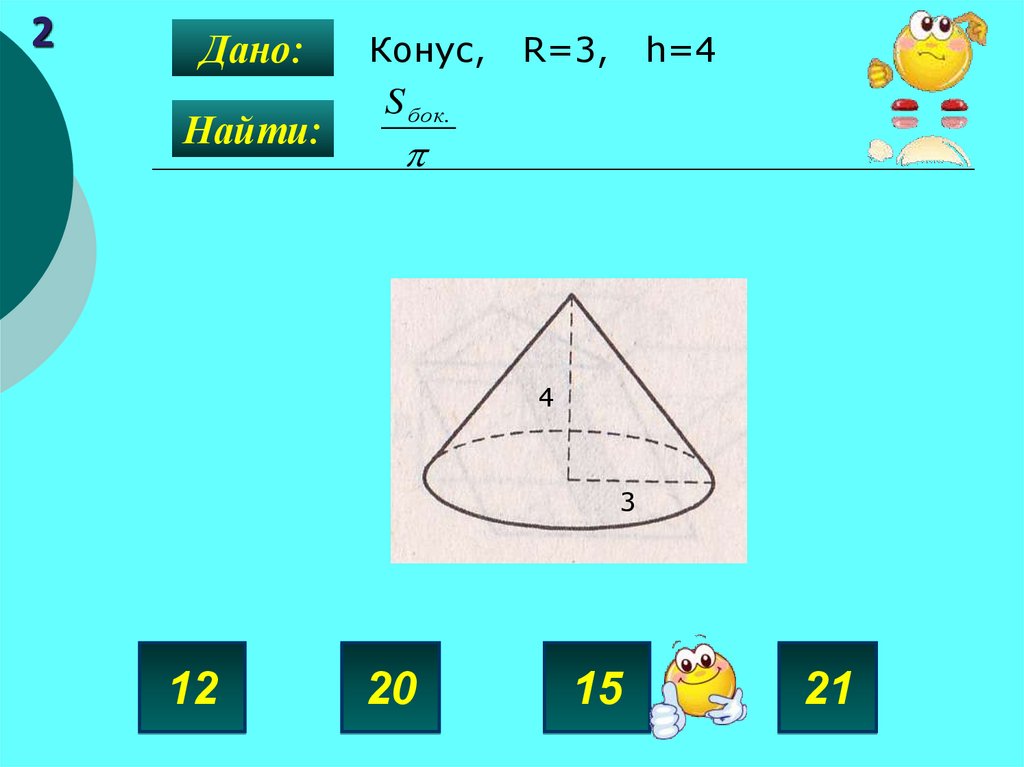
2
Дано:
Найти:
Конус,
R=3,
h=4
S бок.
4
3
12
20
15
21

7.

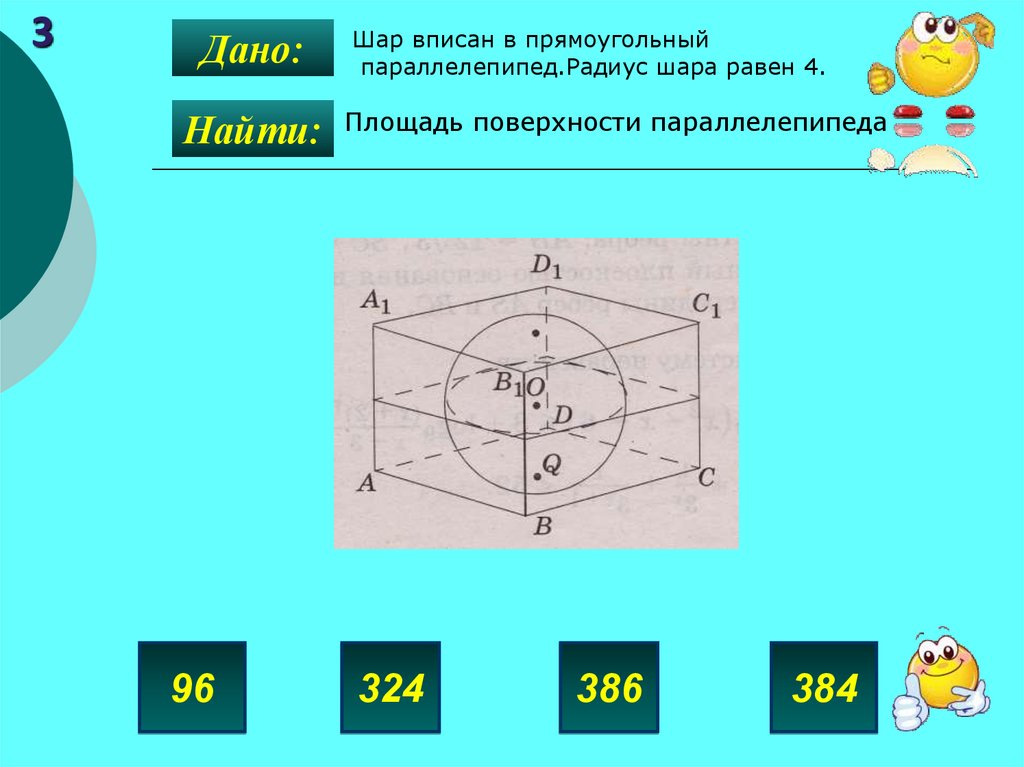
3
Дано:
Найти:
96
Шар вписан в прямоугольный
параллелепипед.Радиус шара равен 4.
Площадь поверхности параллелепипеда
324
386
384

8.

4
Дано:
Найти:
Площадь поверхности шара равна 20.
Площадь большого круга
5
10
R
4
2

9.

5
( x 1) 2 y 2 ( z 7) 2 28
Дано:
Найти:
А БВГ-
А
Найти координаты центра
и радиус сферы
С(1; 0; -7) ,
R 7 2
С(-1; 0; 7) ,
R 2 7
С(-1; 0; 7) ,
С(1; 0; 7) ,
Б
R 7 2
R 2 7
В
Г

10.

Решаем задачи
заполняем таблицу,
читаем слово.

11.

Проверяем 1
Дано уравнение сферы. Найдите
координаты центра и радиус этой сферы
( x 1) ( y 5) ( z 3) 18
2
2
2
В-
С(-1; 5; -3),
R=
3 2
A-
С(-1; 5; -3),
R=
2 3
Г-
С(1; -5; 3),
R=
3 2
Ю-
С(1; -5; 3),
R =2
1
Г
2
3
4
5
3
6
7
8

12.

Проверяем 2
Дана точка С(0; 3; -2) – центр сферы, радиус R 2=
Найдите ниже уравнение этой сферы.
2
2
2
x
(
y
3
)
(
z
2
)
50
К-
А-
x 2 ( y 3) 2 ( z 2) 2 20
Б-
x 2 ( y 3) 2 ( z 2) 2 50
И-
x 2 ( y 3) 2 ( z 2) 2 20
1
2
Г А
3
4
5
6
7
8
5
.

13.

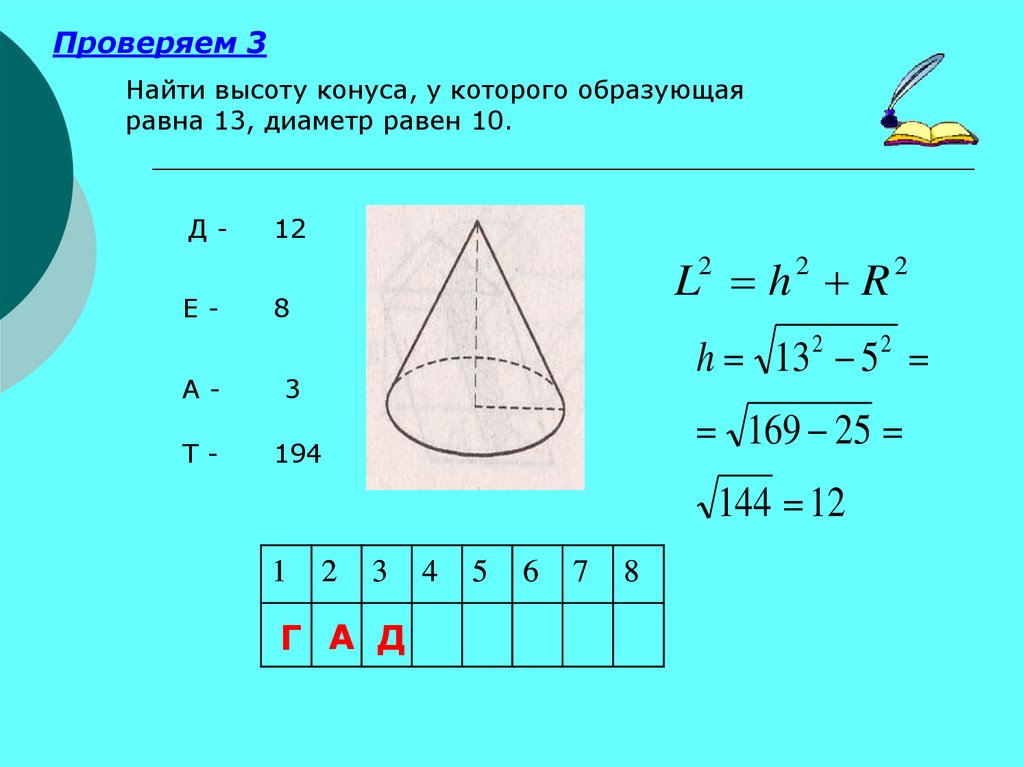
Проверяем 3
Найти высоту конуса, у которого образующая
равна 13, диаметр равен 10.
ДЕ-
12
L2 h 2 R 2
8
h 13 5
2
А-
3
Т-
194
169 25
144 12
1
2
2
3
Г А Д
4
5
6
7
8

14.

Проверяем 4
Найти площадь полной поверхности цилиндра, у которого
Высота в 3 раза больше радиуса, равного 5.
S
В ответе запишите
А-
300
S п 2 R(h R) 2 5(15 5) 200
Т - 150
В ответе:
Е З -
100
200
1
2
3
4
Г А Д З
5
6
7
8
200
200

15.

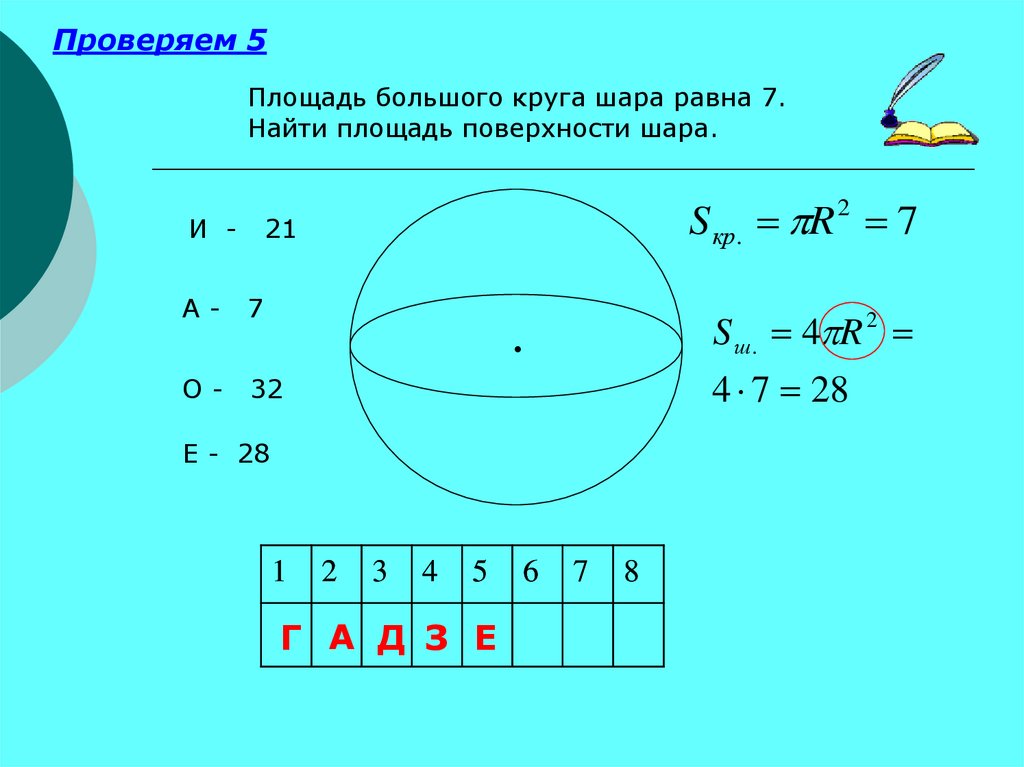
Проверяем 5
Площадь большого круга шара равна 7.
Найти площадь поверхности шара.
И А-
S кр . R 2 7
21
7
S ш. 4 R 2
О-
4 7 28
32
Е - 28
1
2
3
4
5
Г А Д З Е
6
7
8

16.

Проверяем 6
Площадь поверхности шара
Найти диаметр шара.
196
.
4 R 196
2
R 49
2
Р-7
Т - 14
R 7
А - 16
d 14
С - 3,5
1
2
3
4
5
6
Г А Д З Е Т
7
8

17.

Проверяем 7
Длина окружности основания цилиндра С = 0,2,
высота равна 50. Найти площадь боковой
поверхности цилиндра.
С 2 R 0,2
Т - 10
М- 5
S бок. 2 Rh
И - 100
0,2 50 10
Е - 50
1
2
3
4
5
6
7
Г А Д З Е Т Т
8

18.

Проверяем 8
Радиусы двух шаров равны 2 6 и 5. Найти радиус
шара, площадь которого равна сумме площадей
двух данных шаров.
4 R32 4 R12 4 R22
Ь - 49
R32 R12 R22
Е - 14
R32 24 25 49
А- 7
R=7
У - 6,5
1
2
3
4
5
6
7
8
Г А Д З Е Т Т А
: 4

19.

ГАДЗЕТТА (итал. gazzetta) — народное
название чеканенных с 1539 г.
венецианских биллонных монет в 2
сольдо. Выпускались номиналы в 2, 3,
4 и 10 гадзетта.
За одну такую монету житель
Венецианской республики мог купить
рукописный листок, в котором
сообщались новости.
(отсюда происходит современное
слово - газета).

20.

Математику уже затем учить надо,
что она ум в порядок приводит.
(М.В. Ломоносов)