Теорема Пифагора

1. Теорема Пифагора

Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век

2. Цели урока

Изучим теорему Пифагора и
познакомимся с
историческими сведениями,
связанными с этой теоремой,
рассмотрим её применение
при решении задач.

3. Актуализация опорных знаний

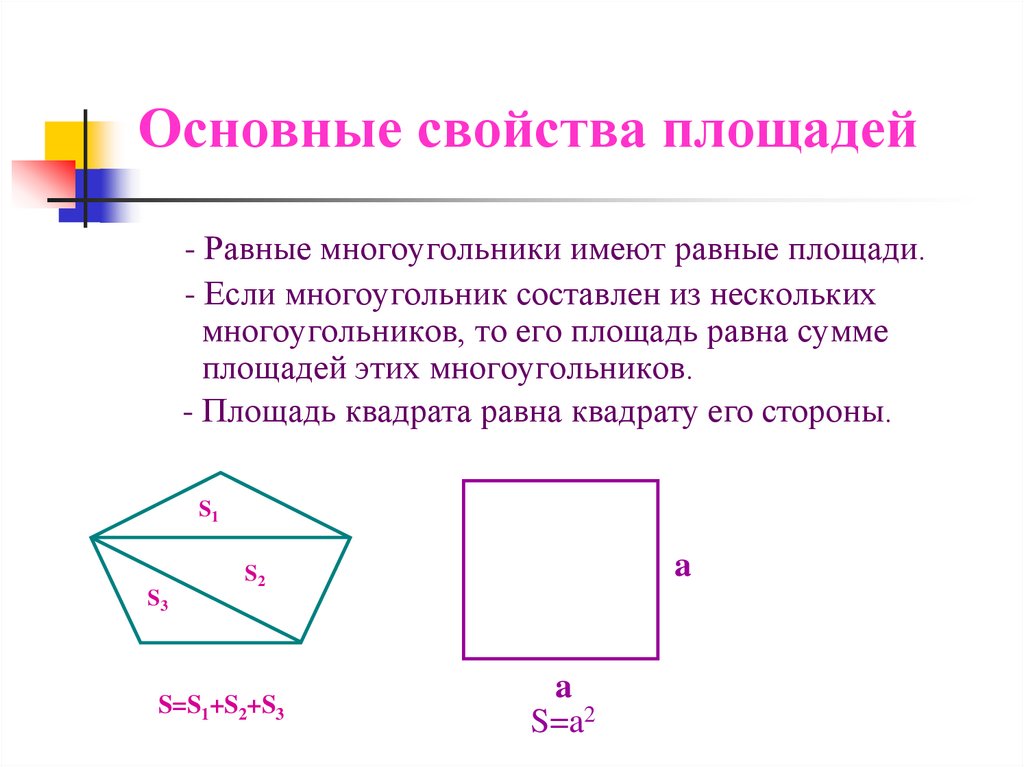
4. Основные свойства площадей

- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких
многоугольников, то его площадь равна сумме
площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны.
S1
a
S2
S3
S=S1+S2+S3
a
S=a2

5. Площадь прямоугольника

B
C
b
A
S ab
a
D
Площадь
прямоугольника
равна произведению
его смежных сторон
S a b

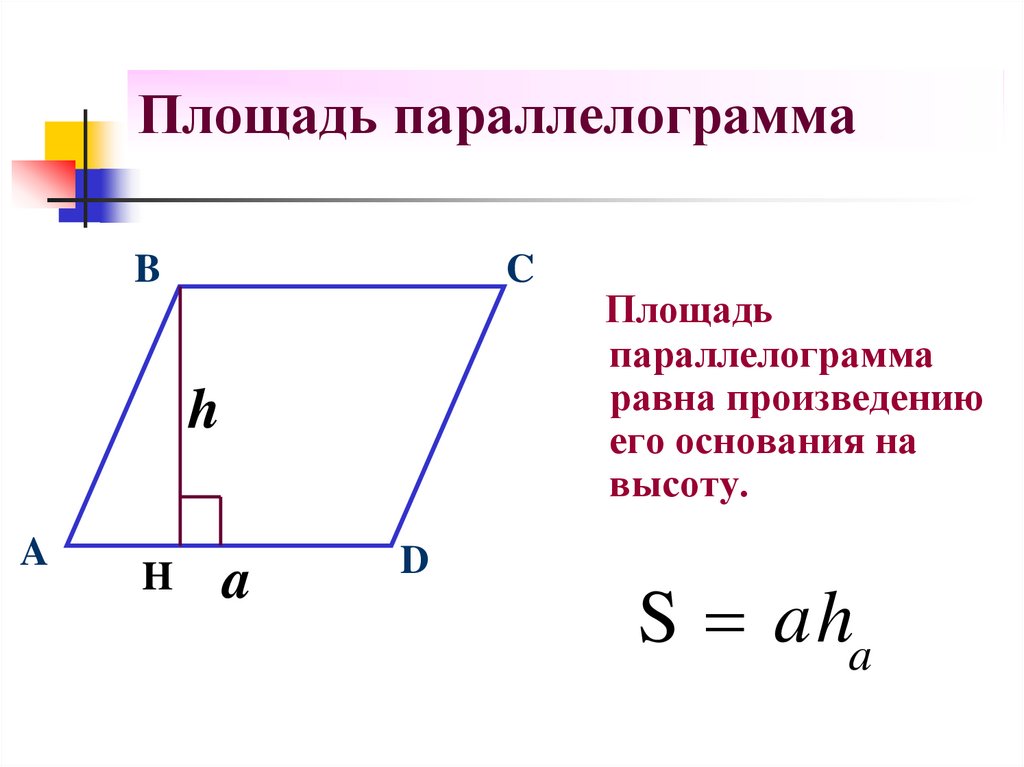
6. Площадь параллелограмма

B
C
h
A
H
a
D
Площадь
параллелограмма
равна произведению
его основания на
высоту.
S aha

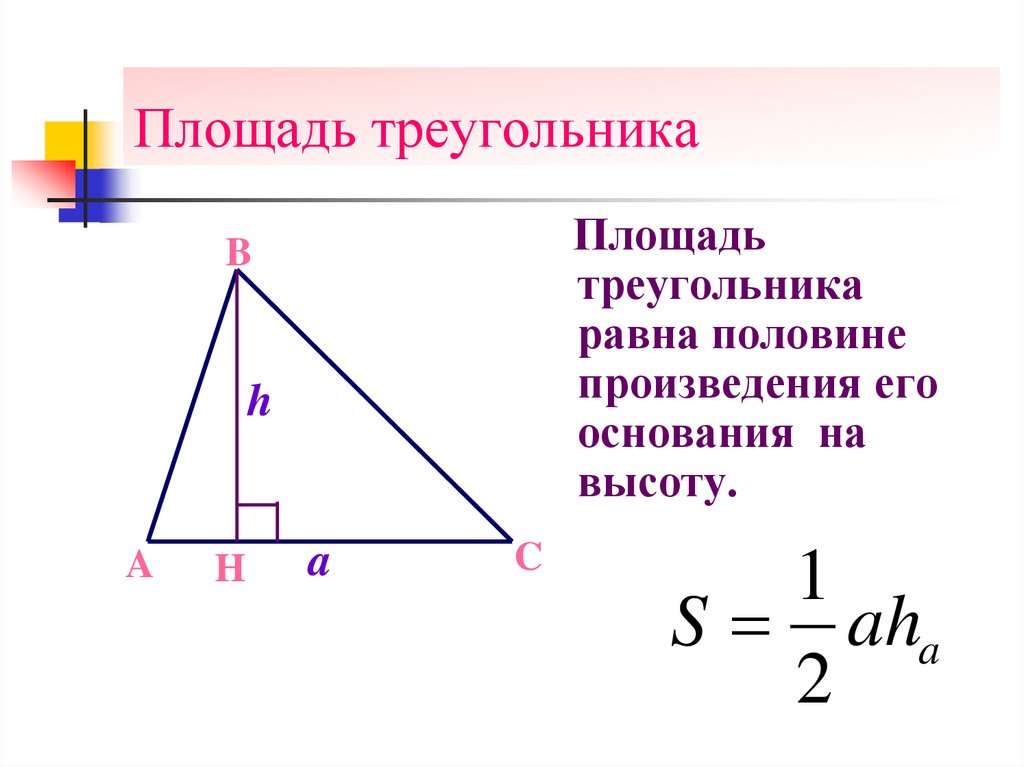
7. Площадь треугольника

Площадь
треугольника
равна половине
произведения его
основания на
высоту.
B
h
A
H
a
C
1
S aha
2

8. Площадь треугольника

Следствие 1. Площадь прямоугольного треугольника
равна половине произведения его катетов.
Следствие 2. Если высоты двух треугольников равны,
то их площади относятся как основания.

9. Решение задач по готовым чертежам

Подготовка к восприятию нового материала

10. 1. Найдите площадь четырёхугольника ABCD

В
6
A
8
30
C
45
D
Ответ: 96см
2

11. 2. Найдите угол β.

α
β
γ
Ответ: β = 180 - (α + γ)

12. 3. Докажите, что MNPK - квадрат

N
B
2
4
C
3
1
P
M
A
K
D

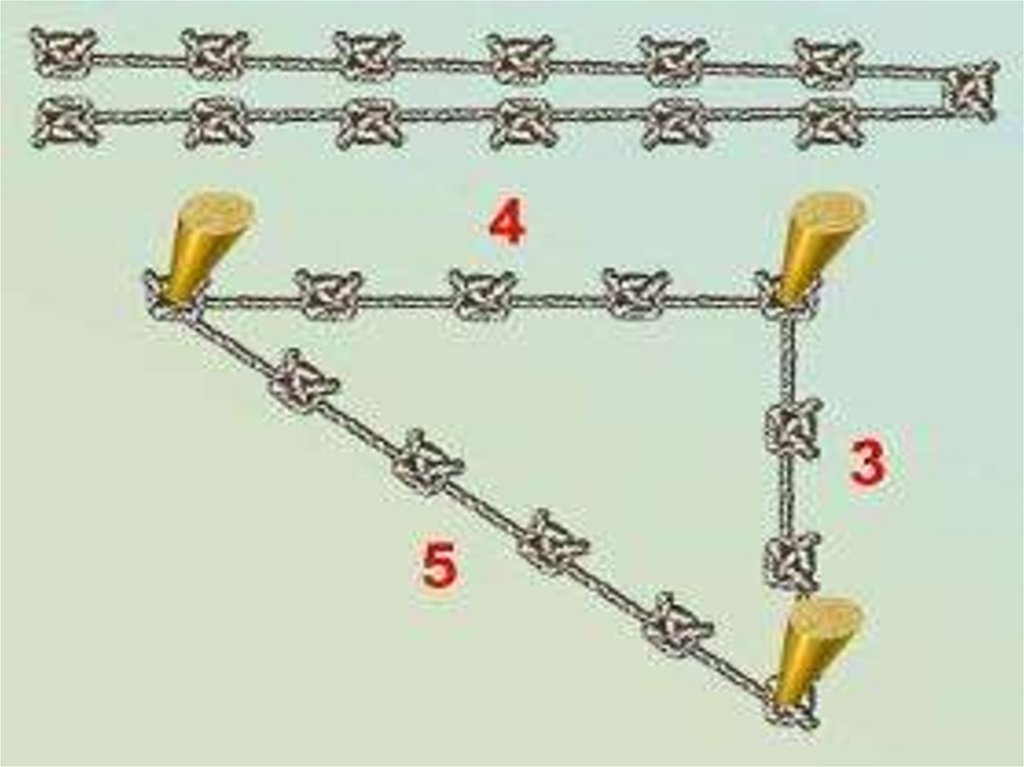
13. Исторический телетайп

14.

15.

16.

17.

18.

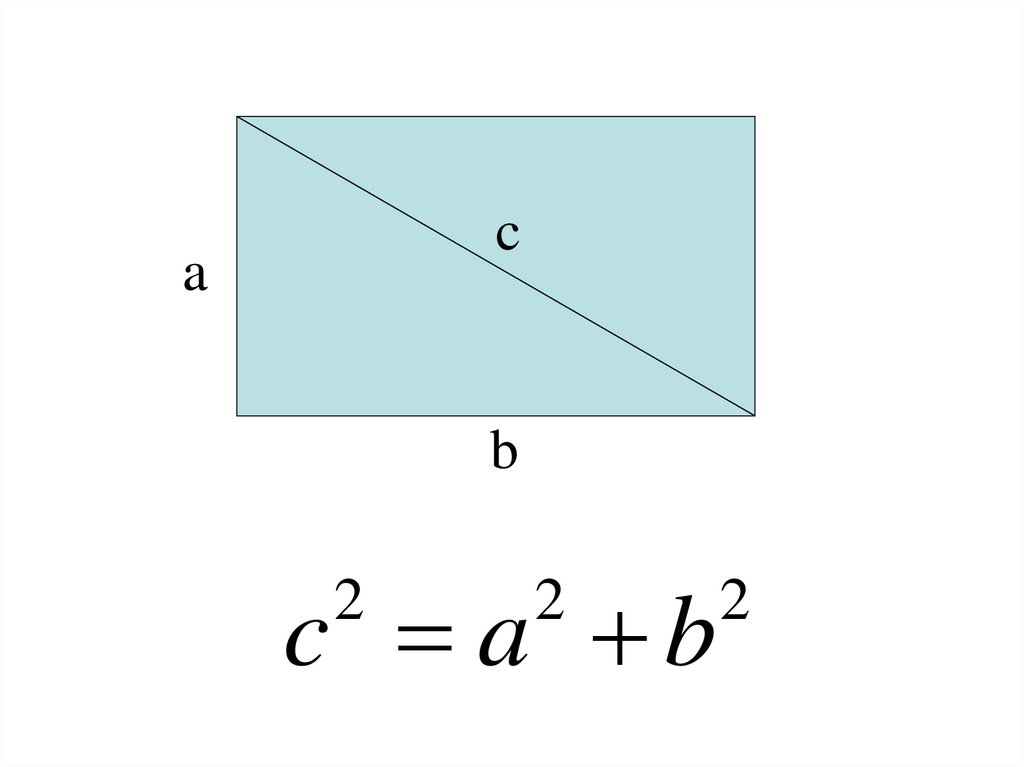
c
a
b
c a b
2
2
2

19.

c a b
2
2
2

20.

c a b
2
2
2

21.

22.

23.

24. Изучение нового материала

Хотя эта теорема и древняя, но и сегодня
наши современники пытаются слагать о
ней стихи.
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда найдем.
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путем
К результату мы придем.

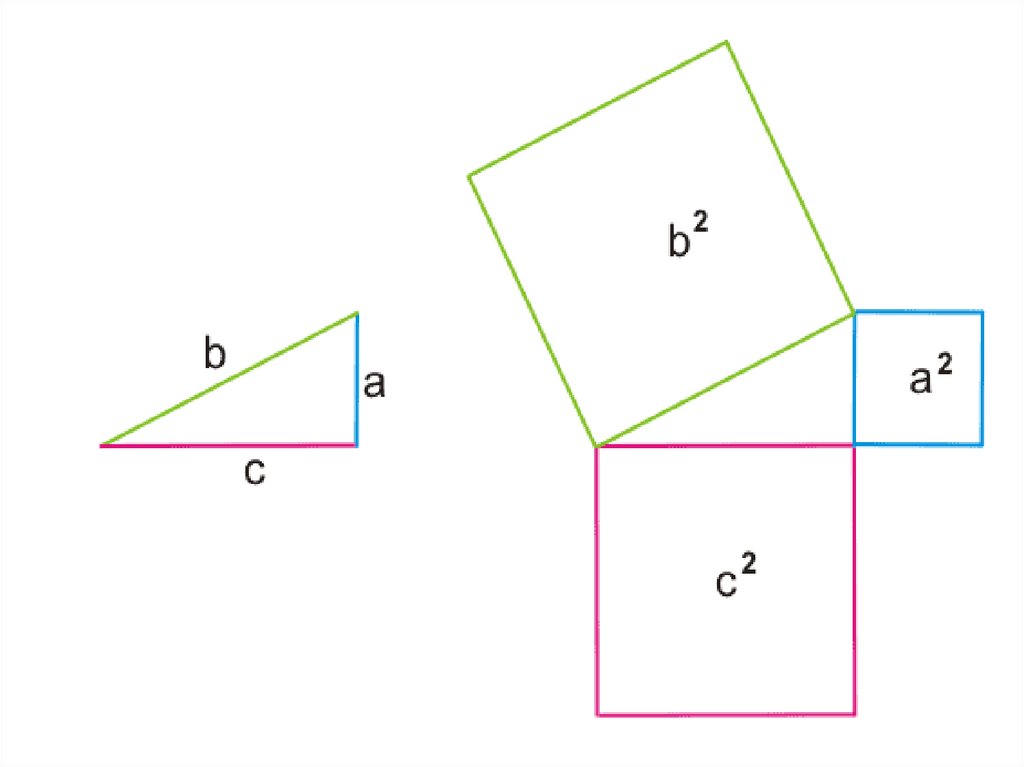
25.

В прямоугольном треугольнике
квадрат гипотенузы равен сумме
квадратов его катетов.

26.

b
Дано:
a
c
прямоугольный
треугольник,
а и b – катеты,
с – гипотенуза
Доказать: c a b
2
2
2

27.

a
b
a
b
c
c
S
c
c
b
a
b
a

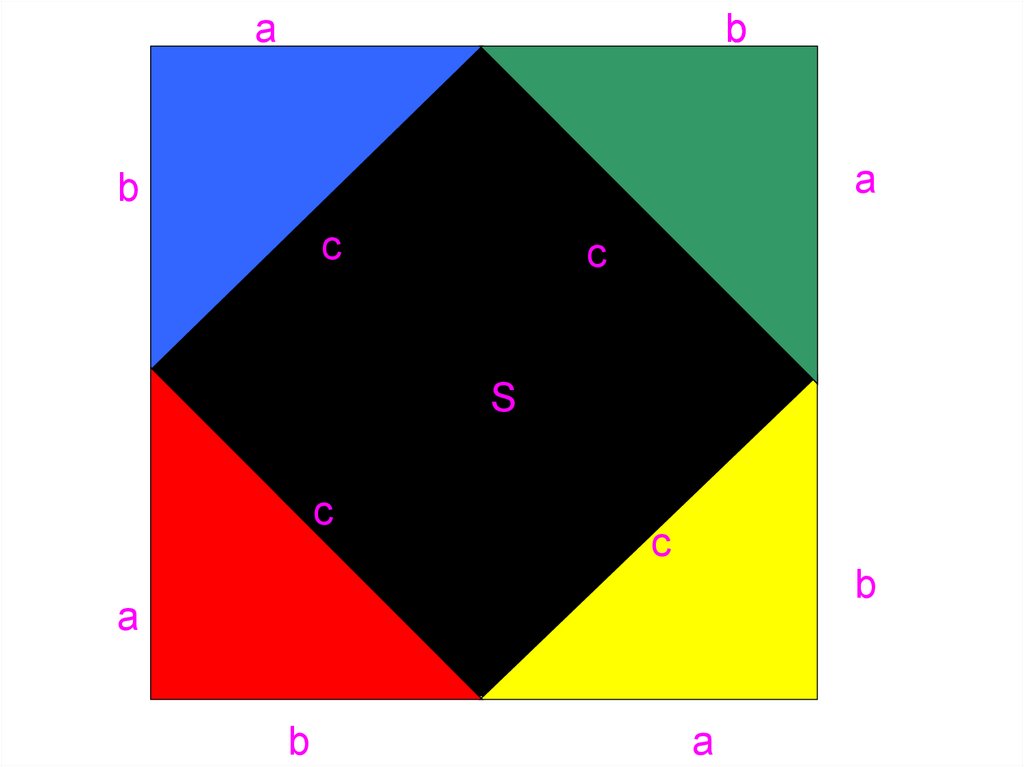
28.

a
b
b
c
c
a
S
c
c
b
a
b
a
c a b
2
2
2

29. Закрепление изученного материала

Решить устно № 483 (а), № 484 (а).
Решить на доске и в тетрадях задачу № 487.
Дополнительно:
1.
2.
3.
В
В
5 см
A
12 см
6 см
А
?
Н
В
?
?
7 см
С
А
5 см
С
С

30. Практическая работа

Задание
для первого
ряда
Построить
треугольник по
трём сторонам
7 см , 3 см, 8 см.
Измерить
транспортиром
угол, лежащий
против большей
стороны.
Задание
для второго
ряда
Построить
треугольник по
трём сторонам
4см , 3 см, 5 см.
Измерить
транспортиром
угол, лежащий
против большей
стороны.
Задание
для третьего
ряда
Построить
треугольник по
трём сторонам
6 см , 8 см, 10 см.
Измерить
транспортиром
угол, лежащий
против большей
стороны.

31. Задание на дом:

П. 54, вопрос 8.
2. № 483 (в, г), 484 (в, г), 486 (в).
1.