Применение теорем синусов и косинусов для решения треугольников

1.

Урок № 36.

2.

Часто знает и дошкольник,
Что такое треугольник.
А уж вам-то как не знать.
Но совсем другое дело –
Очень быстро и умело
Треугольники «решать».

3. Станция «Теоретическая»

4.

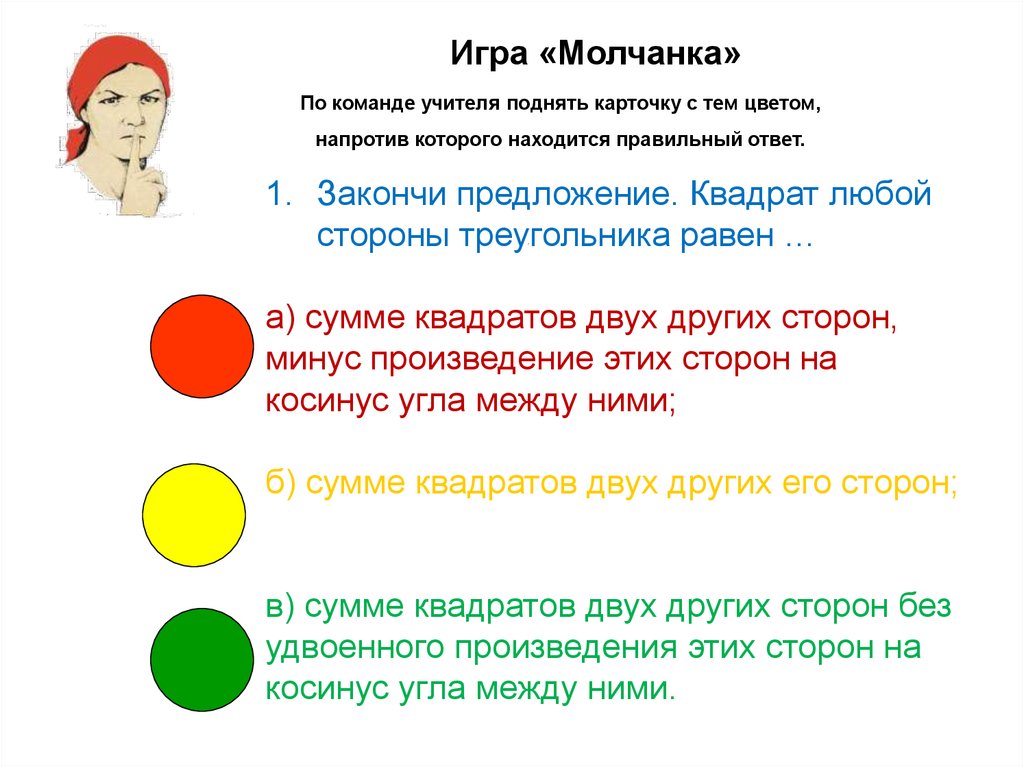
Игра «Молчанка»
По команде учителя поднять карточку с тем цветом,
напротив которого находится правильный ответ.
1. Закончи предложение. Квадрат любой
стороны треугольника равен …
а) сумме квадратов двух других сторон,
минус произведение этих сторон на
косинус угла между ними;
б) сумме квадратов двух других его сторон;
в) сумме квадратов двух других сторон без
удвоенного произведения этих сторон на
косинус угла между ними.

5.

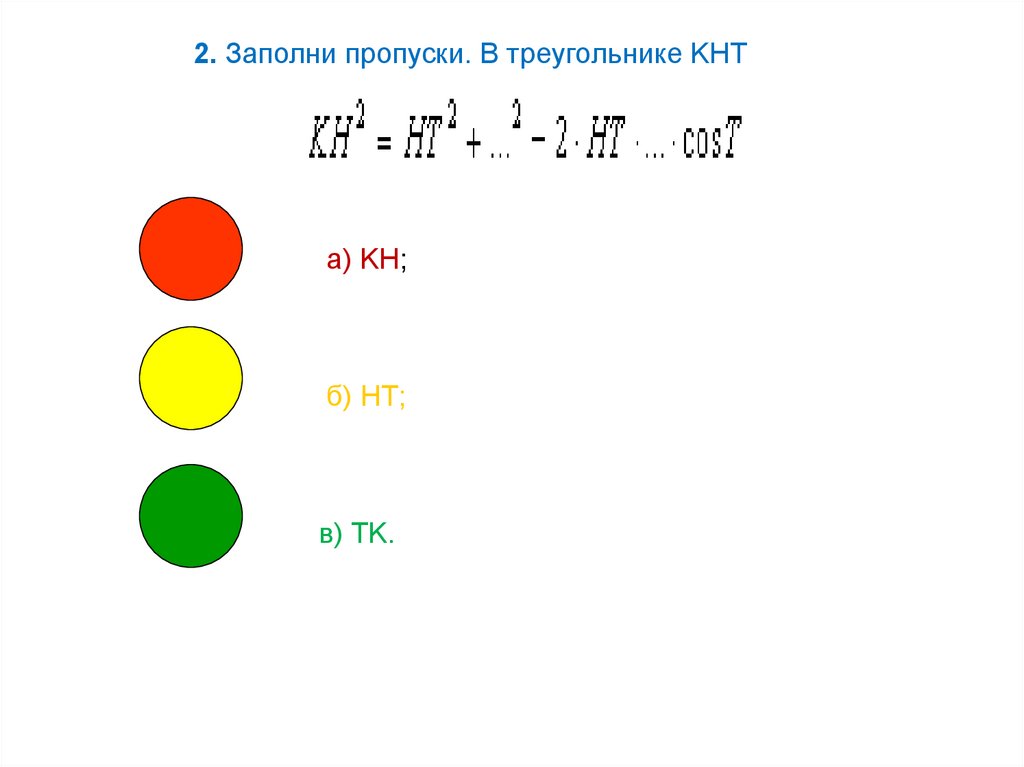
2. Заполни пропуски. В треугольнике KHT
а) KH;
б) HT;
в) TK.

6.

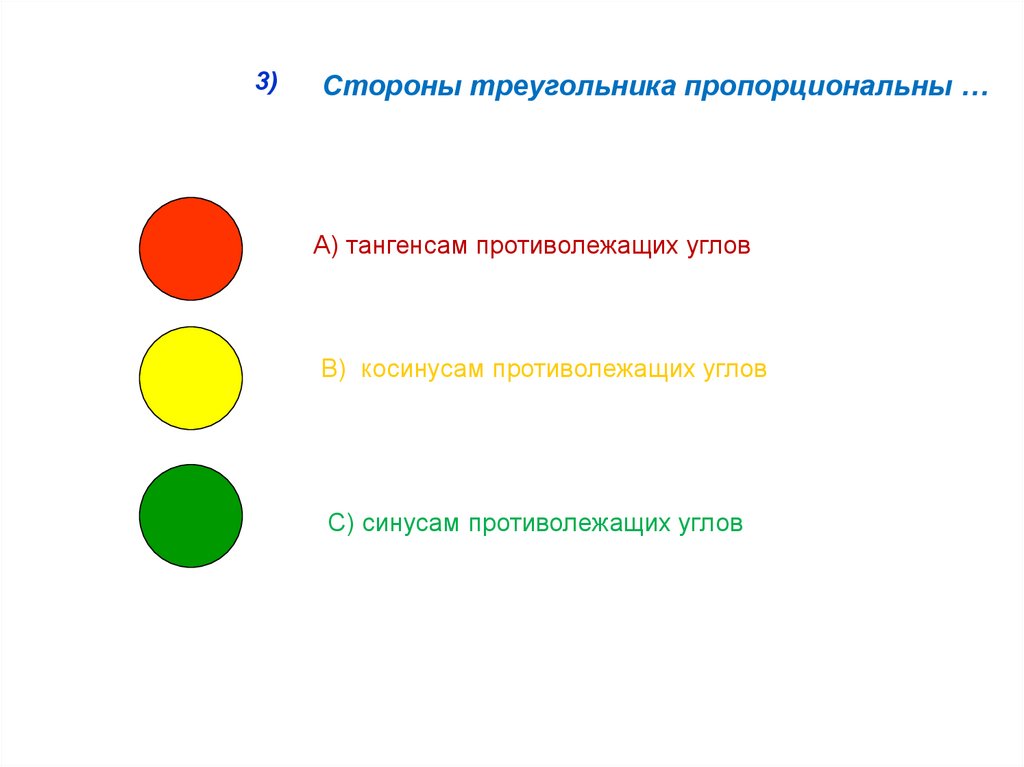
3)
Стороны треугольника пропорциональны …
А) тангенсам противолежащих углов
В) косинусам противолежащих углов
С) синусам противолежащих углов

7.

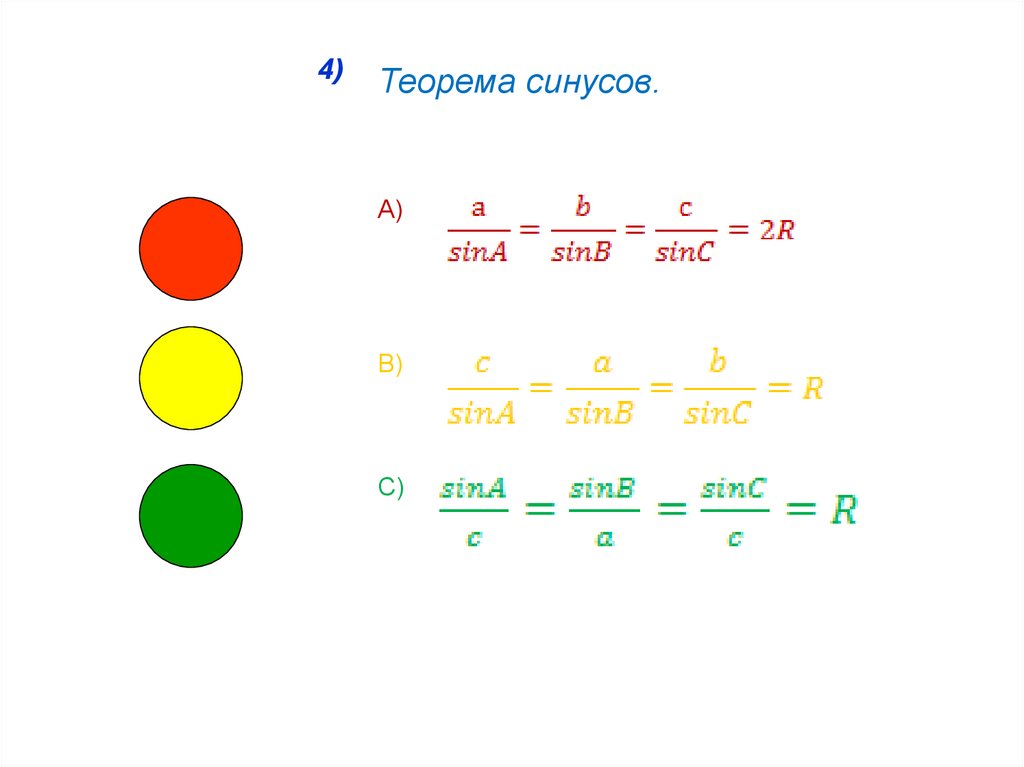
4)
Теорема синусов.
А)
В)
С)

8.

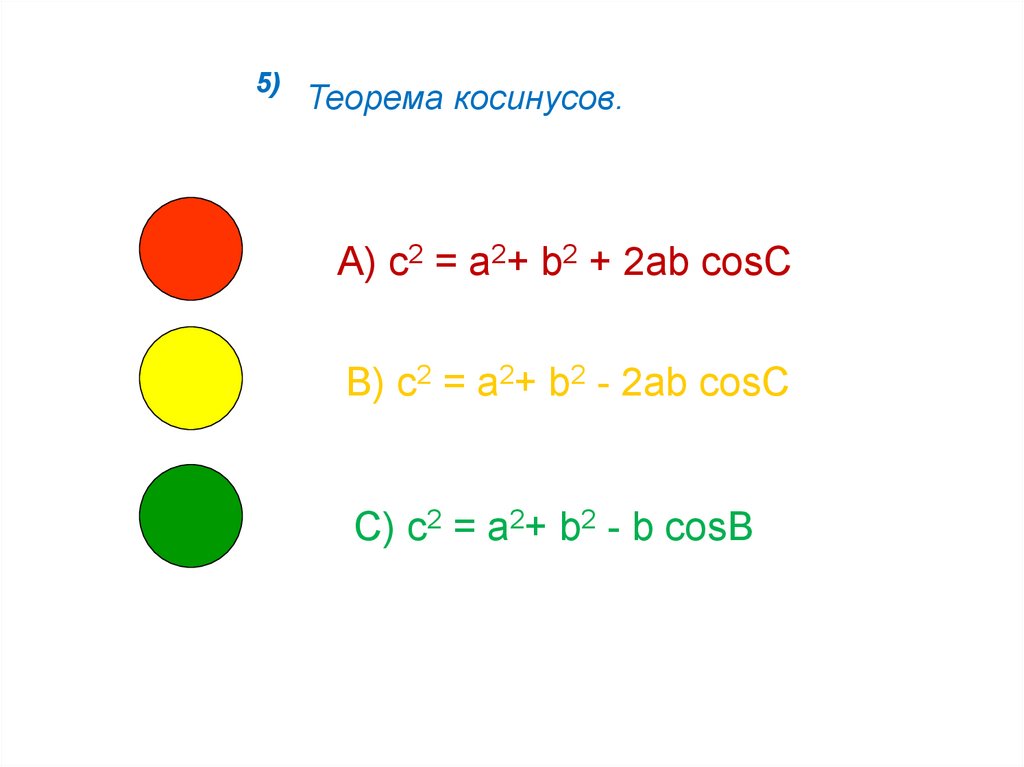
5)
Теорема косинусов.
А) с2 = a2+ b2 + 2ab cosC
В) с2 = a2+ b2 - 2ab cosC
С) с2 = a2+ b2 - b cosB

9.

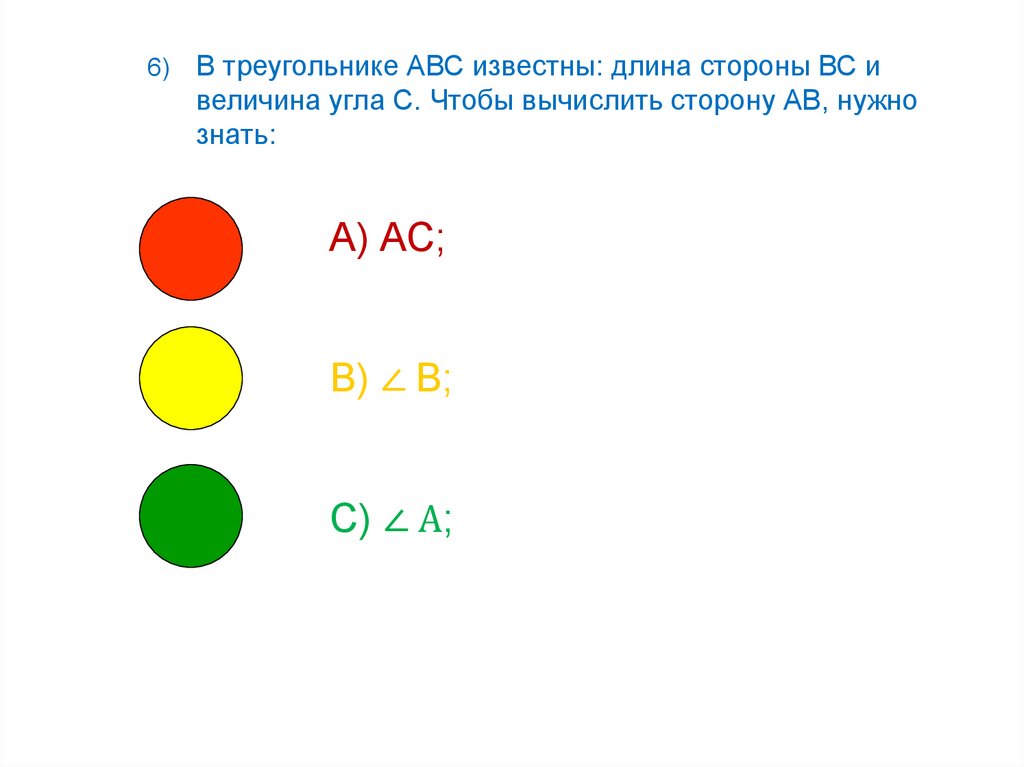
6)
В треугольнике АВС известны: длина стороны ВС и
величина угла С. Чтобы вычислить сторону АВ, нужно
знать:
А) АС;
В) ∠ В;
С) ∠ А;

10.

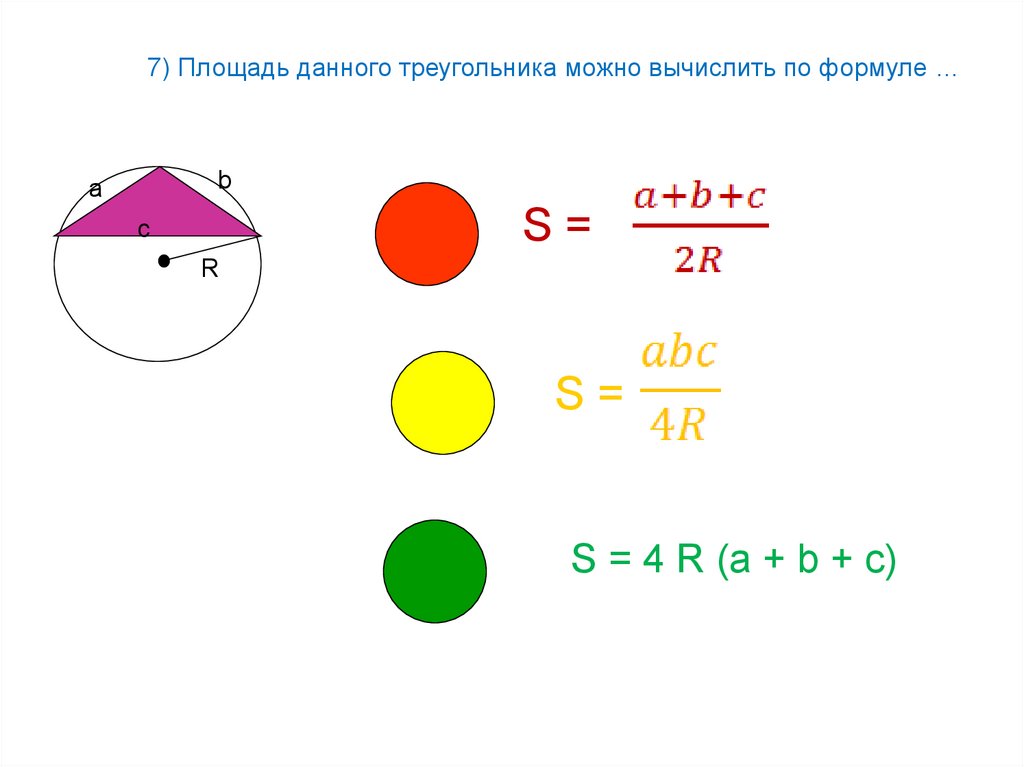
7) Площадь данного треугольника можно вычислить по формуле …
а
а
b
S=
с
R
S=
S = 4 R (a + b + c)

11. Станция «Реши треугольник»

• Команда «Считалкины» выполняет № 47 (стр.25) в
рабочей тетради.
• Команда «Решалкины» решает задачу № 1 с
использованием теоремы синусов.
• Команда «Смекалкины» решает задачу № 1 с
использование теоремы косинусов

12.

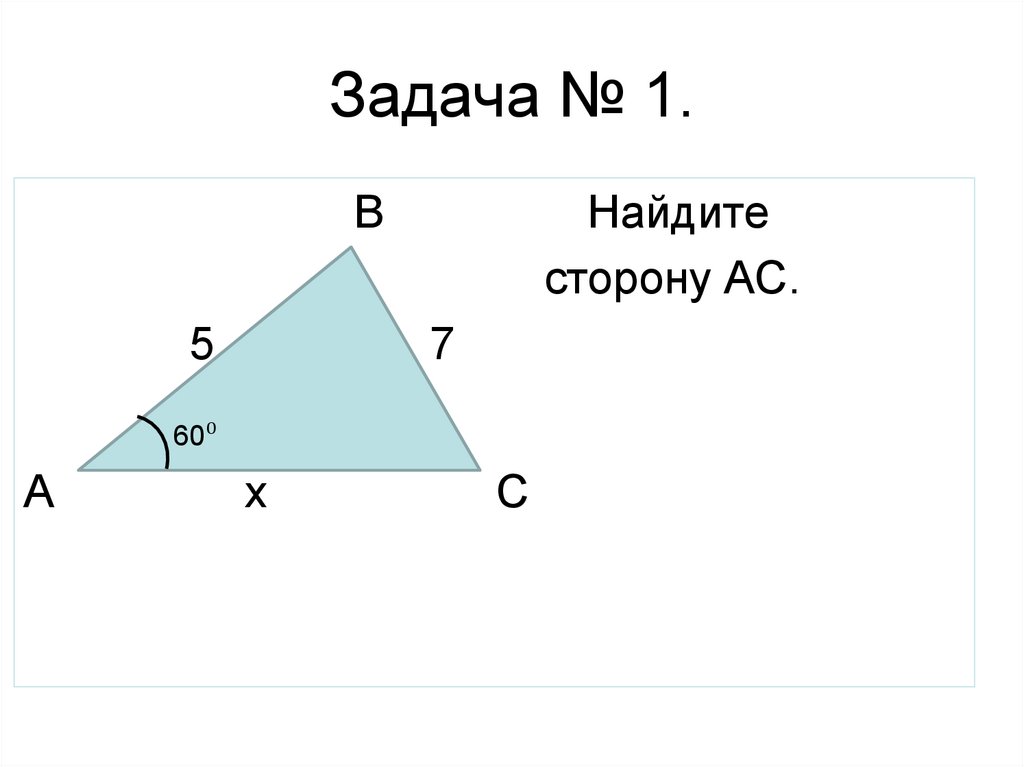
13. Задача № 1.

В
5
Найдите
сторону АС.
7
60⁰
А
х
С

14. Станция «Раз задачка, два задачка…»

Задача № 2
Одна из сторон треугольника равна 2,
а два его угла равны 45⁰ и 60⁰.
Найдите площадь треугольника.

15. Станция «Спортивная»

Физкультминутка
(выполнение упражнений для рук).
Руки подняли и покачали –
Это деревья в лесу.
Руки нагнили, кисти встряхнули –
Ветер сбивает росу.
В сторону руки, плавно помашем –
Это к нам птицы летят.
Как они сели, тоже покажем –
Руки мы сложим – вот так.

16. Станция «Практическая».

• Практические задачи для нахождения
расстояния до недоступных объектов
на местности.

17. ТЕОРЕМЫ Синусов и Косинусов . Нахождение расстояния до недоступного предмета .

Выполнила: Климанова Наташа
Ученица 9 «А» класса .

18.

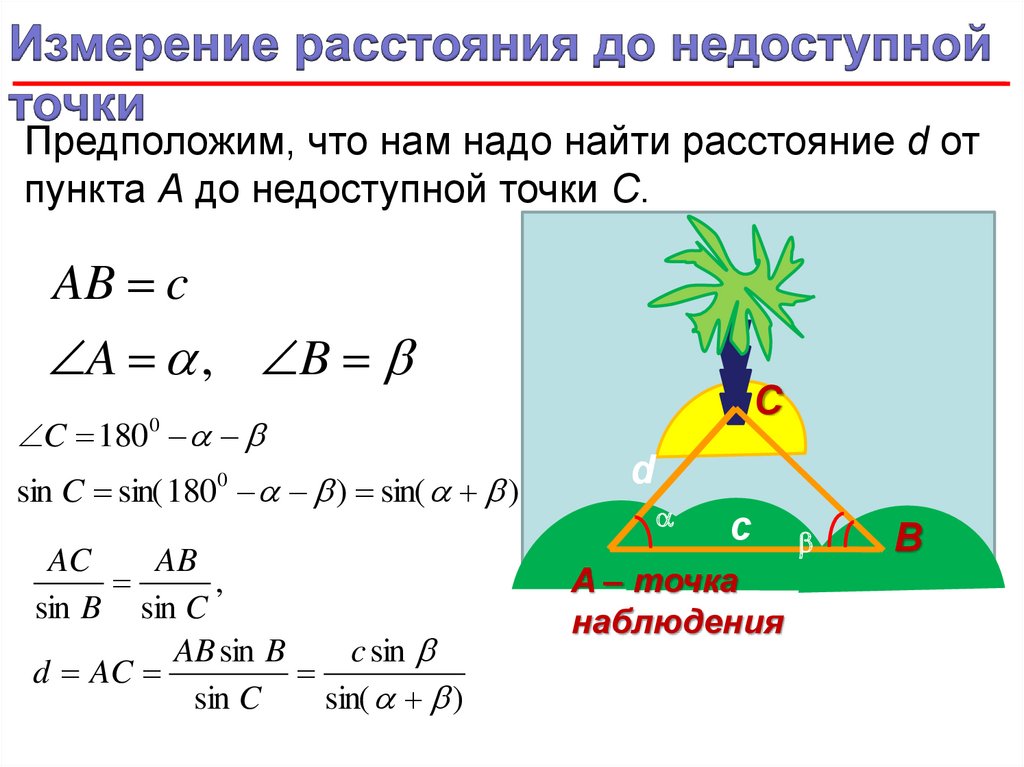
Предположим, что нам надо найти расстояние d от
пункта А до недоступной точки С.
AB c
A , B
С
C 180
0
sin C sin( 1800 ) sin( )
AC
AB
,
sin B sin C
AB sin B
c sin
d AC
sin C
sin( )
d
с
A – точка
наблюдения
B

19. Применение синусов и косинусов на практике.

Уткина Анна 9 «А»

20. Задача:

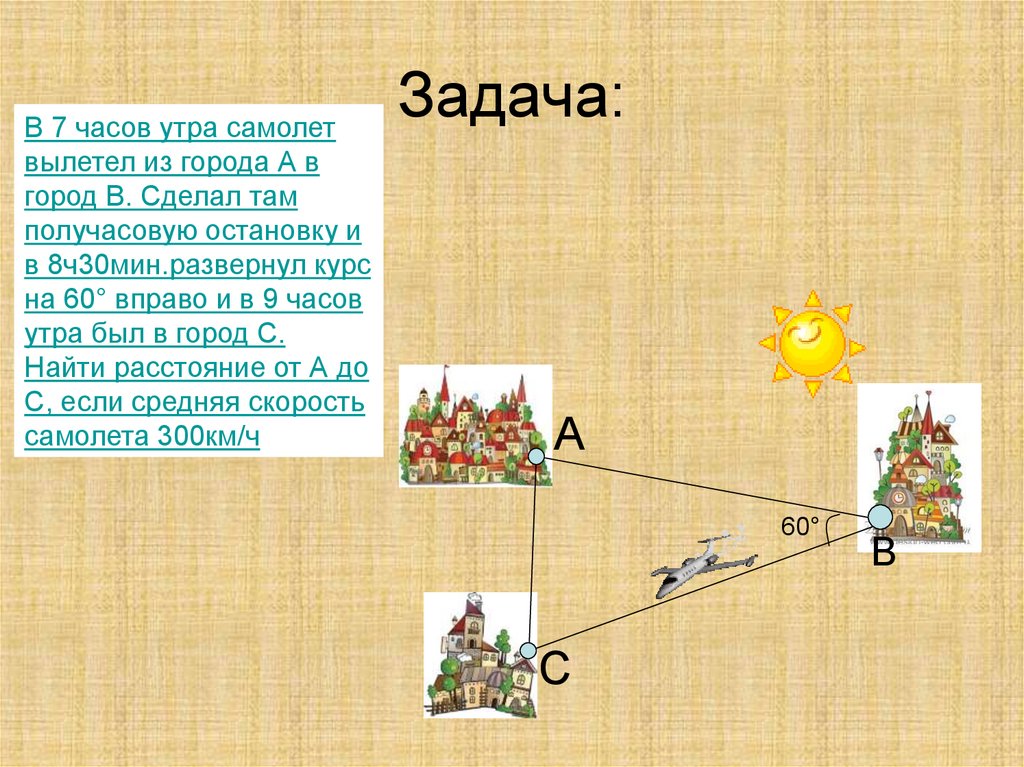
В 7 часов утра самолет
вылетел из города А в
город В. Сделал там
получасовую остановку и
в 8ч30мин.развернул курс
на 60° вправо и в 9 часов
утра был в город С.
Найти расстояние от А до
С, если средняя скорость
самолета 300км/ч
Задача:
А
60°
С
В

21.

Зименков Андрей, 9 а класс

22. Задача №1

С
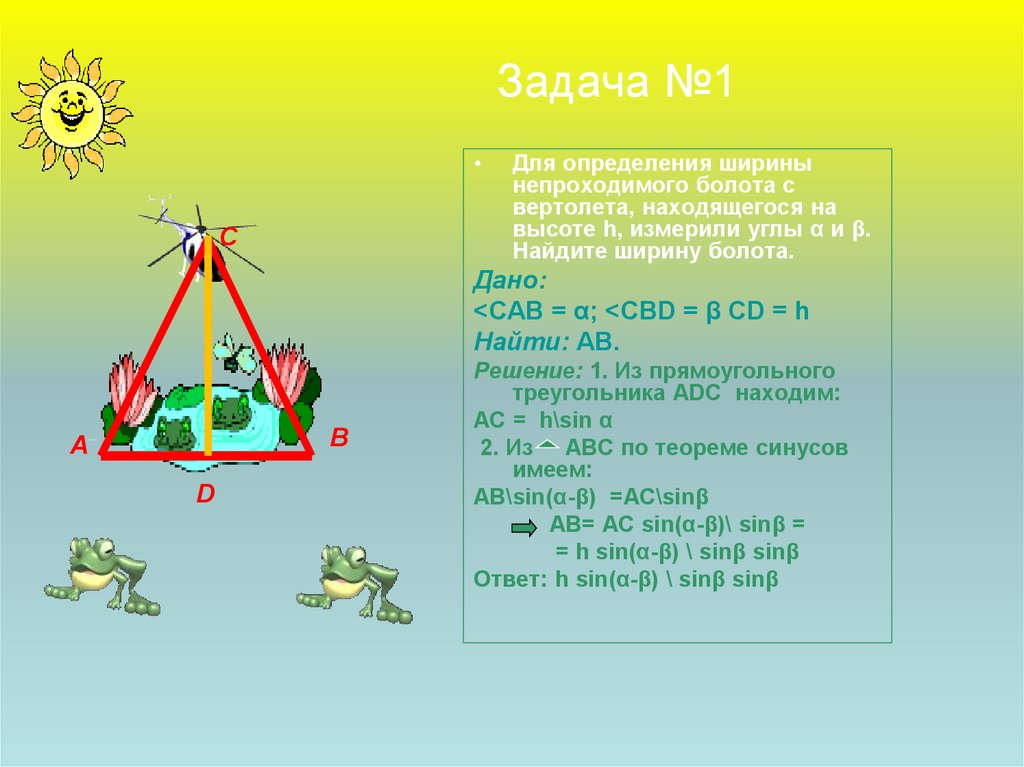
Для определения ширины
непроходимого болота с
вертолета, находящегося на
высоте h, измерили углы α и β.
Найдите ширину болота.
Дано:
<САВ = α; <СВD = β СD = h
Найти: АВ.
В
А
D
Решение: 1. Из прямоугольного
треугольника АDC находим:
АС = h\sin α
2. Из АВС по теореме синусов
имеем:
АВ\sin(α-β) =AC\sinβ
AB= AC sin(α-β)\ sinβ =
= h sin(α-β) \ sinβ sinβ
Ответ: h sin(α-β) \ sinβ sinβ

23.

Я люблю математику
не только потому, что
она находит
применение в жизни,
но и потому что она
красива.
Петер Роске