Similar presentations:
Решение треугольников. Теоремы синусов и косинусов
1.
Учитель: Маковская Ольга Михайловна2.
Цели урока:Познакомить учащихся с методами решения
треугольников;
закрепить знание учащимися теорем синусов
и косинусов;
научить применять эти теоремы в ходе
решения задач;
развивать логическое мышление, память,
математическую речь, прививать интерес к
геометрии;
воспитывать ответственное отношение к
учебному труду.
3.
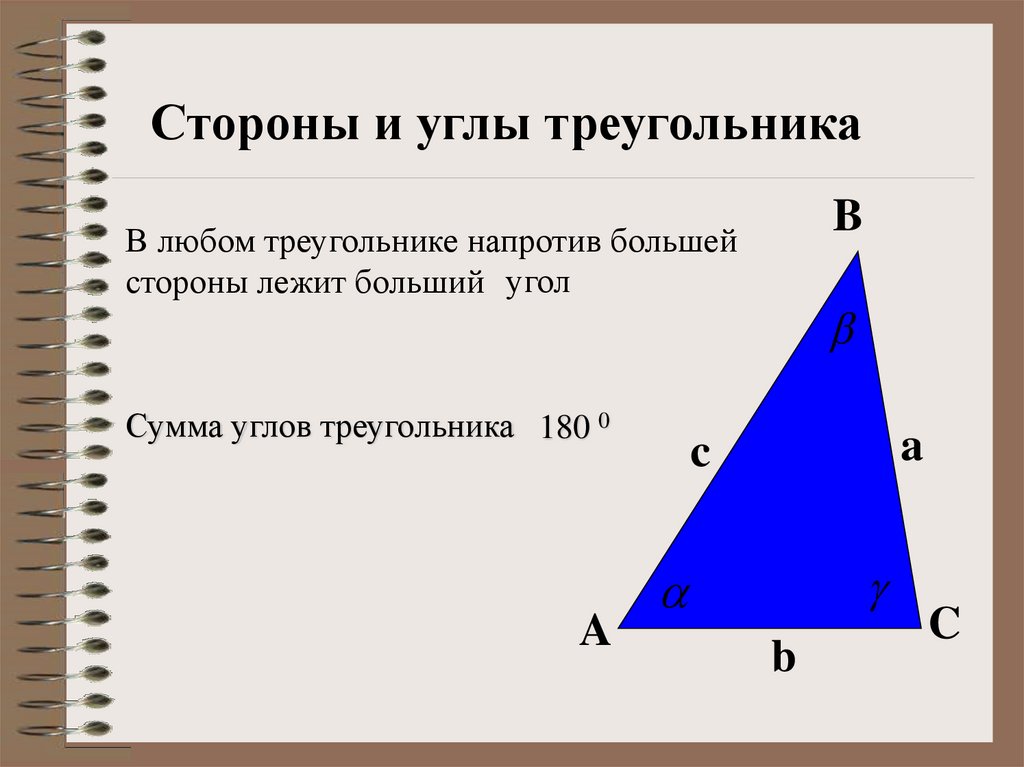
Стороны и углы треугольникаB
В любом треугольнике напротив большей
стороны лежит больший угол
Сумма углов треугольника 180 0
A
a
c
b
C
4. Синус, косинус и тангенс угла.
sin (90 – α) = cos αФормулы
приведения
cos (90 – α) = sin α
sin (180 – α)= sin α
cos (180 – α) = - cosα
5. Укажите значение синуса и косинуса углов
• α = 1500•β=
0
30
• γ = 1200
1
2
Sin α =
3
Cos α = - 2
1
Sin β = 2
3
Cos β = 2
3
Sin γ = 2
1
Cos γ = 2
6. Укажите градусную меру угла
22
1
2
• Sin β =
• Cos β =
3
• Sin γ = 2
• Cos γ = • Sin α = 1
0
45 ,
2
2
0
135
•β=
β=
0
• β = 60
• γ = 600, γ = 1200
• γ = 1350
0
• α = 90
7.
Теорема синусовB
a
b
c
sin sin sin
AB
BC
AC
sin C sin A sin B
a
c
A
b
C
8.
Запишите теорему синусовдля треугольника MNK
N
M
K
9.
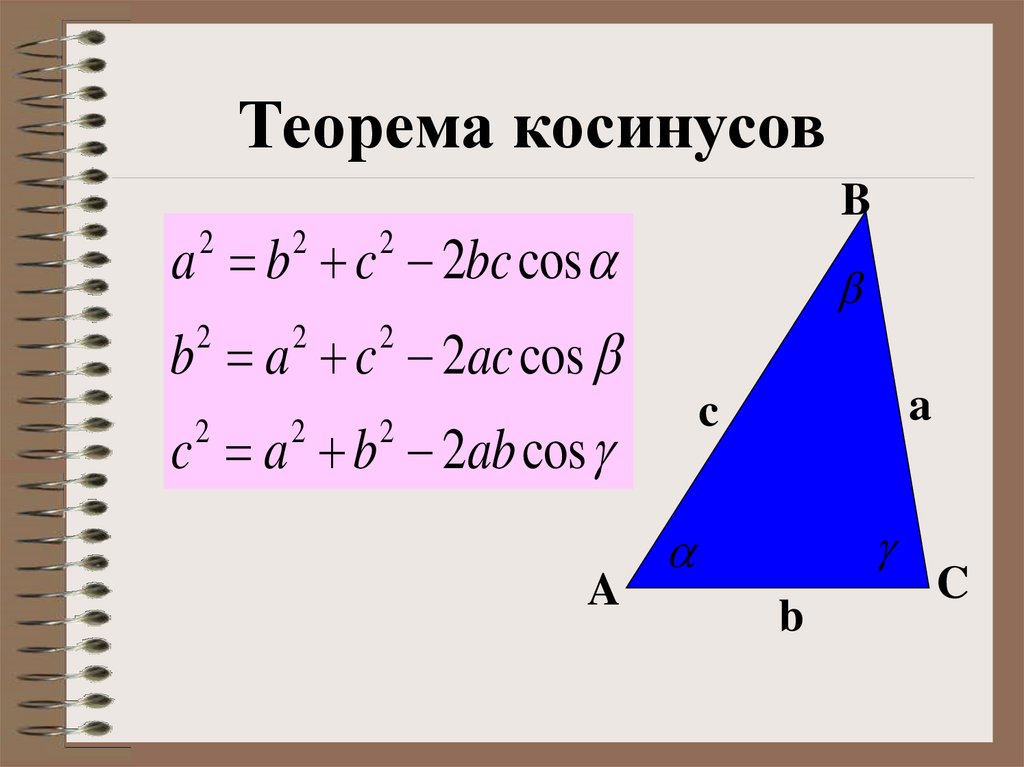
Теорема косинусовB
a b c 2bc cos
2
2
2
b a c 2ac cos
2
2
2
c a b 2ab cos
2
2
2
A
a
c
b
C
10.
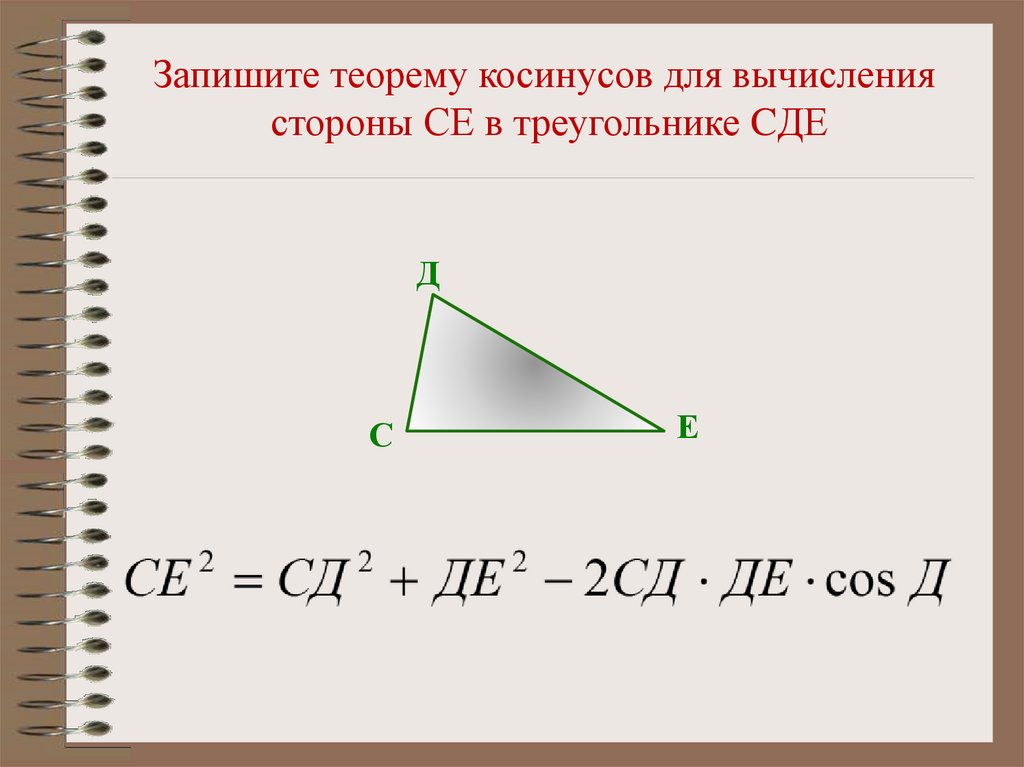
Запишите теорему косинусов для вычислениястороны СЕ в треугольнике CДЕ
Д
С
Е
11.
BЗадача
À
5
4
60
0
C
AB 5,AC 4
ACB 600
AB ?
Ответ: AB 21
12. Решение треугольников
Решить треугольник – этозначит найти его
неизвестные элементы по
известным.
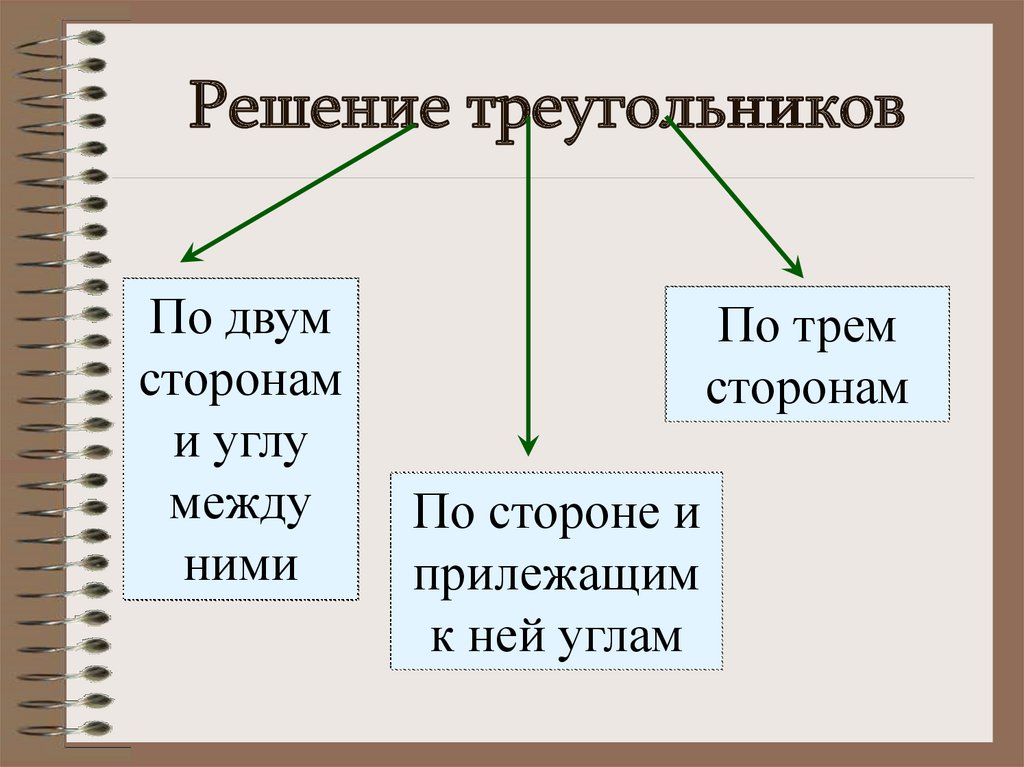
13. Решение треугольников
По двумсторонам
и углу
между
ними
По трем
сторонам
По стороне и
прилежащим
к ней углам
14. По двум сторонам и углу между ними
1. По теореме косинусов найти третью сторонуB
a b c 2bc cos
2
2
2
a b 2 c 2 2bc cos
2. По теореме косинусов найти один из
углов (β)
b 2 a 2 c 2 2ac cos
2ac cos a 2 c 2 b 2 A
a2 c2 b2
cos
2ac
c
По таблице Брадиса найти угол
3. γ=180 – α – β (сумма углов треугольника)
C
b
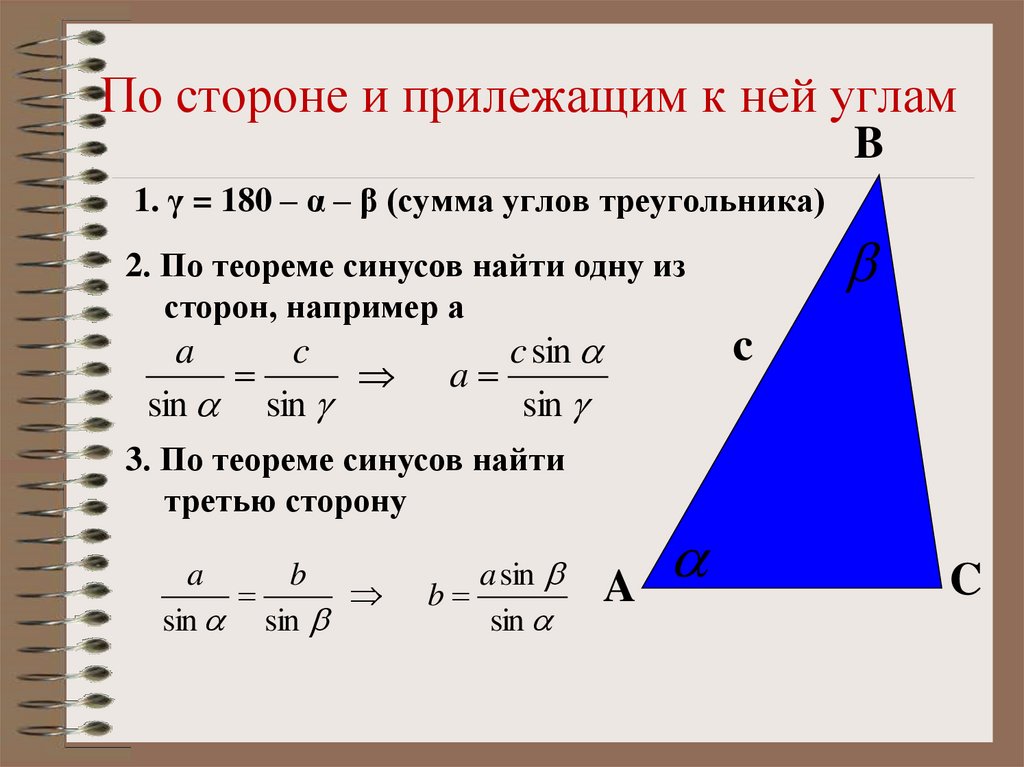
15. По стороне и прилежащим к ней углам
B1. γ = 180 – α – β (сумма углов треугольника)
2. По теореме синусов найти одну из
сторон, например а
a
c
sin sin
c sin
a
sin
c
3. По теореме синусов найти
третью сторону
a
b
sin sin
a sin
b
sin
A
C
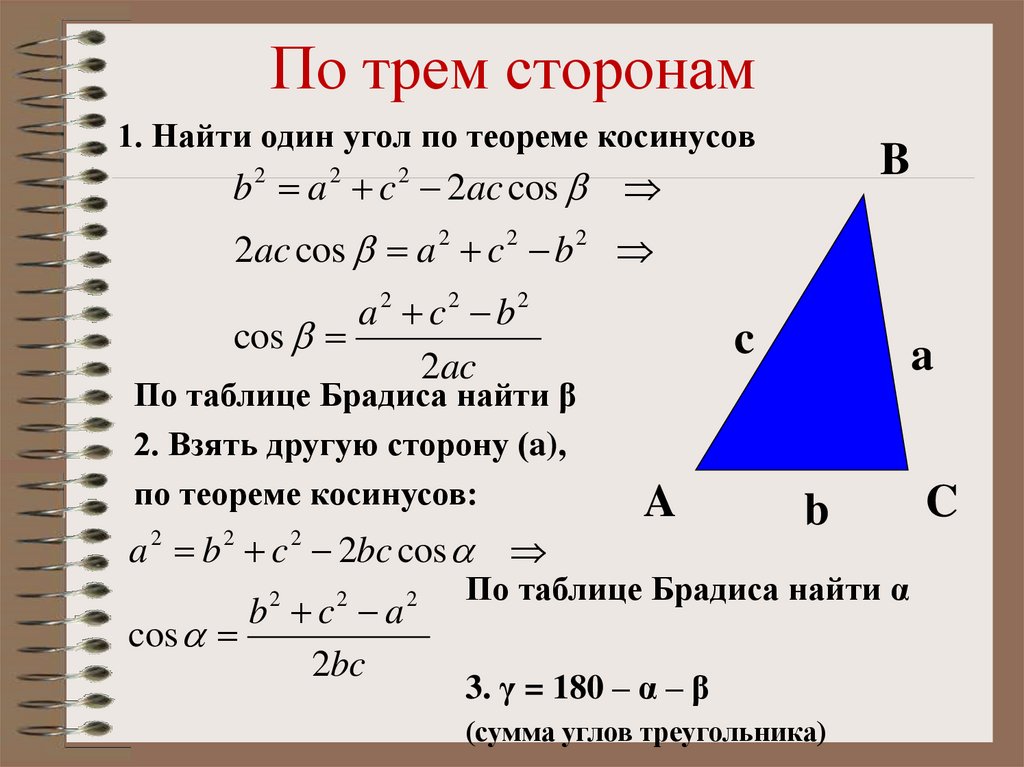
16. По трем сторонам
1. Найти один угол по теореме косинусовB
b a c 2ac cos
2
2
2
2ac cos a 2 c 2 b 2
a2 c2 b2
cos
2ac
По таблице Брадиса найти β
2. Взять другую сторону (a),
по теореме косинусов:
a 2 b 2 c 2 2bc cos
b c a
cos
2bc
2
2
2
c
A
a
b
По таблице Брадиса найти α
3. γ = 180 – α – β
(сумма углов треугольника)
C
17. Пример.
Дано: a = 5; β =γ = 450
Найти: b, с, α.
A
300
Решение:
1050
2,59
C
3,66
300
45 0
5
1. α = 1800 – β – γ = 1800 - 300 - 450 = 1050
a sin 5 sin 300
b
sin
sin 1050
5 0,5
0
0
0
sin 30 0,5 ; sin 105 sin 75 0,9659 ; b
2,59
0,9659
a
c
a sin 5 sin 450 5 0,7071
c
3,66
3.
0
sin sin
sin sin 105
0,9659
a
b
2.
sin sin
B
18.
Решение задач - пример № 1.Дано:
Решение:
a = 20 см γ = 180° - (β + )
= 75 °
β = 60°
γ = 180° - (75° + 60°) = 45°
a / sin = b / sin β = c / sin γ
β
с
a
γ
b
Найти:
b = a (sin β / sin γ)
γ-?
b = 20 (sin 60° / sin 75°) 20 (0,866 / 0,966) 17,9
b-?
c = a (sin γ / sin )
c-?
c = 20 (sin 45° / sin 75°) 20 (0,7 / 0,966) 14,6
Ответ: 45°; 17,9 см; 14,6 см.
Далее
19.
Дано:a=7м
Решение задач - пример № 2.
Решение:
a
c = a ² + b ² - 2 a b cos γ
b = 23 м
γ = 130°
Найти:
- ?
β - ?
c-?
c
β
γ
c = 49 + 529 – 2 7 23 (- 0,643) 28
b
cos = (b ² + c ² - a ²) / 2 b c
cos = (529 + 784 – 49) / 2 23 28 0,981
11°
β =180° - ( + γ) = 180° - (11° + 130°) 39°
Ответ: 28 см; 39°; 11°.
Далее
20.
Решение задач - пример № 3.Дано:
a = 7 см
b = 2 см
c = 8 см
Найти:
- ?
β - ?
γ - ?
Решение:
cos = (b ² + c ² - a ²) / 2 b c
β
c
cos = (4 + 64 – 49) / 2 2 8 0,981
a
54°
cos β = (a ² + c ² - b ²) / 2 a c
cos β = (49 + 64 – 4) / 2 7 8 0,973
β 13°
γ
b
γ 180° - ( + β) = 180° - (54° + 13°) = 113°
Ответ: 54°; 13°; 113°.
Далее
21.
Рефлексия.•Я сегодня таскал
тяжёлые камни.
•Я сегодня добросовестно
выполнял свою работу.
•Я сегодня строил храм.
















 mathematics
mathematics








