Сумма углов треугольника

1.

A
C
B

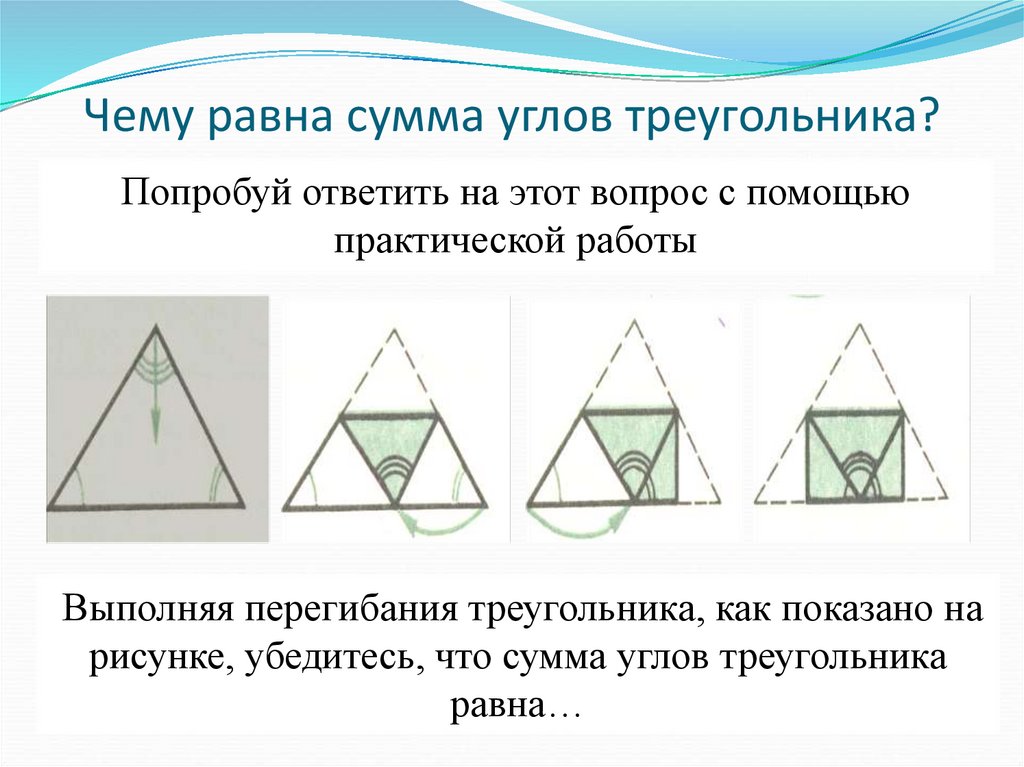
2. Чему равна сумма углов треугольника?

Попробуй ответить на этот вопрос с помощью
практической работы
Выполняя перегибания треугольника, как показано на
рисунке, убедитесь, что сумма углов треугольника
равна…

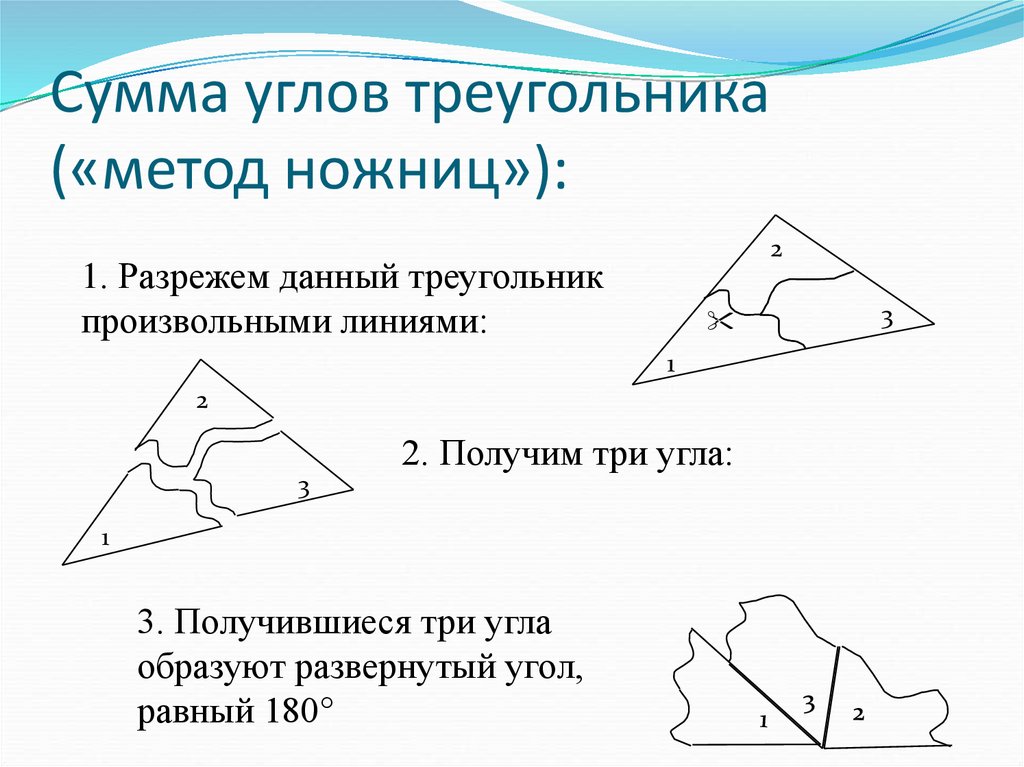
3. Сумма углов треугольника («метод ножниц»):

2
1. Разрежем данный треугольник
произвольными линиями:
1
2
2. Получим три угла:
3
1
3. Получившиеся три угла
образуют развернутый угол,
равный 180°
3

4.

Историческая справка
a
5
2
4
Дано: a || b
Доказательство
данного
факта,
4 60
изложенное в современных учебниках,
5 80
Найти: 1; 2; 3.
содержалось
ещё
в
комментарии
к
b
1
3
«Началам»
Евклида
древнегреческого
учёного Прокла (V в.н.э.) Прокл утверждает,
что доказательство теоремы было открыто
ещё пифагорейцами (Vв.до н.э.).

5.

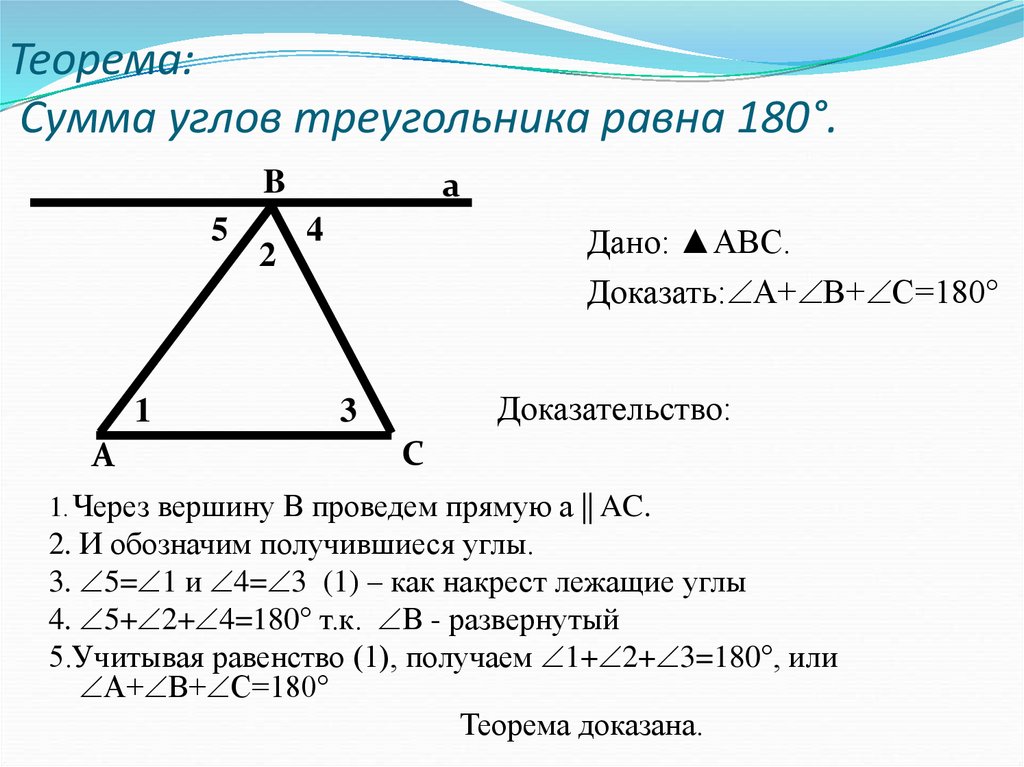
Теорема:
Сумма углов треугольника равна 180°.
B
5
1
A
2
а
4
Дано: ▲АВС.
Доказать: А+ В+ С=180°
Доказательство:
3
C
1. Через вершину В проведем прямую а || AC.
2. И обозначим получившиеся углы.
3. 5= 1 и 4= 3 (1) – как накрест лежащие углы
4. 5+ 2+ 4=180° т.к. В - развернутый
5.Учитывая равенство (1), получаем 1+ 2+ 3=180°, или
А+ В+ С=180°
Теорема доказана.

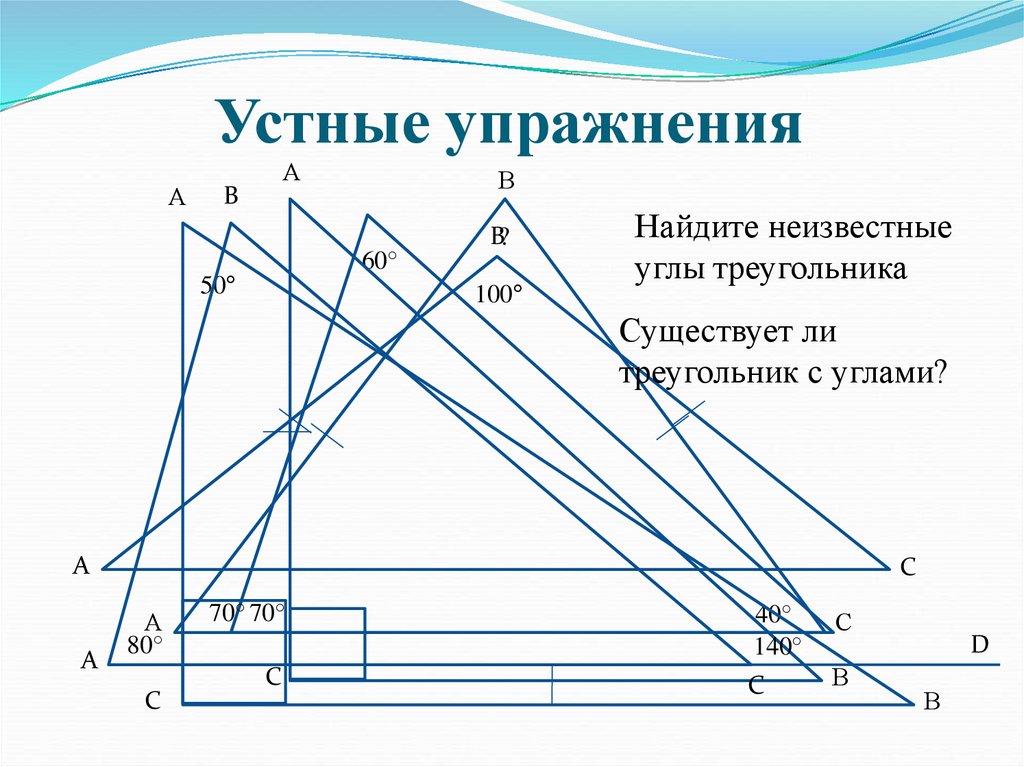
6. Устные упражнения

А
А
B
В
В?
60°
50°
100°
Найдите неизвестные
углы треугольника
Существует ли
треугольник с углами?
А
А
С
А
80°
С
70° 70°
С
40°
140°
С
C
В
D
В

7. Решите задачу

B
2
Доказать: ∠4=∠1+∠2
1
1
А
3
4
D
C
Внешним углом треугольника называется угол,
смежный с каким – нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов
треугольника, не смежных с ним.

8.

Может ли быть в треугольнике
два прямых угла?
Может ли быть в треугольнике
два тупых угла?
Может ли быть в треугольнике
прямой и тупой углы?

9.

B
D
Дано: AB = BC = 5 см,
Дано: DK – биссектриса,
∠BCD = 120°.
∠EDK = 28°,
Найти:=P
∆ABC.
∠CKD
75°.
Найти: углы ∆CDE.
28°
C
A
75°
K
120°
C
E
D

10.

Закончите приведенные ниже предложения, чтобы
получились верные утверждения:
1. Сумма углов произвольного треугольника равна…?
2. Если один из углов треугольника тупой, то
остальные…?
3. Один из внешних углов треугольника равен 100°.
Сумма двух углов треугольника, не смежных с ним
равна…?
4. Если все внешние углы треугольника тупые, то
углы треугольника…?
5. Если один из углов равнобедренного треугольника
равен 60°, то треугольник…?

11.

Дома: п. 30,
№223(в), 227(а).