Similar presentations:
Треугольник. Виды треугольников
1. Урок геометрии 8 классе
2.
Бермудские острова,владение
Великобритании в
северо-западной части
Атлантического
океана, близ берегов
Северной Америки.
Острова были
открыты испанским
мореплавателем Х.
Бермудесом в 1522 г.
3.
Пуэрто-Рико,содружество ПуэртоРико, владение США в
Вест-Индии, на острове
Пуэрто-Рико и близ
лежащих островах
Флорида, полуостров
на юго-востоке
Северной Америки,
часть штата Флорида
(США).
4.
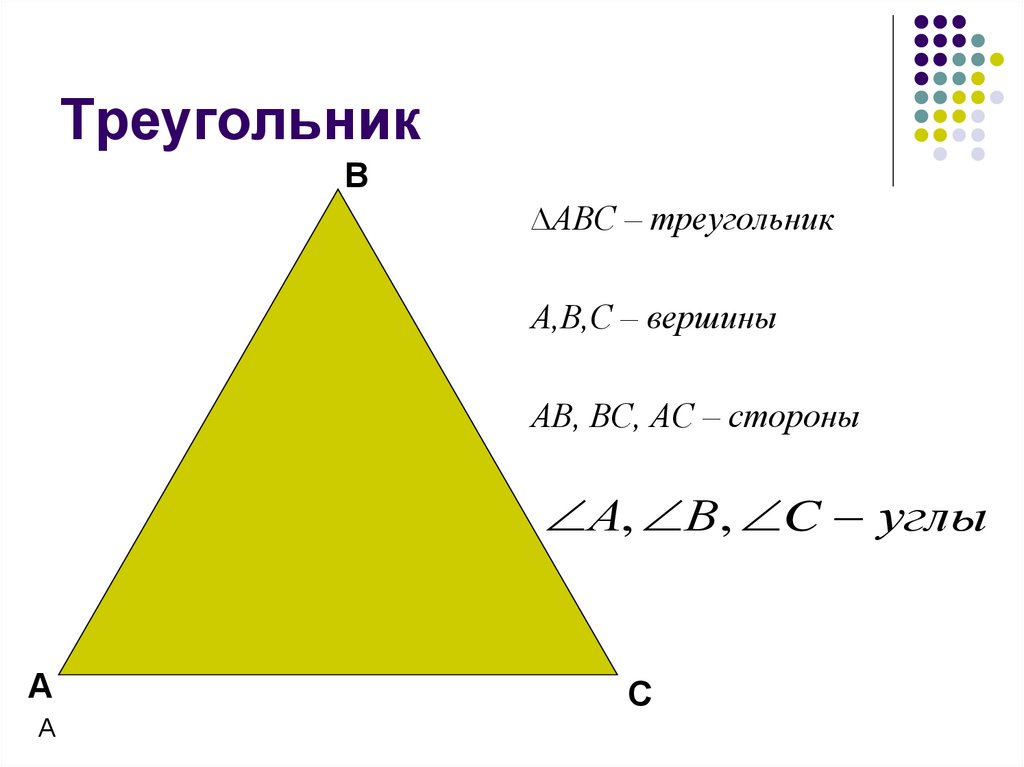
5. Треугольник
В∆АВС – треугольник
А,В,С – вершины
АВ, ВС, АС – стороны
А, В, C углы
А
А
С
6.
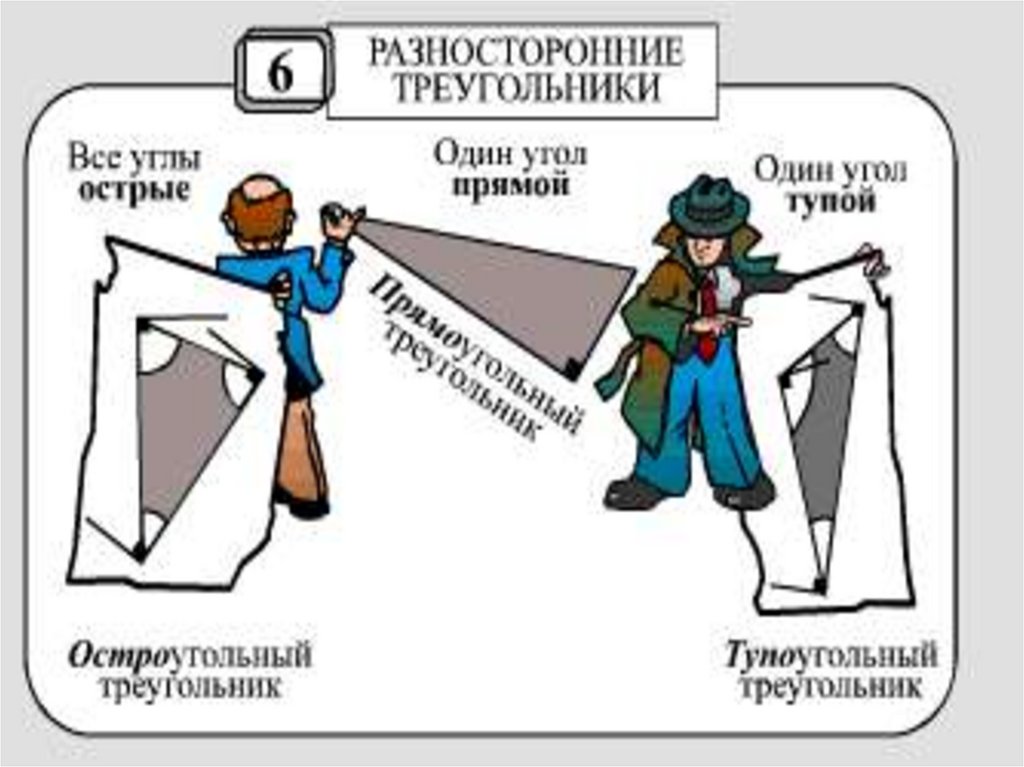
7.
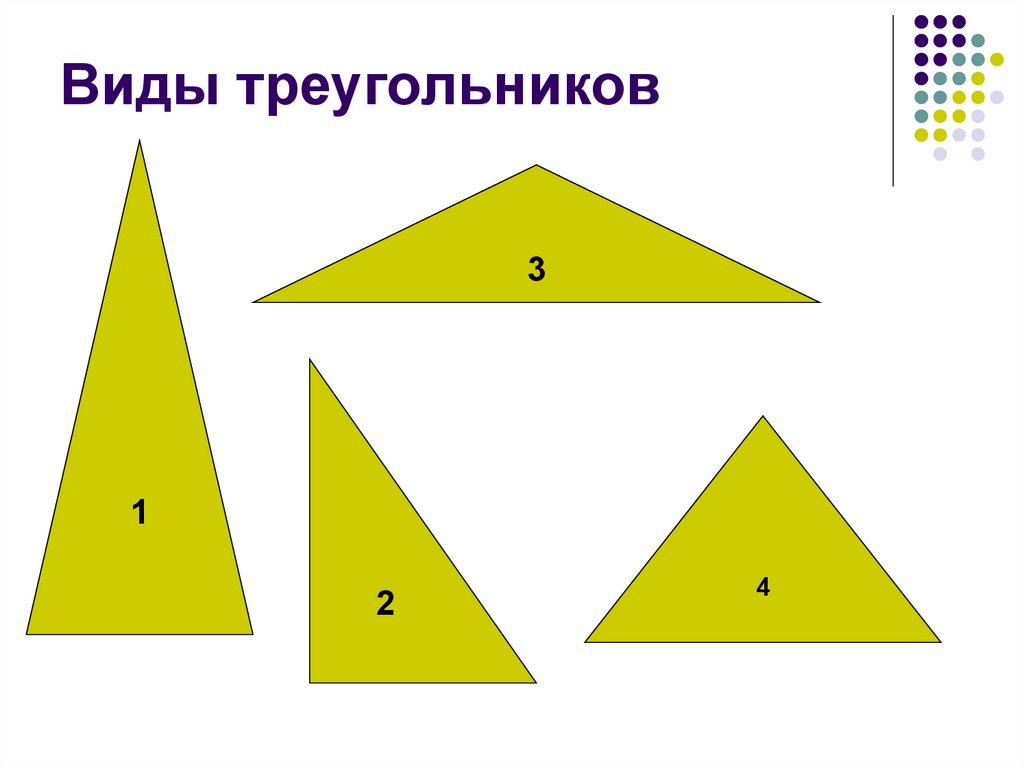
Виды треугольников3
1
2
4
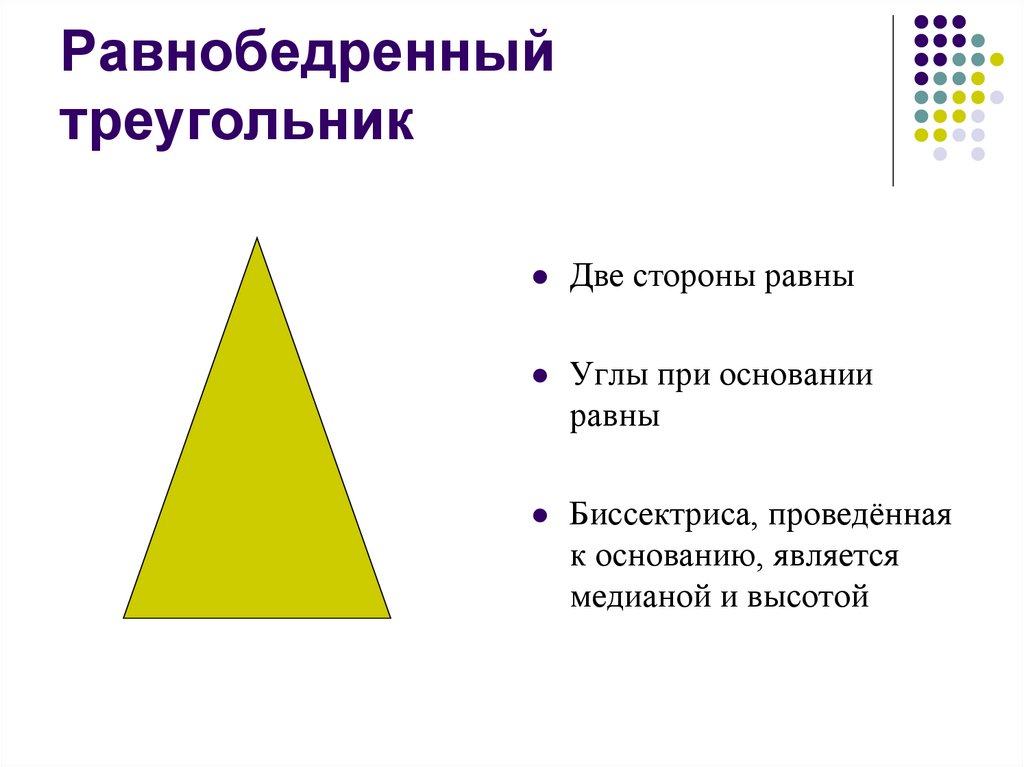
8. Равнобедренный треугольник
Две стороны равныУглы при основании
равны
Биссектриса, проведённая
к основанию, является
медианой и высотой
9. Равносторонний треугольник
Все стороны равныУглы все равны
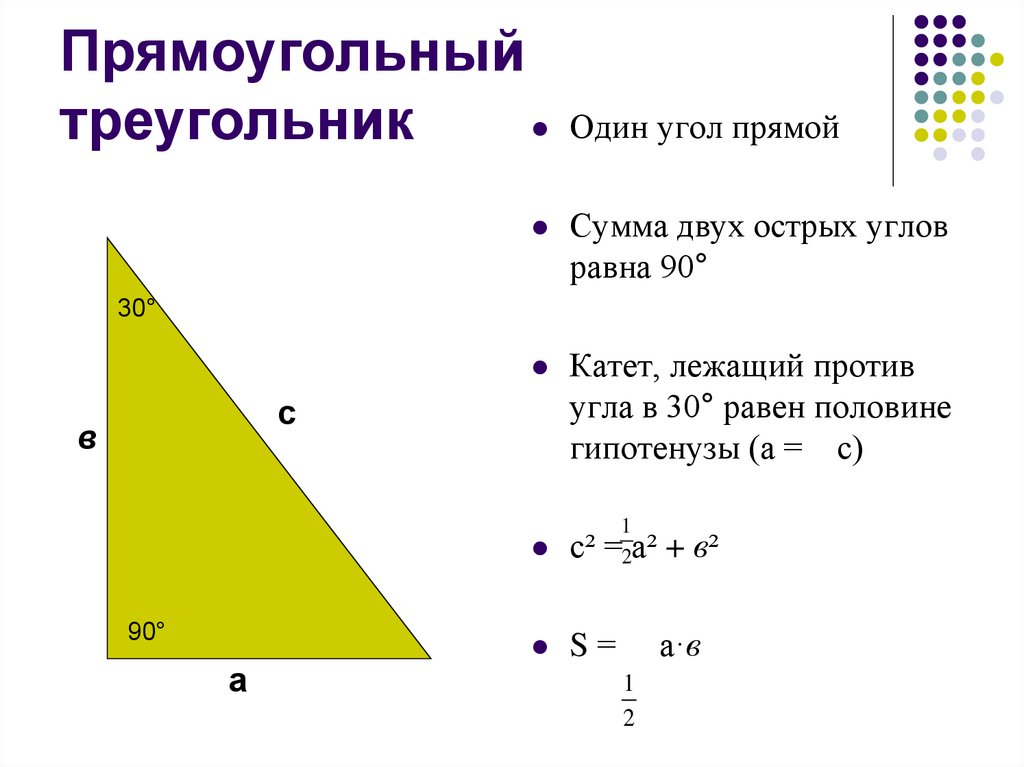
10. Прямоугольный треугольник
Один угол прямойСумма двух острых углов
равна 90°
Катет, лежащий против
угла в 30° равен половине
гипотенузы (а = с)
30°
с
в
90°
а
1
=2а²
с²
S=
+ в²
а·в
1
2
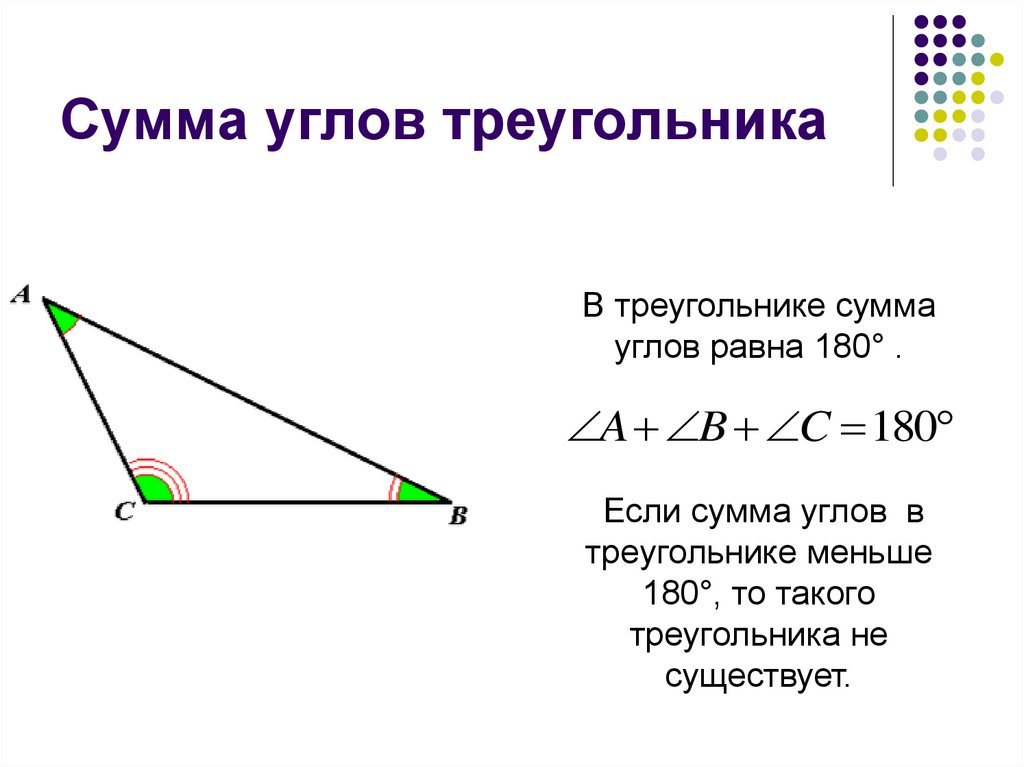
11. Сумма углов треугольника
В треугольнике суммауглов равна 180° .
A B C 180
Если сумма углов в
треугольнике меньше
180°, то такого
треугольника не
существует.
12. Признаки равенства
По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней углам
По трём сторонам
13. ФАЛЕС
Древнегреческий учёный ифилософ, основатель
ионийской(милетской)
школы. Фалес первым стал
доказывать геометрические
теоремы.
14. Пирамида Хеопса
Фараон IV династии Хеопсвоздвиг самую большую из
египетских пирамид, которая
была самым высоким
сооружением в течении
последующих 4 тысячелетий
(высота пирамиды – 146,6 м,
длина каждой из сторон
основания – 230 м). На
постройку пирамиды Хеопса
ушло около 2,3 миллиона
каменных блоков весом до
2,5 т.
15. «Подобные треугольники»
16. Работа с текстом учебника
“+” – это я знаю и согласен;“ –” – в этом я сомневаюсь, не согласен;
“!” – это интересно и ново, неожиданно;
“?” – это непонятно, надо получить дополнительную
информацию и объяснения учителя.
17. Подобные фигуры
18.
19.
20. Как можно назвать эти фигуры?
21. Что из прочитанного оказалось неизвестным?
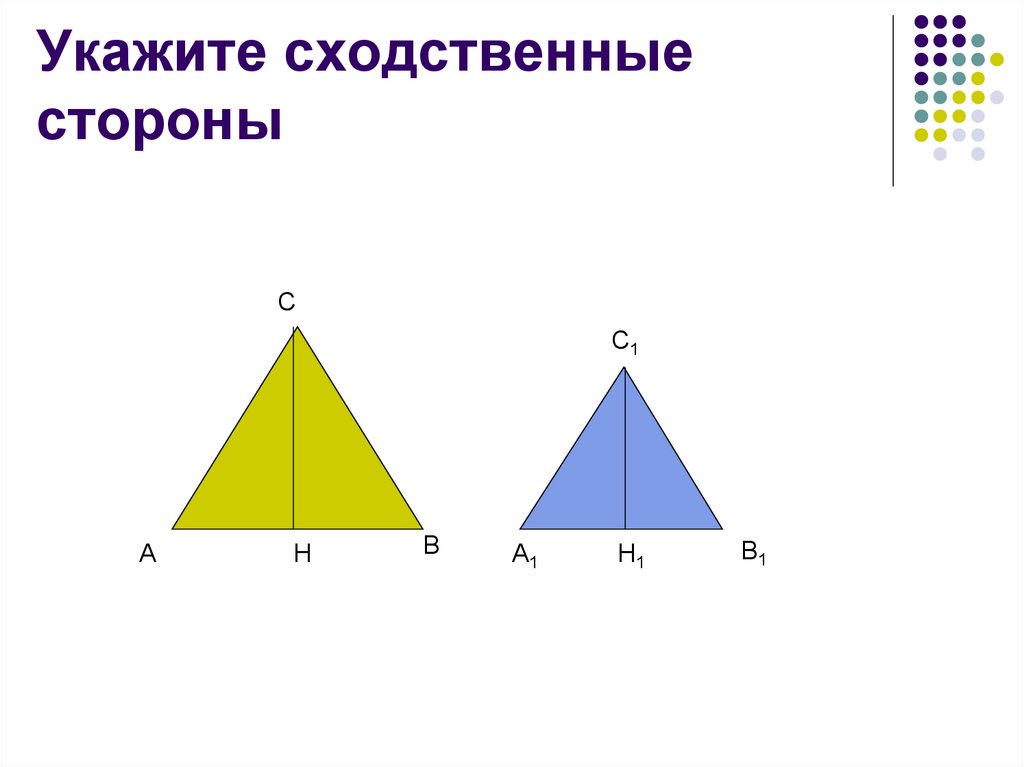
22. Укажите сходственные стороны
CC1
A
H
B
A1
H1
B1
23. Подобные треугольники – это
Похожие, одинаковые, пропорциональныеСходственные стороны:
АВ и A1B1, ВС и B1C1, АС и A1C1
C1
Равные углы: ∠A=∠A1,∠B=∠B1,∠C=∠C1
Сходственные стороны пропорциональны:
C
АВ
ВС
АС
к - коэффициент подобия
А1 В1 В1С1 А1С1
A1
A
Δ АВС ~ Δ A1 B1 C1
B1
B
24. Задача №1
Дано: ∆АВС и ∆МNK<А = 63°,<В = 56°
АВ = 4,ВС = 3, АС = 6
<M = 63°, <N =56°
МN = 8, NК = 6, МК = 12
Определите подобны ли
треугольники?
Задача № 2
Дано: ∆АВС подобен ∆MNK
<А = 30°, <В = 85°, <С = 65°.
Создать по данным задачи
модели подобных треугольников.
25. Укажите подобные фигуры
26. Домашнее задание: 1. Всем: придумать способ измерения высоты пирамиды. 2. Для 1 группы: подготовить рисунки или макеты подобных
фигур.3. Для 2 группы: подготовить историческую справку о
Фалесе Милетском.
27. СИНКВЕЙН
1 строка – одно слово – названиестихотворения, существительное.
2 строка – два слова (прилагательные).
3 строка – три слова (глаголы).
4 строка – четыре слова – предложение.
5 строка – одно слово – ассоциация,
существительное.




















 mathematics
mathematics








