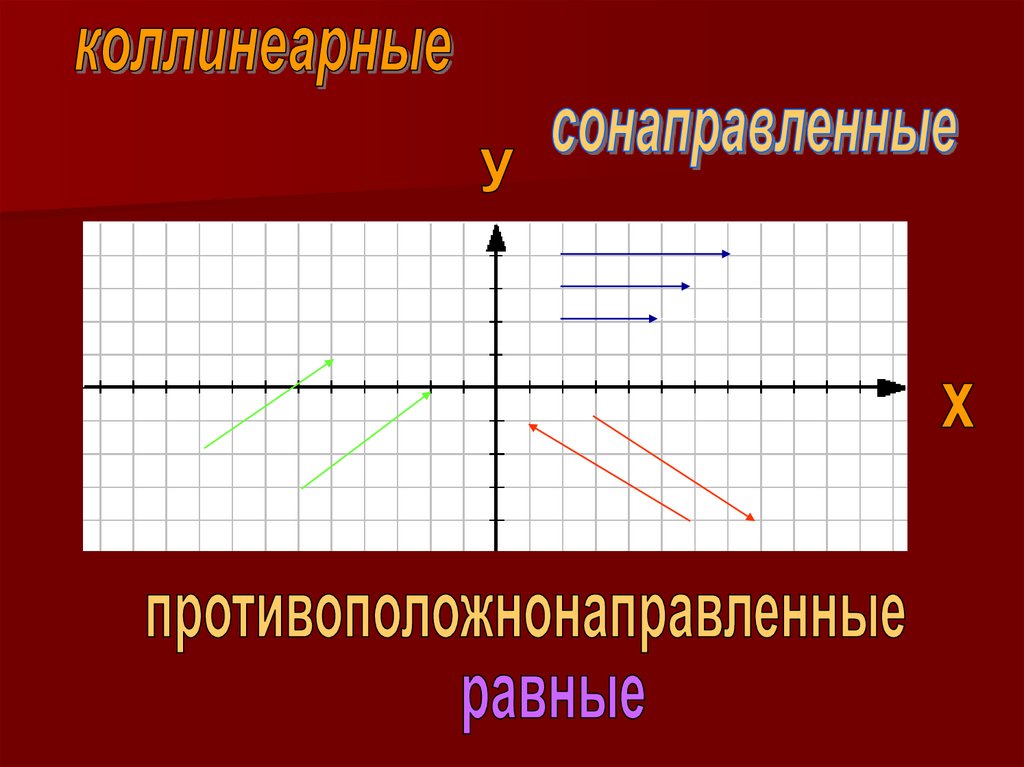
Метод координат

1. Решение задач по теме : МЕТОД КООРДИНАТ

2.

а {4;3}

3.

4.

№976 Найдите координаты точки пересечения
прямых
4х+3у-6=0 и 2х+у-4=0.
Ур. Прямой :
ах+ву+с=0
4х+3у-6=0
2х+у-4=0
Способ подстановки
У=
4х+3(
)-6=0
-2х=-6
Х=
У=4-2х=4-2*
(3;-2)
=

5.

№978 Начертите прямую, заданную
уравнением: а)у=3; б) х=-2; в) у=-4; г) х=7
ах+ву+с=0
у=3
Частные случаи:
||ох у=у0
х=7
||оу х=х0
у=-4
х=-2

6.

АВ{ х2-х1;у2-у1}
т.С (х2+х1;у2+у1)
2
2
|АВ|=√х2+у2
d=√ (х2-х1
)2 +( у
2-у1
(х-х0)2 + (у-у0)2 =r2
Х2 + у2 = r2
ах+ву+с=0
)2
1 вариант
2 вариант
{2;4}
{ 5; 0}
(1; 4,5)
(3; 0,5)
5
5
√10
3√2
(х+2)2 + у2 =9
(х+2)2 + (у-1)2
=25
Х2 + у2 =2
Х2 + у2 =3
Колич.бал.:
Оценка:
Колич.бал.:
Оценка:
12-13 б.- оценка «5»
10-11б.- оценка «4»
6-9 б.- оценка «3»
0-5- б.- оценка «2»

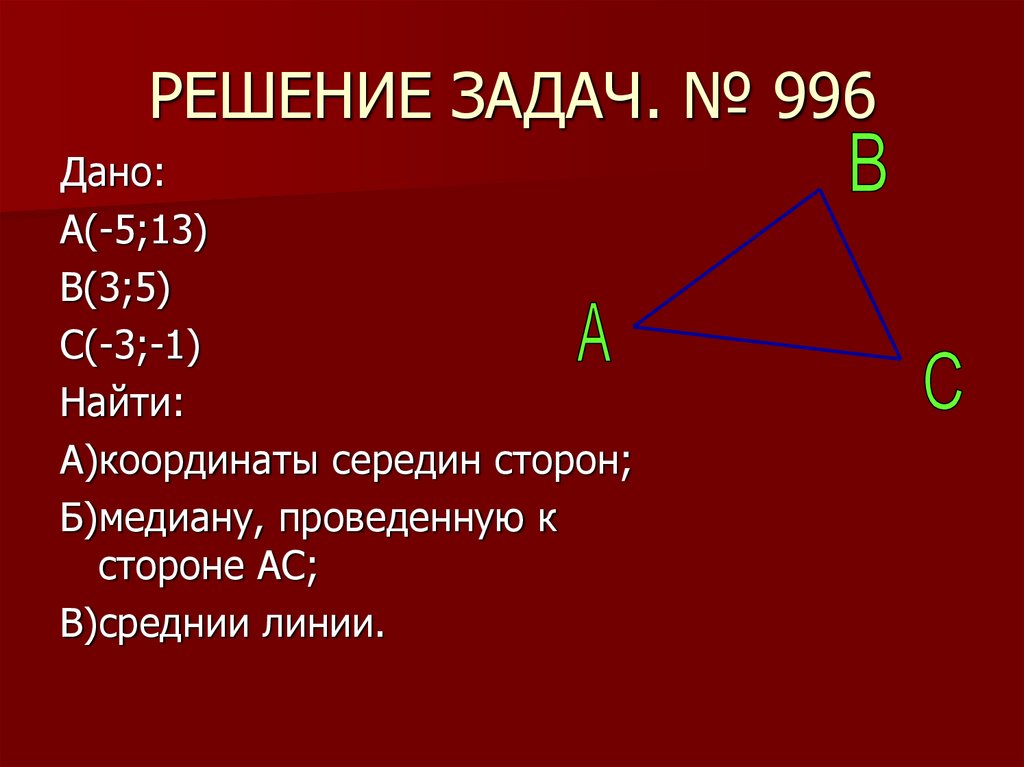
7. РЕШЕНИЕ ЗАДАЧ. № 996

Дано:
А(-5;13)
В(3;5)
С(-3;-1)
Найти:
А)координаты середин сторон;
Б)медиану, проведенную к
стороне АС;
В)среднии линии.

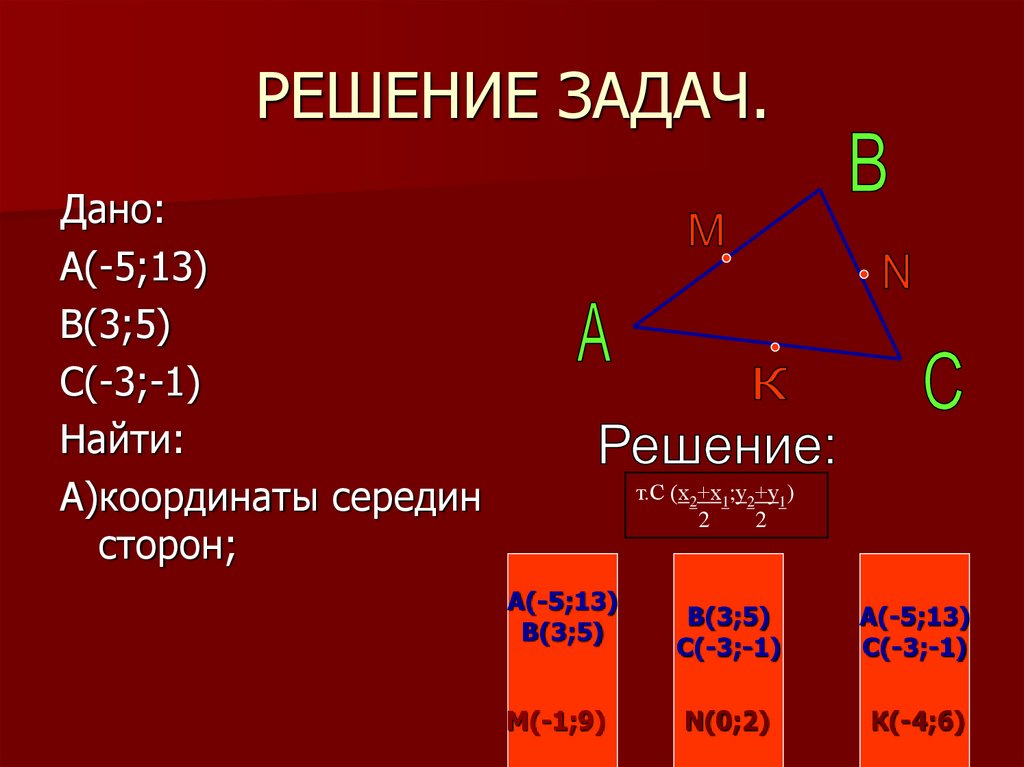
8. РЕШЕНИЕ ЗАДАЧ.

Дано:
А(-5;13)
В(3;5)
С(-3;-1)
Найти:
А)координаты середин
сторон;
т.С (х2+х1;у2+у1)
2
2
А(-5;13)
В(3;5)
М(-1;9)
В(3;5)
С(-3;-1)
А(-5;13)
С(-3;-1)
N(0;2)
К(-4;6)

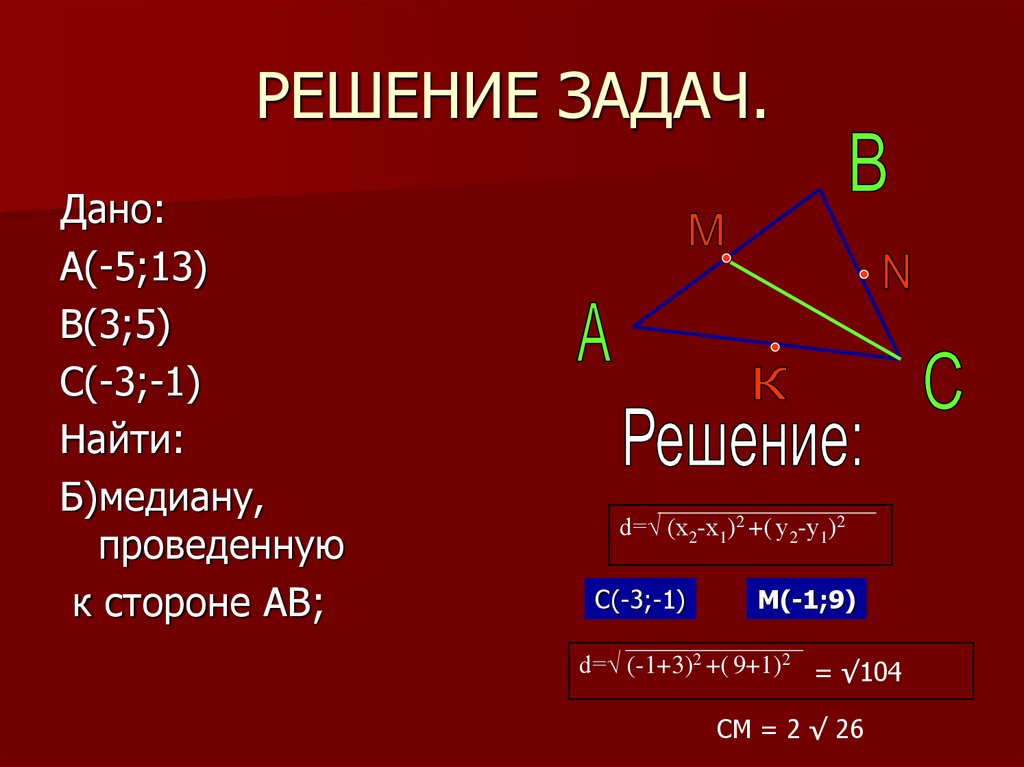
9. РЕШЕНИЕ ЗАДАЧ.

Дано:
А(-5;13)
В(3;5)
С(-3;-1)
Найти:
Б)медиану,
проведенную
к стороне АВ;
d=√ (х2-х1)2 +( у2-у1)2
С(-3;-1)
М(-1;9)
d=√ (-1+3)2 +( 9+1)2 = √104
СМ = 2 √ 26

10. РЕШЕНИЕ ЗАДАЧ.

Дано:
А(-5;13)
В(3;5)
С(-3;-1)
Найти:
В)среднии линии.
d=√ (х2-х1)2 +( у2-у1)2
М(-1;9)
√50 =
N(0;2)
5 √2

11. № 992

Дано:
А(4;8)
В(12;11)
С(7;0)
Док-ть, что
р/б треугольник
(2 стороны равны)
d=√ (х2-х1)2 +( у2-у1)2
АВ= √73
ВС= √146
СА= √73
АВ = СА ≠ ВС,
Значит треугольник
Равнобедренный, но
не равносторонний

12. №997

Дано:
А(3;2)
В(0;5)
С(-3;2)
Д(0;-1)
Док-ть, что
АВСД- квадрат.
1)Стороны равны
2)Диагонали равны
d=√ (х2-х1)2 +( у2-у1)2
СТОРОНЫ:
АВ= 3√2
ВС= 3√2
СД= 3√2
ДА= 3√2
1)Стороны равны
ДИАГОНАЛИ:
АС= 6
ВД= 6
2)Диагонали равны
ВЫВОД:
АВСД- квадрат.

13. Помогает ли метод координат решать геометрические задачи?