Similar presentations:
Метод координат
1. МЕТОД КООРДИНАТ
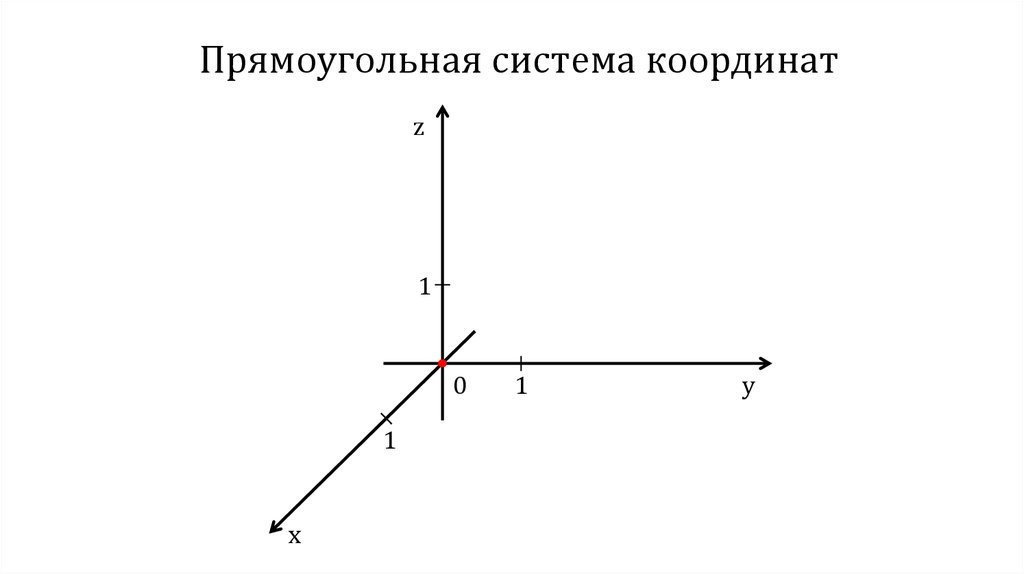
2. Прямоугольная система координат в пространстве
3.
Прямоугольная система координатz
1
0
1
x
1
y
4.
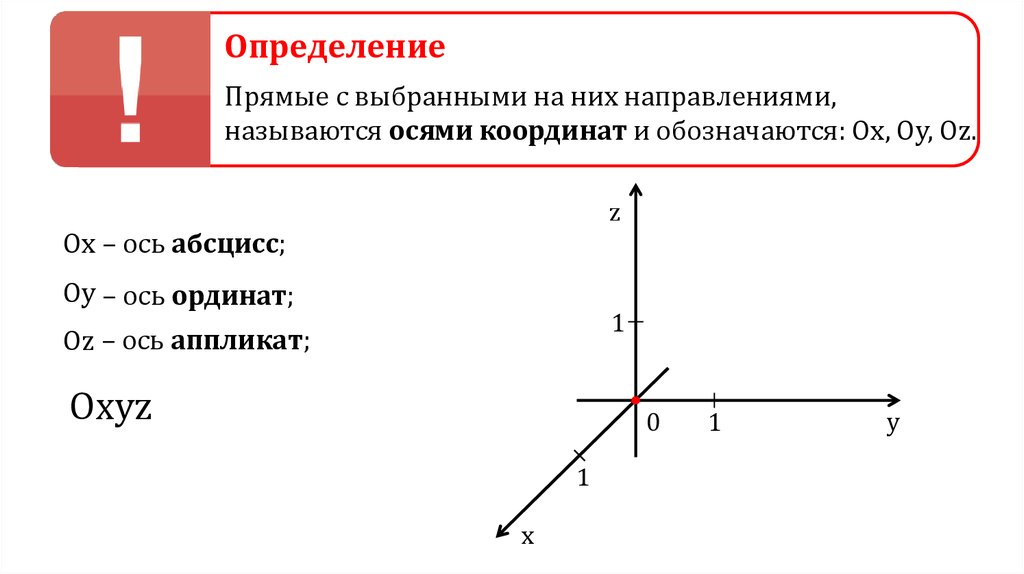
ОпределениеПрямые с выбранными на них направлениями,
называются осями координат и обозначаются: Ох, Оy, Оz.
z
Ох – ось абсцисс;
Оy – ось ординат;
1
Оz – ось аппликат;
Oxyz
0
1
x
1
y
5.
zz
1
1
0
1
x
1
0
y
z
Оху
x
1
0
x
1
1
Оzх
y
1
1
Оуz
y
6.
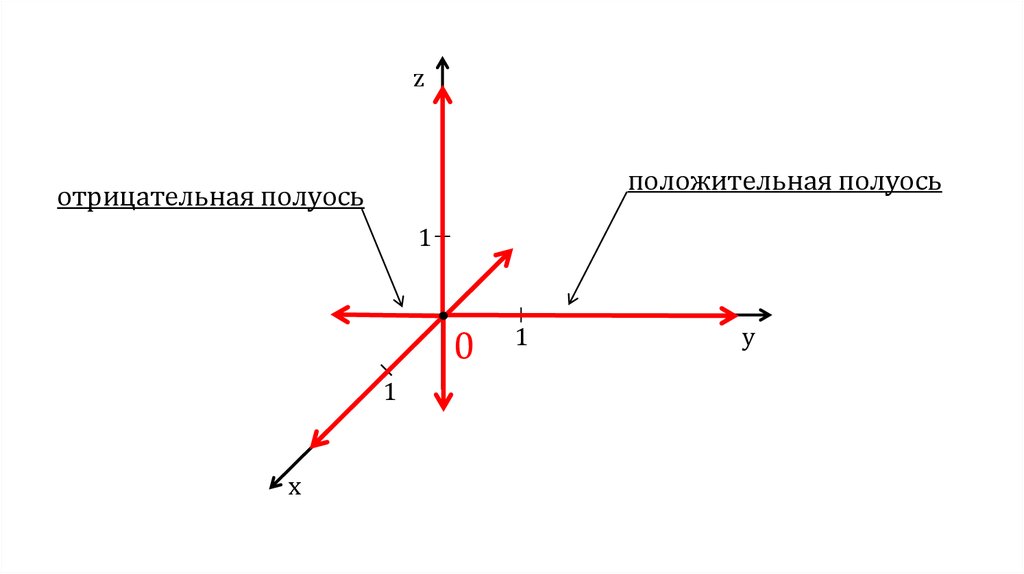
zположительная полуось
отрицательная полуось
1
0
1
x
1
y
7.
zМ(х;у;z)
M
1
0
1
y
1
x
Запомните! Первой указывают абсциссу (х), второй –
ординату (у), третьей — аппликату (z).
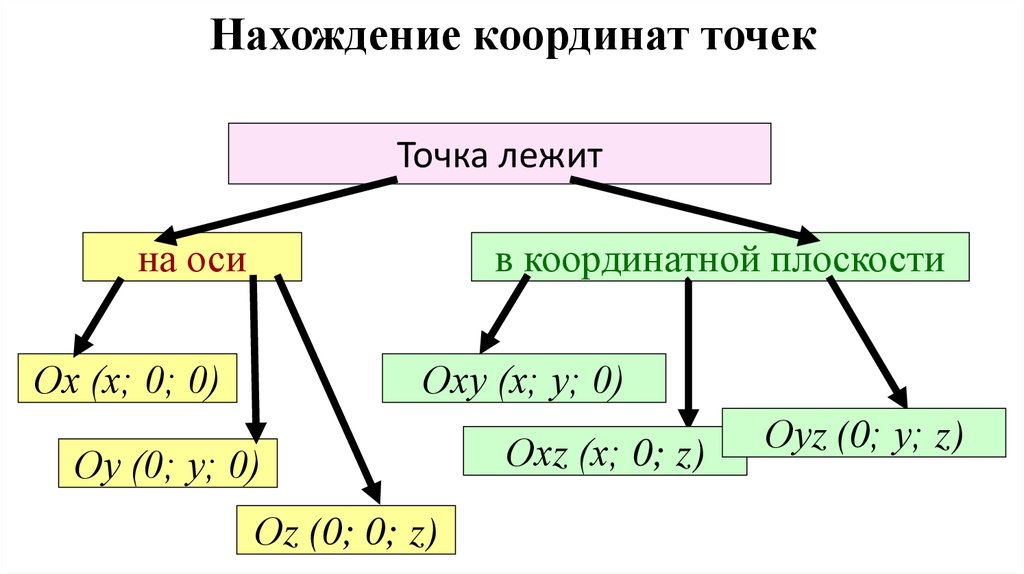
8. Нахождение координат точек
Точка лежитна оси
в координатной плоскости
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)
9.
Даны точки:А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
D (-4; -1; 0)
Е (0; -3; 0)
F (1; 2; 3)
Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz
Назовите точки, лежащие
в плоскости Охz
Назовите точки, лежащие
в плоскости Оху
10.
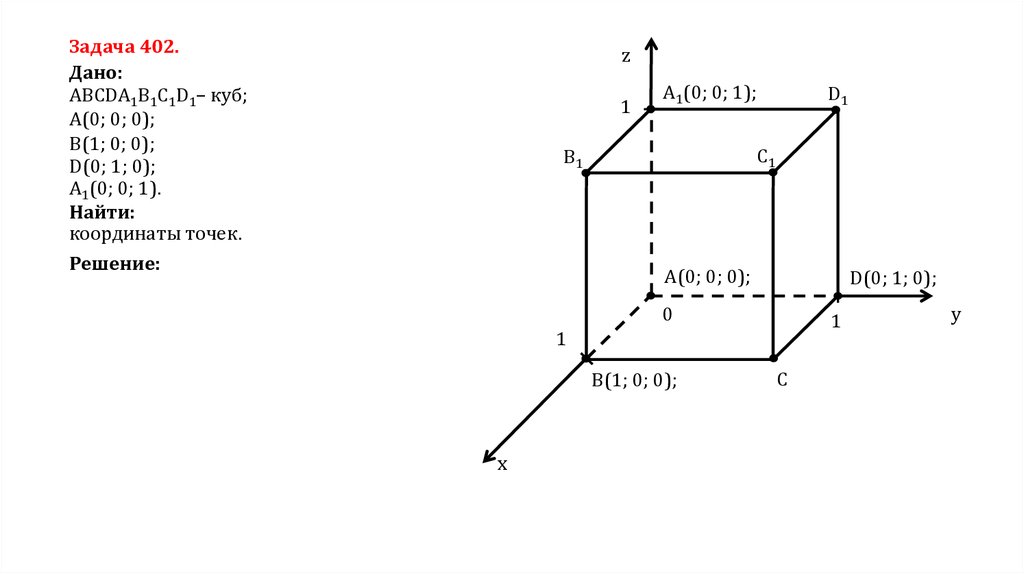
Задача 402.Дано:
ABCDA1B1C1D1– куб;
A(0; 0; 0);
B(1; 0; 0);
D(0; 1; 0);
A1(0; 0; 1).
Найти:
координаты точек.
Решение:
z
1
A1(0; 0; 1);
D1
C1
B1
A(0; 0; 0);
D(0; 1; 0);
0
1
1
B(1; 0; 0);
x
C
y
11. Координаты вектора
12. Правила действий над векторами с заданными координатами
1. Равные векторы имеют равные координатыПусть
а х1 ; у1 ; z1
b х2 ; у2 ; z2
, тогда
a b
х1 = х2; у1 = у2; z1 = z2
13.
2. Каждаякоордината суммы двух (и более)
векторов равна сумме соответствующих
координат этих векторов
а х1; у1; z1
b х2 ; у2 ; z 2
с a b
Следовательно с х1 х2 ; у1 у2 ; z1 z 2
14.
3. Каждая координата произведения вектора начисло равна произведению соответствующей
координаты на это число.
4. Каждая координата разности двух векторов
равна разности соответствующих координат
на этих векторов.
а х1 ; у1 ; z1
b х2 ; у2 ; z2
с a b
с х1 х2 ; у1 у2 ; z1 z 2
15. Выполнить задание устно:
• Даны векторы:а 3;5; 7
b 4; 1;3
c 0;1;8
• Найти вектор равный:
а) 2 а 2 а 6;10; 14 б ) 3 b
в) a b
a b 7;4; 4
г) b с
b с 4; 2; 5
д) а b d
d 3;0;0
3 b 12;3; 9
e) 3d 2c
а b d 10;4; 4
3d 2c 9; 2; 8
16. Основные формулы:
1. Координаты вектораA( x1, y1, z1 )
B( x2 , y2 , z2 )
AB{x2 x1; y2 y1; z2 z1}
2. Длина вектора
AB{x; y; z}
AB x 2 y 2 z 2
17.
3. Расстояние между двумя точкамиA( x1, y1, z1 )
B( x2 , y2 , z2 )
d ( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2
4. Нахождение координаты середины С(x;y;z) отрезка АВ
A( x1, y1, z1 )
x
x1 x2
2
B( x2 , y2 , z2 )
y
y1 y2
2
z
z1 z 2
2
18.
5. Скалярное произведение векторовab a b cos( ab)
Скалярное произведение ненулевых векторов равно нулю тогда и только
тогда, когда эти вектора перпендикулярны.
a{x1 , y1 , z1}
b{x2 , y2 , z2 }
ab x1 x2 y1 y2 z1 z2
19.
6. Косинус угла между векторамиa{x1 , y1 , z1}
cos
b{x2 , y2 , z2 }
x1 x2 y1 y2 z1 z 2
x12 y12 z12 x22 y22 z 22
7. Косинус угла между плоскостями
cos
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
20.
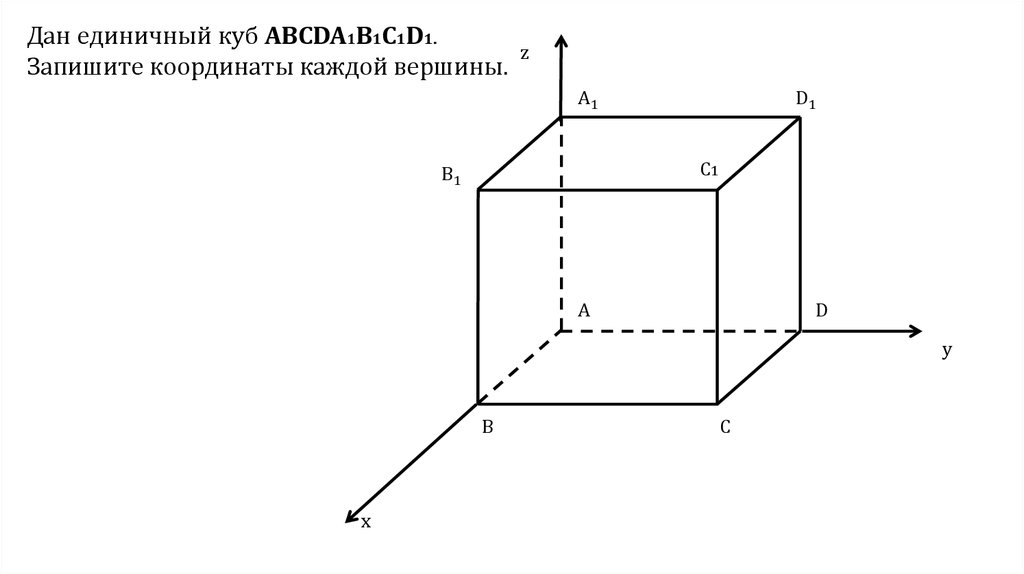
Дан единичный куб ABCDA1B1C1D1.Запишите координаты каждой вершины.
z
A1
D1
C1
B1
A
D
y
B
x
C
21.
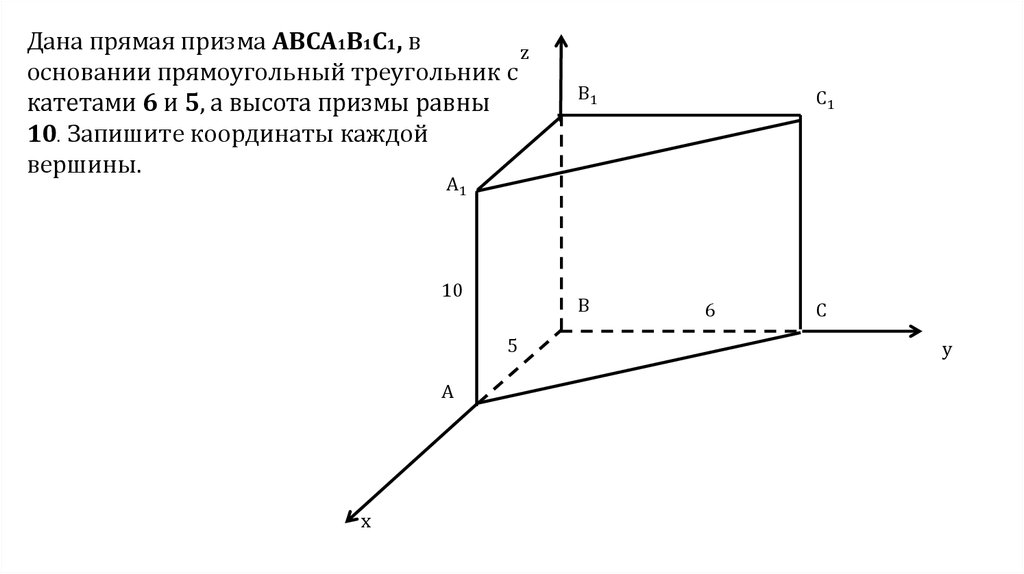
Дана прямая призма ABCA1B1C1, вz
основании прямоугольный треугольник с
катетами 6 и 5, а высота призмы равны
10. Запишите координаты каждой
вершины.
B1
C1
A1
10
B
5
A
x
6
C
y
22.
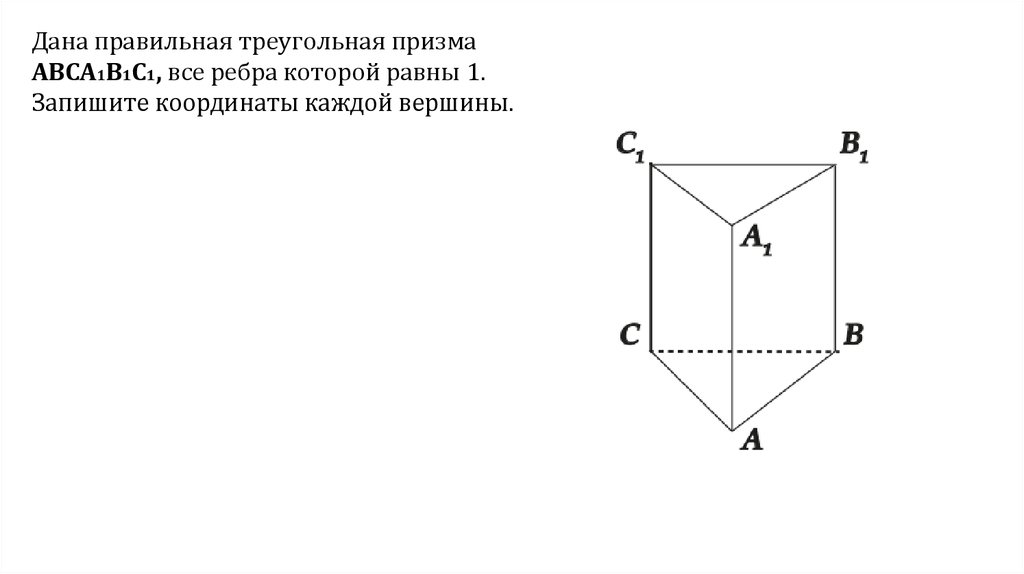
Дана правильная треугольная призмаABCA1B1C1, все ребра которой равны 1.
Запишите координаты каждой вершины.
23.
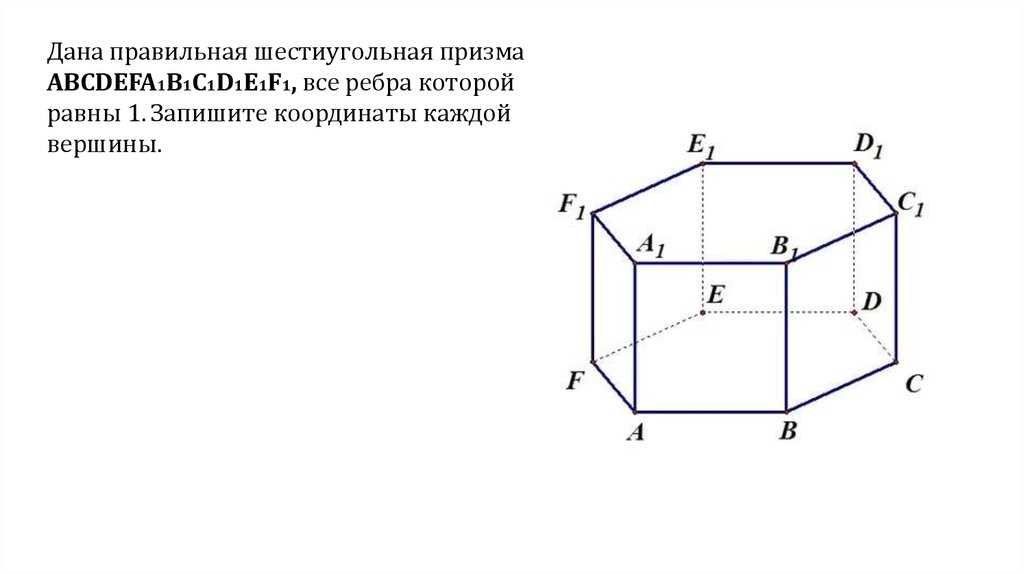
Дана правильная шестиугольная призмаABCDEFA1B1C1D1E1F1, все ребра которой
равны 1. Запишите координаты каждой
вершины.
24.
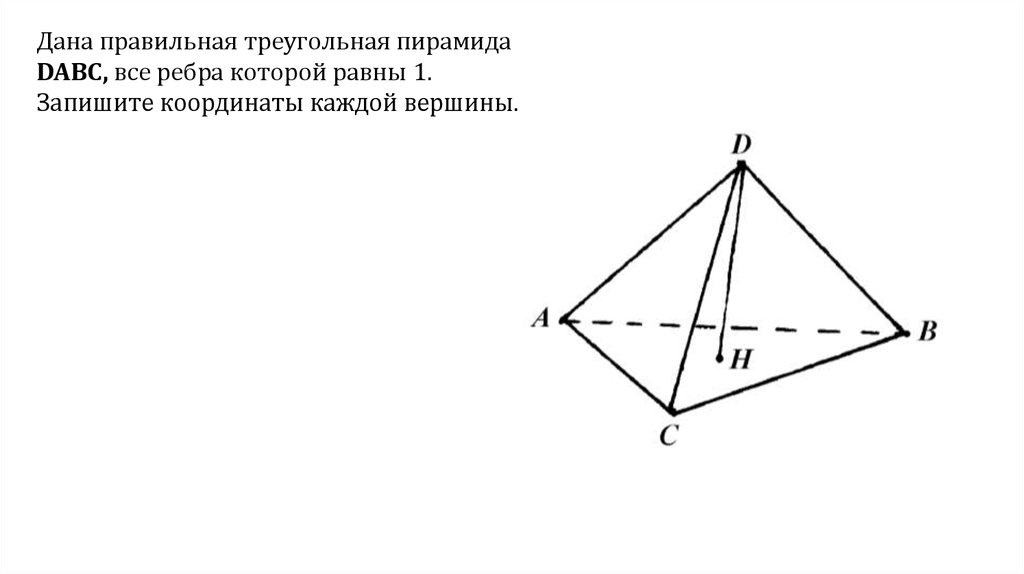
Дана правильная треугольная пирамидаDABC, все ребра которой равны 1.
Запишите координаты каждой вершины.
25.
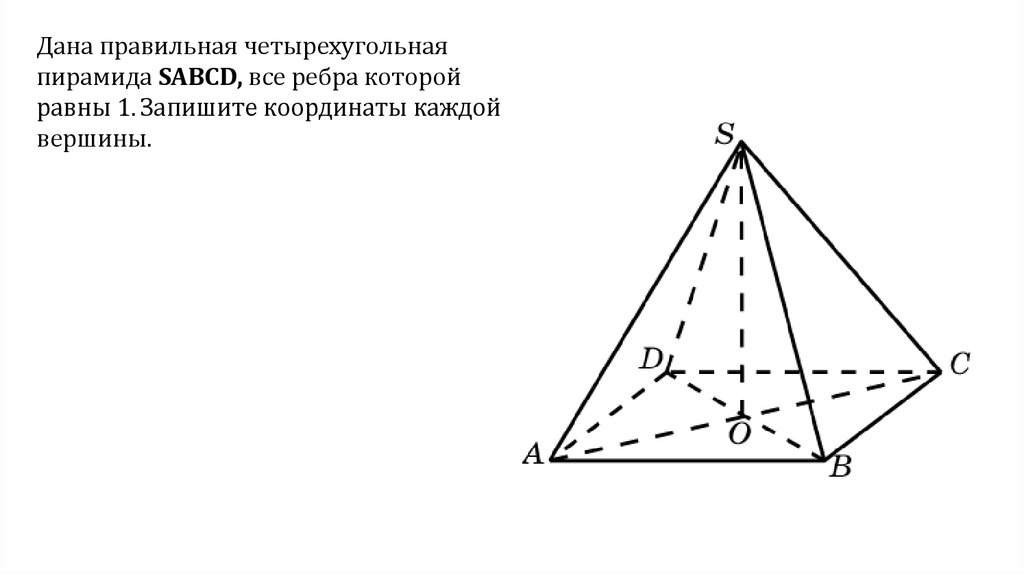
Дана правильная четырехугольнаяпирамида SABCD, все ребра которой
равны 1. Запишите координаты каждой
вершины.
26.
Дана правильная шестиугольнаяпирамида SABCDEF, стороны основания
которого равны 1, боковые ребра 2.
Запишите координаты каждой вершины.















 mathematics
mathematics