Similar presentations:
Связанные волны в нелинейной среде
1.
Связанные волны в нелинейной средеЛекция 3-4
Нелинейная оптика
Система связанных уравнений для трехволнового процесса примет вид:
2.
Перестановочная симметрия восприимчивостиДля действительности электромагнитного поля нужно ввести
отрицательные частоты
E(r, t ) E (r )e i t E (r ) ei t
D(r, t ) ( )E (r )e i t ( )E (r ) ei t
для диэлектрической проницаемости верно соотношение
Лекция 3-4
Нелинейная оптика
тогда вектор электрической индукции
( ) ( )
для линейной восприимчивости
ij(1) ( ) ij(1) ( )
что трактуется как частный случай принципа обратимости Онзагера
! NB Поговорить
- про соотношения Крамерса-Кронига
- про комплексность линейной
восприимчивости
- про комплексность нелинейной
восприимчивости
3.
Перестановочная симметрия восприимчивостиДля нелинейной (например, квадратичной) восприимчивости
перестановочные соотношения аналогичны:
(2)
(2)
ijk
( 1 2 3 ) (2)
(
)
2
3
1
jki
kij ( 3 1 2 )
Лекция 3-4
Нелинейная оптика
(обратить внимание на вращение декартовых индексов)
В полосе прозрачности, где дисперсией можно пренебречь,
перестановочная симметрия становится частотно независимой
(соотношения Клейнмана) – можно вращать индексы не вращая частоты
! NB Поговорить
- 27 10
- 27 18 - SHG
Можно ввести эмпирические коэффициенты Миллера:
ijk
(2)
ijk
( 1 2 3 )
(1)
ii(1) ( 1 ) (1)
(
)
jj
2
kk ( 3 )
которые являются константами в широком спектральном диапазоне
4.
ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ КРИСТАЛЛАось симметрии n=3
_
центр инверсии 1
Лекция 3-4
Нелинейная оптика
ЭЛЕМЕНТЫ СИММЕТРИИ
= 2 /n
n = 1,2,3,4,6
_
1=
{
2/m
4/m
6/m
5.
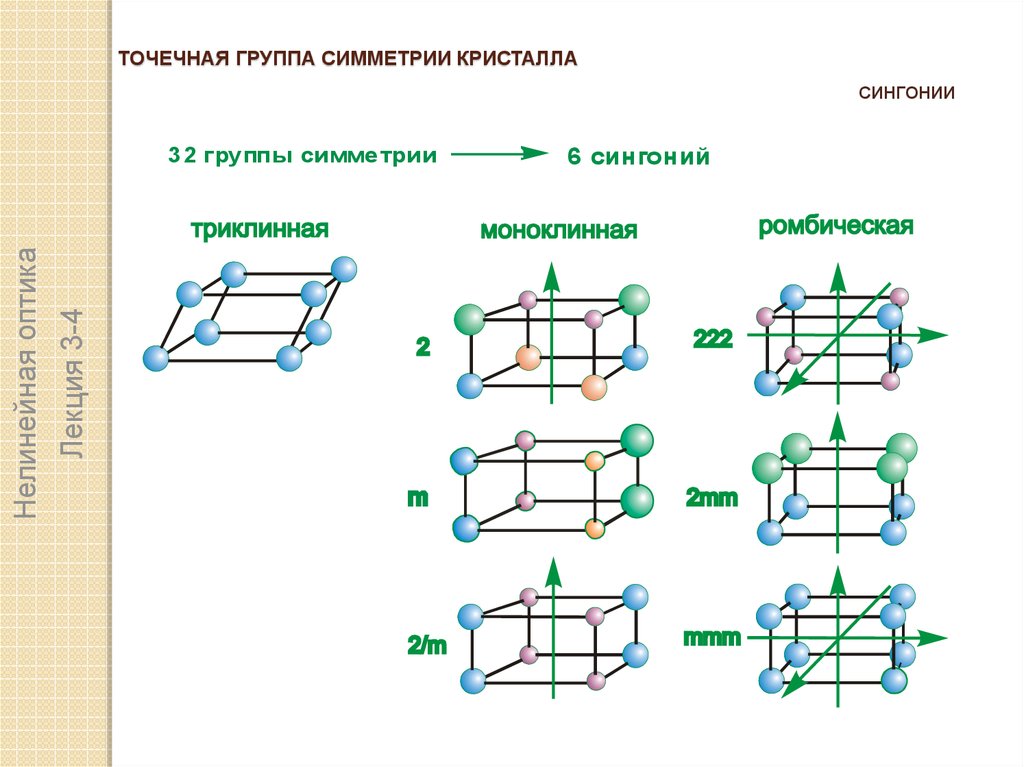
ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ КРИСТАЛЛАСИНГОНИИ
Лекция 3-4
Нелинейная оптика
3 2 гру ппы симме трии
6 сингоний
6.
ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ КРИСТАЛЛАЛекция 3-4
Нелинейная оптика
СИНГОНИИ
7.
ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ КРИСТАЛЛАЛекция 3-4
Нелинейная оптика
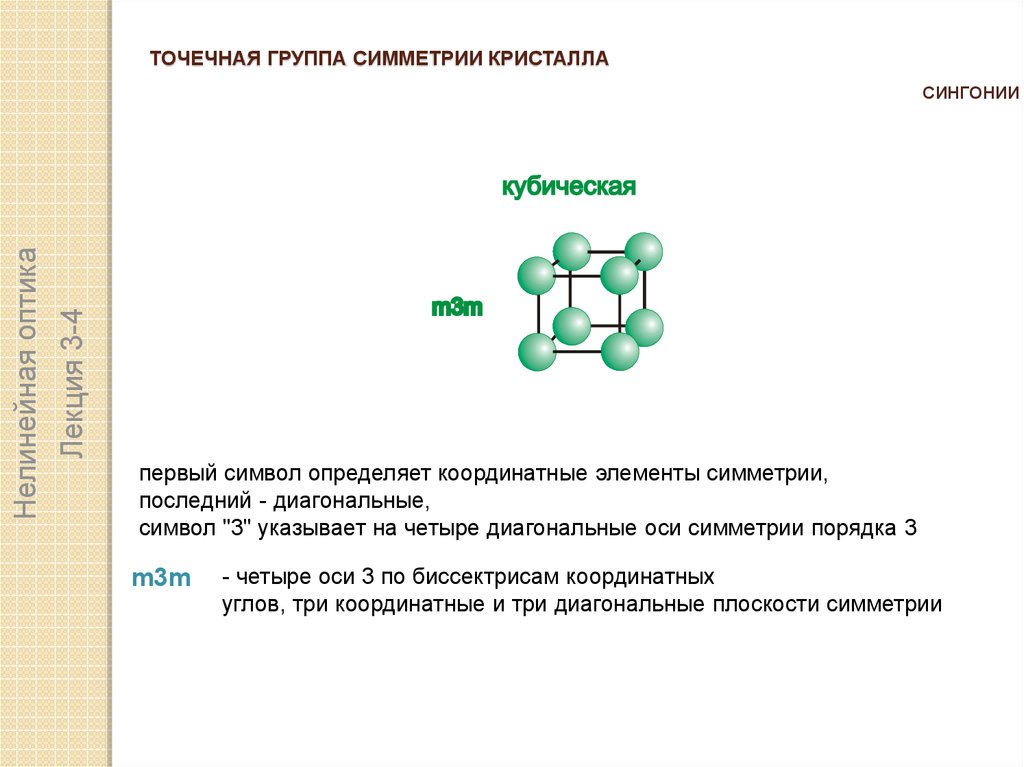
СИНГОНИИ
первый символ определяет координатные элементы симметрии,
последний - диагональные,
символ "3" указывает на четыре диагональные оси симметрии порядка 3
m3m
- четыре оси 3 по биссектрисам координатных
углов, три координатные и три диагональные плоскости симметрии
8.
ТОЧЕЧНАЯ ГРУППА СИММЕТРИИ КРИСТАЛЛАЛекция 3-4
Нелинейная оптика
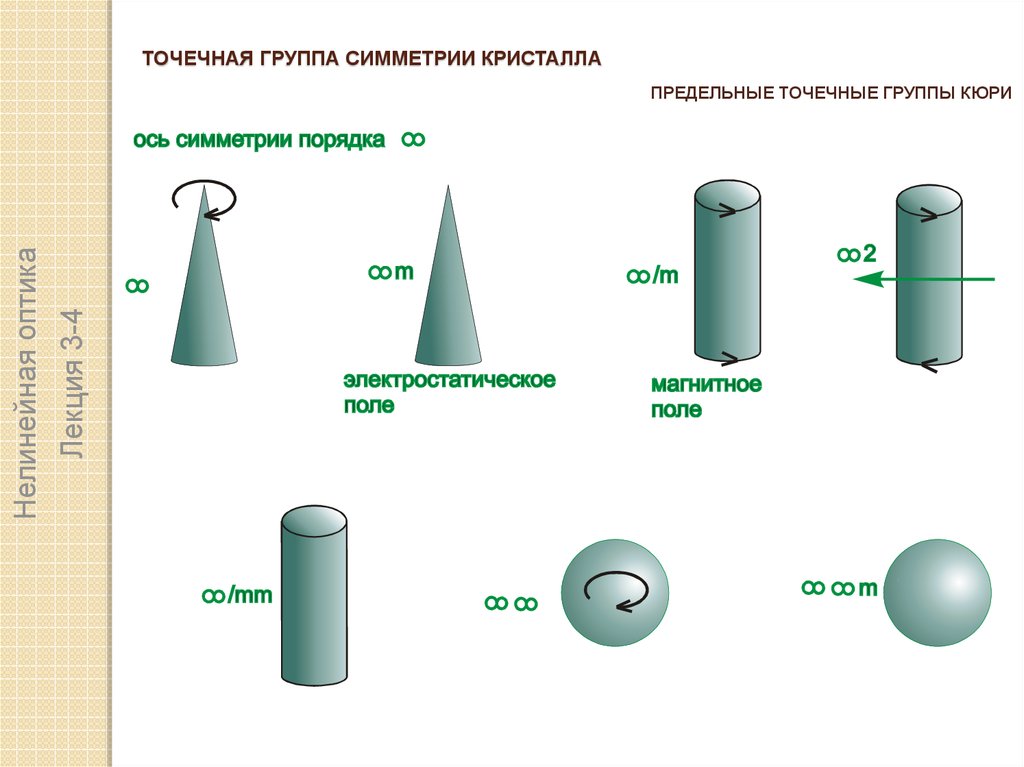
ПРЕДЕЛЬНЫЕ ТОЧЕЧНЫЕ ГРУППЫ КЮРИ
9.
КВАДРАТИЧНАЯ ВОСПРИИМЧИВОСТЬ И СИММЕТРИЯ КРИСТАЛЛА(n)
xi
- координаты в кристаллографической системе координат
(для кристаллов кубической сингонии - ортонормированные
декартовы координаты)
- тензор преобразования координат операции симметрии кристалла
закон преобразования координат операции симметрии кристалла:
Лекция 3-4
Нелинейная оптика
Tij
- тензор нелинейной восприимчивости порядка n
xi Tij x j
закон преобразования компонент
( n)
при действии операции симметрии кристалла:
(2)
(2)
ijk
Til TjmTkn lmn
потребуем инвариантности нелинейной восприимчивости по отношению ко всем
операциям симметрии точечной группы кристалла:
(2)
(2)
ijk
il jm kn lmn
получим систему линейных уравнений для компонент тензора нелинейной
восприимчивости:
2)
(Til TjmTkn il jm kn) (lmn
0
10.
КВАДРАТИЧНАЯ ВОСПРИИМЧИВОСТЬ ОБЪЕМА И ПОВЕРХНОСТИЦЕНТРОСИММЕТРИЧНЫХ СРЕД
в кристаллах с инверсной симметрией
тогда уравнение
2)
(Til TjmTkn il jm kn) (lmn
0
преобразуется в
( 2)
( 2)
ijk
ijk
(2)
ijk
0
- симметрийный запрет на четные нелинейно-оптические эффекты в кристаллах с инверсной
симметрией в дипольном приближении
Лекция 3-4
Нелинейная оптика
таким образом
T
(2) Surface
ijk
0
нарушение инверсной симметрии на поверхности
поверхность (111)
симметрия 3m
поверхность (011)
симметрия 2mm
поверхность (001)
симметрия 4m
Z [001]
X [100]
Y [010]
Z [1 1 1]
Z [0 1 1]
X [1 0 0]
Y [0 1 -1]
Y [0 1 -1]
а)
m3m,
4m
б)
2m
X [2 -1 -1]
в)
3m
11.
Энергия поля в нелинейной средеЛекция 3-4
Нелинейная оптика
Из уравнений Максвелла можно получить, что
скорость истечения энергии из единицы объема равна скорости убыли
плотности запасенной в нем электромагнитной энергии
Записав полную поляризацию среды в виде
можно ввести мгновенную плотность энергии электромагнитной
волны в нелинейной среде:
12.
Энергия поля в нелинейной средеможно записать в виде
Лекция 3-4
Нелинейная оптика
Тогда соотношение
Усредненное по времени выражение будет выражать закон
сохранения энергии в нелинейной среде:
с
E B U
4
t









 physics
physics








