Similar presentations:
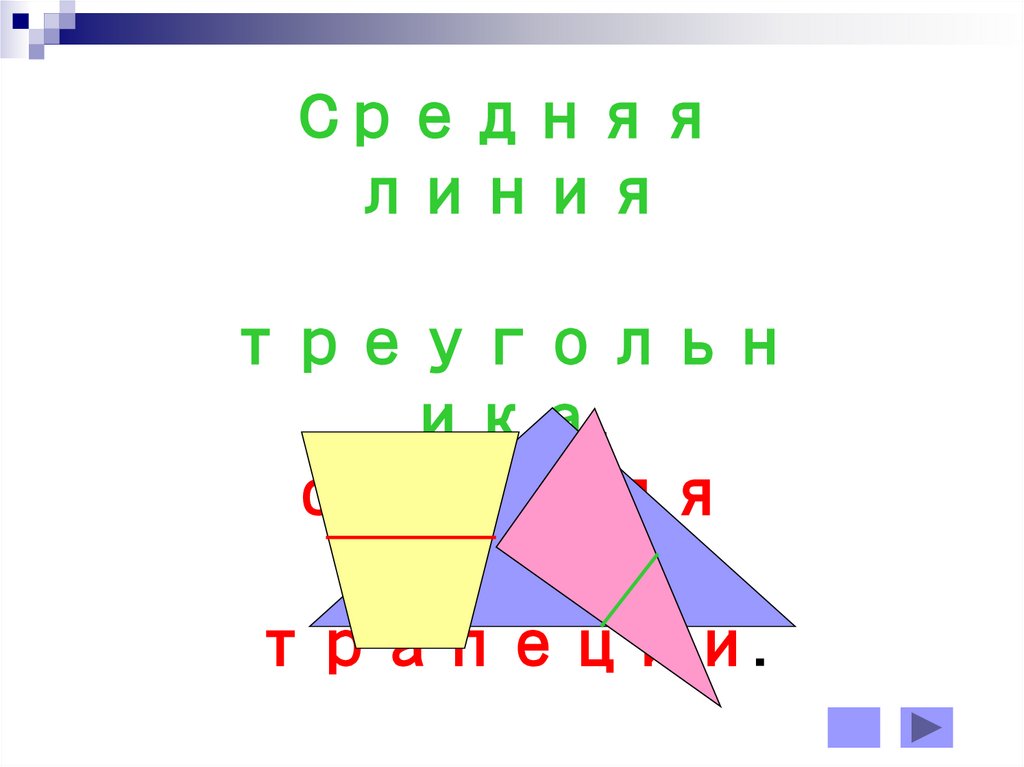
Cредняя линия треугольника, средняя линия трапеции
1.
Cредняялиния
треугольн
ика,
средняя
линия
трапеции.
2.
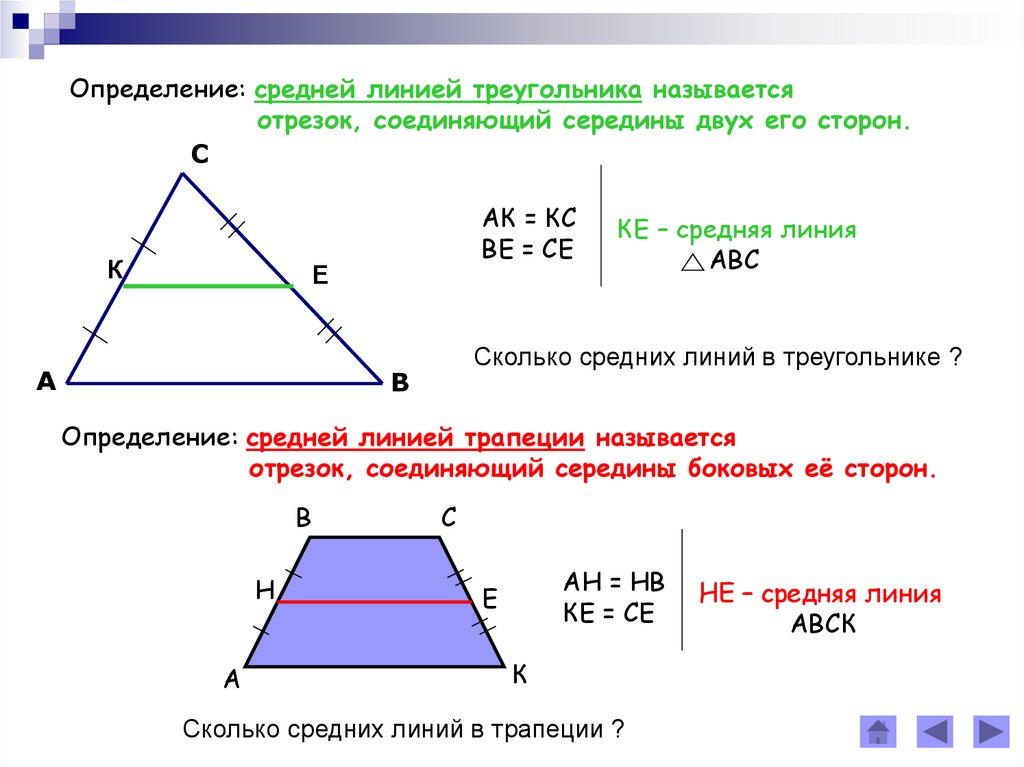
Определение: средней линией треугольника называетсяотрезок, соединяющий середины двух его сторон.
С
К
АК = КС
ВЕ = СЕ
Е
А
КЕ – средняя линия
АВС
Сколько средних линий в треугольнике ?
В
Определение: средней линией трапеции называется
отрезок, соединяющий середины боковых её сторон.
В
Н
А
С
АН = НВ
КЕ = СЕ
Е
К
Сколько средних линий в трапеции ?
НЕ – средняя линия
АВСК
3.
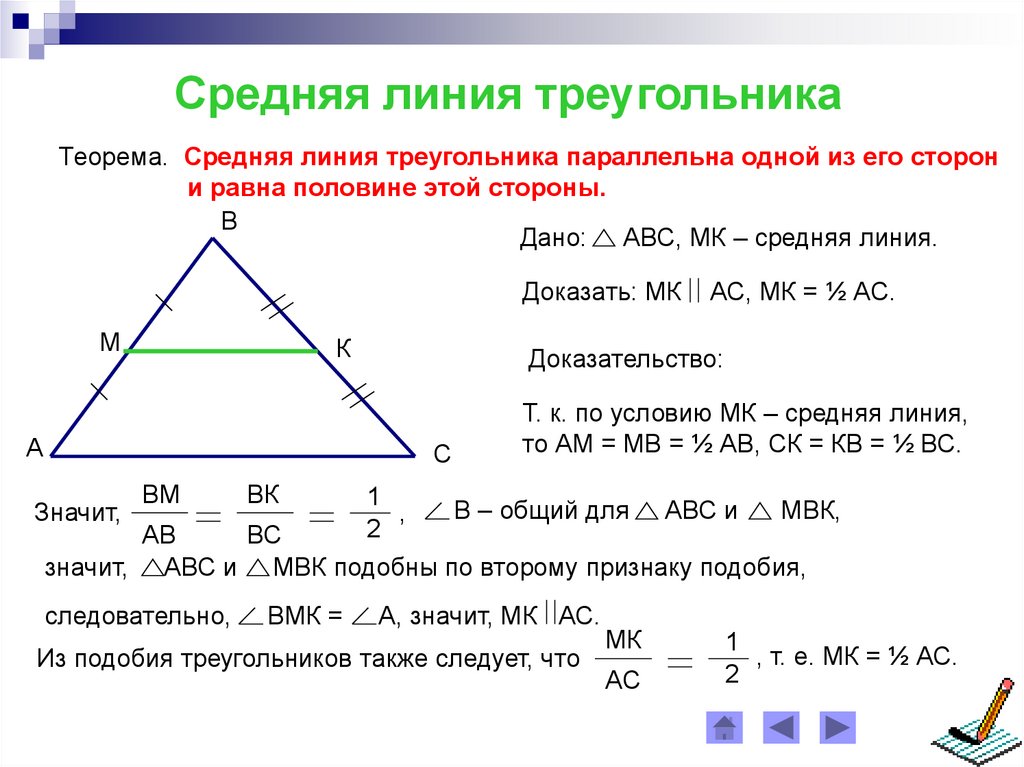
Средняя линия треугольникаТеорема. Средняя линия треугольника параллельна одной из его сторон
и равна половине этой стороны.
В
Дано: АВС, МК – средняя линия.
Доказать: МК
М
К
А
Доказательство:
С
ВМ
АС, МК = ½ АС.
Т. к. по условию МК – средняя линия,
то АМ = МВ = ½ АВ, СК = КВ = ½ ВС.
ВК
1
В – общий для АВС и
МВК,
,
2
АВ
ВС
значит, АВС и МВК подобны по второму признаку подобия,
Значит,
следовательно,
ВМК =
А, значит, МК АС.
Из подобия треугольников также следует, что
МК
АС
1
, т. е. МК = ½ АС.
2
4.
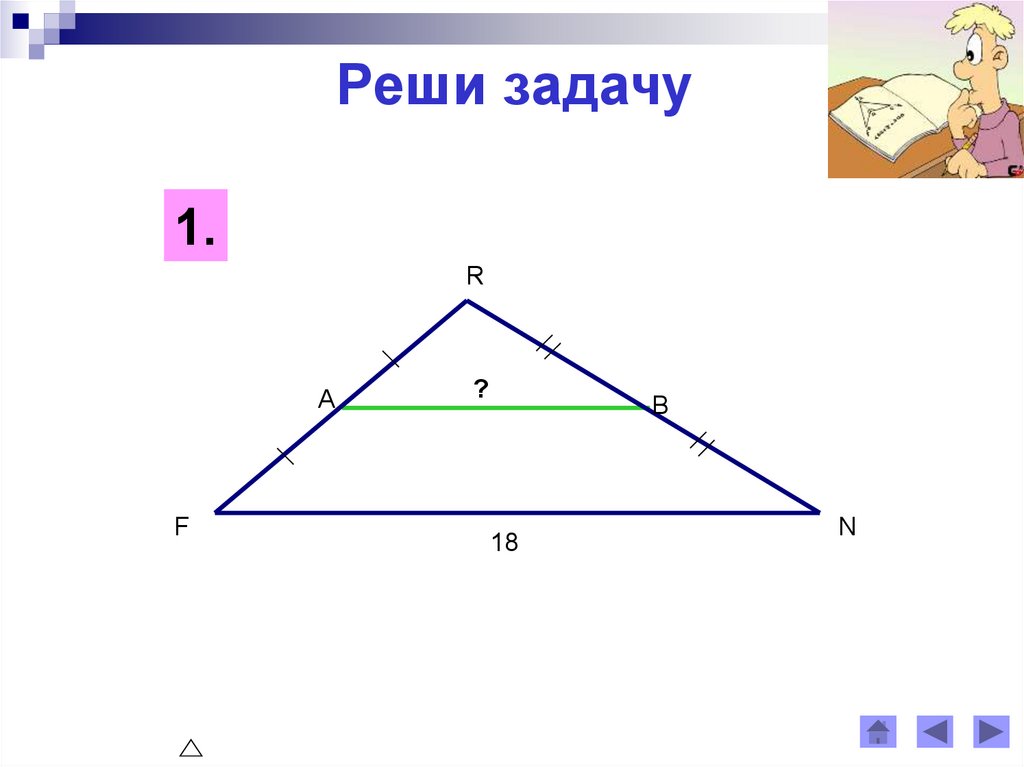
Реши задачу1.
R
А
F
?
В
18
N
5.
Реши задачу2.
С
К
?
В
2,7
М
А
6.
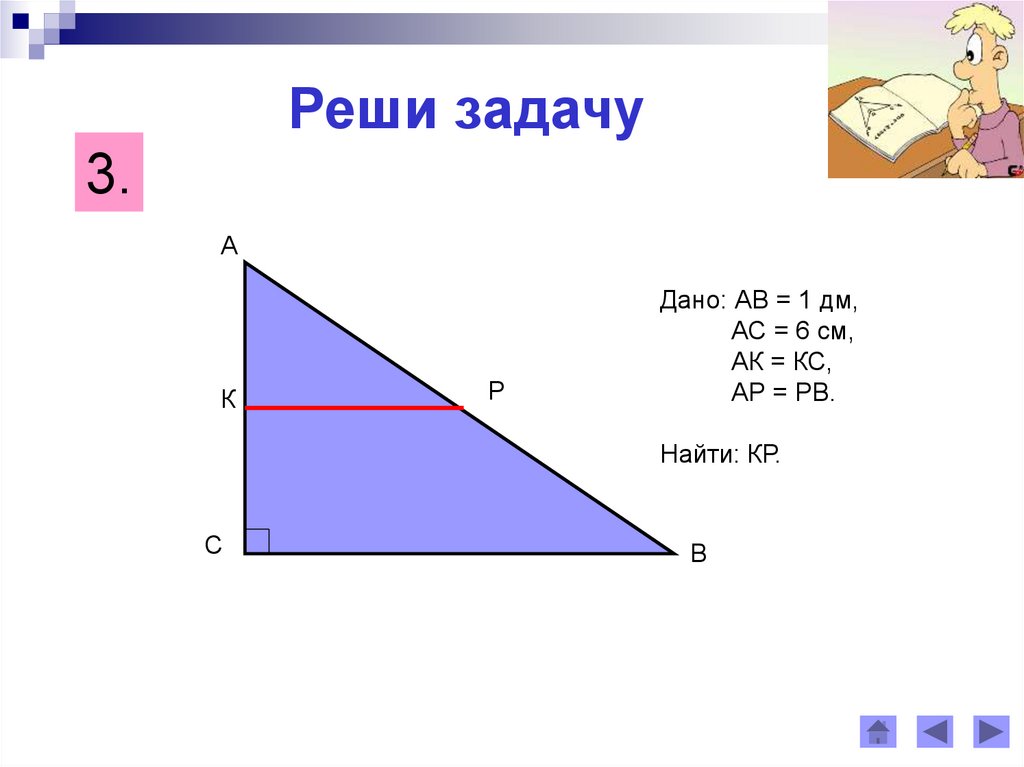
Реши задачу3.
А
К
Р
Дано: АВ = 1 дм,
АС = 6 см,
АК = КС,
АР = РВ.
Найти: КР.
С
В
7.
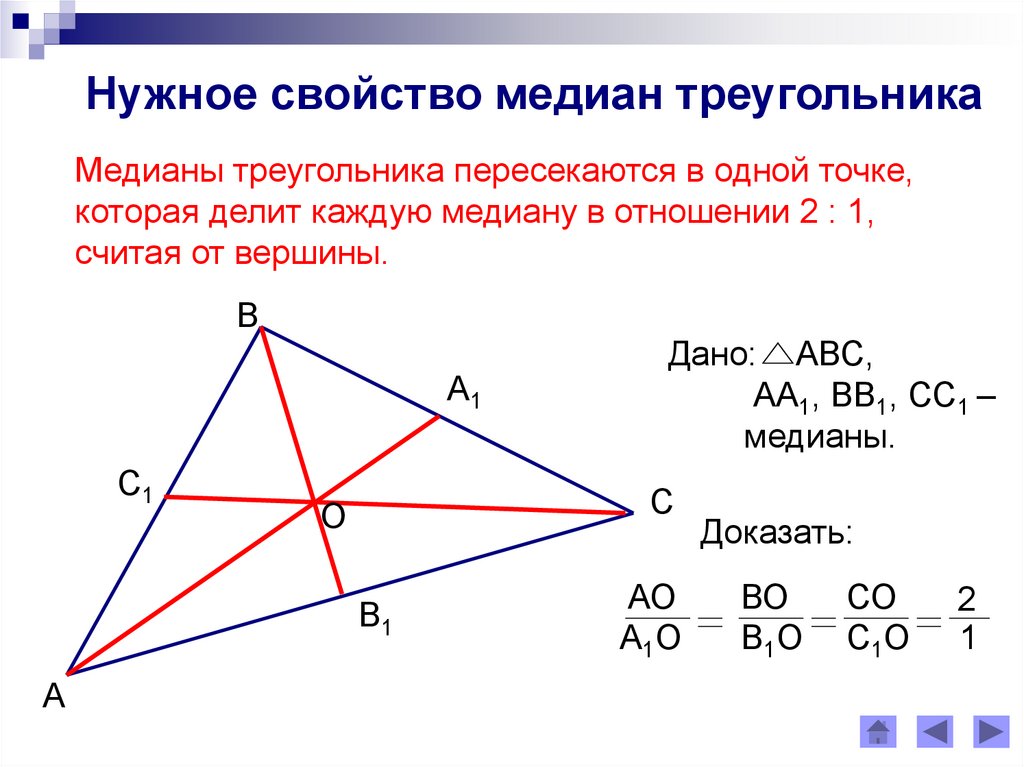
Нужное свойство медиан треугольникаМедианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2 : 1,
считая от вершины.
В
А1
С1
С
О
В1
А
Дано: АВС,
АА1, ВВ1, СС1 –
медианы.
АО
А1О
Доказать:
ВО
В1О
СО
С1О
2
1
8.
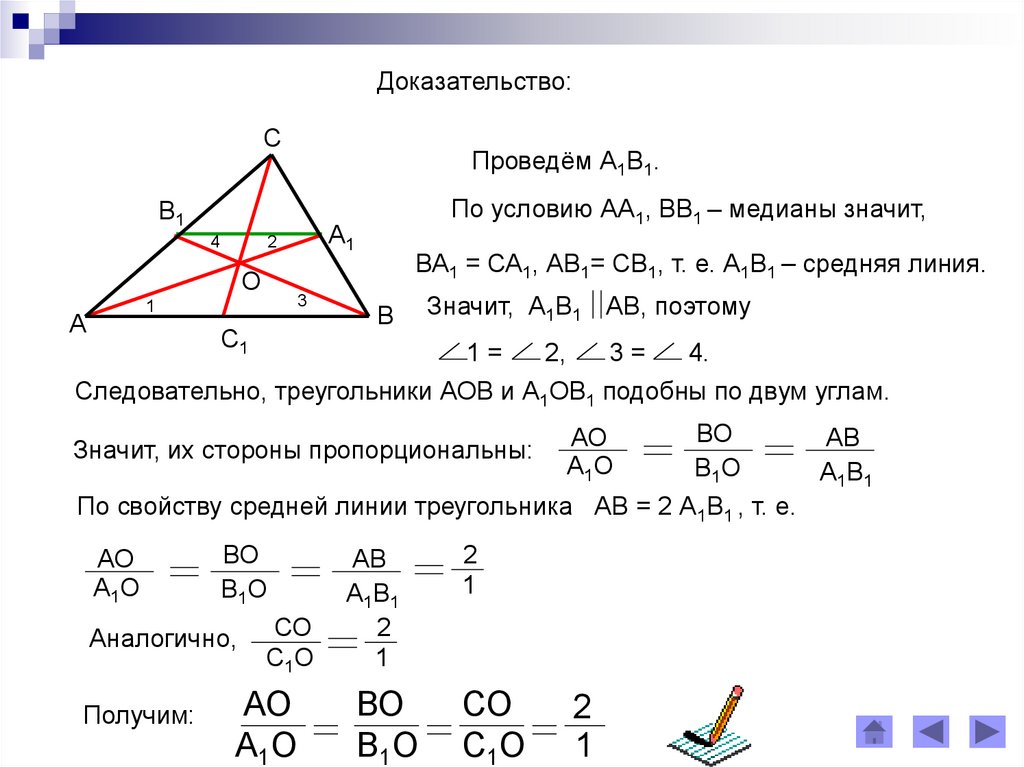
Доказательство:С
Проведём А1В1.
В1
4
3
1
А
А1
2
О
По условию АА1, ВВ1 – медианы значит,
С1
ВА1 = СА1, АВ1= СВ1, т. е. А1В1 – средняя линия.
В
Значит, А1В1 АВ, поэтому
1=
2,
3=
4.
Следовательно, треугольники АОВ и А1ОВ1 подобны по двум углам.
Значит, их стороны пропорциональны:
АО
А1О
ВО
В1О
По свойству средней линии треугольника АВ = 2 А1В1 , т. е.
АО
А1О
ВО
В1О
Аналогично,
Получим:
СО
С1О
АО
А1О
АВ
А1В1
2
1
ВО
В1О
2
1
СО
С1О
2
1
АВ
А1В1
9.
Средняя линия трапецииТеорема. Средняя линия трапеции параллельна основаниям
и равна их полусумме.
В
Дано: АВСК – трапеция,
МР – средняя линия.
С
Р
М
Е
Доказать: МР
АК, МР
О
МР =
К
А
Проведём через точку М прямую МЕ
Т. к. АВСК – трапеция, то ВС
Доказательство:
AK BC
2
АК, докажем, что МЕ пройдёт через Р.
АК, а, значит, ВС
МЕ
АК.
Т. к. МР – средняя линия, то АМ= МВ, КР = СР.
Следовательно, МР лежит на МЕ, значит, МР АК, МР ВС.
Проведём ВК. По теореме Фалеса О – середина ВК, значит,
МО – средняя линия
ВС,
АВК, ОР – средняя линия
ВСК.
AK BC
МР = МО + ОР = ½ АК + ½ ВС = ½ ( АК + ВС) =
2
По теореме Фалеса
МЕ пересечёт СК
в середине СК,
т. е. в точке Р.
10.
Реши задачуНайти длину средней линии ОЕ трапеции АВСК
по данным на чертеже:
В
7
О
А
С
Е
15
К
11.
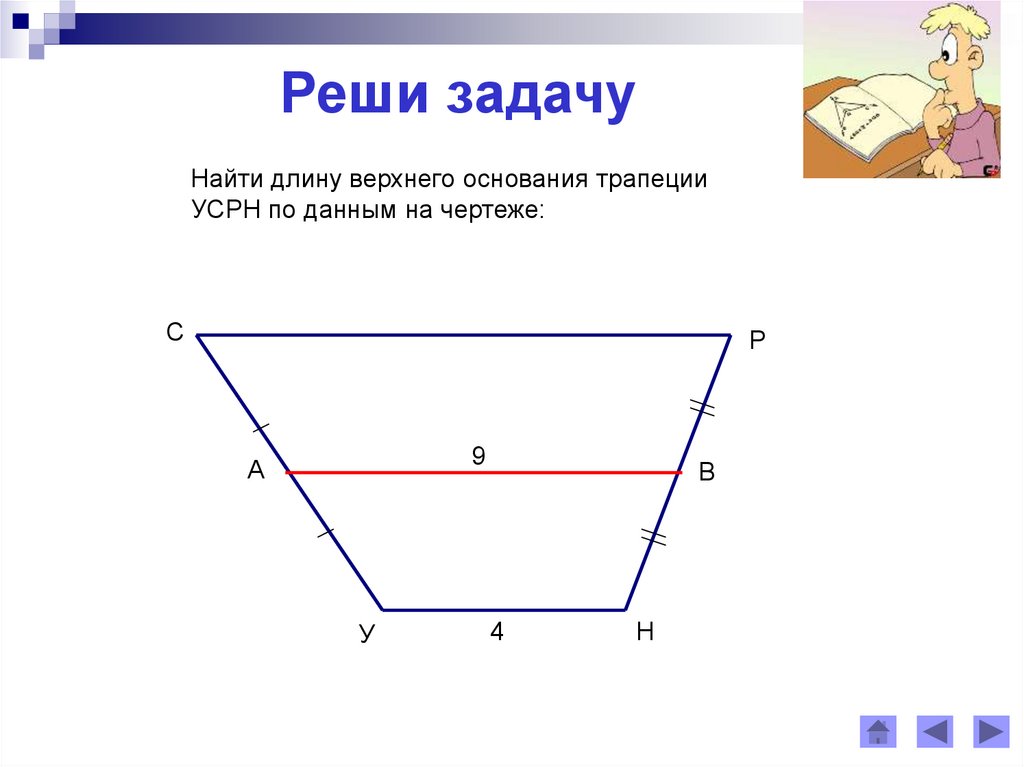
Реши задачуНайти длину верхнего основания трапеции
УСРН по данным на чертеже:
С
Р
9
А
У
В
4
Н
12.
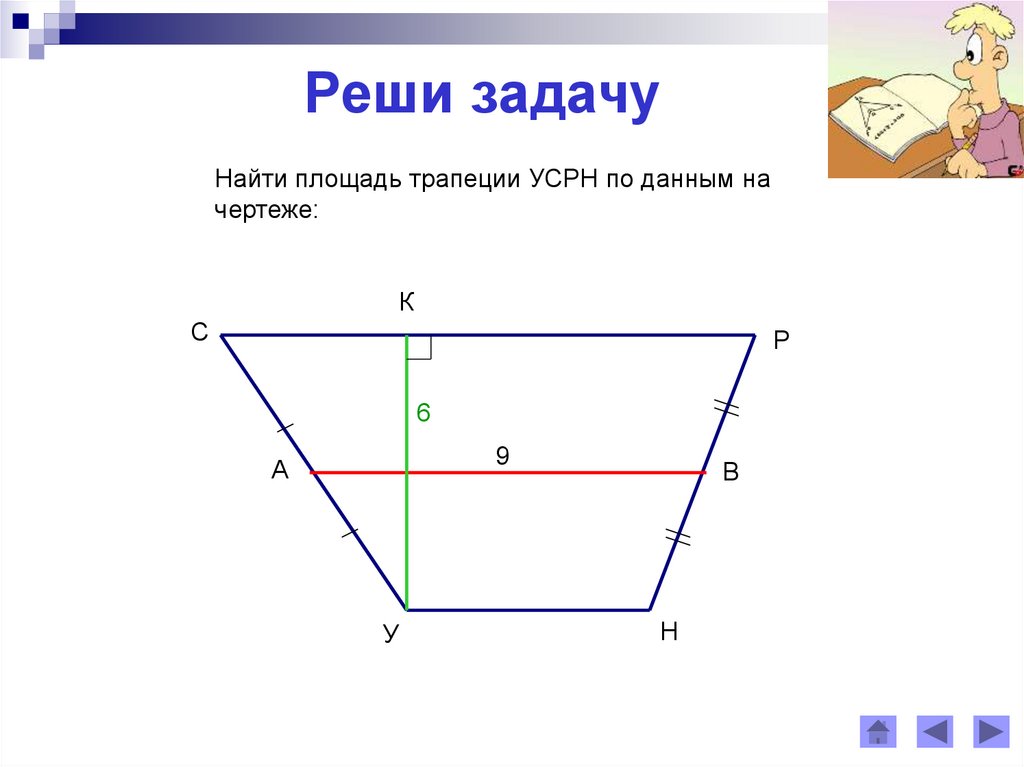
Реши задачуНайти площадь трапеции УСРН по данным на
чертеже:
К
С
Р
6
9
А
У
В
Н
13.
Решение задачиB ромбе АBСD О- точка пересечения диагоналей, Е и F - середины
сторон ВС и DС. Докажите, что ЕF = ВО, ЕF АС
Дано:
E
АВСD - ромб,
B
C
О– точка пересечения диагоналей,
Е - середина ВС,
F
F - середина DС.
O
Доказать:
ЕF = ВО, ЕF АС.
A
D
Доказательство:
Так как АВСD - ромб, то ВО = ОD = ½ ВD, ВD АС.
Рассмотрим ВСD. Так как Е–середина ВС, F - середина DС,
то ЕF- средняя линия ВСD,
значит, ЕF = ½ ВD, и, следовательно, ЕF = ВО.
Пo свойству средней линии треугольника: ЕF ВD,
a по доказанному ВD
АС, значит, и ЕF
АС, что и т. д.
14.
Михайлова Л. П.ГОУ ЦО № 173.





 mathematics
mathematics








