Средняя линия треугольника. Свойство медиан треугольника

1.

2.

Каким образом эти треугольники поделили на две группы?

3.

Определение. Средней линией треугольника называется
отрезок, соединяющий середины двух его сторон.
С
А
В
Сколько средних линий можно построить в треугольнике?

4.

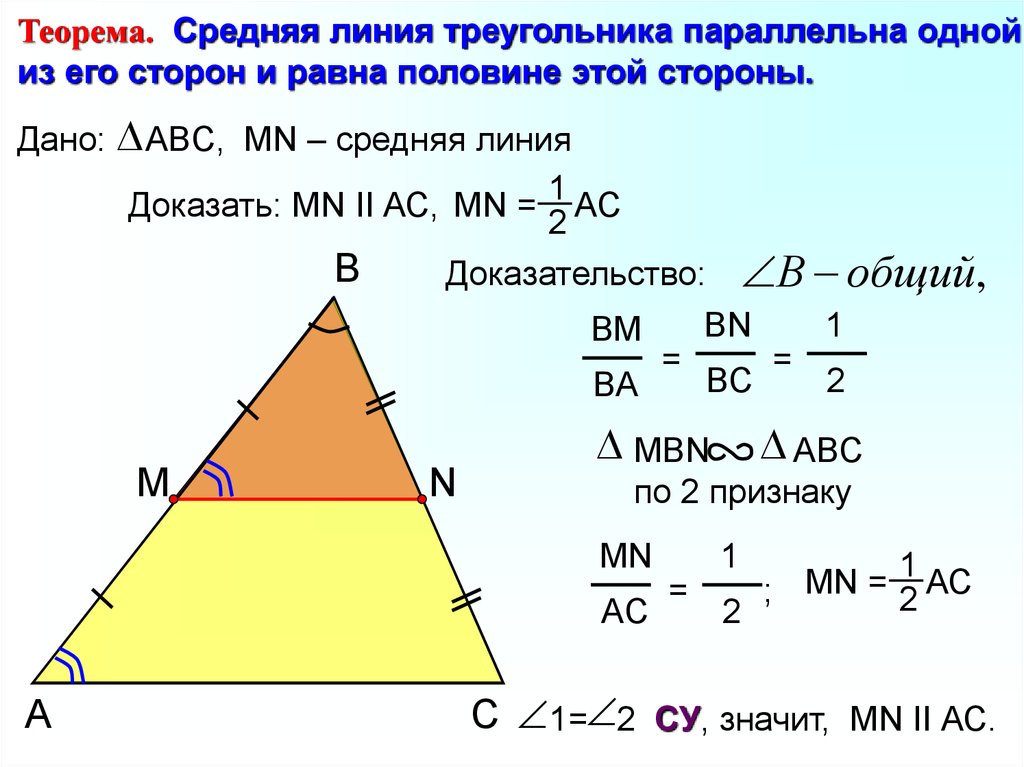
Теорема. Средняя линия треугольника параллельна одной
из его сторон и равна половине этой стороны.
Дано: ABC, МN – средняя линия
Доказать: МN II АС, MN = 1 АС
2
B
Доказательство: В общий,
BN
1
BM
=
=
BC
2
BA
М
N
MBN
ABC
по 2 признаку
MN
1
1 АС
MN
=
=
;
2
AC
2
А
C 1= 2 CУ, значит, МN II АС.

5.

Какую сторону треугольника АВС можно найти?
С
N
F
7 см
14
В
А
O

6.

Найдите стороны треугольника АВС.
С
F
16
8 см
7 см
14
5,5см
11
А
N
В
O

7.

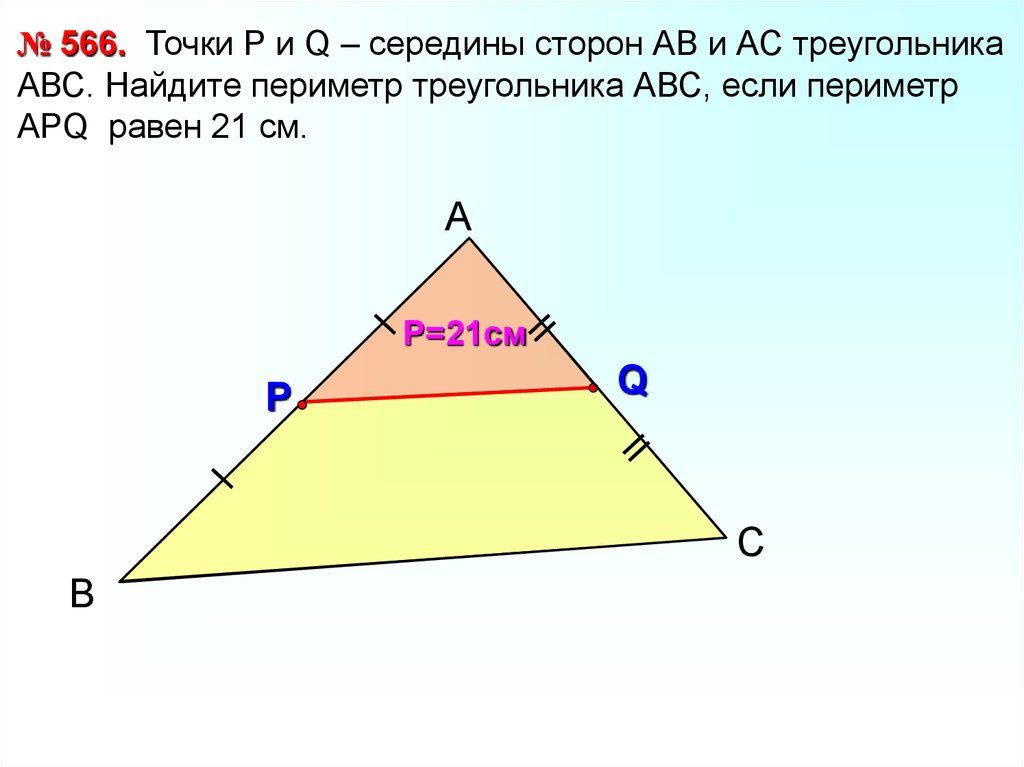
№ 566. Точки Р и Q – середины сторон АВ и АС треугольника
АВС. Найдите периметр треугольника АВС, если периметр
АРQ равен 21 см.
А
Р=21см
Р
Q
С
В

8.

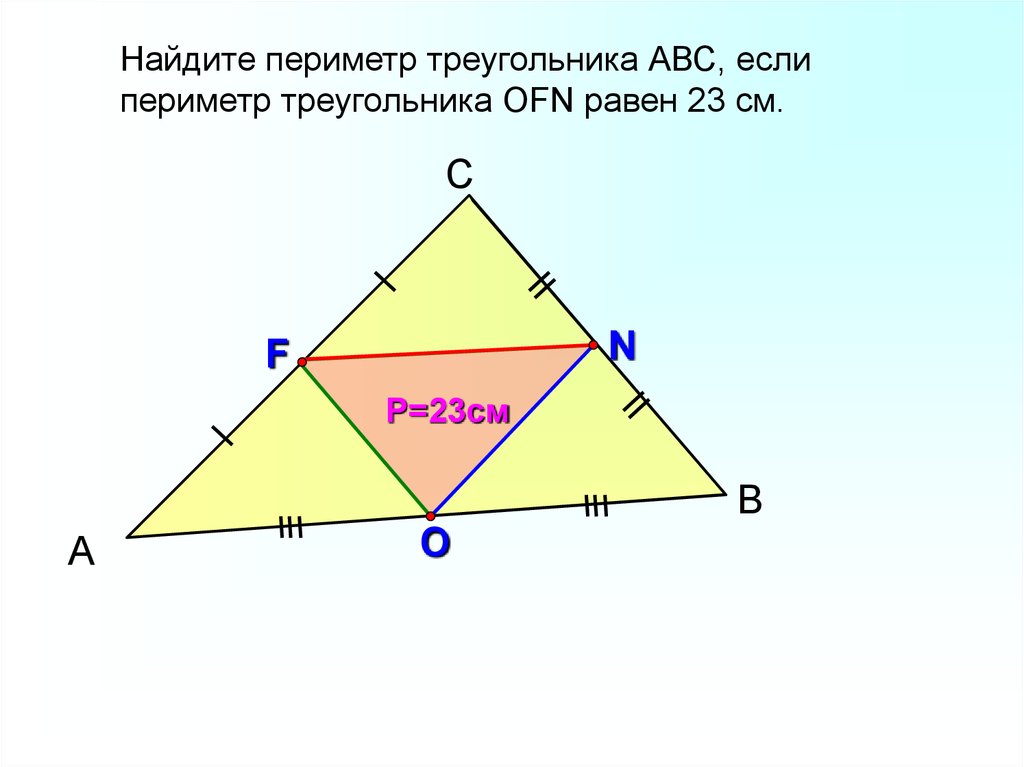
Найдите периметр треугольника АВС, если
периметр треугольника ОFN равен 23 см.
С
N
F
Р=23см
В
А
O

9.

Блиц-опрос
Найдите х, у, РАВС.
В
x10
6
М
А
N
8
y
16
С

10.

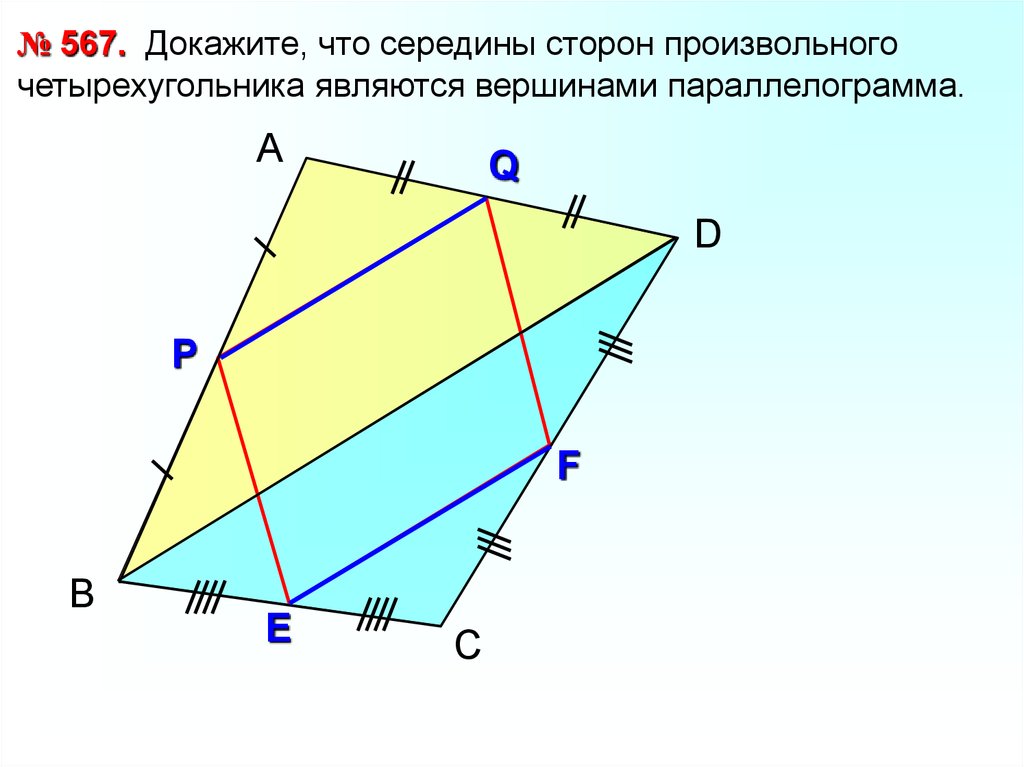
№ 567. Докажите, что середины сторон произвольного
четырехугольника являются вершинами параллелограмма.
А
Q
D
Р
F
В
E
С

11.

№ 568. Докажите, что четырехугольник – ромб, если его
вершинами являются середины сторон прямоугольника.
А
Q
Р
В
D
F
E
С

12.

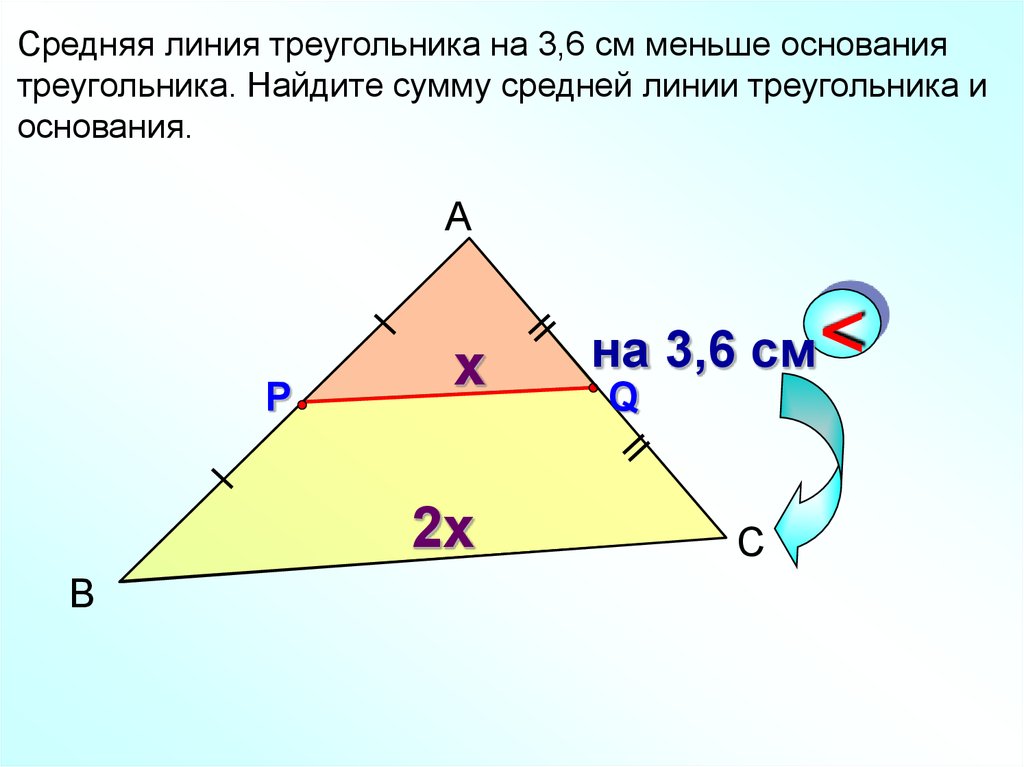
Средняя линия треугольника на 3,6 см меньше основания
треугольника. Найдите сумму средней линии треугольника и
основания.
А
Р
x
2x
В
на 3,6 см <
Q
С

13.

АВСD – параллелограмм, ОЕ и ОF – средние линии
треугольника АВС. Найти периметр параллелограмма.
В
F
510
Е
А
4
8
О
D
С

14.

Периметр параллелограмма АВСD равен 56 см, D=1200,
BD = AВ. Найдите периметр треугольника СМN, где М –
середина ВС, а N - середина СD. 14
В
М
7
С
7
7
14
14
N
А
600
14
D
14

15.

Периметр параллелограмма АВСD равен 60 см, а длина его
диагонали ВD равна 18 см. Точки К и Р – середины сторон АD
и АВ соответственно. Найдите периметр пятиугольника
ВСDКР.
В
С
18
Р
РАВСD=60см
9
рАВСD=30см
А
К
D
30
15
9
РВСDKP= ВС + СD + DK + BP + PK

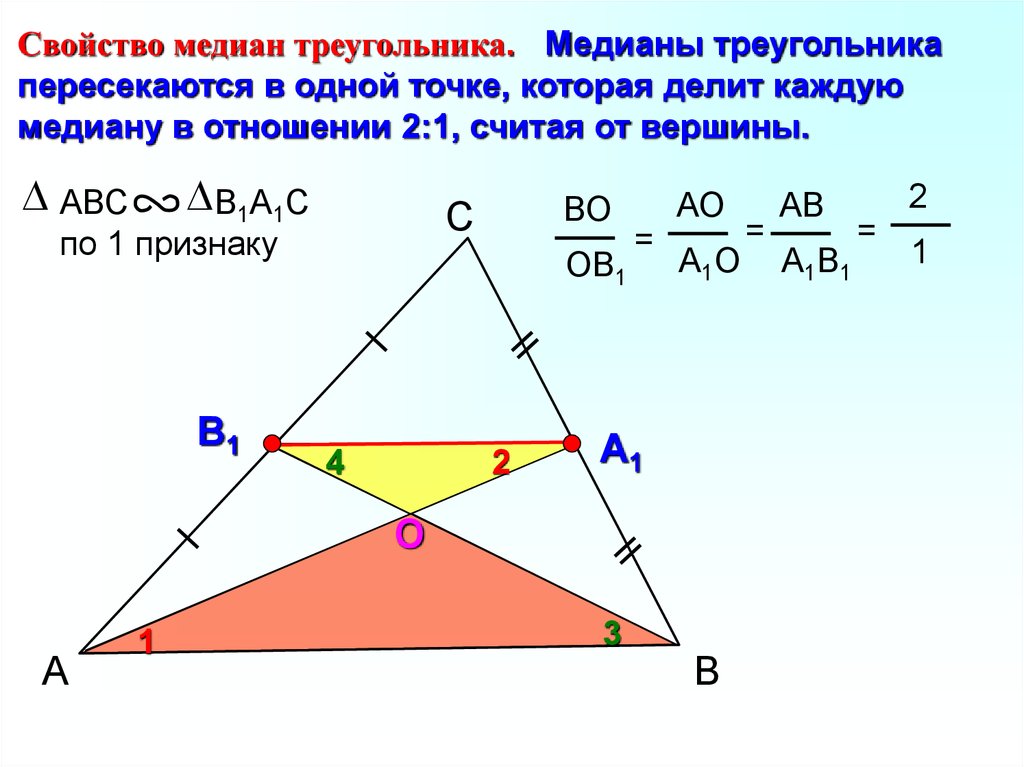
16.

Свойство медиан треугольника. Медианы треугольника
пересекаются в одной точке, которая делит каждую
медиану в отношении 2:1, считая от вершины.
AВС
В1А1С
С
по 1 признаку
В1
ВО
ОВ1
4
2
АО
=
А1О
А1
О
А
1
3
В
=
АВ
А1В1
2
=
1

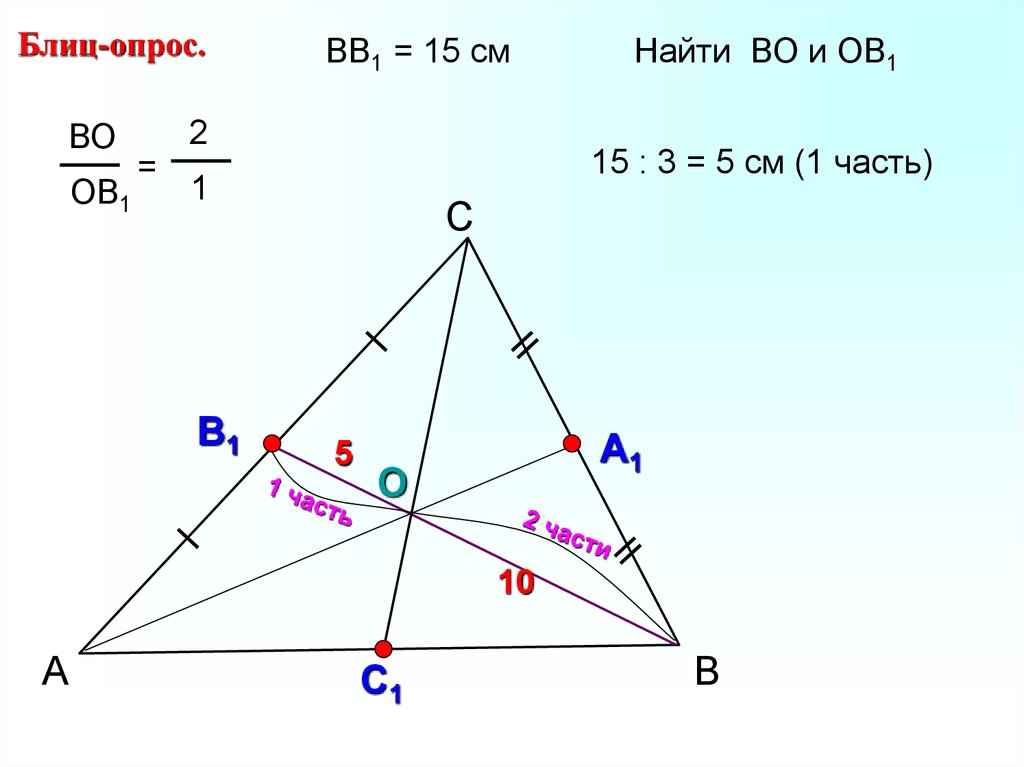
17.

Блиц-опрос.
ВО
ОВ1
ВВ1 = 15 см
2
=
15 : 3 = 5 см (1 часть)
1
В1
Найти ВО и ОВ1
С
5
А1
О
10
А
С1
В

18.

Блиц-опрос.
ВО
ОВ1
ОВ1 = 4 см
Найти ВО и ВВ1
2
=
ОВ1 = 4 см (1 часть)
1
В1
С
4
А1
О
8
А
С1
В

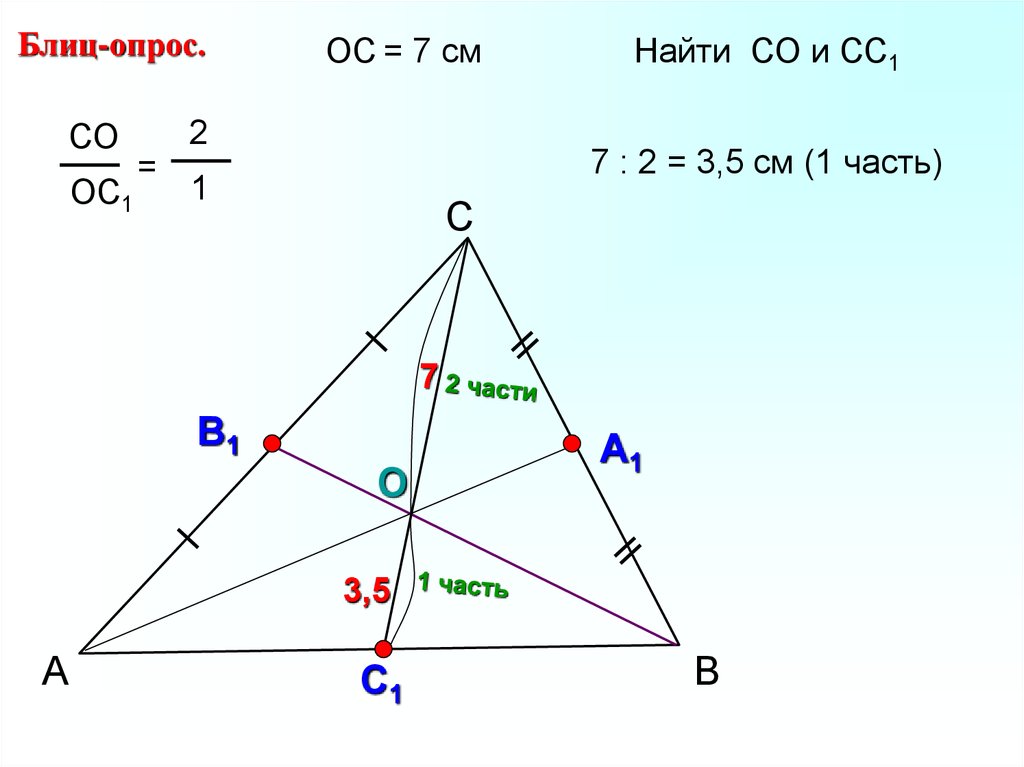
19.

Блиц-опрос.
СО
ОС1
ОС = 7 см
2
=
Найти СО и СС1
7 : 2 = 3,5 см (1 часть)
1
С
7
В1
О
А1
3,5
А
С1
В

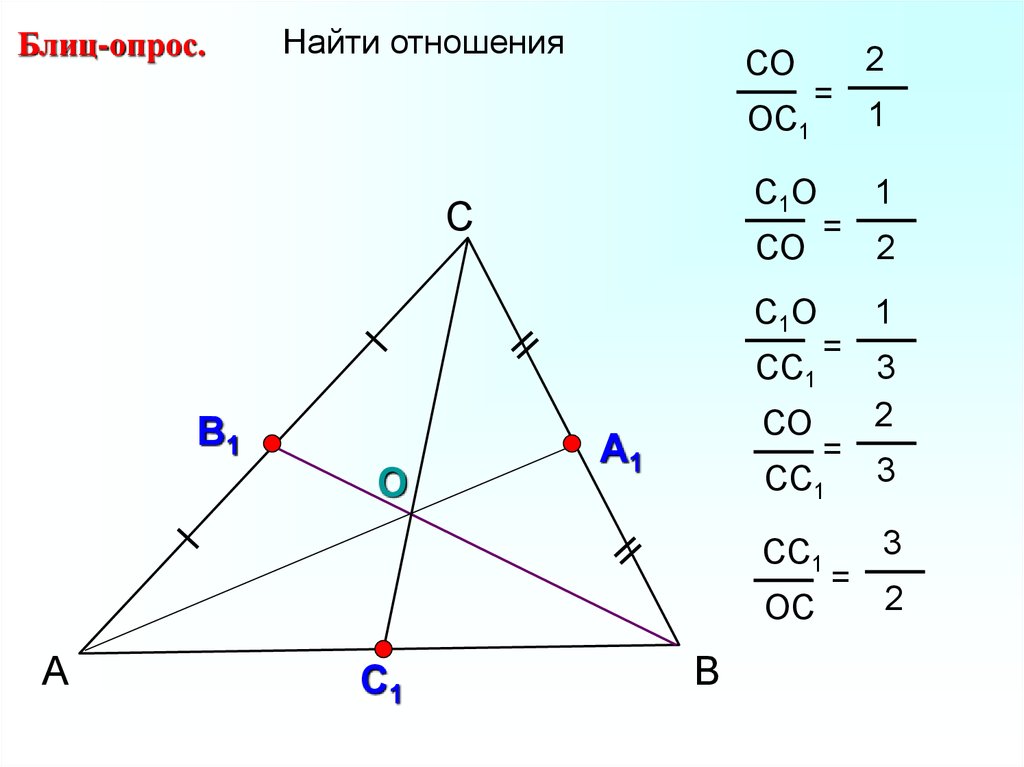
20.

Блиц-опрос.
Найти отношения
СО
ОС1
2
=
С1О
С
СО
С1О
СС1
В1
О
СО
А1
С1
В
1
=
2
1
=
=
3
2
СС1
3
СС1
3
ОС
А
1
=
2