Самовоздействие (самофокусировка) света

1.

САМОВОЗДЕЙСТВИЕ ( САМОФОКУСИРОВКА ) СВЕТА
The refractive index of many optical materials depends upon the intensity of
the light used to measure the refractive index nonlinear refractive index
Предсказано в 1962 г. Г.А. Аскарьяном.
«Воздействие луча на среду может быть настолько сильным, что создается перепад свойств
среды в луче и вне луча, что вызовет волноводное распространение луча и устранит
геометрическую и дифракционную расходимость. Это интересное явление можно назвать
самофокусировкой электромагнитного луча».
Самофокусировка - пороговый эффект: для ее наблюдения необходимо
превышение мощности излучения над критической мощностью самофокусировки
(от МВт в конденсированной среде до ГВт в газах).
n = n0 + n%
2 E
Нестационарная
(самофокусировка
импульсного излучения )
2
Оптический
эффект
Керра
Стационарная
(непрерывное излучение )
1

2.

САМОВОЗДЕЙСТВИЕ И САМОФОКУСИРОВКА СВЕТА
В нелинейных средах отлична от нуля кубичная нелинейность, (3) :
r (3)
r
r
r*
(3)
P (w ) = ˆ (w = w + w - w )ME (w ) E (w ) E (w )
Если ввести эффективную кубичную нелинейность среды (3)ef :
r (3)
r
2
(3) eff
Pi (w ) =
(w ) E (w ) Ei (w )
Pi (w )
то можно записать:
Di (w ) = Ei (w ) + 4p ( Pi L (w ) + Pi NL (w ))
2
= e 0 Ei (w ) + 4p (3) eff (w ) Ei (w ) Ei (w ) = n 2 (w ) Ei (w )
e ( E ) = e 0 + 4p
(3) eff
E
2
2

3.

В общем случае e и (3) - комплексные величины,
e '(w ) = e 0 '+ 4p Re (3) eff E (w )
обычная диэлектрическая
проницаемость
(соответствующая слабому
световому воздействию)
2
причем
e 0 '(w ) >> 4p Re (3) eff E (w )
2p (3) eff
n (w ) = e (w ) » n0 +
E
n0
или
n = n0 + n%
2 E
2
2
2
Временное
усреднение
Нелинейный показатель преломления – показывает,
с какой скоростью меняется показатель преломления с
ростом интенсивности света
E (w )
(3)
E (w )exp(ifNL )
3

4.

n = n0 + n%
2 E
2
,
n0 = 1 + 4pa
n2 – нелинейная добавка,
- линейный показатель преломления среды,
определяемая видом нелинейного взаимодействия.
2
4
n = n0 + n%
+ n4 E + ...
2 E
В общем виде:
Обычно нелинейный показатель преломления определяется кубичной нелинейностью;
высшие члены разложения могут играть роль, например, вблизи резонансов.
Альтернативный метод описания -
n = n0 + n2 I + n4 I 4 + ...
2
n%
= n2 I n2 =
2 E
é см 2 ù 16p 2 (3) eff
n2 ê
=
ú
2
Вт
n
ë
û
0 c
I=
8p
n%
2
cn0
cn0
2
E (w )
8p
- интенсивность света
4

5.

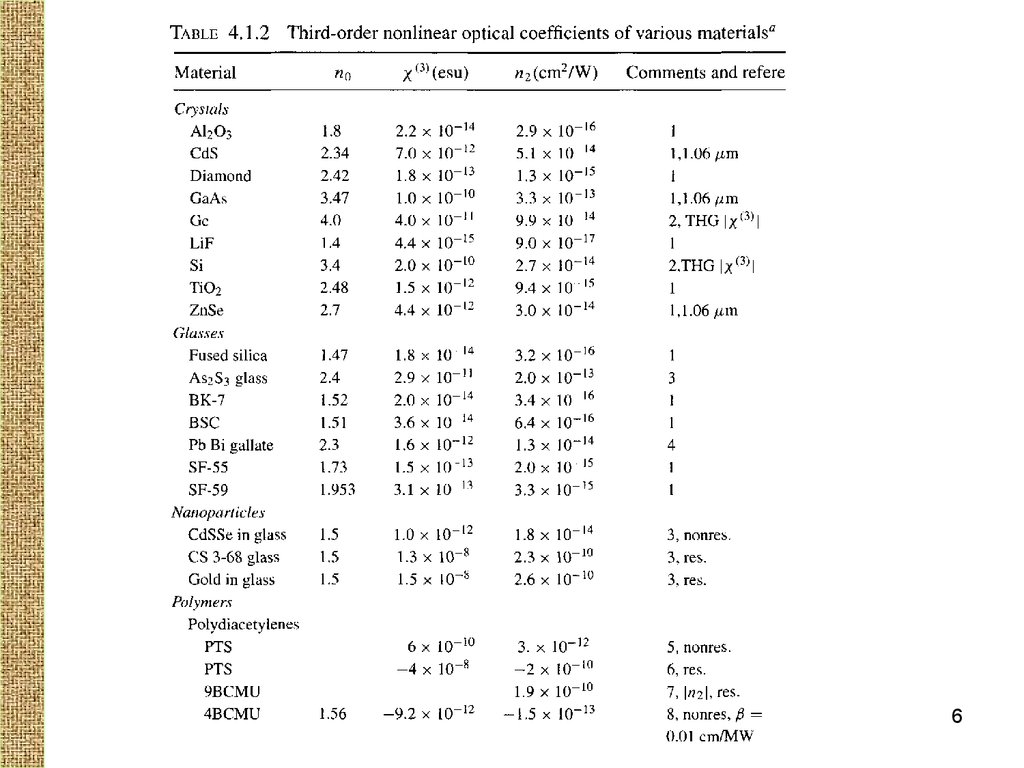
Типичные значения нелинейного показателя преломления
quartz :
nсм
Вт-16
2 = 3×10
2
/
I =1 MВт / см 2 n2 = 3×10-8
Хотя величина нелинейного показателя преломления очень мала, позже мы
покажем, что такое нелинейное взаимодействие в условиях фазового
синхронизма может приводить к сильнейшим эффектам!
5

6.

6

7.

НЕЛИНЕЙНАЯ РЕФРАКЦИЯ
Самодефокусировка
Дифракционая
расходимость
Самоканалирование
Самофокусировка
Изменение ширины волнового пучка при дифракции в линейной (1)
и нелинейных (2-4) средах
7

8.

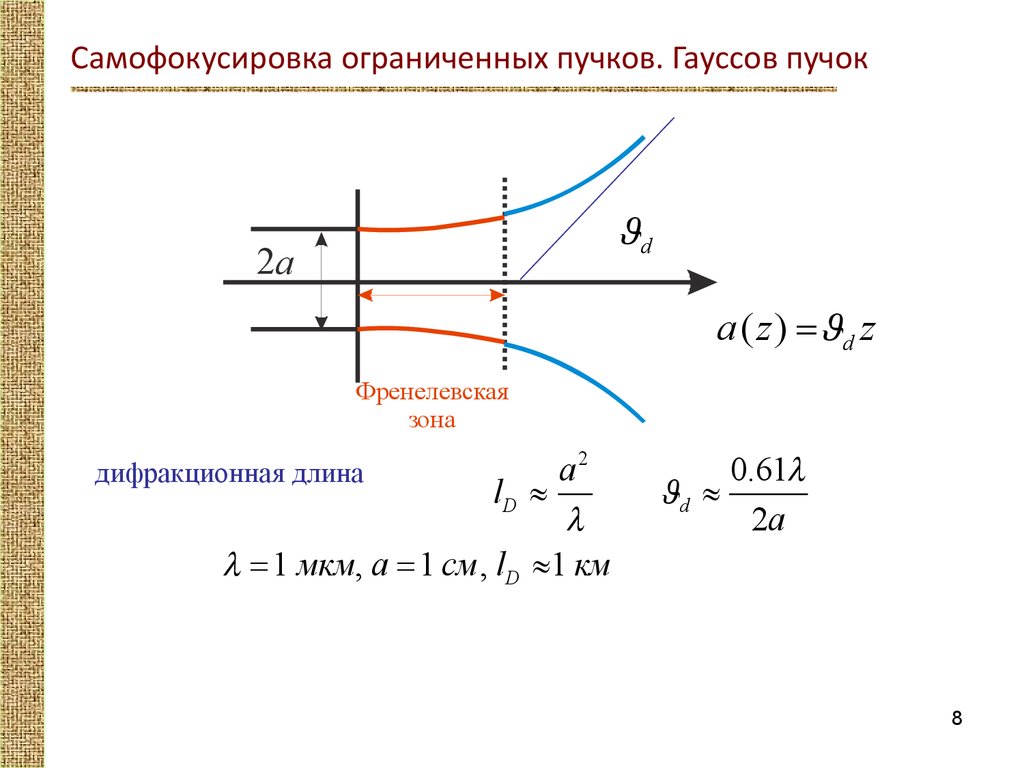
Самофокусировка ограниченных пучков. Гауссов пучок
Jd
2a
a ( z ) =Jd z
Френелевская
зона
a2
lD »
l
l = 1 мкм, a = 1 см , lD »1 км
дифракционная длина
0.61l
Jd »
2a
8

9.

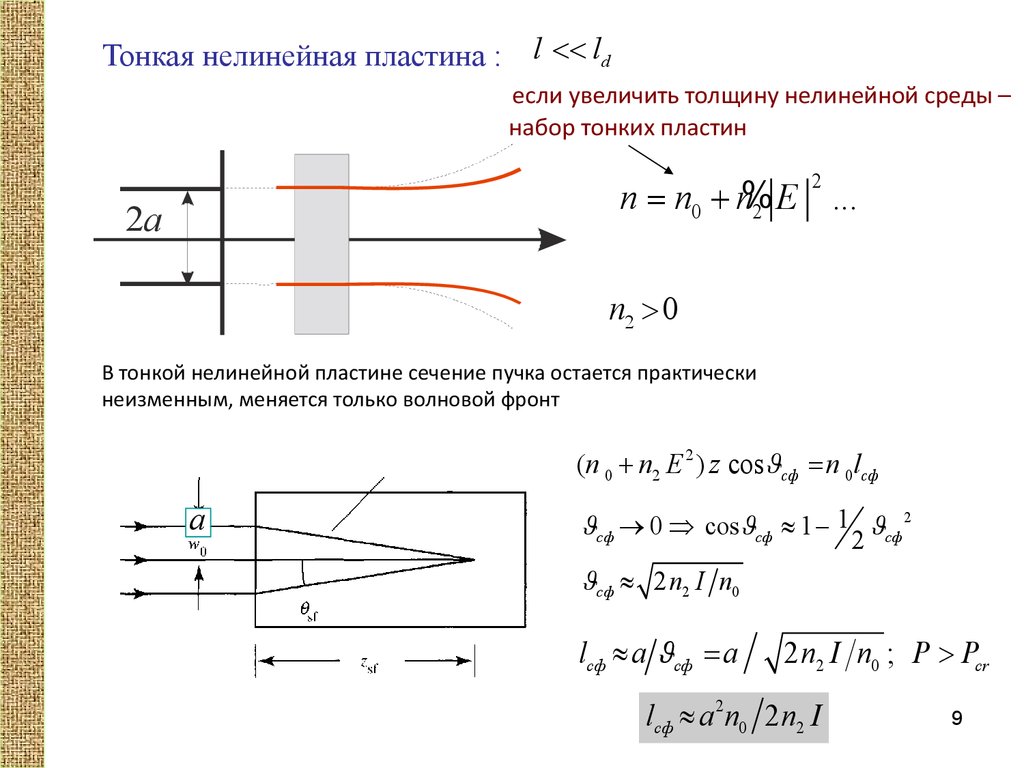
Тонкая нелинейная пластина : l << ld
если увеличить толщину нелинейной среды –
набор тонких пластин
2
n = n0 + n%
...
2 E
2a
n2 > 0
В тонкой нелинейной пластине сечение пучка остается практически
неизменным, меняется только волновой фронт
(n 0 + n2 E 2 ) z cosJсф = n 0lсф
a
Jсф ® 0 cos Jсф » 1 - 1 2 Jсф 2
Jсф » 2 n2 I n0
lсф » a Jсф = a
2 n2 I n0 ; P > Pcr
lсф » a 2 n0 2 n2 I
9

10.

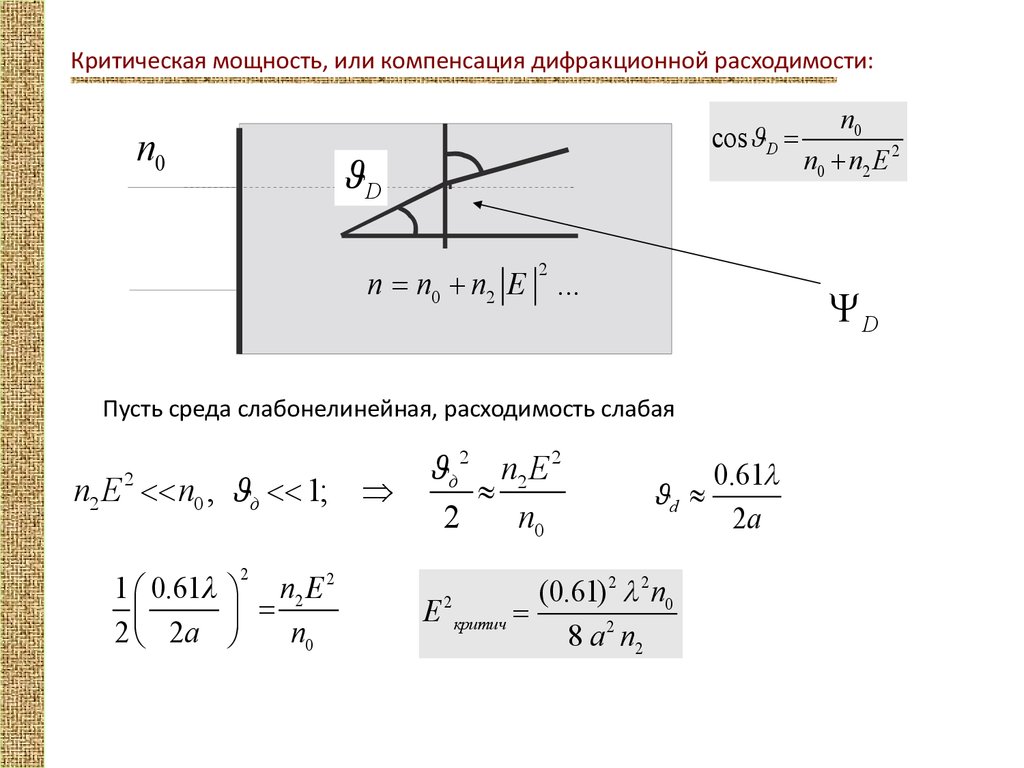
Критическая мощность, или компенсация дифракционной расходимости:
n0
cos JD =
JD
n0
n0 + n2 E 2
2
n = n0 + n2 E ...
YD
Пусть среда слабонелинейная, расходимость слабая
2
2
J
n
E
д
n2 E 2 << n0 , Jд << 1;
» 2
2
n0
2
1 æ 0.61l ö n2 E 2
ç
÷ =
2 è 2a ø
n0
Jd »
(0.61) 2 l 2 n0
E критич =
8 a 2 n2
2
0.61l
2a

11.

Что происходит в 
фокусе?
n = n 0 + n2 E 2 + n4 E 4 + .....
Длинные (нс) импульсы: основной нелинейный процесс - двухфотонное
поглощение
Короткие (фс) импульсы – нелинейности высших порядков ,
дефокусировка в самонаведенной лазерной плазме,
поглощение при многофотонной ионизации, ВКР, пробой
11

12.

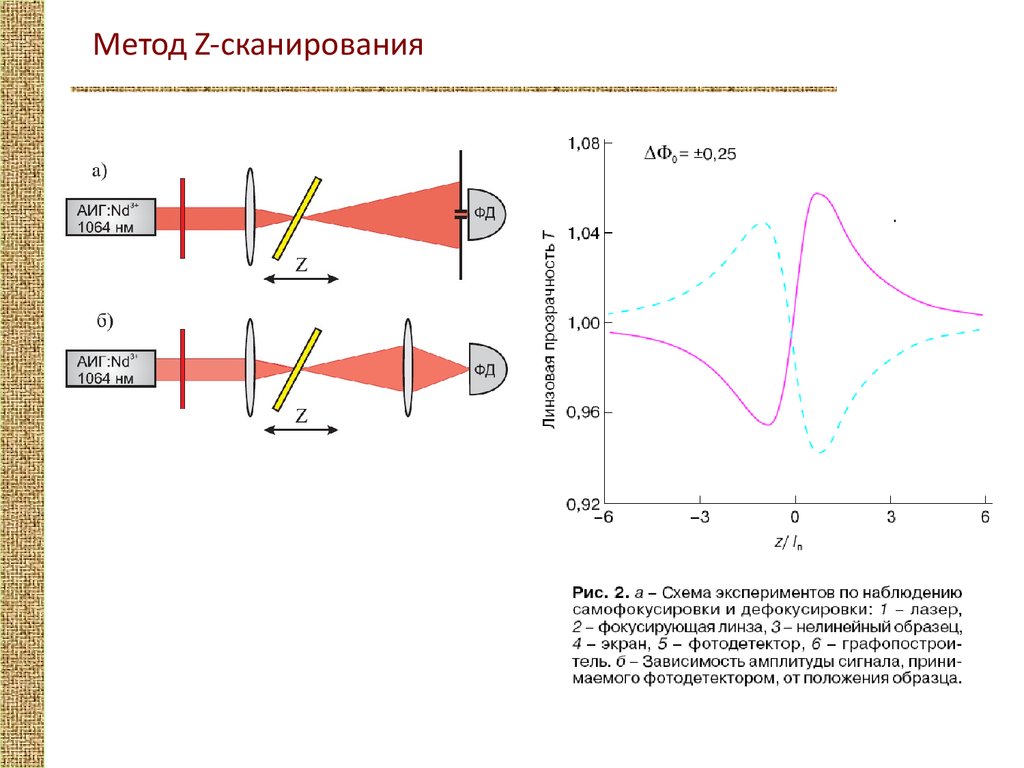
Метод Z-сканирования

13.

Эффекты, возникающие в средах с нелинейным показателем преломления
• Самофоксировка (само-дефокусировка) – различаются для
импульсного и непрерывного излучения
• Самоканалирование (self-trapping of light)
• Филаментация лазерных пучков
• Фазовая самомодуляция (phase conjugation)
• Оптическая бистабильность
13

14.

Следствия тензорной природы кубичной восприимчивости:
Эффект нелинейной рефракции определяется кубичной
восприимчивостью. Это тензор 4-го ранга (81 компонента)
тензорный характер эффекта
Для изотропной среды и случая :
21 компонента (четное число
индексов, соответствующих
каждой из осей x,y,z)
ijkl (w4 = w1 + w2 + w3 )
1111 = 2222 = 3333
1122 = 1133 = 2211 = 2233 = 3311 = 3322
1212 = 1313 = 2323 = 2121 = 3131 = 3232
1221 = 1331 = 2112 = 2332 = 3113 = 3223
1,2,3 = x, y, z
14

15.

4 отличные от нуля компоненты кубичной восприимчивости (для изотропной
нелинейной среды) связаны соотношением:
1111 = 1122 + 1212 + 1221
-это можно получить, если учесть инвариантность нелинейной поляризации при переходе между
двумя координационными системами, повернутыми на произвольный угол (450).
Т.о. кубичная восприимчивость может быть представлена в виде:
ijkl = 1122d ijd kl + 1212d ik d jl + 1221d ild jk
Рассмотрим, что дает этот результат для описания эффекта нелинейной рефракции,
ijkl (w = w + w - w )
1122 = 1212
ijkl (w = w + w - w ) = 1122 { d ijd kl + d ikd jl } + 1221 d ild jk
Эффект нелинейной
рефракции определяется
нелинейной поляризацией:
Или полностью в
векторной форме:
Pi (w ) = 3å ijkl (w = w + w - w )E j (w ) Ek (w ) El (-w )
Pi (w ) = 6 1122 Ei ( E × E* ) + 3 1221 Ei* ( E × E )
A º 3 1122 + 3 1212
1
P(w ) = A E ( E × E ) + B ( E × E ) E*
2
B/2
*
15

16.

1
P(w ) = A E ( E × E* ) + B ( E × E ) E*
2
Однофотонный резонанс
Двухфотонный резонанс
16

17.

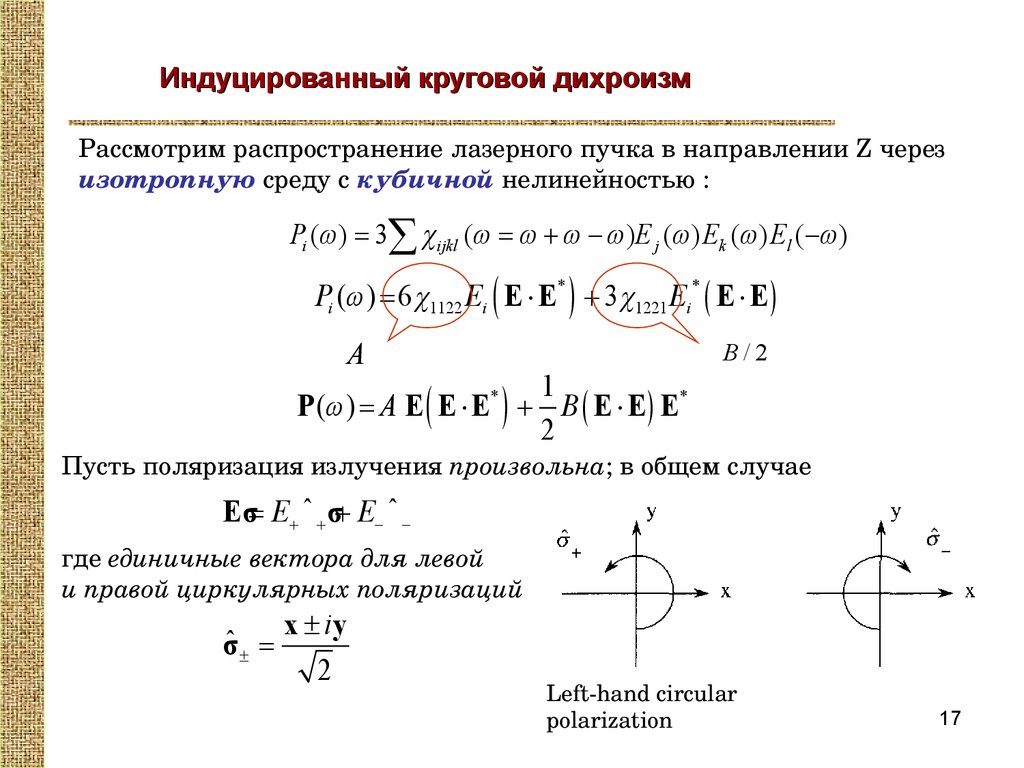
Индуцированный круговой дихроизм
Рассмотрим распространение лазерного пучка в направлении Z через 
изотропную среду с кубичной нелинейностью :
Pi (w ) = 3å ijkl (w = w + w - w )E j (w ) Ek (w ) El (-w )
Pi (w ) = 6 1122 Ei ( E × E* ) + 3 1221 Ei* ( E × E )
A
B/2
1
P(w ) = A E ( E × E ) + B ( E × E ) E*
2
*
Пусть поляризация излучения произвольна; в общем случае
Eσ= E+ ˆ + σ+ E- ˆ где единичные вектора для левой
и правой циркулярных поляризаций
σˆ ± =
x ± iy
2
Left­hand circular 
polarization
17

18.

1
2
Eσ= E+ ˆ + σ+ E- ˆ - P(w ) = A E ( E × E* ) + B ( E × E ) E*
Поскольку
σˆ *± = σˆ m , σˆ ± × σˆ ± = 0 , σˆ ± × σˆ m = 1
*
E × Eσ
= ( E+ ˆσ+ + E- ˆσ- ) ( E+* ˆσ*+ + E-* ˆ *- ) = E+* E+ + E-* E- = E+ + E2
2
E × Eσ= ( E+ ˆ σ+ + E- ˆ σ- ) ( E+ ˆ σ+ + E- ˆ - ) = E+ E- + E- E+ = 2 E+ E-
(
2
P(w ) = A E E+ + E-
2
) + B( E E ) E
*
+
-
Если теперь представить и нелинейную 
поляризацию через циркулярные составляющие
(
2
P+ = A E+ + E-
2
)
(
E+ + B ( E+ E- ) E-* = A E+ + E-
2
Аналогично
Pσ= P+ ˆ +σ+ P- ˆ 2
2
)
2
E+ + B E- E+ =
2
= A E+ E+ + ( A + B ) E- E+
2
2
P- = A E- E- + ( A + B) E+ E-
18

19.

Запишем эти равенства через нелинейные восприимчивости для циркулярно 
поляризованных волн, при этом введем нелинейные восприимчивости для 
левой и правой циркулярных поляризаций;
  эти выражения подставим в волновое уравнение
P± º E± ;
NL
±
NL
±
2
= A E± + ( A + B ) Em
2
(1) 2
2 NL
e
¶
E
(
z
,
t
)
4
p
¶
P
Ñ 2 E( z , t ) = 2
+
c
¶t 2
c 2 ¶t 2
В циркулярных поляризациях
e ± eff ¶ 2 E± ( z, t )
2
Ñ E± ( z , t ) = 2
c
¶t 2
e ± eff = e (1) + 4p ± NL
Решение этого уравнения дает значения для фазовых скоростей 
распространяющихся волн
eff
c / nгде
±, n
Учтем , 
что
±
= e±
{
2
n0 2 = e (1) n±2 = n0 2 + 4p ±NL = n0 2 + 4p A E± + ( A + B ) Em
{
2
}
}
æ 4p
2 ö
2
= n0 2 ç1 + 2 4p A E± + ( A + B ) Em ÷
è n0
ø
19

20.

2p
n0
{
2
2
}
Таким образом                                                                                      ,
n± » n0 +
A E± + ( A + B ) Em
т.е. левая и правая циркулярно поляризованные компоненты пучка 
распространяются с разными фазовыми скоростями
{
2p B
2
n º n+ - n- =
E- - E+
n0
2
}
(причем разность  n зависит только от коэффициента В).
Итак, эллипс поляризации будет вращаться по мере 
распространения в нелинейной среде. 
Найдем выражение для угла поворота.
Eσ
( z ) = E+σˆ + + E- ˆ - = Aσ+ ei n+w z /c ˆ + + Aσ- ei n-w z /c ˆ - =
= ( A+ ei (1/2) nw z / c σˆ + + A- e - i (1/2) nw z / c σˆ - ) ei (1/2)( n+ +n- )w z /c
Если ввести средний 
волновой вектор и угол, 
соответственно, как 
1
w
( n+ + n- ) ,üïï
2
c
ikm z
iq
- iq
ˆ
ˆ
Eσ
(
z
)
=
A
σ
e
+
A
e
e
(
)
ý
+ +
- 1w
ï
q =
z n
ïþ
2c
km º
20

21.

Eσ
( z ) = ( A+ ˆσ+ eiq + A- ˆ - e - iq ) eikm z
­ это уравнение для волны, имеющей ту же эллиптичность поляризации, 
что и падающая волна, но повернутую на угол  q :
Т.о. измерение угла поворота эллипса 
поляризации – метод  измерения 
нелинейного коэффициента В.
{
2p B
2
n º n+ - n- =
E- - E+
n0
2
}
Вращения эллипса поляризации нет, если 
1. Падающее излучение циркулярно поляризовано, т.е. существует 
s + или s -
2. Падающее излучение поляризовано линейно , 
E+ = E21

22.

Таким образом, достаточно интенсивный луч лазера может вызвать
заметное изменение показателя преломления среды =>
самофокусировка (дефокусировка) и нелинейное поглощение
Самофокусировка возникает при распространении в среде
ограниченных пучков
n2 > 0
- Как правило, в прозрачных средах – самофокусировка:
области максимальной интенсивности оказываются
оптически более плотными
n2 < 0
- Чаще всего, в средах с поглощением
Под действием света в веществе наводится керровская линза,
тип которой – собирающая или рассеявающая – зависит от знака
нелинейности
22

23.

«Сова стала объяснять, что такое Необходимая или Соответствующая Спинная
Мускулатура. Она уже объясняла это когда-то Пуху и Кристоферу Робину и с тех пор
ожидала удобного случая, чтобы повторить объяснения, потому что это такая штука,
которую вы спокойно можете объяснять два раза, не опасаясь, что кто-нибудь
поймет, о чем вы говорите.» А. Милн «Винни Пух и Все-Все-Все…»
(Квази)стационарная и нестационарная самофокусировка
Квазистационарная самофокусировка ( имп>> 0)
(длительность импульса много БОЛЬШЕ, чем время отклика среды).
- разбиение лазерного пучка на нити;
- след движущегося фокуса, оставляемого им на фотографии при большом
времени экспозиции
23

24.

Нестационарная самофокусировка
Если длительность импульса света МЕНЬШЕ или сравнима с временем
установления n ( имп 0) – необходимо учитывать изменение n за время
действия импульса нестационарная самофокусировка.
¶n
n(t ) » n0 + d T
¶t
-Искажение поперечного профиля пучка: задняя
часть импульса сжимается, попадая в среду с
наведенным передним фронтом импульса
показателем преломления – «горн».
24

25.

Тепловая самофокусировка
Поглощающая среда, I = I0exp(-a z).
dn
n(t ) » n0 + d T
dt
Лазерноиндуцированное
изменение Т
Вклад тепловых эффектов в нелинейность среды.
Нагрев среды при поглощении света изменение плотности изменение
показателя преломления (характерные времена до единиц сек).
Уравнение
теплопроводности:
¶T
cn 2
2
rc
= zÑ T + a
E0 exp ( -a z )
¶t
8p
теплоемкость
a I ( z)
единицы объема
c
c
z
r
a
- удельная теплоемкость
Лазерно индуцированное изменение
температуры вещества
- скорость света
dn
n T = n0 + d T
- теплопроводность (температуро-) ( )
dT
- плотность вещества
- коэффициент поглощения
В общем случае –
нелокальный эффект
самофокусировка
Механизмы: - изменение плотности вещества;
25
- спектральный сдвиг полосы поглощения
>0

26.

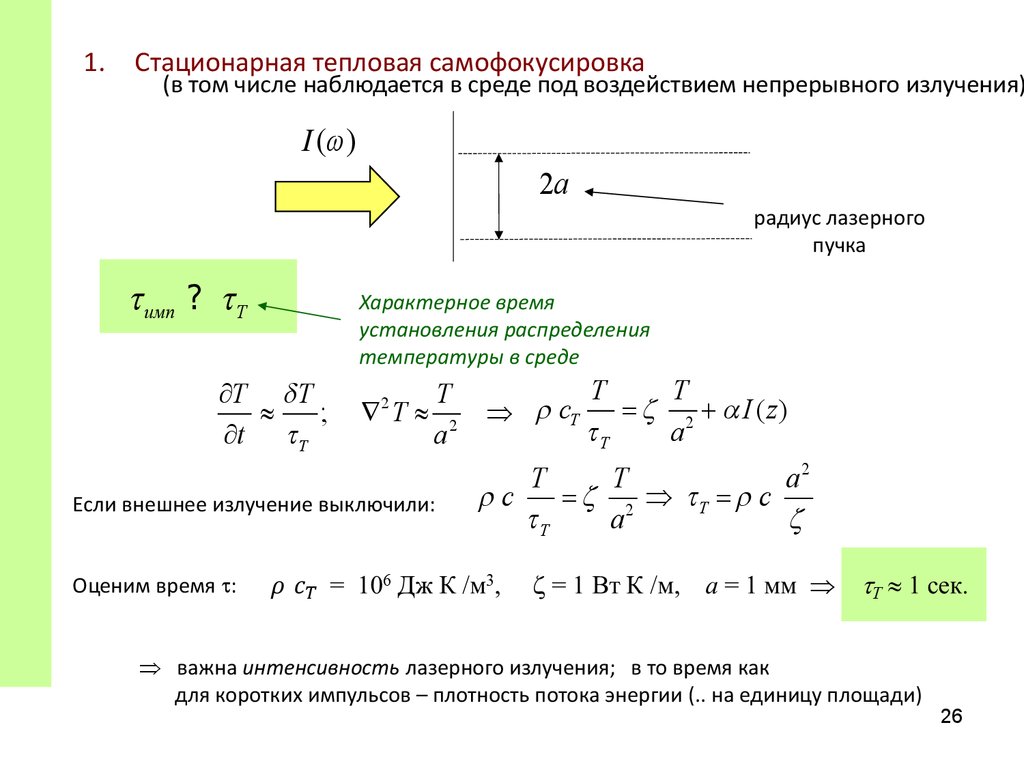
1.
Стационарная тепловая самофокусировка
(в том числе наблюдается в среде под воздействием непрерывного излучения)
I (w )
2a
радиус лазерного
пучка
имп ? T
¶T d T
»
;
¶t T
Характерное время
установления распределения
температуры в среде
T
Ñ T» 2
a
2
Если внешнее излучение выключили:
r cT
T
T
= z 2 + a I ( z)
T
a
T
T
a2
rc
= z 2 T = r c
T
a
z
Оценим время :
важна интенсивность лазерного излучения; в то время как
для коротких импульсов – плотность потока энергии (.. на единицу площади)
26

27.

Тепловой механизм изменения показателя преломления
среды под действием непрерывного излучения
Для оценки максимальной температуры
I (w )
2a
¶T
cn 2
2
rc
= zÑ T + a
E0 exp ( -a z )
¶t
8p
¶T
T
» 0 ; Ñ2 T » 2
Температура в
¶t
a
центре лазерного
a a 2 I max
T
пучка
- a I = z 2 Tmax »
a
z
2
2
dn
a
×
a
æ dn ö a I max a
æ
ö
n = ç ÷
, n = nT(2) I max , nT(2) = ç ÷
z
è dT ø
è dT ø z
= 10-5 К-1 ,
a = 1 см-1 ,
a = 1 см
» 3 10-5 см2 / Вт
nсм
Вт-16
2 = 3 10
2
/
Т.о. термические эффекты являются доминирующими в изменении нелинейного
показателя преломления среды под действием непрерывного лазерного излучения
27

28.

имп T
2. Нестационарная самофокусировка
-
необходимо вначале учитывать процесс установления температуры в нелинейной среде
Невозможность описания отклика среды в терминах
, поскольку он определяется
изменяющимся за время импульса (нелинейным) показателем преломления
rc
¶T
cn 2
= zÑ 2T + a
E0 exp ( -a z ) ;
¶t
8p
Нелинейный показатель
преломления
c n E02 t
d T (t ) = a
8p r c
В каком случае
термическая
нелинейность будет
равна электронной?
n ( T ) = n0 +
n2 (t ) =
Время установления Т
¶T d Tmax
»
¶t имп
- т.к. за время имп ничтожно
малая часть энергии уходит
из области взаимодействия
I max
d Tmax = a
имп
r0z
dn
dT
dT
dn c n
t
dt 8pr c
I
dn
dn
d Tmax =a max имп
= nel (2) I max
dT
r0z
dT
имп
nel (2) r0z
³
» 30 пс
d n dT a
при nel (2) » 10-16 см
2
Вт
28