Similar presentations:
Модуляция света
1. МОДУЛЯЦИЯ СВЕТА
2. Модуляция света
Модуляция света – это изменение его параметров взависимости от управляющего (модулирующего)
сигнала. С ее помощью производят наложение
информации на световую волну или световой поток,
осуществляющие ее перенос.
Из характеристики световой волны видно, что,
модулировать, т.е. целенаправленно изменять, можно:
амплитуду
(интенсивность),
частоту,
фазу,
поляризацию,
направление
распространения
и
пространственное распределение волны или светового
потока. В оптической электронике наибольшее
распространение как наиболее эффективные получили
амплитудная и фазовая модуляция.
3.
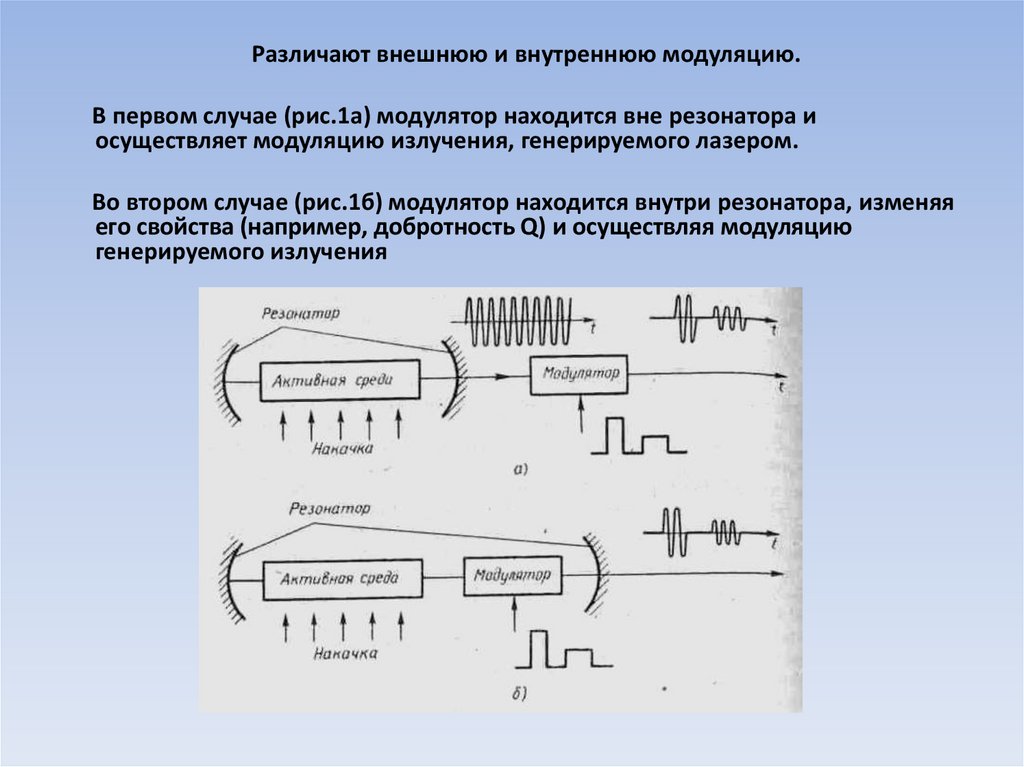
Различают внешнюю и внутреннюю модуляцию.В первом случае (рис.1а) модулятор находится вне резонатора и
осуществляет модуляцию излучения, генерируемого лазером.
Во втором случае (рис.1б) модулятор находится внутри резонатора, изменяя
его свойства (например, добротность Q) и осуществляя модуляцию
генерируемого излучения
4.
Важнейшими характеристиками оптических модуляторов являются:а) глубина модуляции:
h = (Imax-Imin)/I max
где Imax и Imin – интенсивности света при полностью открытом и
закрытом состоянии модулятора;
б) ширина полосы пропускания или диапазон модулирующих частот Δν,
которые определяются как разность между верхней и нижней частотами, при
которых глубина модуляции уменьшается на 50% от максимального значения;
полоса частот Δν определяет предельный объем информации, который
можно передать с помощью данного модулятора;
5.
в) рабочая апертура – тот угол, измеряемый в градусах или стерадианах, впределах которого оптическое излучение может быть введено в модулятор;
г) спектральная область – область длин волн, в которой модулятор способен
работать;
д) рабочее напряжение или напряжение полуволнового смещения – те
величины сигнала, которые необходимо подать на вход модулятора, чтобы
перевести его из «открытого» состояния в «закрытое»;
е) потери, вносимые модулятором, выражаемые, как правило, в
децибелах:
b = 10 lg (Io/Imax)
где I0 – интенсивность света в отсутствие модулятора, Imax – интенсивность
света, прошедшего через модулятор в открытом состоянии;
6.
ж) потребляемая мощность на единицу ширины полосы пропусканиямодулятора Р/ Δf, выражаемая обычно в Вт/ГГц.
Для осуществления модуляции необходимо, чтобы управляющий сигнал
воздействовал на свет. Т.е. работа оптического модулятора должна основываться
на процессах взаимодействия света с веществом. Возможно использование
эффектов, рассмотренных выше: электрооптические, магнитооптические и
пьезооптические эффекты.
7.
Соответствующие модуляторы называются электрооптическими,магнитооптическими и пьезооптическими или акустооптическими, если
деформация в кристалле создается с помощью акустической волны.
По соотношению характерных геометрических размеров рабочей области
модулятора к длине световой волны и вытекающим отсюда отличиям в
системах
ввода излучения различают объемные и волноводные модуляторы.
Первые работают с плоскими волнами.
Вторые являются составными элементами оптических интегральных схем и
волоконной оптики.
Наибольшее значение как отдельные элементы оптической электроники
получили электрооптические и акустооптические модуляторы.
8.
Магнитооптический эффект Фарадея – изменение параметров показателяпреломления некоторых материалов под действием магнитного поля,
создаваемого источником модулирующего сигнала.
Упругооптический эффект –изменение параметров показателя преломления
некоторых материалов под действием акустической (или механической) волны,
создаваемой источником модулирующего сигнала (эффект Брэгга, эффект Рамана
– Ната).
Электроабсорбционный эффект – изменение параметров прозрачности
некоторых материалов под действием электрического поля, создаваемого
источником модулирующего сигнала.
9. МОЛЕКУЛЯРНЫЕ МАТЕРИАЛЫ ДЛЯ ОПТОЭЛЕКТРОНИКИ
Для современной оптоэлектроники кроме существующих сейчас мощныхисточников света необходимы материалы, обрабатывающие световую
информацию. Для модуляции фазы или амплитуды света необходимо
модулировать коэффициент преломления материала. Для этого используются
материалы с нелинейными оптическими свойствами. Причины больших
нелинейных оптических восприимчивостей в органических материалах лежит в
большой поляризуемости облака -электронов в сопряженных системах.
Большое смещение заряда при малых приложенных полях приводит к
нелинейному отклику, а следовательно, и к модуляции коэффициента
преломления. Кроме того, индуцированная таким образом поляризация, будучи
чисто электронной по природе, имеет время ответа порядка или меньше одной
фемптосекунды.
Кроме нелинейно оптических, существуют органические фоторефрактивные
материалы, которые используются для записи оптического изображения в
голографии. Органические материалы, обладающие фотохромными свойствами,
могут быть использованы для записи информации или как оптические триггеры.
10.
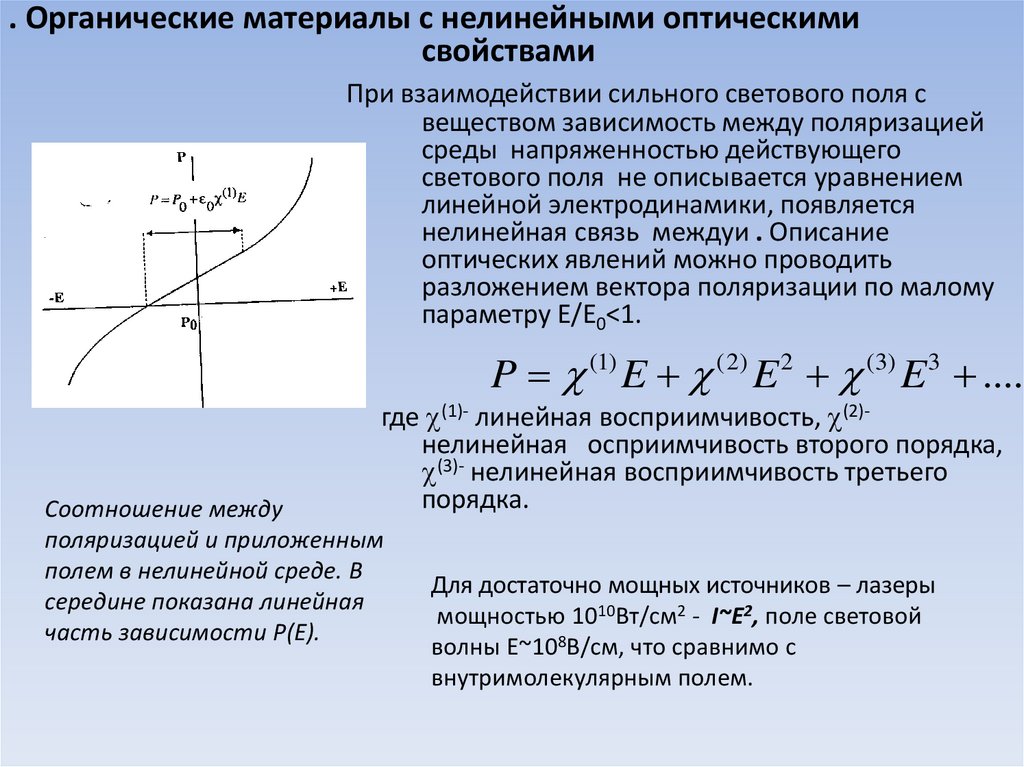
. Органические материалы с нелинейными оптическимисвойствами
При взаимодействии сильного светового поля с
веществом зависимость между поляризацией
среды напряженностью действующего
светового поля не описывается уравнением
линейной электродинамики, появляется
нелинейная связь междуи . Описание
оптических явлений можно проводить
разложением вектора поляризации по малому
параметру E/E0<1.
P = E E E ....
(1)
(2)
2
(3)
3
где (1)- линейная восприимчивость, (2)нелинейная осприимчивость второго порядка,
(3)- нелинейная восприимчивость третьего
порядка.
Соотношение между
поляризацией и приложенным
полем в нелинейной среде. В
середине показана линейная
часть зависимости Р(Е).
Для достаточно мощных источников – лазеры
мощностью 1010Вт/см2 - I~E2, поле световой
волны E~108В/см, что сравнимо с
внутримолекулярным полем.
11.
Pассмотрим меняющееся во времени поле световой волны E(t)=E0cos( t).Компонента поляризации материала возникающая во втором члене выражения
может быть выражена следующим образом
P(2)=1/2 0( (2)E02+ (2) E02cos(2 t))
Видно, что поляризация имеет одну постоянную компоненту и одну на частоте
2 . Это результируется в удвоении частоты падающего света после прохождения
через материал (генерация второй гармоники) и в появлении постоянного
электрического поля (эффект выпрямления света).
Для применений наиболее важным оказывается возникающий в этом случае
линейный электрооптический эффект (эффект Поккельса). Если образец
облучается лазером и к нему приложено постоянное или слабо меняющееся
электрическое поле Е(0), результирующая поляризация может быть записана в
виде:
P(2)=2 0 (2) E0cos( t)E(0)
Видно, что появляется линейная зависимость между поляризацией и постоянным
электрическим полем. Для описания этого эффекта часто пользуются
электрооптическим коэффициентом – r, который может быть выражен через
(2)следующим образом: (2)=n4r/2. Поскольку (2)является тензором 3 ранга, он
не равен нулю только в нецентросимметричных средах.
12.
Эффекты третьего порядка - более слабые по сравнению с эффектами второгопорядка, они получаются при разложении 3-го члена в выр.
P(3)=3/4 (3)E02 E0cos( t)+ (3) E02/4E0 cos(3 t))
Эти эффекты связаны с утроением частоты (генерация третьей гармоники) и с
изменением коэффициента преломления, который можно записать следующим
образом: n=n0+ nI, где I–интенсивность света, n= (3)/n02c 0 -изменение
коэффициента преломления. Это означает, что с помощью данного эффекта
можно управлять светом с помощью света, т.е. использовать такие среды для
полностью оптического компьютера.
Следующий вопрос – о микроскопической природе нелинейности или как
построить среду с оптической нелинейностью на молекулярном уровне. Каждая
молекула может рассматриваться как отдельный источник нелинейной
поляризации, и, если расстояние между молекулами значительно меньше длины
волны падающего света, то обьемный нелинейный коэффициент может
рассматриваться как сумма молекулярных коэффициентов с некоторой
коррекцией (F), учитывающей взаимную ориентацию молекул. Так, обьемные
значения нелинейных коэффициентов (2) и (3) могут быть выражены через
соответствующие молекулярные коэффициенты b и .
(2)=NbF
(3)=N F
13.
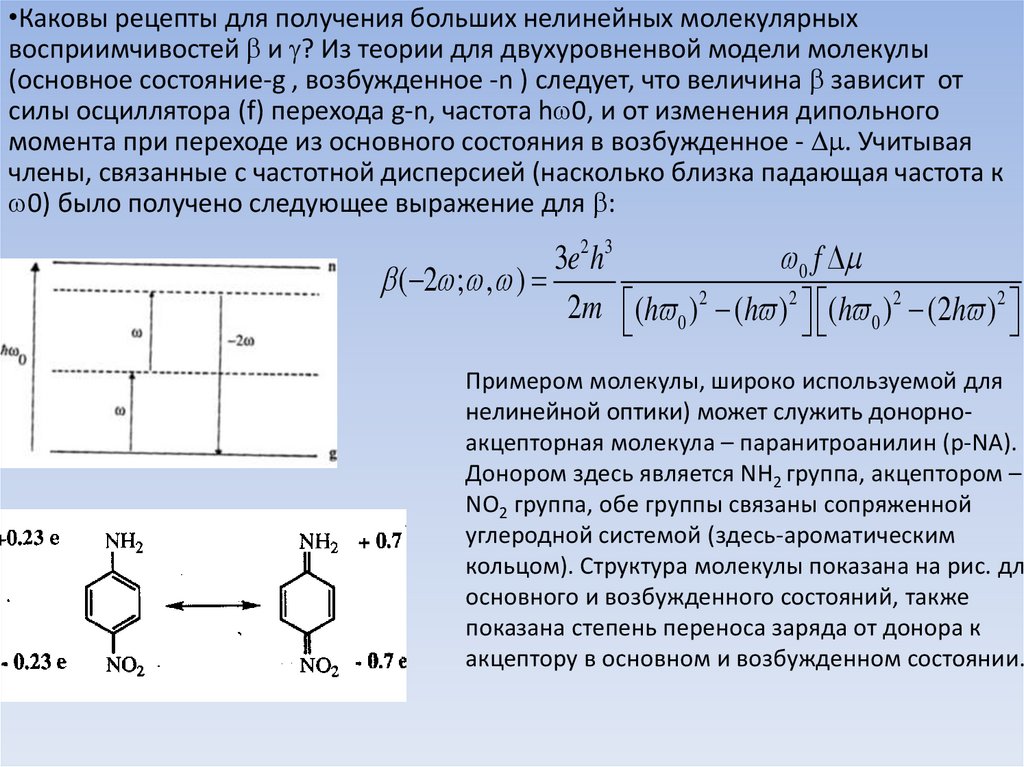
•Каковы рецепты для получения больших нелинейных молекулярныхвосприимчивостей b и ? Из теории для двухуровненвой модели молекулы
(основное состояние-g , возбужденное -n ) следует, что величина b зависит от
силы осциллятора (f) перехода g-n, частота h 0, и от изменения дипольного
момента при переходе из основного состояния в возбужденное - . Учитывая
члены, связанные с частотной дисперсией (насколько близка падающая частота к
0) было получено следующее выражение для b:
0 f
3e2 h3
b ( 2 ; , ) =
2m (h 0 )2 (h )2 (h 0 )2 (2h )2
Примером молекулы, широко используемой для
нелинейной оптики) может служить донорноакцепторная молекула – паранитроанилин (p-NA).
Донором здесь является NH2 группа, акцептором –
NO2 группа, обе группы связаны сопряженной
углеродной системой (здесь-ароматическим
кольцом). Структура молекулы показана на рис. для
основного и возбужденного состояний, также
показана степень переноса заряда от донора к
акцептору в основном и возбужденном состоянии.
14.
Дизайн молекул с большими значениямb заключается в подборе наиболее
сильных донорных -NH2, N(CH3)2 и
акцепторных- CN, NO2 групп, и в
увеличении длины сопряженной связи
между молекулами. Последний эффект
проиллюстрирован в таблице, n-число
сопряженных звеньев.
•Как перейти от таких дипольных молекул к обьемному материалу с большой
нелинейной поляризуемостью (2)? Проблема состоит в том, что при
кристаллизации в большинстве случаев дипольные молекулы выстраиваются
так, чтобы их дипольные моменты были направлены противоположно. В этом
случае результирующая оптическая поляризуемость близка к нулю. Существует,
однако, несколько способов решения данной проблемы. Один из них –
нанесение тонких упорядоченных молекулярных слоев методом ЛэнгмюраБлоджетт), при этом мономолекулярные слои наносятся последоваательно, так,
чтобы дипольные моменты молекул были направлены в одну сторону.
Исключение-кристаллы мочевины (молекулы мочевины обладают
квадрупольным моментом) которые обнаруживают большое значение (2).
C
NH2
NH2
15.
•Другой способ состоит в получении так называемыхполяризованных полимеров.
•Полярные донороно-акцепторные молекулы внедряются в
полимерную матрицу (их содержание может достигать 20-30
весовых процентов). Чтобы получить необходимую
нецентросимметричную среду, полимер нагревается до
температуры стеклования и прикладывается электрическое поле
для параллельного выстраивания диполей. После быстрого
охлаждения диполи остаются в замороженном состоянии. Если
поляризующее электрическое поле Ez прикладывалось в
направлении Z, то усредненную обьемную нелинейную
восприимчивость можно записать следующим образом:
( 2)
zzz
NFb zzz z Ez
5kT
–где — дипольный момент молекул, Т — температура
стеклования.
•Материалы с большой нелинейностью (2) используются в
электро-оптических волноводах и для генерации второй
гармоники.
•,
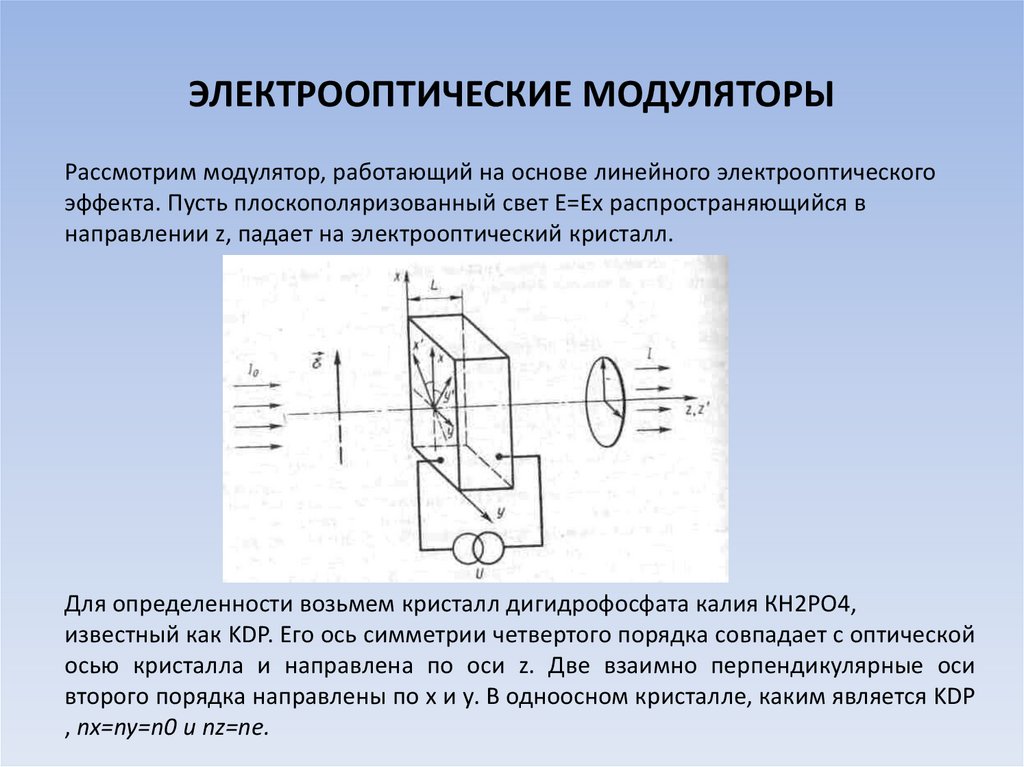
16. ЭЛЕКТРООПТИЧЕСКИЕ МОДУЛЯТОРЫ
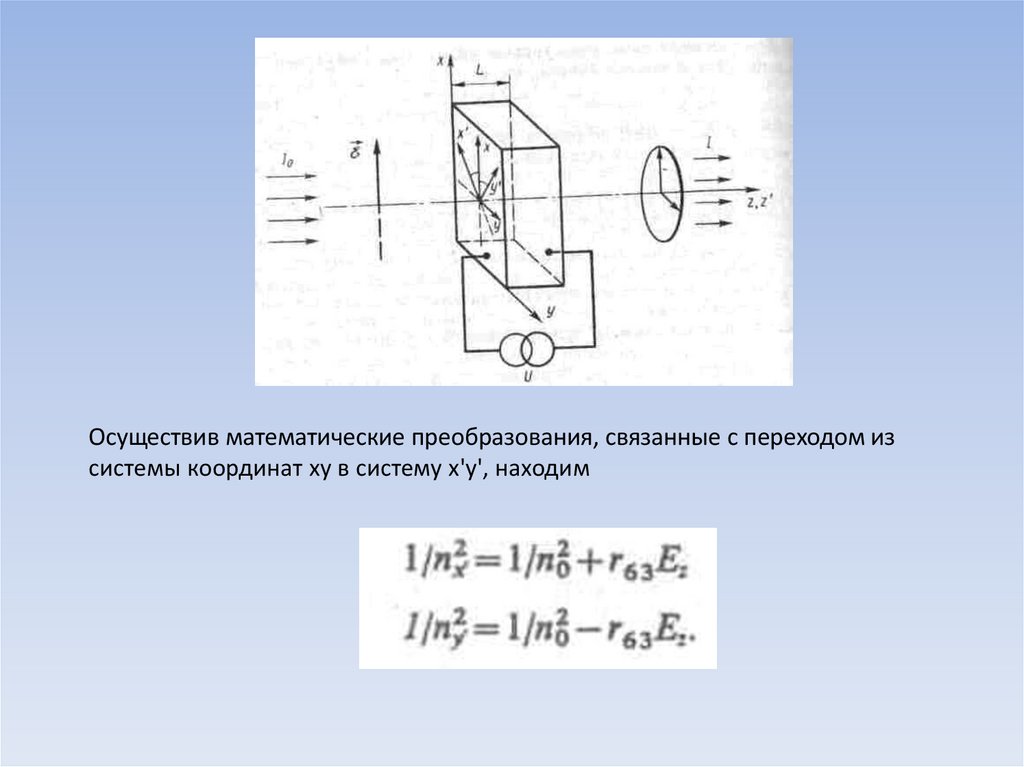
Рассмотрим модулятор, работающий на основе линейного электрооптическогоэффекта. Пусть плоскополяризованный свет Е=Ех распространяющийся в
направлении z, падает на электрооптический кристалл.
Для определенности возьмем кристалл дигидрофосфата калия КН2РО4,
известный как KDP. Его ось симметрии четвертого порядка совпадает с оптической
осью кристалла и направлена по оси z. Две взаимно перпендикулярные оси
второго порядка направлены по х и у. В одноосном кристалле, каким является KDP
, nx=ny=n0 и nz=ne.
17.
При приложении поля Ez вдоль направления z уравнение эллипсоидапоказателя преломления примет вид:
(3)
Чтобы это уравнение привести к диагональному виду, необходимо выбрать
систему координат x'y'z' с осью z, совпадающей с z и осями х' и у',
повернутыми на 45° относительно х и у. В этой системе координат уравнение
(3) преобразуется к диагональному виду:
(4)
18.
Осуществив математические преобразования, связанные с переходом изсистемы координат ху в систему х'y', находим
19.
Учитывая, что r63Ez <<1/ n0 , получаем:Аналогичные соотношения можно получить для коэф. диэлектрической
непроницаемости:
откуда находим изменение показателя преломления, вызванное электрическим
полем:
20.
Таким образом, если на электрооптический кристалл падает световая волна,поляризованная в плоскости xz, то, раскладывая ее на две компоненты Ех и Еу,
получаем для них изменение показателя преломления:
и вызванные этим изменением фазовые сдвиги для Еу` и Еx` – компонент
световой волны:
так что общий фазовый сдвиг:
пропорционален приложенному напряжению U. Если на вход такого модулятора
падает плоская монохроматическая волна
21.
то по прохождении электрооптического кристалла x` и y`-компоненты этойволны:
имеют фазовый сдвиг, непосредственно зависящий от приложенного
напряжения, так что по схеме рис.2 можно осуществлять фазовую модуляцию
световой волны.
22.
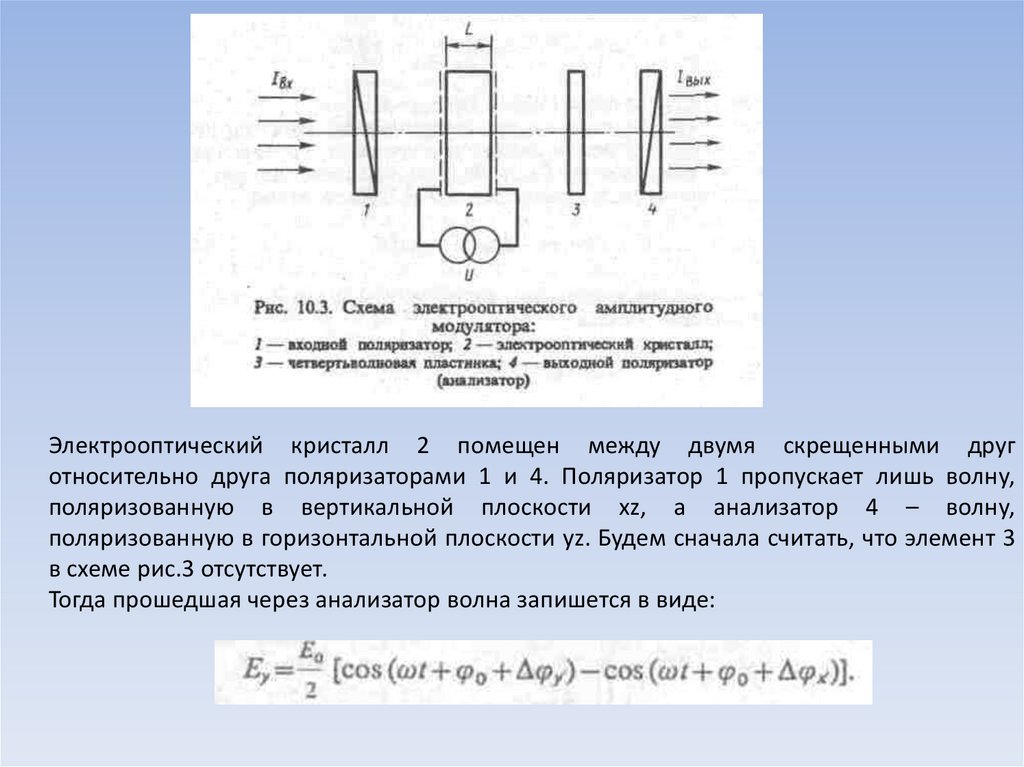
Электрооптический кристалл 2 помещен между двумя скрещенными друготносительно друга поляризаторами 1 и 4. Поляризатор 1 пропускает лишь волну,
поляризованную в вертикальной плоскости xz, а анализатор 4 – волну,
поляризованную в горизонтальной плоскости yz. Будем сначала считать, что элемент 3
в схеме рис.3 отсутствует.
Тогда прошедшая через анализатор волна запишется в виде:
23.
Приимеем
Интенсивность прошедшего излучения, которое определяется усреднением
Еy за период
будет
Зависимость оптического пропускания модулятора от приложенного
напряжения
где I0 – интенсивность света, падающего на кристалл (отражением и
поглощением в кристалле и оптических элементах схемы пренебрегаем).
24.
Зависимость оптического пропускания модулятора от приложенногонапряжения
которое можно переписать в виде
называется напряжением полуволнового смещения. При U= U λ/2 сдвиг фаз
соответствует λ/2, плоскость поляризации падающей волны после прохождения
электрооптического кристалла поворачивается на 90° и пропускание модулятора
максимально.
25.
Модулятор с продольном полем применяется для широких световых пучков.Очевидны два недостатка такого модулятор.
Во-первых, электроды, с помощью которых прикладывается электрическое
напряжение к кристаллу, должны пропускать свет, т.е. быть полупрозрачными,
что вызывает нежелательные потери.
Во-вторых, для работы такого модулятора требуются большие напряжения,
порядка 15 кВ.
26. АКУСТООПТИЧЕСКИЕ МОДУЛЯТОРЫ
Их принцип действия основан на акустооптическом эффекте, связанном сизменением показателя преломления оптической среды под влиянием
механических напряжений, сопровождающих прохождение акустической волны
через эту среду.
Акустическая волна длиной Λ вызывает пространственное изменение показателя
преломления, обусловленное пьезооптическими эффектами. Обычно
используется линейный упругооптический (фотоупругий) эффект.
Линейный упругооптический (фотоупругий) эффект заключается в том, что
показатель преломления среды изменяется пропорционально механической
деформации. Если к кристаллу приложить механическое напряжение то в нем
появятся деформации, что в свою очередь приведет к изменению
характеристик эллипсоида показателя преломления. При линейном эффекте
изменение коэффициентов оптической индикатрисы может быть записано в
виде
27.
28.
29.
С помощью акустической волны, генерируемой, например, каким-либопьезоэлектрическим устройством, в оптическом элементе модулятора создается
заданный профиль показателя преломления. Проще всего осуществить
периодическое изменение Δn, создавая для света своеобразную дифракционную
решетку.
Проходя через эту решетку или отражаясь от нее, световая волна будет испытывать
дифракцию и отклоняться. Это отклонение с помощью системы линз и диафрагм
может быть преобразовано в амплитудную модуляцию. Изменяя шаг решетки и ее
глубину путем изменения частоты и амплитуды акустической волны, возможно
осуществлять модуляцию света.
30.
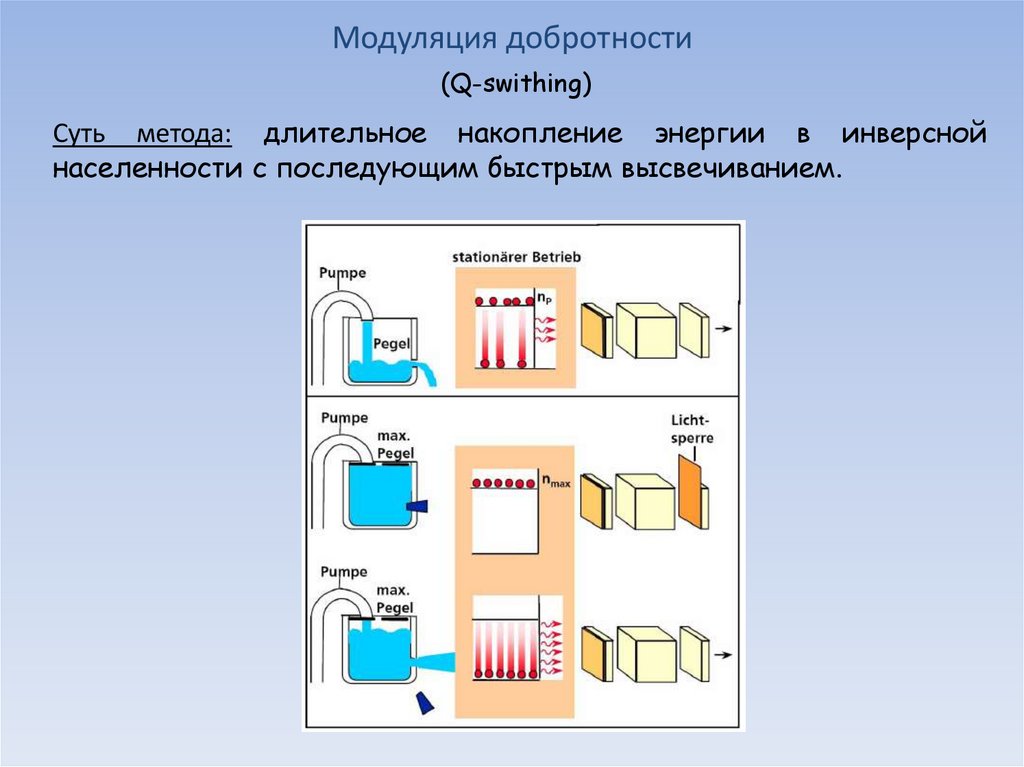
Модуляция добротности(Q-swithing)
Суть метода: длительное накопление энергии в инверсной
населенности с последующим быстрым высвечиванием.
31.
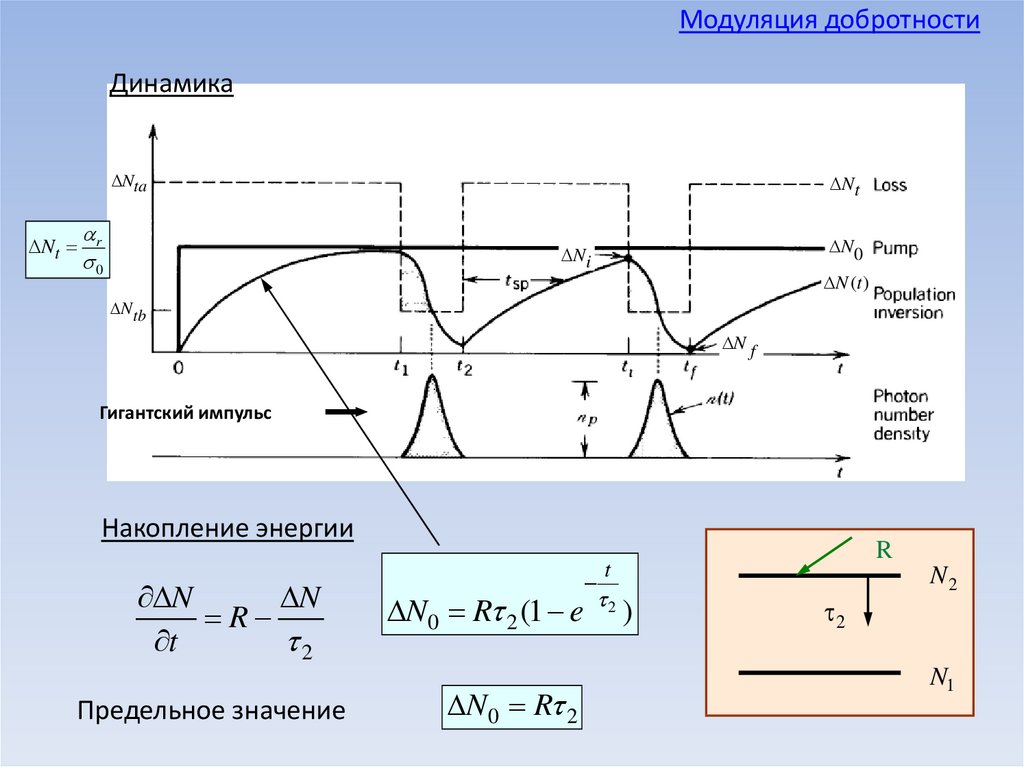
Модуляция добротностиДинамика
Nta
Nt =
r
0
N t
N0
N i
N (t )
Ntb
N f
Гигантский импульс
Накопление энергии
N
N
=R
t
2
Предельное значение
N 0 = R 2 (1 e
N 0 = R 2
R
t
2
)
2
N2
N1
32.
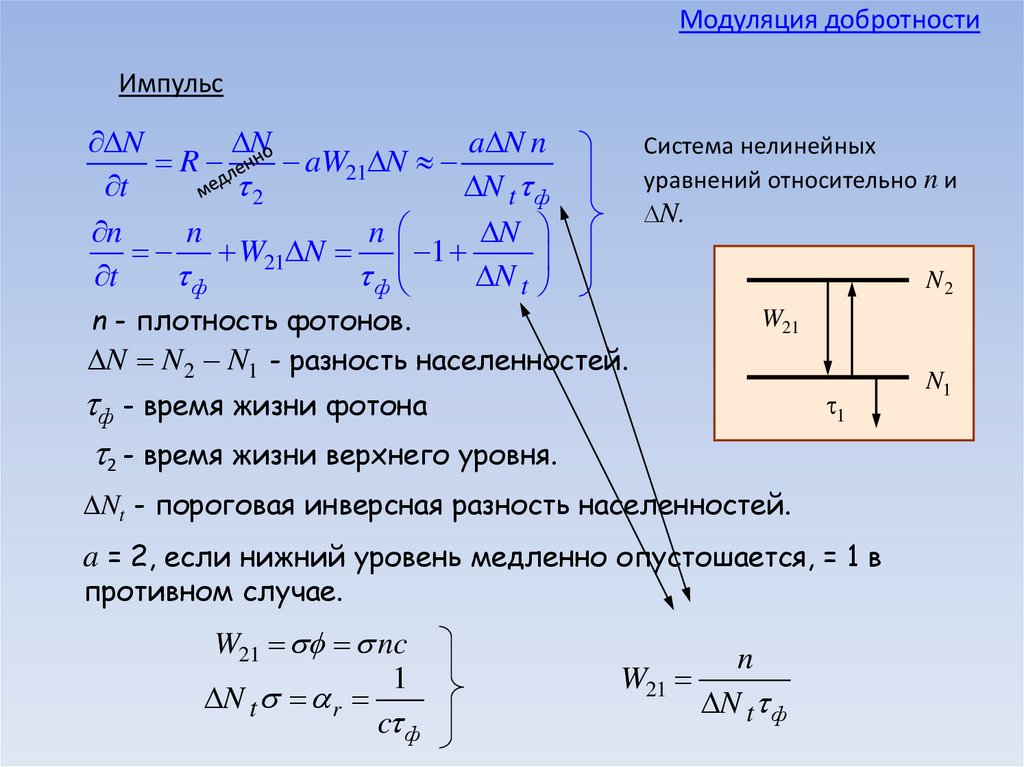
Модуляция добротностиИмпульс
N
N
a N n
=R
aW21 N
t
2
N t ф
n
n
n
N
= W21 N = 1
t
ф
ф
N t
Система нелинейных
уравнений относительно n и
N.
n - плотность фотонов.
N = N 2 N1 - разность населенностей.
N2
W21
ф - время жизни фотона
2 - время жизни верхнего уровня.
1
Nt - пороговая инверсная разность населенностей.
a = 2, если нижний уровень медленно опустошается, = 1 в
противном случае.
W21 = = nc
1
N t = r =
c ф
W21 =
n
N t ф
N1
33.
Модуляция добротностиДелим второе уравнение на первое:
n
1 Nt
n N
=
=
1
t
t
N a N
Начальные условия:
t = ti , n = 0, N = Ni
Решение:
N
1
Nt
n=
1 d N
a N N
i
1
N 1
n = Nt ln
( N Ni )
a
Ni a
34.
Модуляция добротностиВыходная мощность (в любой момент времени)
1
1
Pout = h out S = h T S = h Tnc S =
2
2
c
c
1
= h Tn
SL = h nV T
h nV
2L
2L
ф
Физический смысл множителей
h
- энергия фотона.
nV
1
- количество фотонов в резонаторе.
c
=T
ф
2L
- относительные потери энергии на высвечивание
за единицу времени.
35.
Модуляция добротностиПиковая выходная мощность
Максимум мощности (то есть точка экстремума) соответствует
Pout
c n
= h V T
t
2 L t
Используя балансное уравнение для n:
находим, что в максимуме
Подстановка
Pout
= 0.
t
n n
N
= 1
t ф
N t
=0
N = N t
N = N
в выражение
для n
t
1
N 1
с учетом того, что
N i N t
n = Nt ln
( N Ni )
1
c
1
1
1
a
N
a
и = h N i V T
Pout max
h N i V
дает
nmax i= N i
a
2L a
ф
a
Оценки показывают, что
Pout max
Pout непр
2 10 3 10 5
3
5
8
10
10
ф 10 10 9
36.
Модуляция добротностиЭнергия импульса
tf
tf
c
E = Pout dt = h T
V n(t ) dt
2L t
t
tf
i
N
n(t ) dt =
ti
i
f
Ni
dt
n( N )
d N =
d N
d N
a N n
=
dt
N t ф
tf
n(t ) dt =
ti
Nt ф
a
N
f
1
n( N ) d N d N
Ni
dt
- балансное уравнение
Ni
ln
N f
Если воспользоваться выражением для n и подставить в него
котором n=0, то для логарифма получим
Ni Ni N f Ni
ln
=
N f
Nt
Nt
N, при
= N f
37.
Модуляция добротностиОкончательно
1
c
E = h N i V T ф = Pout max ф
a
2L
Если предположить, что потери резонатора в основном связаны с выходным
излучением, то есть
2L
ф
Tc
то
1
E = h N iV
a
Эта формула показывает, что практически вся запасенная энергия в инверсной
населенности переходит в энергию импульса.
38.
Модуляция добротностиДлительность импульса
можно грубо оценить как отношение энергии импульса к пиковой мощности
tимп
E
Pout max
= ф
наносекунды
n(t )
N t
N i
= 10
N t
Численные расчеты
формы импульса
t
ф
39.
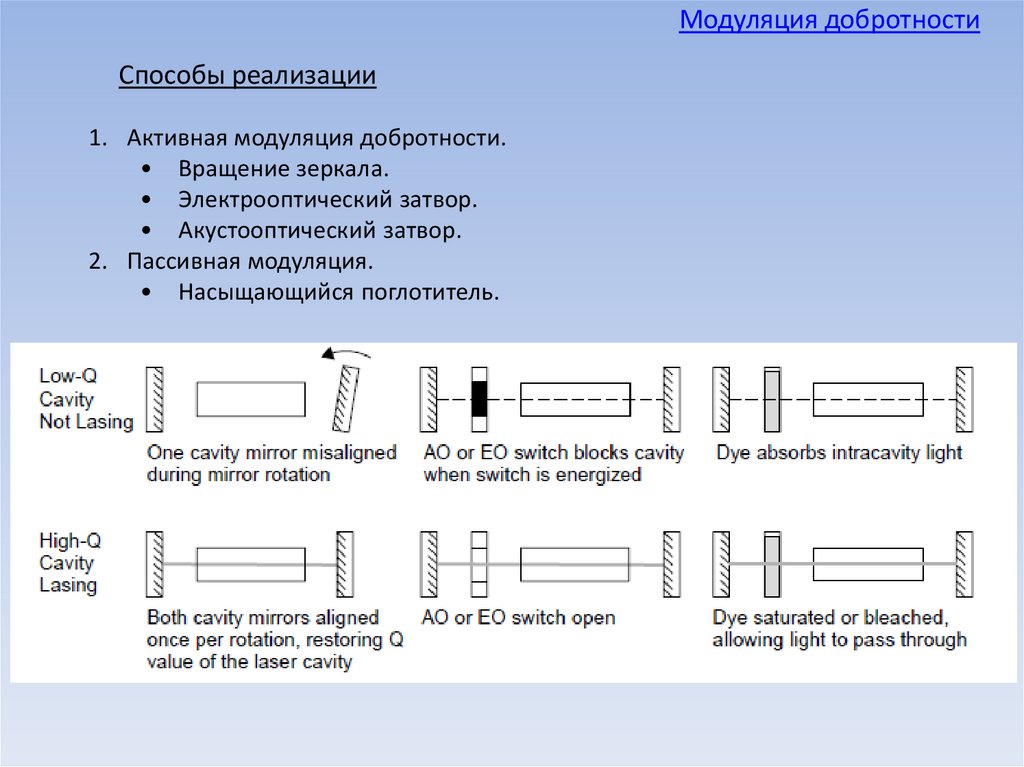
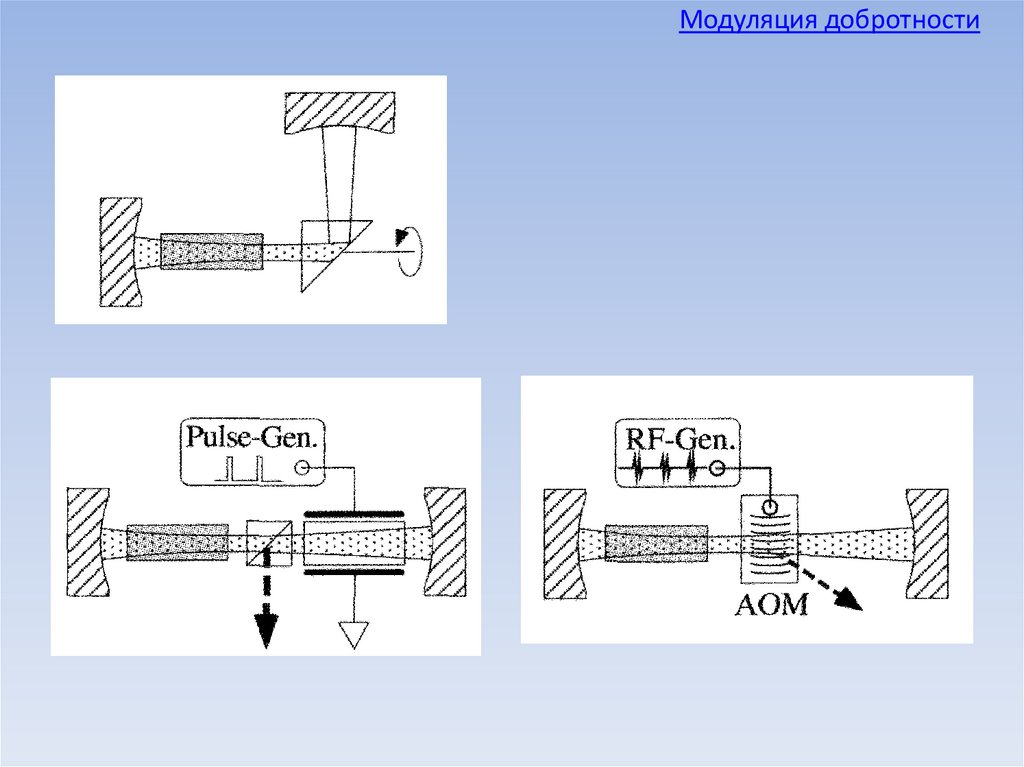
Модуляция добротностиСпособы реализации
1. Активная модуляция добротности.
• Вращение зеркала.
• Электрооптический затвор.
• Акустооптический затвор.
2. Пассивная модуляция.
• Насыщающийся поглотитель.
40.
Модуляция добротности41.
Модуляция добротности42.
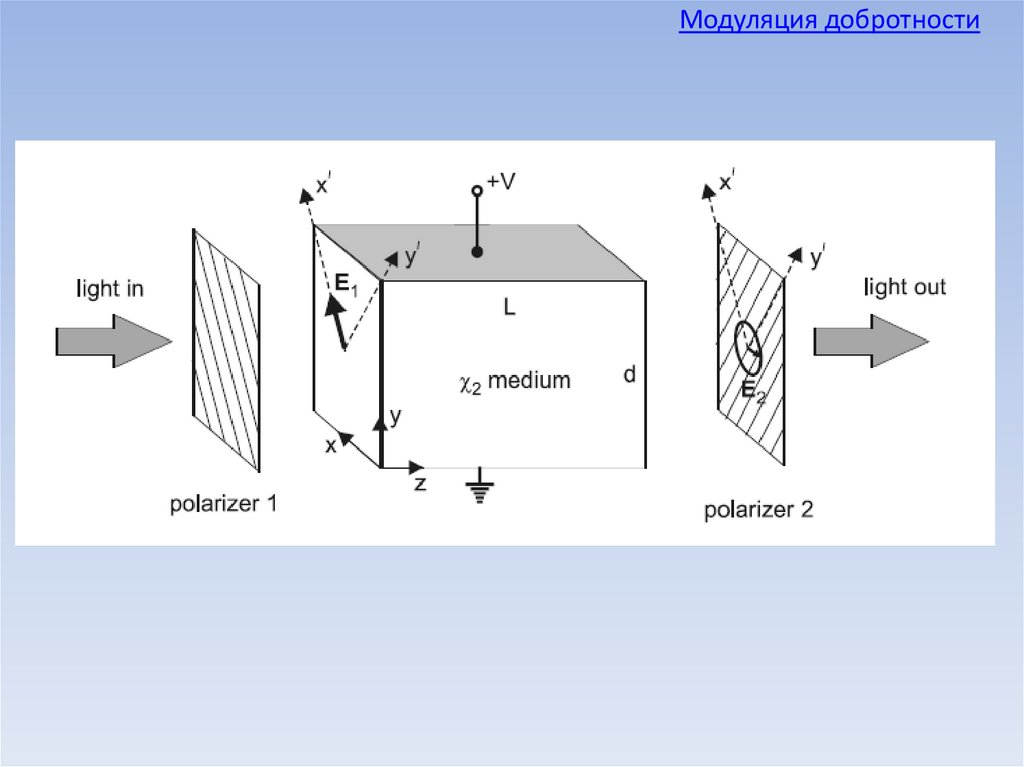
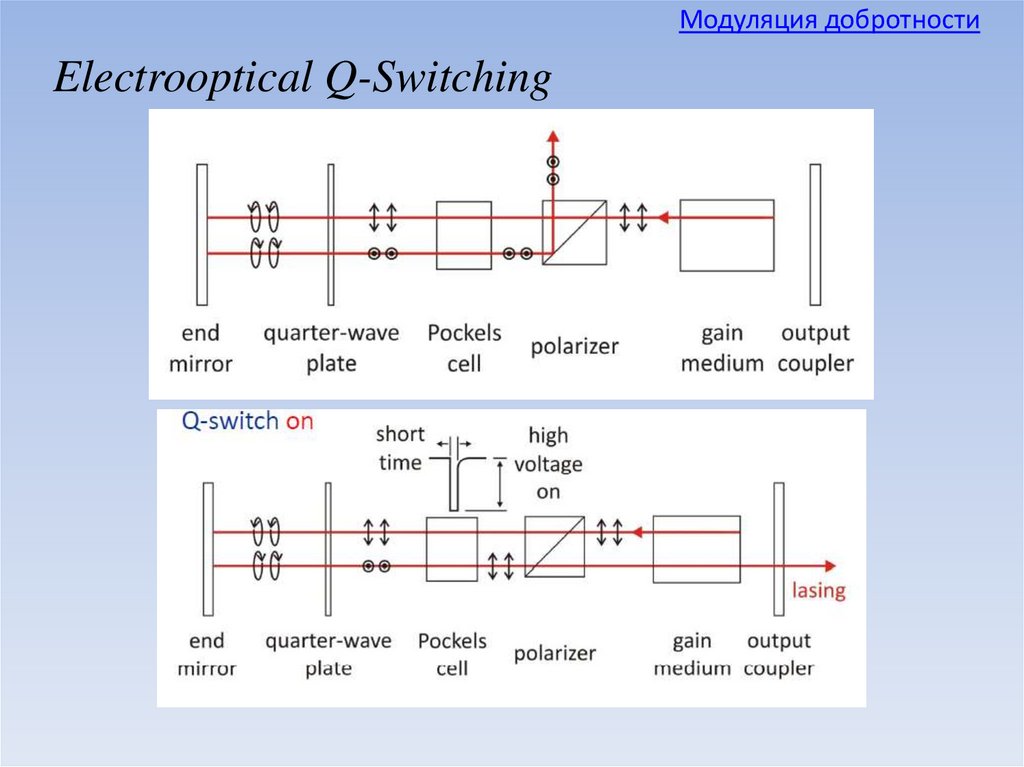
Модуляция добротностиElectrooptical Q-Switching
43.
Модуляция добротностиAcoustooptic Q-Switches
Bragg diffraction
- угол падающего пучка.
When this equation is satisfied, reflected waves from each parallel plane will be
separated by a phase shift of exactly 2 , so that constructive interference takes
place.
44.
Модуляция добротностиAcoustooptic Q-Switches
Raman–Nath diffraction
Raman–Nath diffraction occurs
when the incoming beam is
aligned perpendicular to the
alternating layers, which now act
like parallel slits in a transmission
diffraction grating.
45.
Модуляция добротностиВыводы
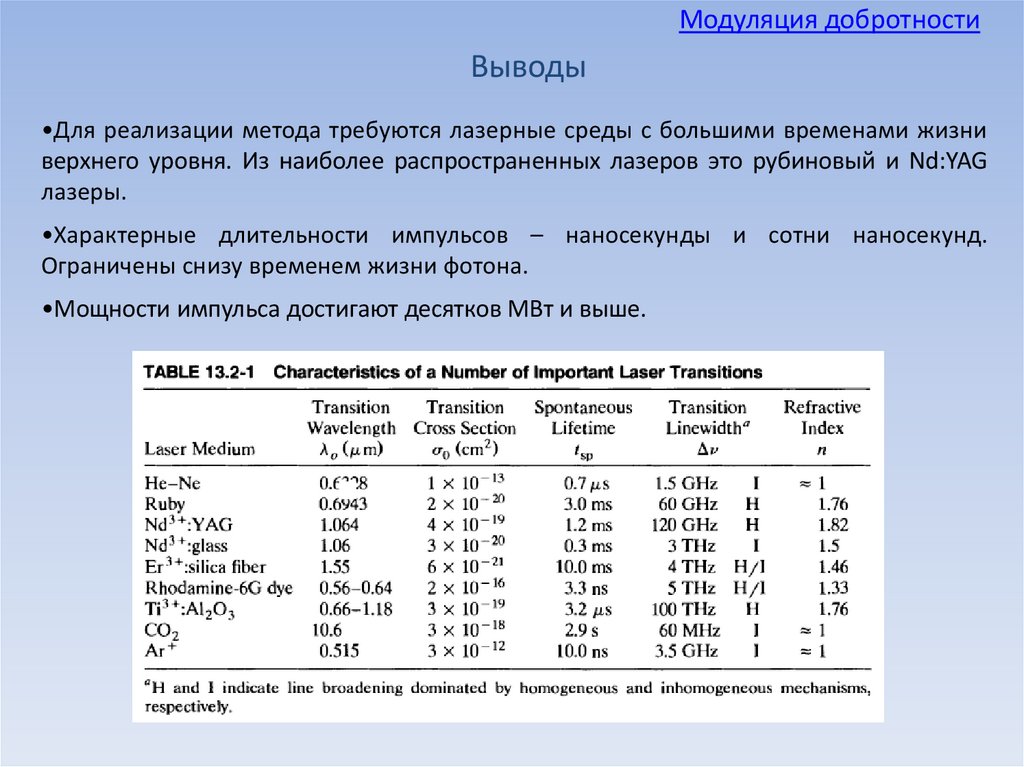
•Для реализации метода требуются лазерные среды с большими временами жизни
верхнего уровня. Из наиболее распространенных лазеров это рубиновый и Nd:YAG
лазеры.
•Характерные длительности импульсов – наносекунды и сотни наносекунд.
Ограничены снизу временем жизни фотона.
•Мощности импульса достигают десятков МВт и выше.
































 physics
physics








