Similar presentations:
Поляризация света. Световой вектор. Естественный и поляризованный свет. Лекция 11
1. ЛЕКЦИЯ 11
2. ПОЛЯРИЗАЦИЯ СВЕТА
3. СВЕТОВОЙ ВЕКТОР. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ
4.
Согласно электромагнитной теории света Максвелла :СВЕТ – представляет собой электромагнитные волны
распространяющиеся в среде с конечной скоростью ,
(переменное магнитное поле всегда связано с порождаемым им электрическим полем, и наоборот, то есть
электрическое и магнитное поле непрерывно связаны
друг с другом, и они образуют единое электромагнитное поле).
y
Следствием теории Максвелла явля
ется поперечность электромагнитE
ных волн: векторы E и H напряженностей электрического и магнитного полей взаимно перпенди- z
x
кулярны, и перпендикулярны ско- H
рости распространения волны .
5.
Векторы E , H и образуют правовинтовую систему, векторы E и H колеблются в одинаковых фазах, причем ,мгновенные соотношения значений E и H в любой
точке связаны соотношением:
0 E 0 H
Для описания закономерностей поляризации света
достаточно знать поведение лишь одного из векторов
E и H . Традиционно, все рассуждения ведутся относительно светового вектора – вектора напряженности
электрического поля E (это обусловлено тем, что при
действии света на вещество основное значение имеет
электрическая составляющая поля волны, действующая на электроны в атомах вещества).
6. ПОЛЯРИЗАЦИЯ
Свет представляет собой суммарное электромагнитноеизлучение множества атомов. Атомы излучают световые волны независимо друг от друга, поэтому световая волна в целом, характеризуется всевозможными
равновероятными колебаниями светового вектора.
В данном случае равномерное распределение
векторов E объясняется большим числом
атомарных излучателей, а равенство ампли- E
тудных значений векторов E одинаковой (в среднем)
интенсивностью излучения каждого из атомов. Свет
со всевозможными равновероятными ориентациями
вектора E называется - ЕСТЕСТВЕННЫМ, а в котором
направления световых колебаний каким либо образом
упорядоченны – ПОЛЯРИЗОВАННЫМ.
7.
• ЕСТЕСТВЕННЫЙ СВЕТ – колебания светового вектора равновероятны по всемнаправлениям
• ЧАСТИЧНО ПОЛЯРИЗОВАННЫЙ СВЕТ – Естественный
появляется (в результате внешнего воз- свет
действия) преимущественное (но не
единственное) направление колебаний
Частично поляривектора E .
зованный свет
• ПЛОСКОПОЛЯРИЗОВАННЫЙ (ЛИНЕЙНО
ПОЛЯРИЗОВАННЫЙ) СВЕТ – свет , в ко- Плоскополяризо(линейно
тором вектор E колеблется только в ванный
поляризованный)
одном направлении перпендикуляр- свет
ном .
8.
Плоскость , проходящая через направление колебанийсветового вектора плоскополяризованной волны и направление распространения этой волны, называется
ПЛОСКОСТЬЮ ПОЛЯРИЗАЦИИ.
ЭЛЛИПТИЧЕСКИ ПОЛЯРИЗОВАННЫЙ СВЕТ – свет,
для которого вектор E , изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости перпендикулярной лучу света.
Предельные случаи эллиптически поляризованного
света это плоскополяризованный свет, и циркульно
поляризованный (поляризованный по кругу) свет.
9. СТЕПЕНЬ ПОЛЯРИЗАЦИИ
СТЕПЕНЬЮ ПОЛЯРИЗАЦИИ называется величина:I max I min
P
I max I min
Где: I max и I min – соответственно максимальная и минимальная интенсивности частично поляризованного
света, пропускаемого анализатором .
Для естественного света:
I max I min P 0
Для полностью поляризованного света:
I min 0 P 1
10. ПОЛЯРИЗАТОРЫ И АНАЛИЗАТОРЫ. ЗАКОН МАЛЮСА
11.
Естественный свет можно преобразовать в плоскополяризованный с помощью ПОЛЯРИЗАТОРОВ, пропускающихколебания только определенного направления (например пропускающие колебания параллельные главной оптической плоскости поляризации и полностью задерживающие колебания перпендикулярные этой плоскости).
Деятельность поляризаторов основана на поляризации света при его отражении и преломлении на границе раздела
двух диэлектрических сред, а так же на эффекте двойного лучепреломления. В качестве поляризаторов могут
быть использованы некоторые кристаллы, например турмалин. При превращении естественного света в плоскополяризованный, его интенсивность уменьшается в два
раза:
1
I пол I ест
2
12. АНАЛИЗАТОРЫ
Для определения характера и степени поляризации используют АНАЛИЗАТОРЫ, в их роли могут выстутать теже устройства, которые использовались в качестве поляризаторов. При попадании на анализатор поляризованного света, если угол между направлением колебания света рр´ и оптической осью аа´ анализатора ,
то соотношение между амплитудами падающего поляризованного света Ap и выходящего анализированного света Aa (без учета потерь света в веществе аналиp
затора) будет равно:
a
Ip I
a
A p Aa
Aa A p cos
a
p
13. ЗАКОН МАЛЮСА
Так как амплитуда света A (она же E ) пропорциональнаквадрату интенсивности света I 2 ,то по ЗАКОНУ МАЛЮСА :
I a I p cos 2
Пропустим естественный свет интенсивностью I e через
две одинаковые пластины, угол между оптическими
поляризатор анализатор
осями которых .
Потерь интенсивности света внутри пластин, из за свойств
материалов нет.
I ест
I ест
Ip
2
I ест 2
I a I p cos
cos
2
2
14.
При прохождении светаполяризатор анализатор
через первую пластину, служащую поляризатором, естественный
свет поляризуется, и I ест
I ест
I ест
2
совершает колебания
I a I p cos
cos 2
Ip
2
2
в плоскости, проходящей через оптическую ось первого кристалла. Интенсивность поляризованного света:
Ip
I ест
2
При попадании уже поляризованного света на вторую
пластину, она служит уже анализатором, и интенсивность света после её прохождения определяется законом Малюса: I I cos 2 I ест cos 2
a
p
2
15.
Если на пластину служащую анализатором падает естественный свет, то она выступает в качестве поляризатора.Если у анализатора оптическая ось параллельна оптической оси поляризатора ( 0 ) то интенсивность света
на выходе:
I ест
I ест
2
Ia
cos 0
2
2
Если анализатор и поляризатор скрещены ( 90 ) то:
I ест
Ia
cos 2 90 0
2
16. ПОЛЯРИЗАЦИЯ СВЕТА ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ СВЕТА НА ГРАНИЦЕ ДВУХ ДИЭЛЕКТРИКОВ
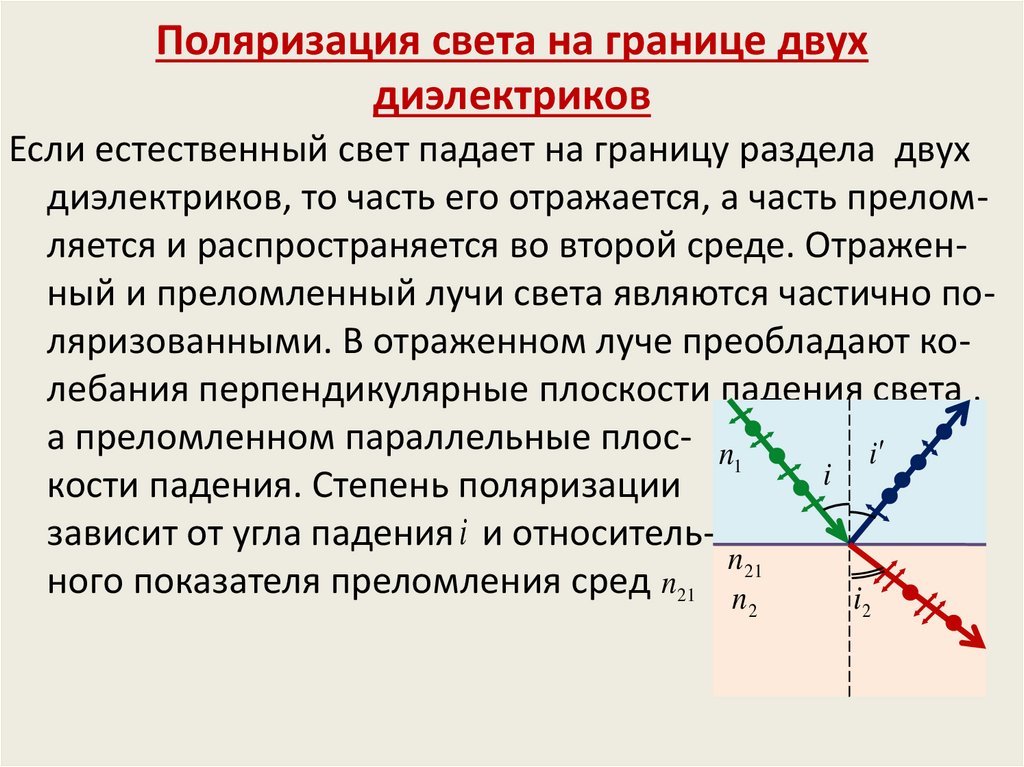
17. Поляризация света на границе двух диэлектриков
Если естественный свет падает на границу раздела двухдиэлектриков, то часть его отражается, а часть преломляется и распространяется во второй среде. Отраженный и преломленный лучи света являются частично поляризованными. В отраженном луче преобладают колебания перпендикулярные плоскости падения света ,
а преломленном параллельные плос- n
i
1
i
кости падения. Степень поляризации
зависит от угла падения i и относительn21
ного показателя преломления сред n21 . n
i
2
2
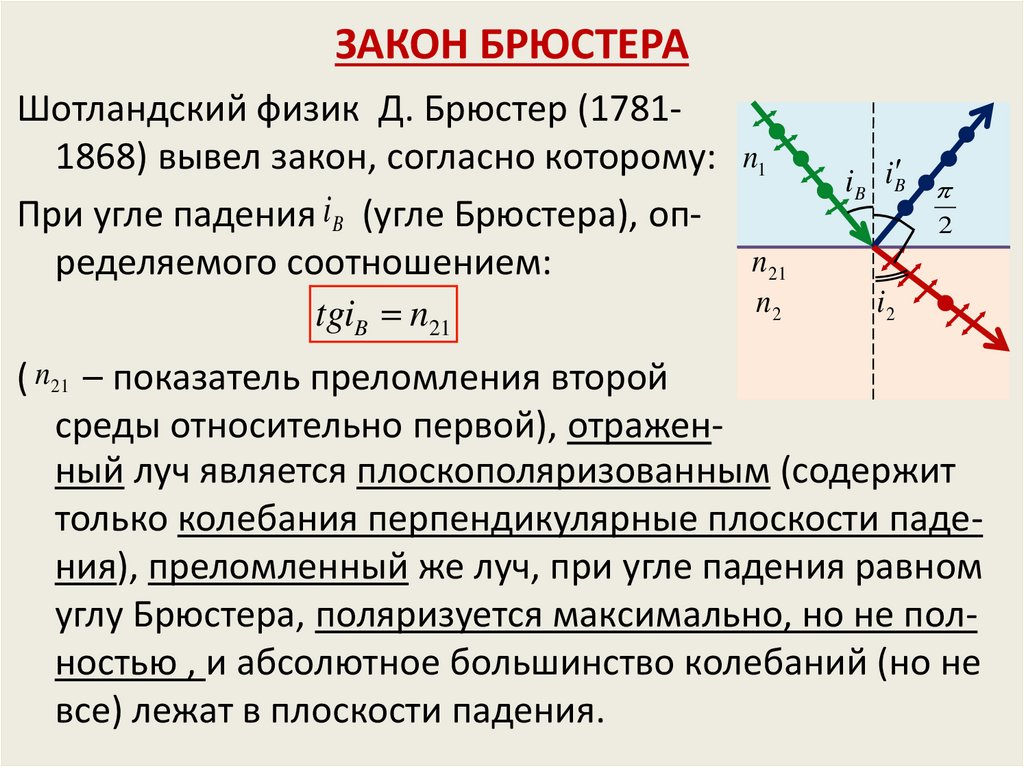
18. ЗАКОН БРЮСТЕРА
Шотландский физик Д. Брюстер (17811868) вывел закон, согласно которому: n1При угле падения i B (угле Брюстера), опn21
ределяемого соотношением:
n2
tgiB n21
i B i B
2
i2
( n21 – показатель преломления второй
среды относительно первой), отраженный луч является плоскополяризованным (содержит
только колебания перпендикулярные плоскости падения), преломленный же луч, при угле падения равном
углу Брюстера, поляризуется максимально, но не полностью , и абсолютное большинство колебаний (но не
все) лежат в плоскости падения.
19.
Если свет падает на границу раздела двух сред под угломБрюстера, падающий, отраженный и преломленный
лучи лежат в одной плоскости. Угол между отраженным и преломленным лучами равен 90°
sin i B
tgiB
cos i B
sin i B
n21
sin i2
i B i B
cos i B sin i2 i B i2 i B i2
2
Степень поляризации преломленного луча света может
быт многократно повышена многократным преломлением при условии падения луча света каждый раз под
углом Брюстера. Для этого собирается совокупность
наложенных друг на друга пластинок (стопа). После
нескольких преломлений, свет выходит из системы
практически полностью поляризованным.
20. ДВОЙНОЕ ЛУЧЕПРЕЛОМЛЕНИЕ
21.
Большинство кристаллов оптичесeки анизотропно (не изотропно),
o
иобладают свойством двойного
лучепреломления, то есть раздваивания каждого падающего на них светового пучка, (явление обнаружено впервые в 1669 г. Э.Бартолином для исландского шпата СаСО₃).
Если на толстый кристалл исландского шпата направить
узкий пучок света, то из кристалла выйдут два разделённых, параллельных друг другу и падающему лучу
световых луча.
Даже если первичный луч будет падать нормально, преломленный будет разделен на два, один из них является продолжением исходного (обыкновенный луч о), а
второй отклоняется (необыкновенный луч е).
22.
Единственное направление вдоль коOe
торого двойного лучепреломления
не происходит называется оптичесo
кой осью кристалла. Это именно НАПРАВЛЕНИЕ, и, любая прямая, проходящая параллельно ей является опO
тической осью кристалла.
Кристаллы, в зависимости от типа их симметрии бывают
одноосные или двухосные. Плоскость проходящая через направление луча света и оптическую ось кристалла
называется главной плоскостью (главным сечением).
Вышедшие из кристалла лучи будут плоско поляризованы во взаимно перпендикулярных плоскостях. Колебания светового вектора E для о перпендикулярны
главной плоскости, а для е лежат в главной плоскости.
23. СКОРОСТЬ РАСПРОСТРАНЕНИЯ СВЕТА В СРЕДЕ
Неодинаковое преломление о и е, указывает на различные для этих лучей показатели преломления n o и ne , атак же скорости распространения o c no и e c ne .
При любом направлении о , колебания светового вектора E перпендикулярны оптической оси кристалла и
обыкновенный луч о распространяется по всем направлениям с одинаковой скоростью o , показатель преломления n o величина постоянная.
Для е угол между направлениями колебания и оптической осью отличен от прямого, и зависит от направления луча, поэтому е распространяется по различным
направлениям с различными скоростями. Значит, показатель преломления необыкновенного луча является переменной величиной, зависящей от направления
24.
луча. Из этого следует, что о подчиняется закону преломления, а для е в кристалле этот закон не соблюдается. После выхода из кристалла оба луча и о и е, посвоим свойствам практически не отличаются.
В случае распространения луча вдоль оптической оси
o e и no ne , то есть вдоль оптической оси существует только одна скорость распространения света.
Различие в o и e , для всех направлений кроме
оптической оси, и обуславливает явление двойного
лучепреломления в одноосных кристаллах.
25.
На рисунке представлено распространеПоложительныйодноосный
ние обыкновенного и необыкновенного
кристалл
лучей о и е в кристалле (главная оптиO
ческая ось совпадает с плоскостью чертежа, ОО´ - направление оптической оси)
S
Волновой поверхностью о ( распространя o
ющегося со скоростью o const ) являетe
ся сфера , а для е ( e const )– эллипсоид
O´
вращения.
Отрицательный
одноосный
S – точка внутри кристалла, являющаяся
кристалл
точечным источником света.
O
Если e 0 ne n0 , то эллипсоид е вписан
S
o e
в сферу о (эллипсоид вытянут относительно оптической оси), и одноосный
O´
кристалл называется положительным.
26.
Наоборот, если e 0 ne n0 , то эллипсоид описан вокруг сферы (эллипсоид скоростей растянут в направлении, перпендикулярном оптической оси) и одноосный кристалл называется отрицательным.(исландский шпат – отрицательный кристалл).
27. ПОЛЯРИЗАЦИОННЫЕ ПРИЗМЫ И ПОЛЯРОИДЫ
В основе работы поляризационных приспособлений,служащих для получения поляризованного света лежит явление двойного лучепреломления. Наиболее
часто для этого применяются призмы и поляроиды.
По типу призмы делятся на:
• Призмы дающие только плоскополяризованный луч
(поляризационные призмы)
• Призмы дающие два поляризованных во взаимоперпендикулярных плоскостях луча (двоякопреломляющие призмы)
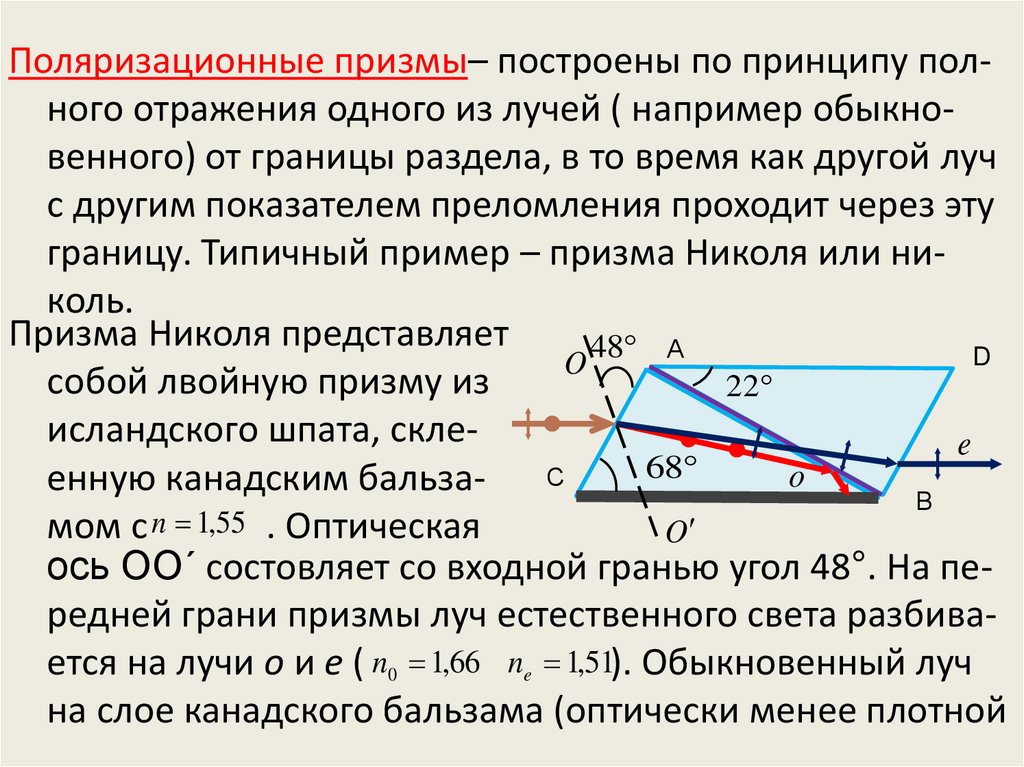
28.
Поляризационные призмы– построены по принципу полного отражения одного из лучей ( например обыкновенного) от границы раздела, в то время как другой лучс другим показателем преломления проходит через эту
границу. Типичный пример – призма Николя или николь.
Призма Николя представляет
D
O 48 А
собой лвойную призму из
22
исландского шпата, склеe
68
С
o
енную канадским бальзаВ
мом с n 1,55 . Оптическая
O
ось ОО´ состовляет со входной гранью угол 48°. На передней грани призмы луч естественного света разбивается на лучи о и е ( n0 1,66 ne 1,51). Обыкновенный луч
на слое канадского бальзама (оптически менее плотной
29.
среде) испытывает полное отражение, а затем поглощается полностью зачернённой поверхностью CВ.Необыкновенный луч – выходит из призмы параллельно
падающему лучу. Незначительно смещенный относительно него из-за преломления на наклонных гранях
АС и ВD.
Двоякопреломляющие призмы – используют различие в
показателях преломления о и е лучей, что бы развести
их подальше друг от друга( например призмы из шпата и стекла, для них обыкновенный луч о преломляется в шпате и стекле два раза и сильно отклоняется, а
необыкновенный е при специальном подборе стекла с
показателем преломления nc ne проходит призму
почти без отклонения.
30.
Двоякопреломляющие призмы обладают свойством дихроизма, то есть различного поглощения света, в зависимости от ориентации электрического вектора световой волны, и называются дихроичными кристаллами.Пример – турмалин, при слое пластинки 1 мм , из-за
сильного селективного (выборочного) поглощения
проходит только необыкновенный луч е. такое различие в поглощении, зависящее, кроме того от длины
волны, приводит к тому, что при освещении дихроичного кристалла белым светом кристал по разным
направлениям оказывается различно окрашенным.
31.
Поляроиды – тонкие пленки, обладающие ярко выраженным дихроизмом и преобразующие естественныйсвет в линейно поляризованный. Типичный пример –
тонкая пленка из целлулоида с вкраплением кристаллов герапатита (сернокислого йод-хинина). При толщине пленки 0.1 мм полностью поглощает обыкновенные лучи в видимой области спектра. Степень
поляризации в полароидах сильно зависит от длины
волны падающего света.
32. ИССКУСТВЕННАЯ ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
33.
Двойное лучепреломление имеет место в естественныханизотропных средах. Однако, ещё в середине XIX в.
Было обнаружено явление фотоупругости: оптически
изотропное твердое тело, под влиянием механической
деформации, становится оптически анизотропным
(например, при одностороннем растяжении или сжатии стеклянной пластинки – она приобретает свойства
одноосного кристалла, ось которого совпадает с
направлением растяжения (сжатия)).
Данное явление носит название: ИСКУСТВЕННОЙ ОПТИЧЕСКОЙ АНИЗОТРОПИИ, то есть сообщения оптической анизотропии естественно изотропным веществам.
34.
Оптически изотропные вещества становятся оптическианизотропными под влиянием:
1. Одностороннего сжатия или растяжения (фотоупругость)(для кристаллов кубической системы, стекла…)
2. Электрического поля (эффект Керра)(для жидкостей,
газов, аморфных веществ)
3. Магнитного поля (жидкости, стекла, коллоиды)
Вещество приобретает свойства одноосного кристалла,
оптическая ось которого совпадает с направлением
деформации, электрического или магнитного полей.
35.
Мерой возникающей искуственной оптической деформации служит разность показателей преломления обыкновенного и необыкновенного лучей в направленииперпендикулярном оптической оси:
no ne k1
• Для деформации:
2
n
n
k
Е
o
e
2
• Для электрического поля:
no ne k 3 Н 2
• Для магнитного поля:
k1 k 2 k 3 – постоянные характеризующие вещество
Е, Н – напряженности электрического и магнитного
поля соответственно
36. ЭФФЕКТ КЕРРА
Жидкий или твердый изотропный диэлектрик, помещенный в достаточно сильное однородное электрическоеполе становится оптически анизотропным.
На рисунке приведена схема для наблюдения эффекта
Керра. Между поляризатором Р и анализатором А помещена ячейка Керра (кювета с жидкостью, например
с нитробензолом) в которую помещены обкладки плоского конденсатора . При отсутствии электрического
поля свет через систему не проходит. При наложении
электрического поля жидкость становится двоякопреломляющей, и при изменении разности потенциалов
Р
А
37.
между электродами меняется анизотропия вещества,а значит и интенсивность света прошедшего через
анализатор. На пути l между о и е лучами возникает
оптическая разность хода l n0 ne k 2 E 2 l , и разность
фаз
2 2 BlE 2
Где: k 2 B – постоянная Керра
Эффект Керра объясняется различной поляризуемостью
молекул жидкости по разным направлениям. Это явление безинерционно, то есть переход вещества в
анизотропное состояние и обратно занимает примерно 10¯¹⁰с. Ячейка Керра создает между обыкновенным и необыкновенным лучами сдвиг фаз.
38.
КВАНТОВАЯ ПРИРОДАИЗЛУЧЕНИЯ
39. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
40. ХАРАКТЕРИСТИКИ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
41. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Нагретые до достаточно высоких температур тела светятся. Свечение обусловлено ТЕМПЕРАТУРНЫМ ТЕПЛОВЫМ ИЗЛУЧЕНИЕМ. Данное излучение является самымраспространенным в природе, совершается за счет теплового движения атомов и молекул вещества ,(то есть
за счет внутренней энергии), и свойственно всем телам при температуре выше 0К. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких в основном
длинные (инфракрасные).
Тепловое излучение единственный вид излучения которое может быть РАВНОВЕСНЫМ , (то есть при определенных условиях тело в единицу времени может поглощать столько же энергии, сколько и излучать).
42.
Если равновесие между телом и излучением по какой топричине нарушено , и тело излучает больше энергии
чем поглощает , (или наоборот), то, со временем, температура тела будет понижаться (или, соответственно,
повышаться). В результате будет уменьшаться (при нагревании возрастать) количество излучаемой телом
энергии, пока не установится равновесие.
Все другие виды излучения, кроме теплового, НЕРАВНОВЕСНЫЕ.
43. ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА
Количественной характеристикой теплового излученияслужит СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ
СВЕТИМОСТИ (ИЗЛУЧАТЕЛЬНОСТЬ) ТЕЛА.
ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА R ,T – мощность излучения с
единицы площади поверхности тела, в интервале частот единичной ширины.
R ,T
dW изл
, d
dW изл
, d
d
– энергия электромагнитного излучения,
испускаемого за единицу времени (мощность
излучения), с единицы площади поверхности тела, в
интервале частот от до d .
Дж
Единица измерения излучательности тела: м 2 с
44.
Записанную формулу можно представить в виде функциидлины волны:
dW изл
, d R ,T d R ,T d
Так как c , то
d
c
2
2
d
c
Знак минус показывает на то, что с ростом одной из величин ( или ) другая будет убывать. Поэтому, в дальнейшем знак минус можно опускать. Значит :
2
R ,T R ,T
c
Зная спектральную плотность энергетической светимости
можно определить интегральную энергетическую
светимость (интегральную излучательность) или энергетическую светимость тела: R R d
T
0
,T
45. СПЕКТРАЛЬНАЯ ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ
Способность тел поглощать падающее на них излучениехарактеризуется: СПЕКТРАЛЬНОЙ ПОГЛОЩАЮЩЕЙ
СПОСОБНОСТЬЮ :
A ,T
dW погл
, d
dW , d
Спектральная поглощающая способность показывает какая доля энергии, приносимой за единицу времени на
единицу площади поверхности тела падающими на
неё электромагнитными волнами с частотами от до
d поглощается телом. A ,T – величина безразмерная.
A ,T и R ,T зависят от природы тела, его температуры, и,
при этом различаются для излучений с различными
46.
частотами. Поэтому эти величины относят к определенным температурам T и частотам (точнее к максимально узкому интервалу частот от до d ) .47. АБСОЛЮТНО ЧЕРНОЕ ТЕЛО
Тело, способное поглощать полностью, при любой температуре всё падающее на него излучение называется:АБСОЛЮТНО ЧЕРНЫМ ТЕЛОМ. Спектральная поглощательная способность черного тела для всех частот и
температур равна единице: Aч 1 . Абсолютно черных
тел в природе нет, но существуют тела по своим свойствам достаточно близкие к ним.
Хорошей моделью черного тела является замкнутая полость, внутренняя поверхность которой зачернена. Луч
• света попавший внутрь неё испытывает многократные отражения от стенок, в результате
интенсивность вышедшего луча будет близка к нулевой.
,T
48. СЕРОЕ ТЕЛО
СЕРОЕ ТЕЛО – тело, поглощательная способность которого меньше единицы, но одинаково для всех частоти зависит только от температуры, материала и состояния поверхности тела.
A c,T AT const 1
Рассмотрим законы, которым подчиняется тепловое
излучение.
49. ЗАКОН КИРХГОФА
50.
Опираясь на второе начало термодинамики, и анализизруя условия равновесного излучения Кирхгоф установил количественную связь между спектральной плотностью энергетической светимости и спектральнойпоглощательной способностью тел.
Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности
НЕ ЗАВИСИТ от природы тела, оно является для всех
тел универсальной функцией частоты (длины волны) и
температуры.
R ,T
A ,T
r ,T
Так как для абсолютно черного тела Aч 1 то получается
,T
R ч,T r ,T
51. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ СВЕТИМОСТИ ЧЕРНОГО ТЕЛА
r ,T – УНИВЕРСАЛЬНАЯ ФУНКЦИЯ КИРХГОФА или спект-ральная плотность энергетической светимости черного тела .
По закону Кирхгофа для всех тел отношение R ,T к A ,T равно спектральной плотности энергетической светимости
черного тела при той же температуре и частоте.
Выражению энергетической светимости тела можно
придать вид:
RT A ,T r ,T d
Для серого тела:
0
R Tc AT r ,T d AT Re
0
Re – энергетическая светимость черного тела
Re r ,T d
0
52.
Из закона Кирхгофа следует что:1. R ,T любого тела, в любой области спектра, всегда
меньше r ,T (при тех же значениях и T ). Так как A 1
то R ,T r ,T .
2. Если тело не поглощает электромагнитной волн какой либо частоты, то оно их и не излучает, так как
при A 0 будет R ,T 0 .
Закон Кирхгофа описывает только тепловое излучение.
Излучение которое не подчиняется закону Кирхгофа
не является тепловым.
,T
,T
53. ЗАКОН СТЕФАНА-БОЛЬЦМАНА. ЗАКОН СМЕЩЕНИЯ ВИНА
54. ЗАКОН СТЕФАНА-БОЛЬЦМАНА
Спектральная плотность энергетической светимости черного тела Re является универсальной функцией, и нахождение её явной зависимости от частоты (длиныволны) и температуры является важной задачей теории теплового излучения.
Й. Стефан анализируя экспериментальные данные (1879)
и Л. Больцман применяя термодинамический метод
(18840 установили зависимость энергетической светимости Re от температуры:
Re T 4
Энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической
температуры.
55.
5,67 108
Вт
– постоянная Стефана-Больцмана
2
4
м К
Для серого тела закон Стефана-Больцмана имеет вид:
М e АT T 4
М e – энергетическая светимость серого тела
АT
– коэффициент теплового излучения серого тела
56. ЗАКОН СМЕЩЕНИЯ ВИНА
Закон Стефана-Больцмана определяя зависимость Re от Тнет дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных данных о
2
зависимости функции r ,T от длины волны ( r ,T r ,T c
- спектральная плотность энергетической светимости
черного тела для длин волн) при различных температурах, следует что распределение энергии в спектре
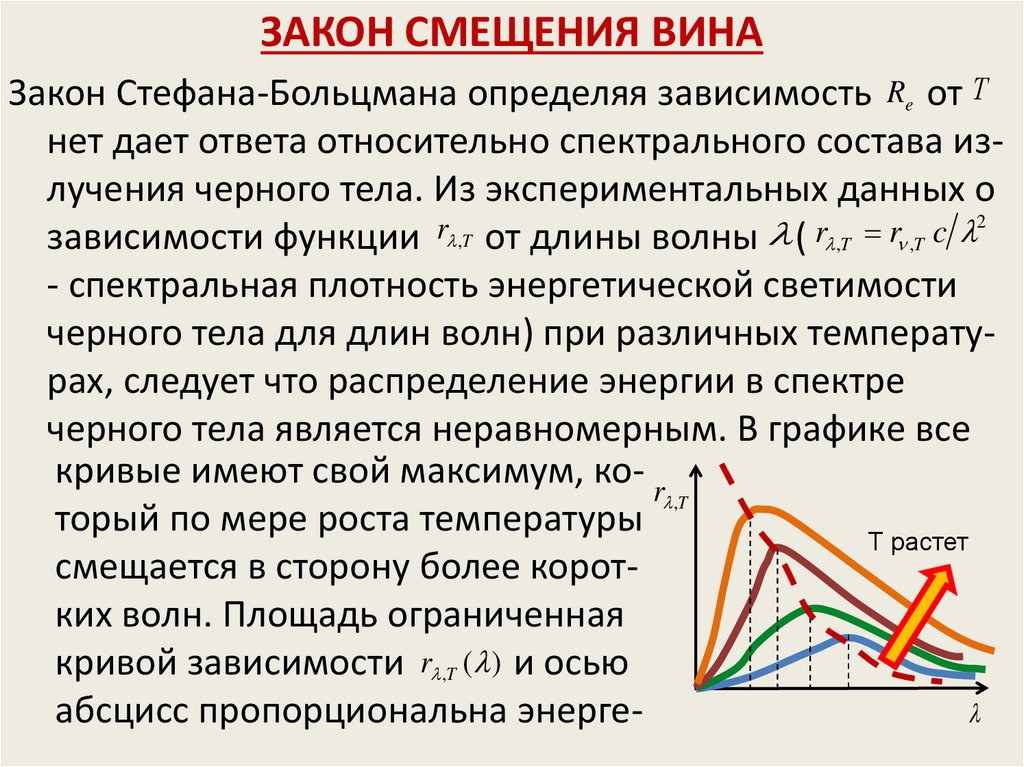
черного тела является неравномерным. В графике все
кривые имеют свой максимум, ко- r
,T
торый по мере роста температуры
Т растет
смещается в сторону более коротких волн. Площадь ограниченная
кривой зависимости r ,T ( ) и осью
абсцисс пропорциональна энерге
57.
тической светимости Re черного тела, и , по законуСтефана-Больцмана четвертой степени температуры.
В.Вин установил зависимость длины волны max , соответствующей максимуму функции r ,T от температуры Т.
ЗАКОН СМЕЩЕНИЯ ВИНА:
b
max
T
Длина волны соответствующая максимальной плотности
энергетической светимости r ,T черного тела, обратно
пропорциональна его термодинамической температуре.
b 2.9 10 3 м К – постоянная Вина
58.
Закон смещения Вина показывает смещение положениямаксимума функции r ,T по мере возрастания температуры в области коротких длин волн.
Закон Вина объясняет, почему при понижении температуры нагретых тел цвет переходит от белого к красному.
Законы Стефана-Больцмана и Вина – частные законы, которые не дают общей картины распределения энергии
по частотам при разных температурах.
59. ФОРМУЛА РЭЛЕЯ-ДЖИНСА. ФОРМУЛА ПЛАНКА. КВАНТЫ
60. ФОРМУЛА РЭЛЕЯ-ДЖИНСА
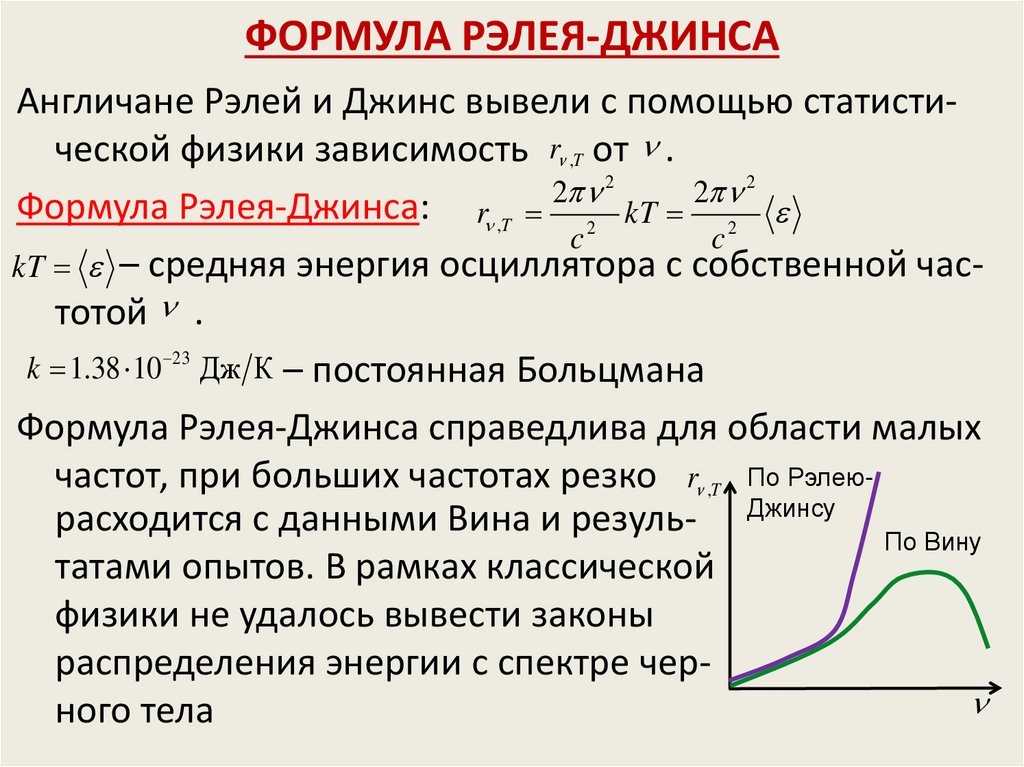
Англичане Рэлей и Джинс вывели с помощью статистической физики зависимость r ,T от .2
2
2
2
Формула Рэлея-Джинса: r ,T 2 kT 2
c
c
kT – средняя энергия осциллятора с собственной частотой .
k 1.38 10 23 Дж К – постоянная Больцмана
Формула Рэлея-Джинса справедлива для области малых
частот, при больших частотах резко r ,T По Рэлеюрасходится с данными Вина и резуль- Джинсу По Вину
татами опытов. В рамках классической
физики не удалось вывести законы
распределения энергии с спектре чер
ного тела
61. КВАНТОВАЯ ГИПОТЕЗА. ФОРМУЛА ПЛАНКА
Правильное, соответствующее с опытными данными,выражение для спектральной плотности энергетической светимости было найдено в 1900г. Планком.
Планк отказался от мысли что энергия любой системы
может изменятся непрерывно, то есть принимать какие угодно значения. Согласно КВАНТОВОЙ ГИПОТЕЗЕ:
Атомные осцилляторы излучают энергию не непрерывно
а определенными порциями– КВАНТАМИ , причем,
энергия кванта пропорциональна частоте колебания:
hc
0` h
0` – энергия кванта
h 6,625 10 34 Дж с – постоянная Планка
62.
Так ка излучение испускается порциями, то энергия осциллятора дискретна и кратна целому числу элементарных значений энергии 0` .nh
n 1,2,3,
Средняя энергия осциллятора:
h
e
h
kT
1
Спектральная плотность энергетической светимости
черного тела:
2 2 h
2 h 3
1
r ,T 2 h kT
c e
1
c 2 e h kT 1
63.
Планк вывел формулу для универсальной функции Кирхгофа:2 h 3
1
r ,T
c2
e h kT 1
Данная формула согласуется с экспериментальными данными по распределению энергий в спектрах излучения
черного тела, во всем интервале частот и температур.
Из формулы Планка можно вывести закон Рэлея-Джинса
для области малых частот, закон Стефана-Больцмана и
закон сохранения Вина. Зная универсальные постоянные h, k , c можно вывести постоянные Стефана-Больцмана , Вина b , и наоборот. Формула Планка не только
хорошо согласуется с экспериментальными данными, но
и содержит в себе частные законы теплового излучения,
то есть является полным решением основной задачи
теплового излучения поставленной Планком.
64. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ. ТЕПЛОВЫЕ ИСТОЧНИКИ СВЕТА
65. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ
Законы теплового излучения используются для измерения температуры раскаленных и недоступных для контактного измерения температуры тел. Методы измерения высоких температур, использующие зависимость спектральной плотности энергетической светимости тел от температуры называются ОПТИЧЕСКОЙПИРОМЕТРИЕЙ.
Приборы для измерения температуры нагретых тел по
интенсивности их теплового излучения называются –
пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел различают: радиационную, цветовую и яркостную температуры.
66. РАДИАЦИОННАЯ ТЕМПЕРАТУРА
РАДИАЦИОННАЯ ТЕМПЕРАТУРА – такая температура черного тела, при котором его энергетическая светимостьRe равна энергетической светимости RТ исследуемого
тела. В этом случае регистрируется энергетическая светимость исследуемого тела и по закону Стефана-Больцмана вычисляется его радиационная температура.
T p 4 RT
Радиационная температура тела T p всегда меньше его
истинной температуры T . Для доказательства этого
предположим что исследуемое тело является серым.
c
4
4
4
R
A
R
A
T
T
T
AT
Тогда можно представить что: T T e T
p
p
Так какAT 1 T p T истинная температура всегда выше
радиационной T p .
67. ЦВЕТОВАЯ ТЕМПЕРАТУРА
Для серых тел спектральная плотность энергетическойсветимости R ,Т AT r ,T где AT const 1. Значит распределение энергии в спектре излучения серого тела такое же,
как и в спектре черного тела имеющего ту же температуру. Поэтому к серым телам применим закон Вина, то
есть, зная длину волны соответствующую максимальной спектральной плотности энергетической светимости R ,Т исследуемого тела, можно определить его
температуру, которая называется ЦВЕТОВОЙ ТЕМПЕРАТУРОЙ: Tц b . Для серых тел цветовая температура
совпадает с истинной, а для тех тел, которые сильно отличаются от серых понятие цветовой температуры теряет смысл.
68. ЯРКОСТНАЯ ТЕМПЕРАТУРА
ЯРКОСТНАЯ ТЕМПЕРАТУРА TЯ – температура черного тела,при которой для определенной длины волны, его спектральная плотность энергетической светимости равна
спектральной плотности энергетической светимости
исследуемого тела. То есть R ,Т r ,T ( T – истинная температура тела). По закону Кирхгофа, для исследуемого
тела при длине волны : R ,T A ,T r ,T следовательно:
z
A ,T
r ,Tя
r ,T
Так как для нечерных тел A ,T 1 , то r ,Т r ,T , и значит T TЯ ,
то есть истинная температура больше яркостной.
z
69.
В качестве яркостного пирометра обычно используетсяпирометр с исчезающей нитью накала. Нить накала
подбирается так, что бы выполнялось условие R ,Т r ,T .
В этом случае изображение нити пирометра становится неразличимым на фоне поверхности раскаленного
тела, и нить «исчезает». Используя проградуированный по черному телу миллиамперметр, можно определить яркостную температуру.
Зная поглощательную способность тела при той же самой длине волны, по яркостной температуре можно
определить истинную.
Переписав формулу Планка в виде:
z
c
2 c 2 h
r ,T 2 r ,T
5
1
e
hc
kT
1
70.
r ,Tяи учитывая что A ,T r
,T
A ,T
получим:
e
e
hc
kT
hc
kTЯ
1
1
При известных A ,T и можно определить температуру
исследуемого тела.

































































 physics
physics