Similar presentations:
Комплексные числа
1. Комплексные числа
2.
Вычислите:64
256
144
6,25
900
3.
Мнимаяединица
i – начальная буква французского слова
imaginaire – «мнимый»
4. Например,
3636
36 36
363636
( (( 111))) 36
36
1
6
i
36( (11 )36
1
6
i
1)
36
1
6
i
6i
Вычислите:
900
1
4
12,25
5.
iiii1i ; ii2133231321i;ii;2i (( (i 11 )1)ii)i i 2 i 2;i2i2i22;; (3
2
i
1
;
3
2
i
1
;
i
iiii
i
i
i
i
i
i
i
i
i
i
(
(
1
1
i
(
(
1
1
)
)
i
i
;
;
2
2
3
2
i
i
i
i
i
(
1
i
i
i
i
i
(
iiiiii i iii2ii(2ii4i3i3 i 3 i1 ( (() ( i 1 11 1) i))ii)i iii i i i ; i i ;i;i; ;i3 2ii222 2 ( (1( ) 1
iiii ii iii3444(3443iii
1
)
i
;
3
2
i
i
i
i
(
1
2
2
2
i
1
i
i
;
i
i
i
(
1
)
i
i
i
(
1
i
i
1
1
i
i
i
;
;
i
i
i
i
(
(
1
1
3
3
2
2
4
2
iiiiii
i
i
1
i
i
;
i
i
1
i
i
;
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
1
i
i
;
3
3ii44
2
2
4
i
i
i
(
1
)
1
;
2
54i54i
24
i
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
i
i
1
1
i
i
;
i
;
4
3
i
i
1
i
i
;
3
5
5
2
2
2
4
i i i i i ( 1
2
2
4 3
4344343
33244
234344 4
5
545544
5
44355
4
4
5
5
5
36 5
656565
6
5566
456656 6
47767676
66777
67767 7
58777
588
7788
iii 4i4ii 555 iii 11ii iii iii;i;i222 i
i1 11 ;;; ii i
i
i
iii i i i4i4 i5 5ii 5 iii11 iiii i ii;i; 2iii222 11;;
iii i i i i i5665665 i1 i i i i ii
11 i ii i ; i i ii
;; i i2i225 5 14 4;11;;
i
ii(i((
ii111i2 2 );)) i i iii
i i1ii 1;i; ;i;;i 11 i
i666 6 1iii
iiiiii ii i5i5ii5
i
i
(
1
i
i
;
5 i6 6ii
22)
i
i
i
i
i
1
1
;
;
i
(
1
)
i
1 1;;i
;55ii;;
iiii i i i i i76767 6i iii i i ii
i i
(i(ii (
2 1 1i
)i1)2 )i
ii i16 6
;
ii 6i6i777 ii ( ( ii11 )i)i i i1 1 .. . iii; ; ii ii i
6.
Значения степеней числа iповторяются с периодом,
равным 4.
Найдем:
28
33
135
i ;i ;i .
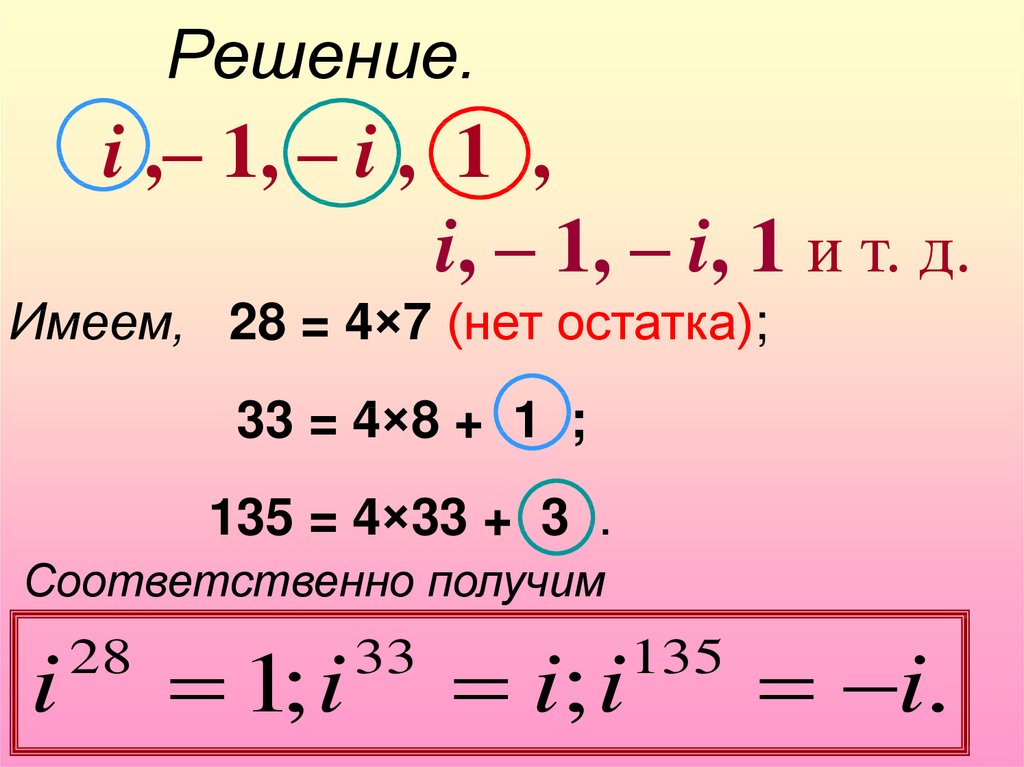
7.
Решение.i ,– 1, – i , 1 ,
i, – 1, – i, 1 и т. д.
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
i
28
1; i
33
i; i
135
i.
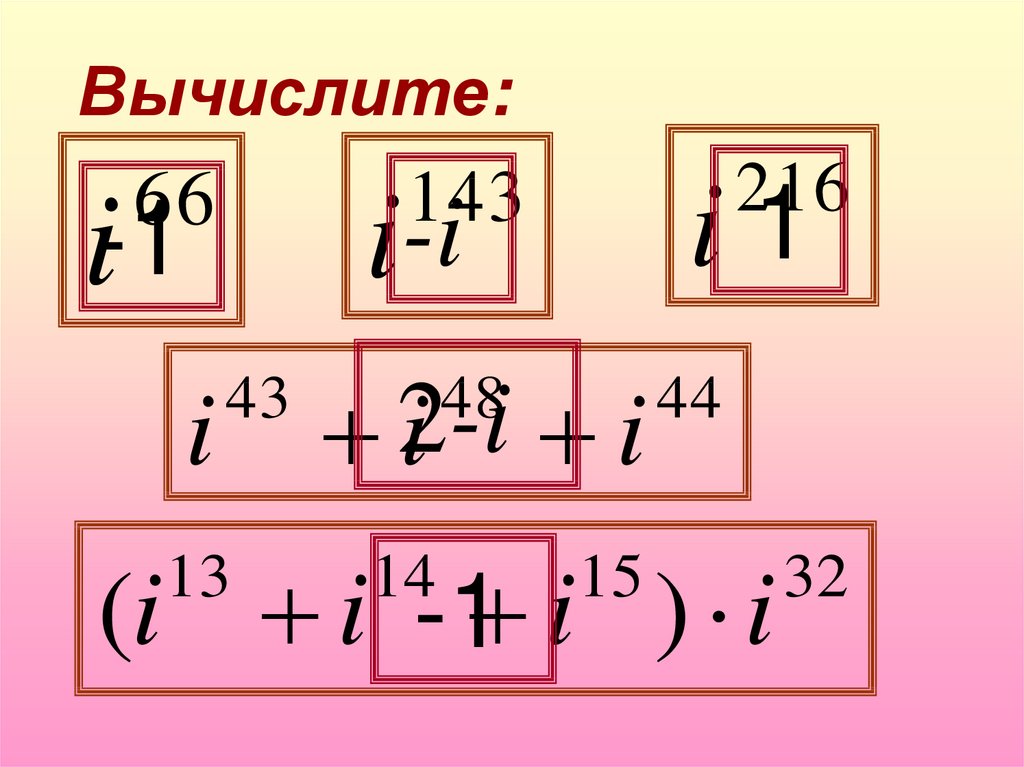
8.
Вычислите:i1
i-i
i-1
i
216
143
66
43
2-i
i i
48
44
(i i -1 i ) i
13
14
15
32
9. Комплексные числа
Определение 1. Числа вида a + bi,где a и b – действительные числа,
i – мнимая единица,
называются
комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
10. a + bi = c + di, если a = c и b = d.
Определение 2.a + bi = c + di, если
a = c и b = d.
11. Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда
Пример .Найти x и y из равенства:
3y + 5xi = 15 – 7i;
Решение.
Согласно условию равенства
комплексных чисел имеем
3y = 15, 5x = – 7.
7
Отсюда x , y 5.
5
12. (а+bi)
Сложение(а+bi)+(c+di)=(a+c) + (b+d)i
Вычитание
(а+bi)- (c+di) =(a-c) + (b-d)i
13. Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
Решение.
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 + 10i;
14. Умножение
(а+bi)(c+di) == ac + аd i + bс i +
2
bd i
= (ac-bd) + (аd+bc)i
=
15. Выполните действия:
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2 = 34
(2 –
2
7i)
2
49i
= 4 - 28i +
=-45-28i
2
2
2
25m +16 = 25m -16i =
= (5m-4i)(5m+4i)
16. Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой
частью.z1= a+bi
и
z2=a-bi
17. Деление
2 3i 2 3i 5 7i=
5 7i 5 7i 5 7i
=
11 29i
74
=
11 29
i
74 74
18.
Выполните действия:(2 3i ) (4 i )
27
4i
1 i
6 2i 1 i
4
8
i
4i =
4
i
=
1 i 1 i
2
=
2
19. Домашняя работа
6317
13
82
72
34
1) (i +i +i +i )(i –i );
2)
Найти x и y из равенства:
(2x + 3y) + (x – y)i = 7 + 6i.
3)
6 2i 2 3i
3
123
(1 i ) i
3 7i 2 5i




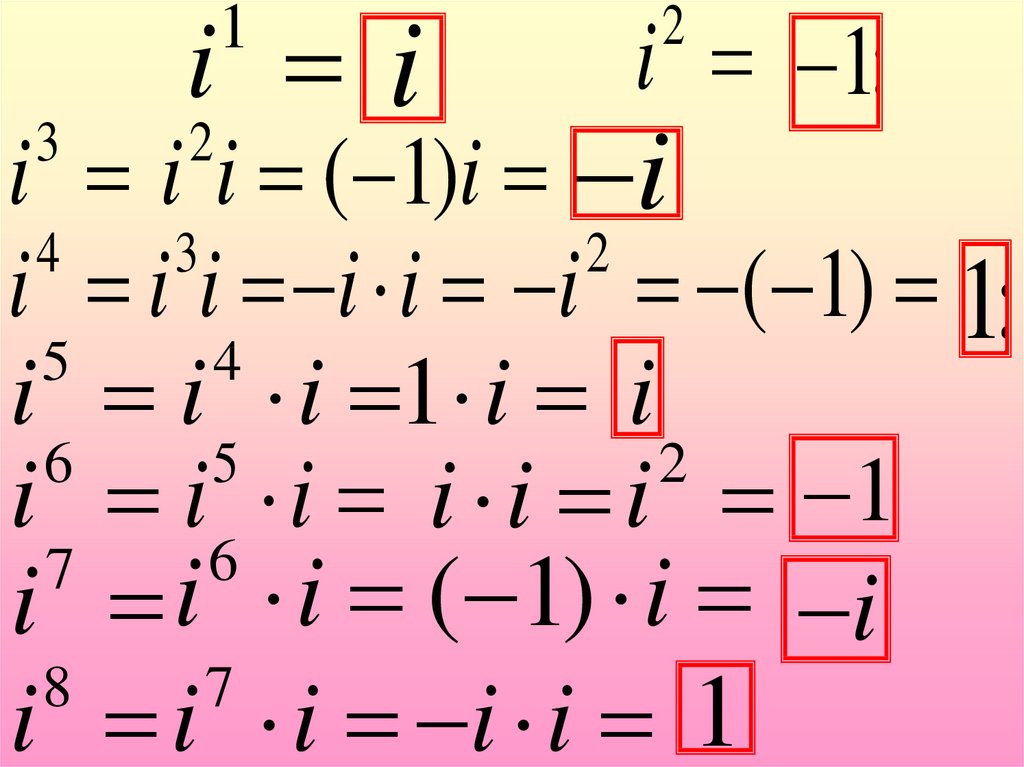




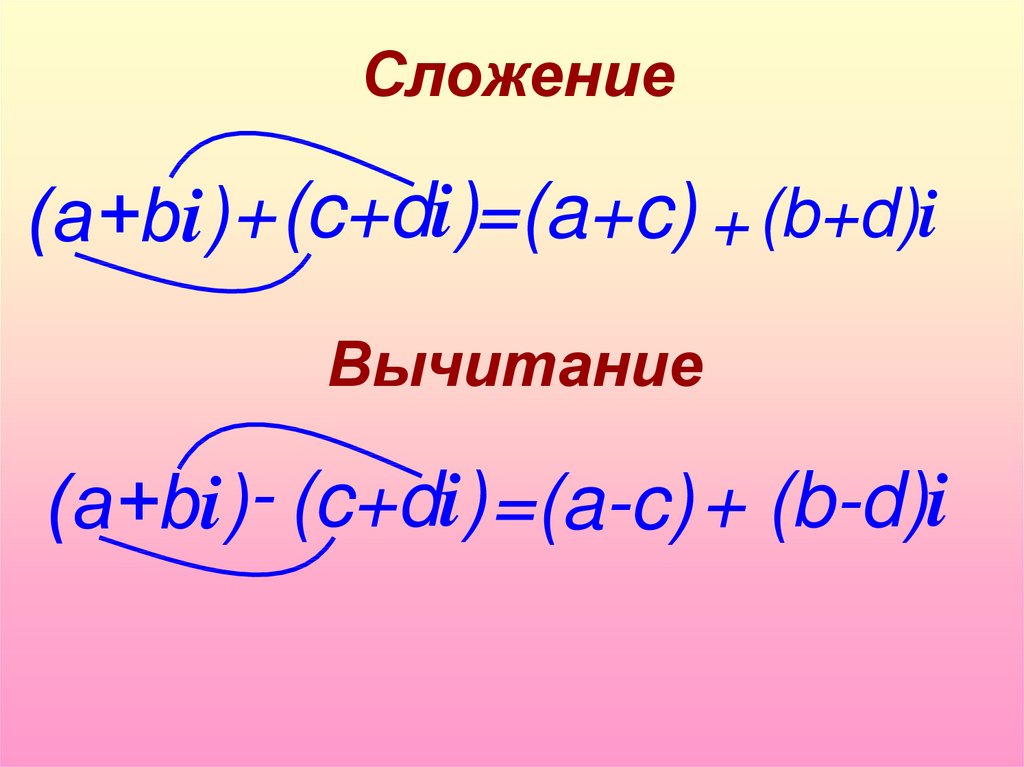

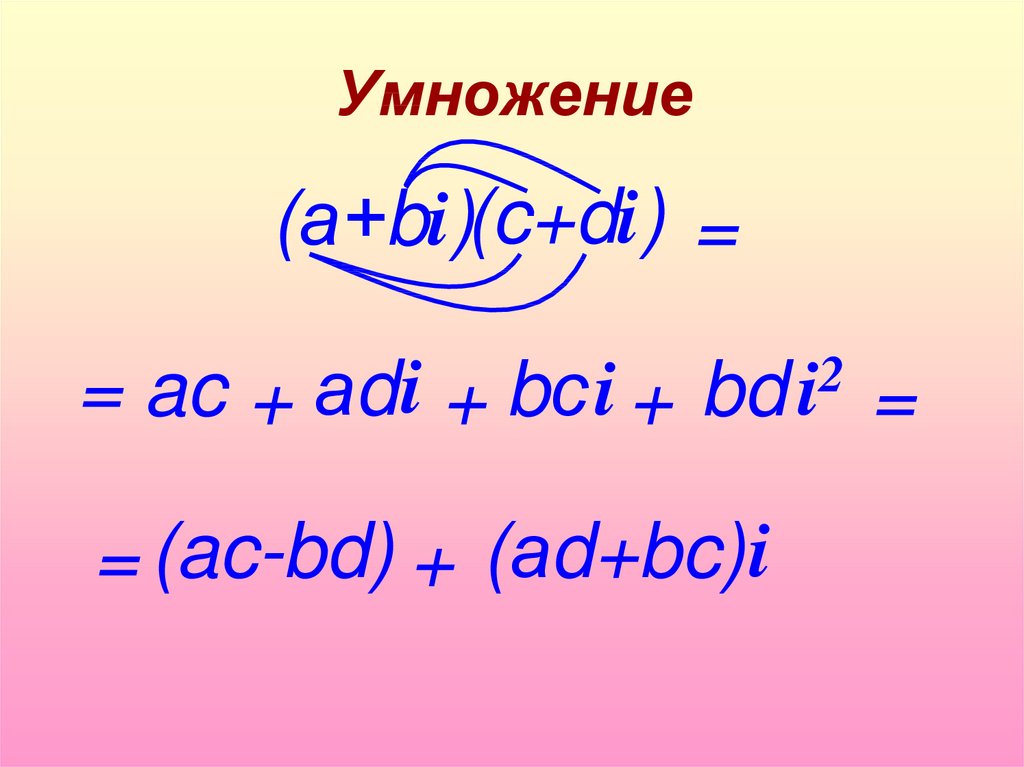





 mathematics
mathematics








