Similar presentations:
Комплексные числа в алгебраической форме
1. Комплексные числа
2. ПЛАН:
1. Основные понятия. Формы записи.2. Действия над комплексными числами:
a) Сложение комплексных чисел;
b) Вычитание комплексных чисел;
c) Умножение комплексных чисел;
d) Деление комплексных чисел ;
3.
Вычислите: 144 126,25 2,5
8 1
64
256 16 2
900
4.
Мнимаяединица
i – начальная буква французского
слова
imaginaire – «мнимый»
5. Например,
3636
36 36
363636
( (( 111))) 36
36
1
6
i
36( (11 )36
1
6
i
1)
36
1
6
i
6i
6.
i;
i
;
1
;
1
;
i
1
;
i
;
i
;
2
2
22
i
;
2
2
i
;
2
2
2
1
2
1
i
1
;
1
;
i
1
;
i
1
;
2
2
2i22
2
i
1
;
i
1
;
i
1
;
i
1
;
2
1
;
3
2
i
i
i
i;3iiii33
1
;
i
1
2
2
1
;
1
;
2
2
2
2
i
1
;
2
i
i
(
1
)
i
i
;
i
1
;
i
1
;
i
1
;
i
1
;
3
2
i
i
(
1
)
i
i
;
i
i
i
(
1
)
i
i
;
33
2
3
2
i
i
(
i
i
;
2
3
2
3
2
2
2
2
3
2
3
3
2
3
2
3
2
i
i
i
(
1
)
i
i
;
3
2
i
i
i
(
1
)
i
i
;
3
2
3
2
3
2
2
i
i
(
1
)
i
i
;
i
(
1
)
i
i
;
1
;
(
1
)
i
;
i
(
1
)
i
i
;
3
2
i
i
i
i
;
i
i
i
(
1
i
i
(
1
1
)
i
i
;
3
2
i
(
1
)
i
i
;
2
3
2
(
1
)
i
i
;
i
(
i
;
ii4iiiiii(i344i
1
)
i
i
i
i
(
)
i
;
i
(
1
)
i
i
;
i
i
1
)
i
i
;
3
2
i
i
(
1
)
i
i
;
3
2
i
i
i
(
1
)
i
i
(
1
)
i
i
;
i
i
i
(
1
)
i
i
;
i
i
i
(
1
)
i
i
;
i
i
(
1
)
i
i
;
3
2
3
2
i
i
i
(
1
)
i
i
;
i
i
i
i
i
(
1
)
4i44
2
3
23
4
3
2
3
2
4
2
4
3
2
i
i
i
i
i
(
1
)
i
i
i
i
i
(
3
2
3
2
i
i
(
1
)
i
i
;
4
3
2
4
3
2
4
3
4
3
2
4
3
2
4
3
2
4
2
4
2
i
i
i
i
i
i
(
1
)
;
i
i
i
i
i
(
1
)
4
3
2
3
2
4
3
2
1
i
i
i
i
i
i
(
1
i
i
i
i
i
(
1
)
1
;
4
3
2
3
2
4
3
2
4
3
2
i
i
i
i
i
(
1
i
i
(
1
)
i
i
i
(
1
)
i
i
i
i
i
(
1
)
1
;
4
3
2
i
i
i
i
i
i
(
1
)
i
i
i
i
i
i
i
i
i
(
1
)
1
;
i
i
(
1
)
1
;
i
(
1
)
1
;
4
3
i
i
i
(
1
)
1
;
i
i
(
1
)
;
i
i
i
(
1
)
1
;
i
i
i
i
i
i
(
1
i
i
i
i
i
(
1
)
i
i
i
(
1
)
1
;
i
i
i
i
i
(
1
)
1
;
54ii55
i
i
i
i
(
1
)
43
i
i
i
i
i
(
2
i
i
i
i
i
4
4i
5
4
i
i
i
i
i
(
1
)
5
4
i
1
i
i
;
5
4
5
4
555
4 4 i
5
4
i
1
i
i
;
i
i
i
1
i
i
;
4
i
i
1
i
i
;
4
5
4
5
4
4
5
4
5
4
5
4
5
4
i
i
i
1
i
i
;
5
4
5
4
5
4
i
i
i
1
i
i
;
5
4
5
4
i
i
1
i
5
4
i
i
i
1
i
i
;
ii5ii
ii
ii
1
i
i
;
i
i
i
;
1
i
i
;
1
i
;
iiii i4iii
i iii ii i
i
1
i
;
1
i
;
1
i
;
1
i
1
i
i
i
i
i
1
i
i
1
i
;
1
i
i
;
1
i
i
i
1
i
;
4
1
i
i
;
i
i
i
1
i
;
1
;
1
i
i
;
52
4
6 65i5
2;
2
5
2
66i66ii6i6666
1
i
i
5
2
5
6
2
i
i
i
i
i
1
;
5
2
i
i
i
i
i
1
;
i
i
i
1
i
i
i
i
i
i
1
;
5
2
5
2
6
5
2
6
5
2
6
5
2
6
5
2
5
2
6
2
5
2
5
2
6
5
i
i
i
i
i
1
;
i
i
i
i
i
1
;
6
5
2
i
i
i
i
1
;
5
2
5
2
6
5
2;i
55
2
i
i
i
i
1
;
5
2
2
i
i
i
i
1
;
ii66iiiiii
i
i
i
i
i
1
;
2
i
i
i
i
1
;
i
i
i
i
1
;
i
i
i
1
;
i
i
i
i
i
1
i
i
1
;
i
i
i
1
;
i
i
i
1
;
i
i
i
i
i
1
;
i
i
1
i
i
i
i
i
1
;
i
i
i
i
i
i
i
1
;
i
i
i
i
i
i
i
1
i
i
i
i
1
;
i
i
i
1
;
7
6
7
6
i
i
i
i
i
1
;
i
i
i
1
;
5
2
i
i
i
(
1
)
i
i
;
i
i
i
(
1
)
i
i
;
7
6
6
5
7
6
6
7
6
7
7
6
7
6
7
6
77
6
i
i
i
i
i
1
;
7
6
7
6
7
6
6
6
7
6
7
6
i
i
(
1
)
i
i
;
7
i
i
i
(
i
i
;
i
i
(
1
)
i
i
;
6 i
i
i
(
1
)
i
i
;
6
7
6i
i
i
(
1
)
i
i
;
6
i
1
)
i
i
i
i
i
6
i
i
(
1
)
i
i
;
i
i
(
1
)
i
i
6
ii77iiiii7i7i
i
i
1
)
i
i
;
i
i
i
i
(
1
)
i
i
;
i
i
(
1
)
i
i
;
(
1
)
i
i
;
(
1
)
i
;
i
(
1
)
i
i
;
i
i
(
1
)
i
8
7
i
(
1
)
i
i
;
8
7
6
i
i
(
1
)
i
;
i
i
1
)
i
i
;
i
i
i
(
i
i
(
1
)
i
i
;
(
1
)
i
;
(
1
)
i
i
;
i
i
i
i
i
1
.
i
i
i
i
i
1
.
i888
(
1
)
i
i
;
7
i
i
(
1
)
i
i
;
8
7
8
7
7
8
7
7
6
8
7
7
7777 ii i7 iii
ii
ii
i i
1
..7 1. 6
88 ii
7i
8i8
8i7
8
7
8
7
8
i
i
1
i
1
.
i
i
i
1
.
i
i
i
i
i
i
1
.
7
i8ii8ii8i
i
i
i
i
1
.
i
(
1
)
i
i
;
8
7
7
7
i
i
1
.
i
i
i
i
i
1
.
7
i
i
i
i
1
.
7
i
i
i
i
1
.
i
i
i
i
1
.
i
i
1
.
i
i
1
.
i
i
1
.
i
i
iii11
i1... i ii (
i
i8i
iii7 iii
i
iii
.. 1
7. Комплéксные числа
Определение 1. Числа вида a + bi,где a и b – действительные числа,
i – мнимая единица,
называются комплéксными.
a − действительная часть комплéксного
числа,
b – мнимая часть комплéксного числа
Например, Z = 6+2i или Z = 1-5i .
1
2
8. Основные понятия.
Два комплексных числаназываются равными тогда и
только тогда, когда равны их
действительные и мнимые
части.
Два комплексных числа,
отличающихся лишь знаком
мнимой части, называются
комплексно- сопряженными.
z1 1 + 1i ;
z 2 2 + 2i
z1 z2 1 2 ; 1 2
z1 1 + 1i
z2 2 2i
9. Примеры.
Пример 1.z1 5 + 3i ;
Пример 2.
z1 5 + 3i ;
z 2 25 / 5 + 15 / 5i
z 2 5 3i
5 25 / 5
3 15 / 5
Вывод : z1 и z 2
комплексно -
Вывод : z1 z 2
сопряженные числа.
10. Решение. Используя условие равенства комплексных чисел имеем 2y = 13, 4x = – 6, тогда
Найти x и y из равенства:2y + 4xi = 13 – 6i;
Решение.
Используя условие равенства
комплексных чисел имеем
2y = 13,
4x = – 6, тогда
x 1,5; y 6,5.
11. Формы записи комплексных чисел.
1.2.
3.
Алгебраическая.
Тригонометрическая.
Показательная.
Любое комплексное число можно записать в любой
форме.
12. Действия над комплексными числами в алгебраической форме
Сложение и вычитание комплексных чисел.z a + i b1
Суммой (разностью) комплексных чисел
1
1
и
называется комплексное число,
z2 a2 + i b2
определяемое равенством:
z1 + z2 a1 + i b1 + a2 + i b2 a1 + a2 + i b1 + b2
z1 z2 a1 + i b1 a2 + i b2 a1 a2 + i b1 b2
13. (а+bi)
Сложение(а+bi) +(c+di) =(a+c) +(b+d)i
Вычитание
(а+bi) −(c+di) =(a−c) +(b−d)i
14.
z1 = 12 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
а) z1 + z2 =(12 + 3i) + (5 – 7i) =
=(12 + 5) + (3i – 7i) = 17 – 4i;
б) z1 – z2 =(12 + 3i) – (5 – 7i) =
=(12 – 5) + (3i + 7i) = – 7 + 10i;
15. Действия над комплексными числами
Умножение комплексных чисел.Умножением комплексных чисел z a + i b и z a
1
1
1
2
2
называется число, получаемое при умножении этих чисел по
правилам алгебры как двучлены.
z1 z2 a1 + i b1 a2 + i b2
a1 a2 + i b1 a2 + i b2 a1 + i 2 b1 b2
z1 z2 a1 a2 b1 b2 + i b1 a2 + b2 a1
+ i b2
16. Умножение
(а+bi)(c+di) == ac + аd i + bс i + bd
= (ac-bd) + (аd+bc) i
−1
2
i
=
17. Выполните действия:
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2 = 34
(2 –
2
7i)
2
49i
= 4 - 28i +
= -45-28i
2
2
2
25m +16 = 25m -16i =
= (5m-4i)(5m+4i)
18. Действия над комплексными числами
Деление комплексных чисел.Чтобы разделить z1 a1 + i b1 на
z2 a2 + i b2
необходимо умножить делимое и делитель на число, сопряженное
делителю:
z1 a1 + i b1
(a1 + i b1 ) (a2 i b2 )
z2 a2 + i b2 (a2 + i b2 ) (a2 i b2 )
(a1a2 + b1b2 ) + i (a2b1 a1b2 ) a1a2 + b1b2
a2 b1 a1b2
+i
2
2
2
2
a2 + b2
a2 + b2
a22 + b22
19. Деление
2 + 3i 2 + 3i 5 + 7i=
5 7i 5 7i 5 + 7i
=
11 + 29i
74
=
11 29
+ i
74 74
20. Домашняя работа
Найти сложение, вычитание, умножение иделение комплексных чисел:
• Z1 = (3 + 5i) , Z2 = (7 – 2i)
• Z1 = (3 – 2i), Z2 = (5 + 3i)
• Z1 = (4 + 2i), Z2 = (– 3 + 2i).
• Z1 = (– 2 + 3i), Z2 = (7 – 2i)
21. Геометрическое изображение комплексных чисел.
Всякое комплексное числоможно изобразить точкой
плоскости xOy такой,
что x - действительная часть,
Y - мнимая
И, наоборот, каждую точку
координатной плоскости
можно рассматривать как
образ комплексного числа.
Z = + i, М( ,
y
M( ; )
O
x
22. Геометрическое изображение комплексных чисел.
yM(x;y)
O
x
Плоскость, на которой
изображается комплексные
числа, называется
комплексной плоскостью.
Ось абсцисс Ox называется
действительной осью.
Ось ординат Oy называется
мнимой осью.
23. Геометрическое изображение комплексных чисел.
yr OM
M(x;y)
φ
O
x
Комплексное число можно задавать с
помощью радиус-вектора r OM
.
Длина вектора называется модулем
этого числа и обозначается
Z или r .
Величина угла между положительным
направлением оси Ox и вектором
называется аргументом rэтого
комплексного числа и обозначается
Arg Z или j.
Аргумент комплексного числа
определяется с точностью до
слагаемого 2pk.




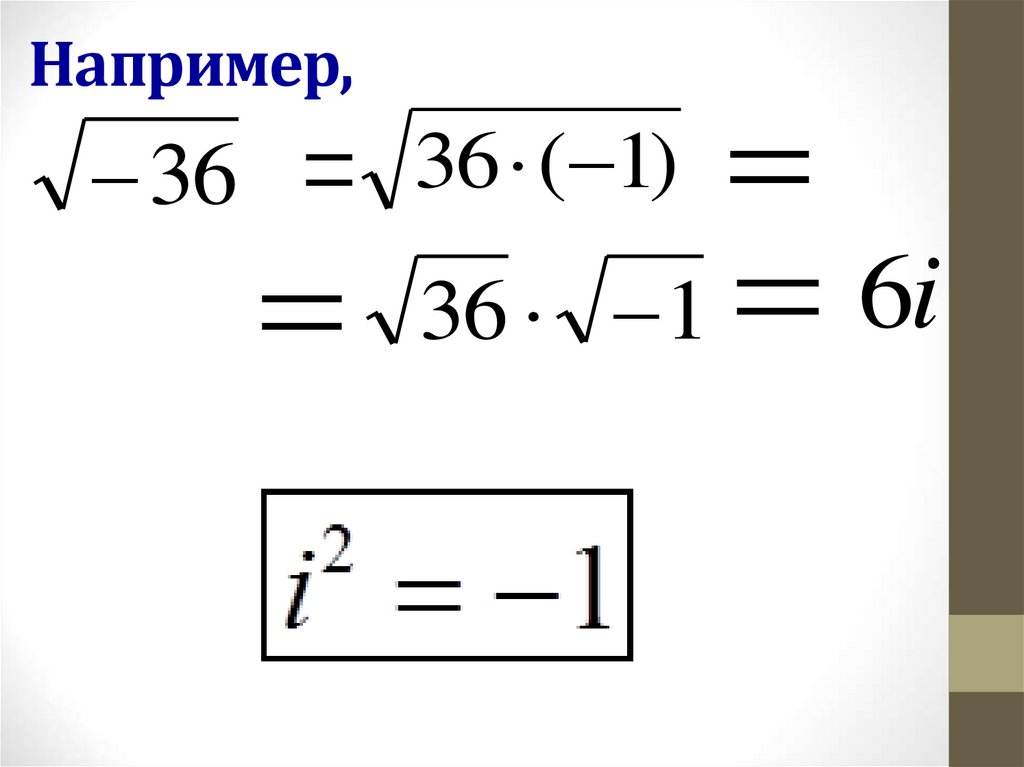
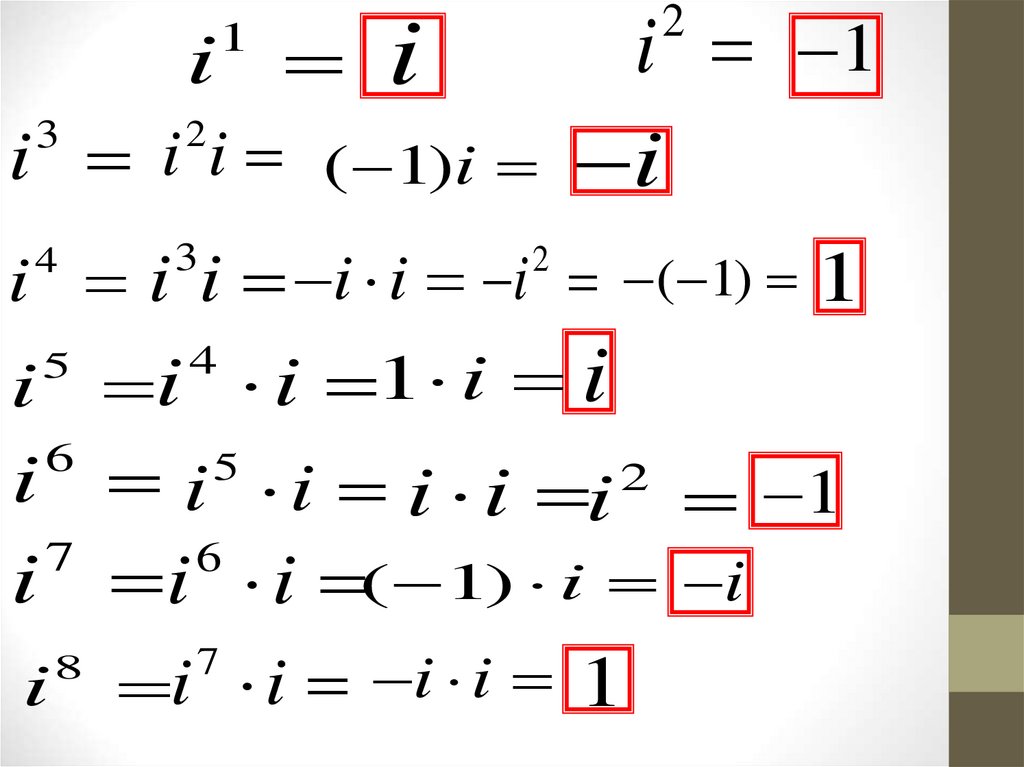







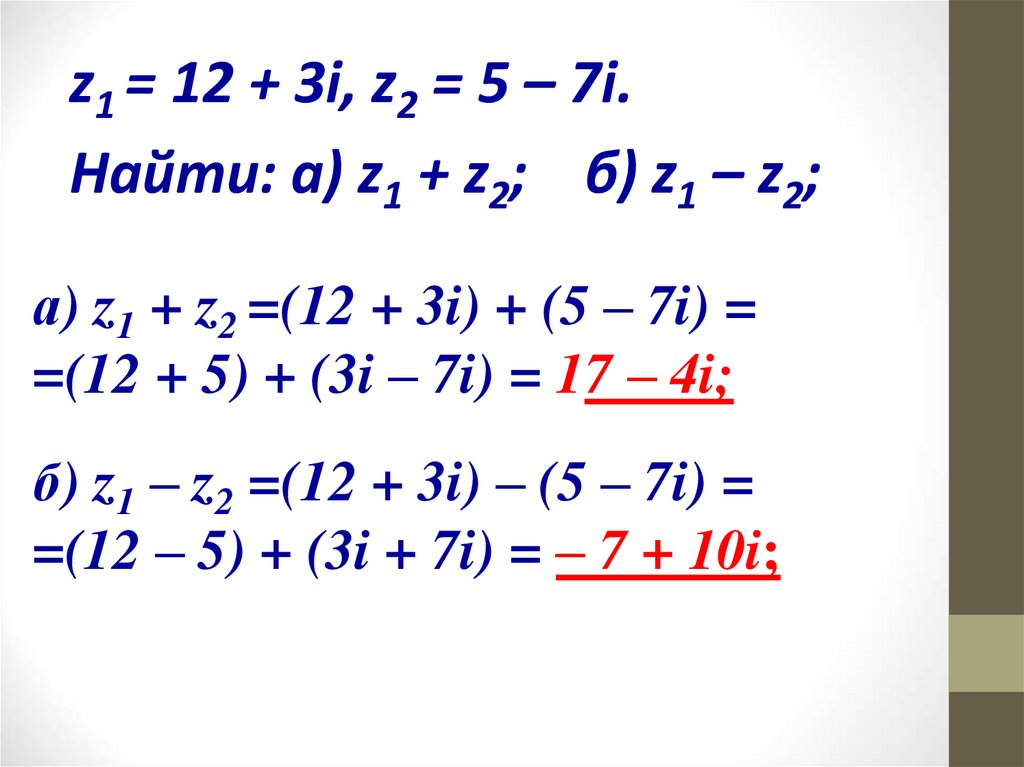

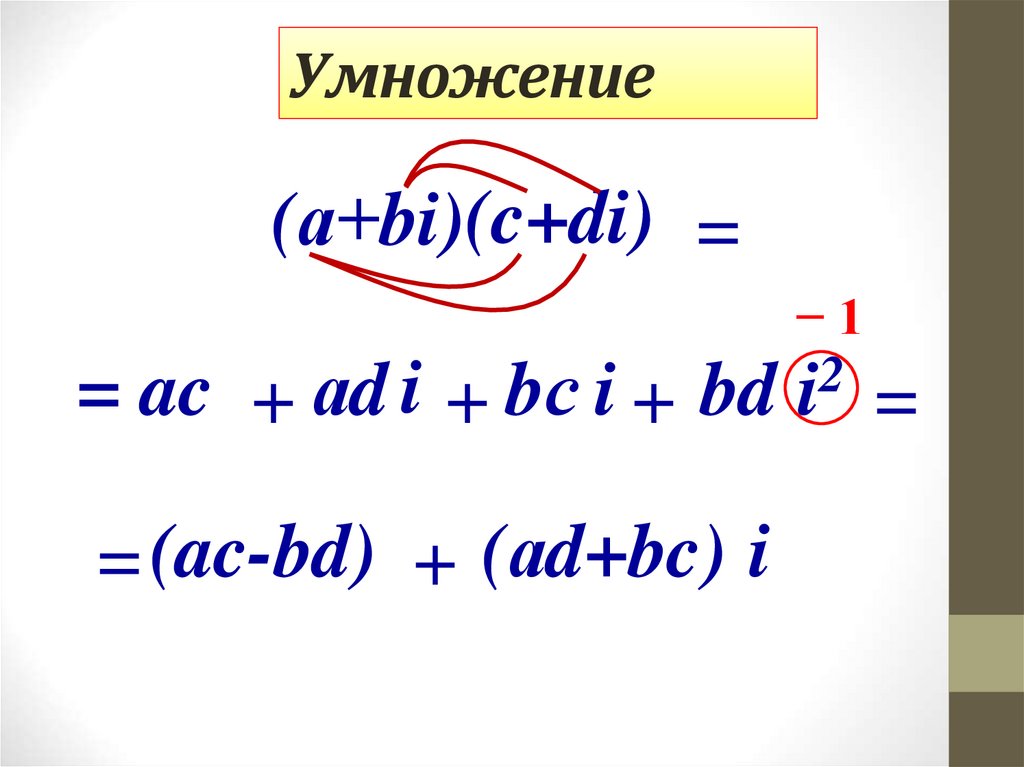







 mathematics
mathematics








