Similar presentations:
Комплексные числа
1. Комплексные числа
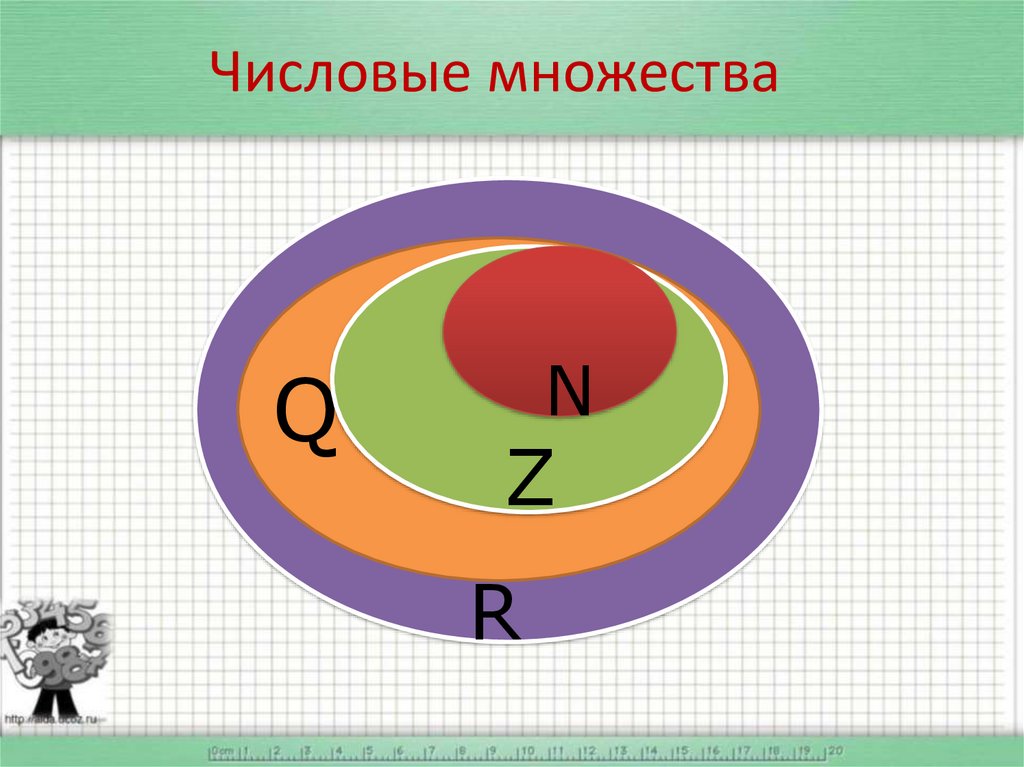
2. Числовые множества
QN
Z
R
3.
i – мнимая единица1 i
i 1
2
4. Пример
1.4 4 1 2i
2.
3.
x 25
x 2 10 x 34 0
x 25
D b 2 4ac 100 136 36
2
x 5i
10 36 10 6i
x1
5 3i
2
2
x2 5 3i
5.
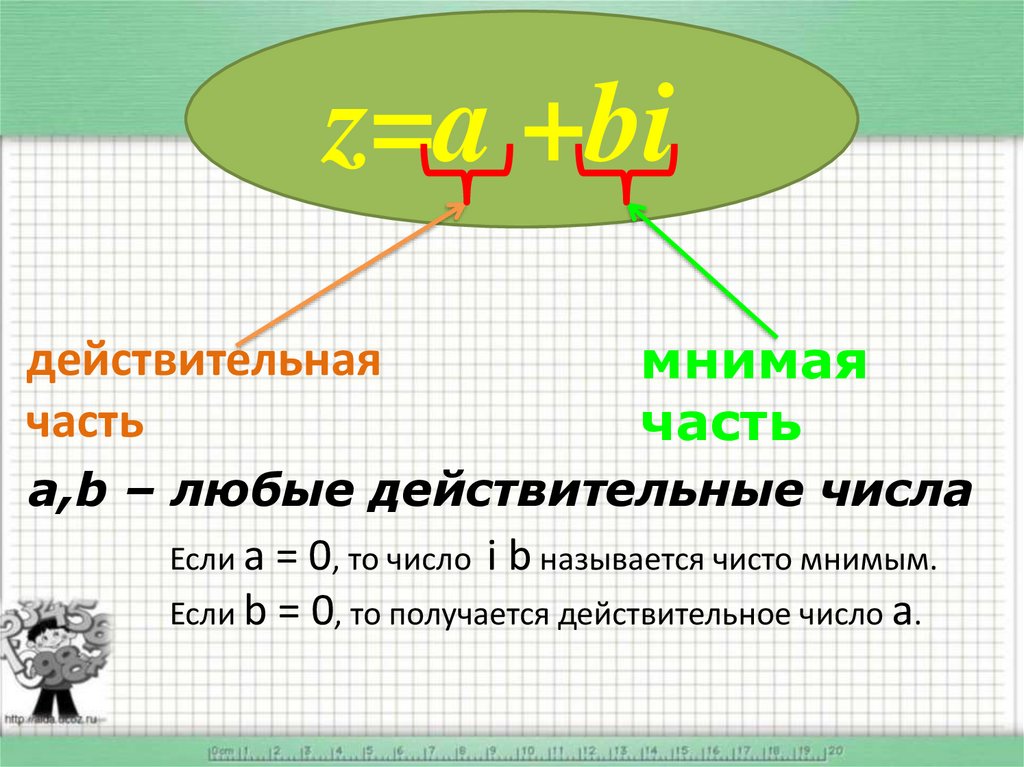
z=a +biдействительная
часть
мнимая
часть
a,b – любые действительные числа
Если а = 0, то число i b называется чисто мнимым.
Если b = 0, то получается действительное число а.
6.
Пример7.
Действия с комплексными числами• Сложение
•Вычитание
•Умножение
•Деление
•Возведение в степень
•Извлечение корня
8. Сложение комплексных чисел
Общая формула:z1 z2 a1 b1i a2 b2i a1 a2 b1 b2 i
Пример 1.
z1 4 6i, z2 5 7i
9.
Сложение комплексных чиселПример 2.
z1 5 4i, z2 7 9i
z1 z2 5 4i 7 9i 5 4i 7 9i 2 5i
Пример 3.
z1 2 3i, z2 1 5i
Ответ: 1 + 8i
10. Вычитание комплексных чисел
Общая формула:z1 z2 a1 b1i a2 b2i a1 a2 b1 b2 i
Пример 1.
z1 4 6i, z2 5 7i
11. Вычитание комплексных чисел
ВЫЧИТАНИЕ КОМПЛЕКСНЫХ ЧИСЕЛПример 2.
z1 5 4i, z2 7 9i
z1 z2 5 4i 7 9i 5 4i 7 9i 12 13i
Пример 3.
Ответ: 3 -2i
z1 2 3i, z2 1 5i
12. Произведение комплексных чисел
Произведением комплексных чисел являетсякомплексное число:
z1 a bi, z 2 c di
z1 z 2 (a bi )(c di )
ac bci adi bdi
2
(ac bd ) (bc ad )i
13. Произведение комплексных чисел
Пример 1.z1 4 6i, z2 5 7i
14. Пример 2
Произведение комплексных чиселz1 5 4i, z2 7 9i
Пример 2
Решение
2
z1 z 2 5 4i 7 9i 35 45i 28i 36i
35 45i 28i 36 1 73i
Пример 3.
z1 2 3i, z2 1 5i
Ответ:
-17 + 7 i
15. Если у комплексного числа сохранить действительную часть и поменять знак у мнимой части, то получится комплексное число,
Сопряженные числаЕсли у комплексного числа сохранить
действительную часть и поменять знак у
мнимой части, то получится
комплексное число, сопряженное
данному, которое обозначается
z a bi
комплексное число;
z a bi
сопряженное число.
16. Деление комплексных чисел
Для того, чтобы разделить два комплексныхчисла, нужно делимое и делитель умножить на
число, сопряженное делителю, т.е.
a bi (a bi )(c di )
c di (c di )( c di )
ac bci adi bdi
2
2
c (di )
(ac bd ) (bc ad )i
2
2
c d
2
17. Деление комплексных чисел
Пример 1.z1 4 6i, z2 5 7i
18. Пример 2
Деление комплексных чиселПример 2
5 4i
5 4i 7 9i 35 45i 28i 36i 2
2
2
7 9i 7 9i 7 9i
7 9i
35 45i 28i 36 71 17i
71 17
i
49 81
130
130 130
Пример 3.
z1 2 3i, z2 1 5i
Ответ:
0,5-0,5i
















 mathematics
mathematics








