Similar presentations:
Развитие понятия о числе комплексные числа продолжение
1. Развитие понятия о числе комплексные числа продолжение
Занятие три2. Степени мнимой единицы
3. В чем ошибка?вопрос из дз
4.
2 ;3 3 2iiii4342431
2
i
i
(
(
1
1
)
)
i
i
i
;
i
;
2
1
1
;
;
2
1
4
3
3
3
2
2
2
2
2
3
2
i
i
i
i
i
(
i
i
i
(
1
)
i
i
;
4
3
2
i
1
;
4
3
2
i
1
;
iiii332 4
i
i
i
i
i
i
i
i
i
i
(
(
1
1
i
(
(
1
1
)
)
i
i
;
;
i
2
2
3
2
i
i
i
i
i
(
1
i
i
i
i
i
(
ii2ii53i4344i 4 i iiii2i(2ii4i3i3 i 3 i1 ( (() ( i 1 11 1) i))ii)i iii i i i ; i i ;i;i; ;i3 2ii222 2 ( (1( ) 1
iiii5545545i4i iii3444(3443iii
1
)
i
;
3
2
i
i
i
i
(
1
2
2
2
i
1
i
i
;
i
i
i
(
1
)
i
i
i
(
1
i
i
1
1
i
i
i
i
;
;
i
i
i
i
i
(
(
1
1
4
4
3
3
2
2
5
4
2
iiii345i545i 5
i
i
1
i
i
;
i
i
1
i
i
;
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
1
i
i
;
3
3
2
2
4
4
4
i
i
i
(
1
)
1
;
3
2
66565i
54i54i
24
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
i
i
i
1
1
i
i
;
i
;
4
3
i
1
i
i
;
3
6
5
5
2
2
2
5
4
iiii5566i6 4i4ii 5
i
i
i
(
1
i
i
i
i
1
;
i
i
i
i
i
2
i
i
i
i
55 ii
22
i
1
1
;
;
1
1
i
i
i
i
;
;
ii45i6656
i4i4 i5 5ii5 iii11 iiii i ii;i; 2iii222 11;;
i
i
6
i4i7i677676i i i i i5665665 i1 i i i i ii
11 i ii i ; i i ii
;; i i2i225 5 41 4;11;;
i6 1ii iii(
ii 1
iii7 i ii
i ;)ii ii i i 1 1i i;i; 11 i
iiii666767
(
(
1
1
i
i
;
;
5i5i 66 ii
22)) ii
i
i
(
1
i
i
;
7
i
(
1
i
i
;
5i5 i6 6ii6
2)
2)
i
i
i
i
i
i
i
1
1
;
;
i
i
(
1
)
i
7
7
7
1 1;;i
;55ii;;
ii5ii875877i i i i i76767 6i iii i i ii
i i (i(ii (
2 1 1i
)i1)2 )i
ii i16 6
;
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
i
i
i
;
;
i
i
i
i
i
i
1
.
8
7
i
i
1
.
.
8
7
i 77 8 i 66 7 i i i 1;
5.
6.
Значения степеней числа iповторяются с периодом,
равным 4.
Найдем:
28
33
135
i ;i ;i .
7.
Решение.i ,– 1, – i , 1 ,
i, – 1, – i, 1 и т. д.
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
i
28
1; i
33
i; i
135
i.
8.
9.
Вычислите:i1
i-i
i-1
i
216
143
66
43
2-i
i i
48
44
(i i -1 i ) i
13
14
15
32
10. Комплексные числа
Определение 1. Числа видаa + bi,
где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
11.
VII в.н.э.-квадратный корень из
положительного числа
имеет два значения –
положительное и
отрицательное,
а из отрицательных
чисел квадратные корни
извлечь нельзя:
нет такого числа х,
чтобы
х2 = -9.
12. В XVI веке
в связи с изучениемкубических уравнений
оказалось необходимым
извлекать квадратные корн
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.
13.
Он предложила а а
Кордано назвал такие величины
“чисто отрицательными” или даже
“софистически отрицательными”,
считая их бесполезными и
стремился не применять их.
14. Название “мнимые числа” ввёл французский математик и философ Р. Декарт
в 1637году
15. один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare (мнимый)
в 1777году
16.
В настоящее времякомплексные числа
используются
в математике
гораздо шире, чем
действительные
17. a + bi = c + di, если a = c и b = d.
Определение 2.18. Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда
Пример .Найти x и y из равенства:
3y + 5xi = 15 – 7i;
7
x , y 5.
5
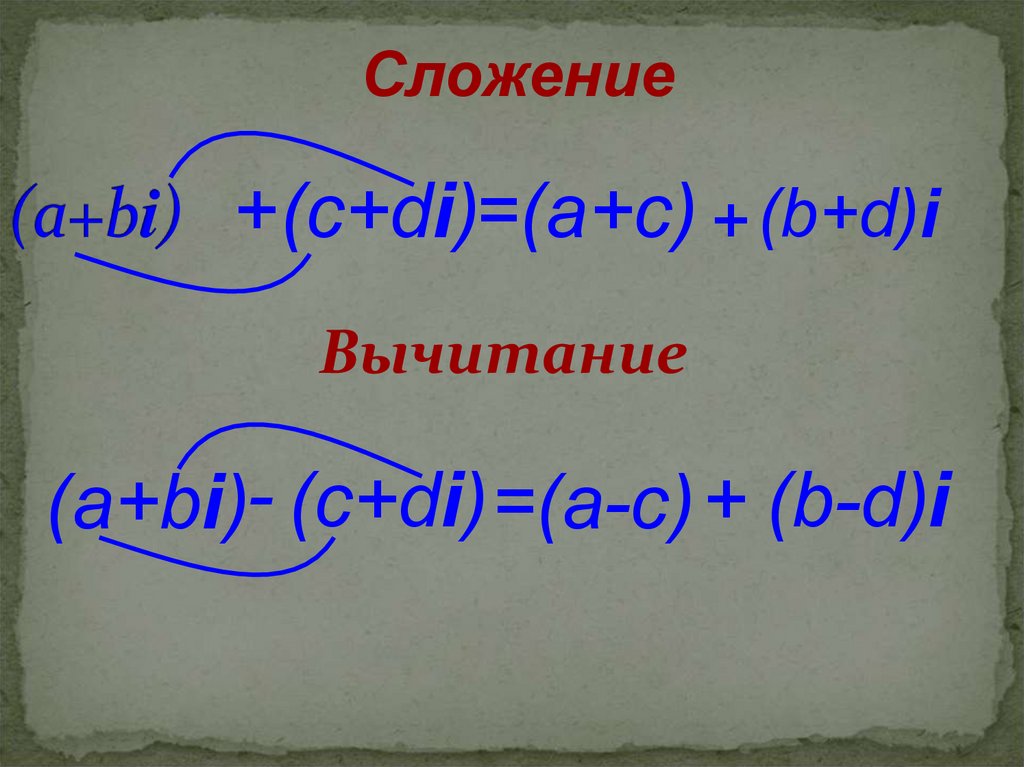
19. (а+bi)
Сложение+(c+di)=(a+c) + (b+d)i
Вычитание
(а+bi)- (c+di) =(a-c) + (b-d)i
20. Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.Найти: а) z1 + z2; б) z1 – z2;
Решение.
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 –
4i;
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 +
10i;
21. Умножение
(а+bi)(c+di) =2
i
= ac + аd + bс i + bd i =
= (ac-bd) + (аd+bc)i
22. Выполните действия:
(2 + 3i)(5 – 7i) == (10+21) + (-14+15)i = 31+i
(5 + 3i)(5 – 3i) = 25-9i2= 34
2
(2 – 7i)
2
= 4 - 28i + 49i
=-45-28i
2
2
2
25m +16 = 25m -16i =
= (5m-4i)(5m+4i)
23. Выполните действия
z1 2 4i _____ z2 3 5i1) z1 z2 _______ 2) z1 z2
3) z1 z2
4) z1
2
24.
25.
26. Деление
2 3i 2 3i 5 7i=
5 7i 5 7i 5 7i
11 29i
11 29
=
=
i
74
74 74
27.
28. Запиши примеры и выполни сам
29.
30. Выполни сам и проверь себя
(2 3i ) (4 i )27
4i
1 i
31.
Выполните действия:(2 3i ) (4 i )
27
4i
1 i
6 2i 1 i
4
8
i
4i =
4
i
=
1 i 1 i
2
=2
32. Домашняя работа
6317
13
82
72
34
1) (i +i +i +i )(i –i );
2) Найти x и y из равенства:
(2x + 3y) + (x – y)i = 7 + 6i.
6
2
i
2
3
i
3
123
3)
(1 i ) i
3 7i 2 5i
33. 4.повторение
Сократите дробь:4x 9
2
6 x x 15
2



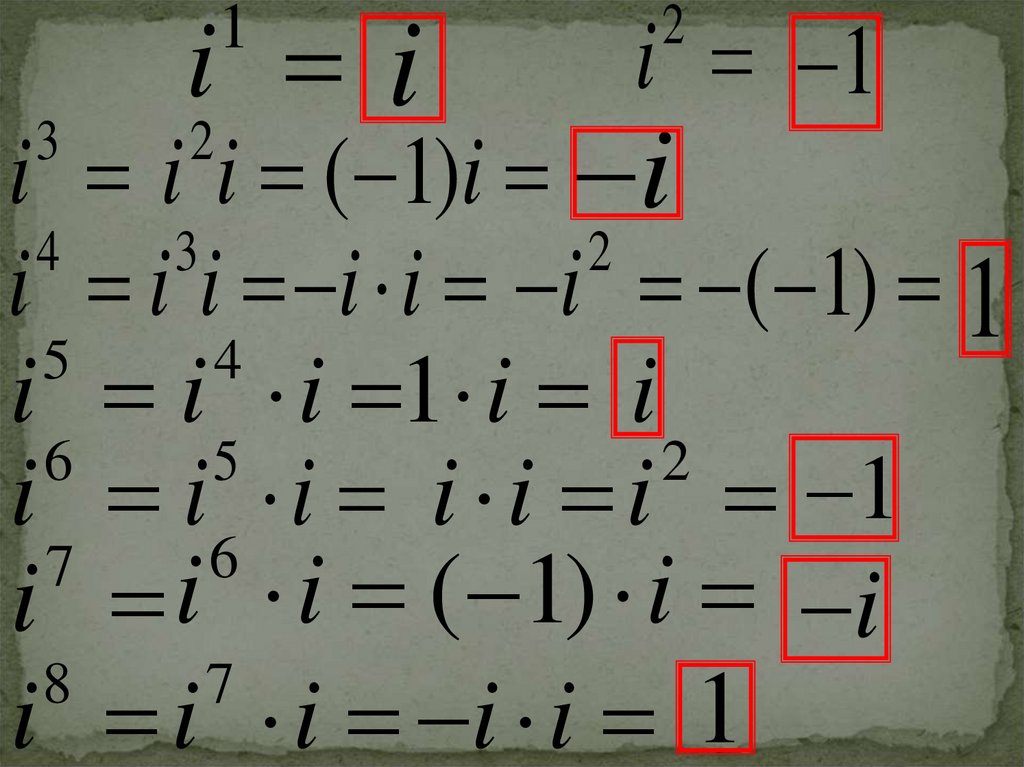












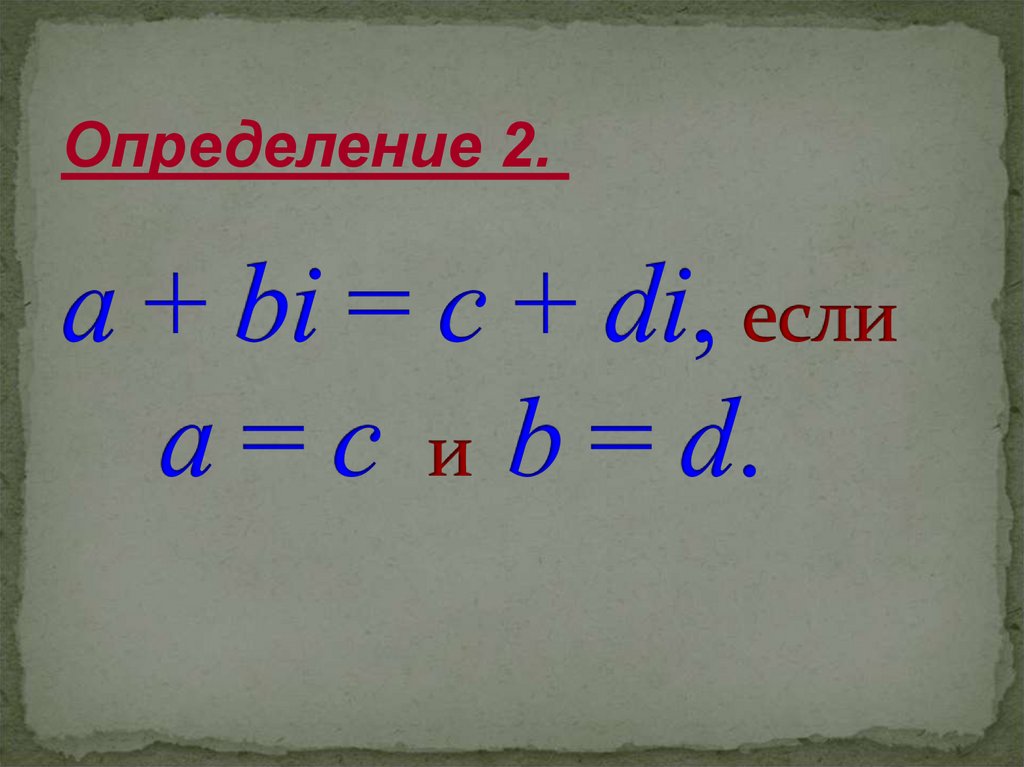


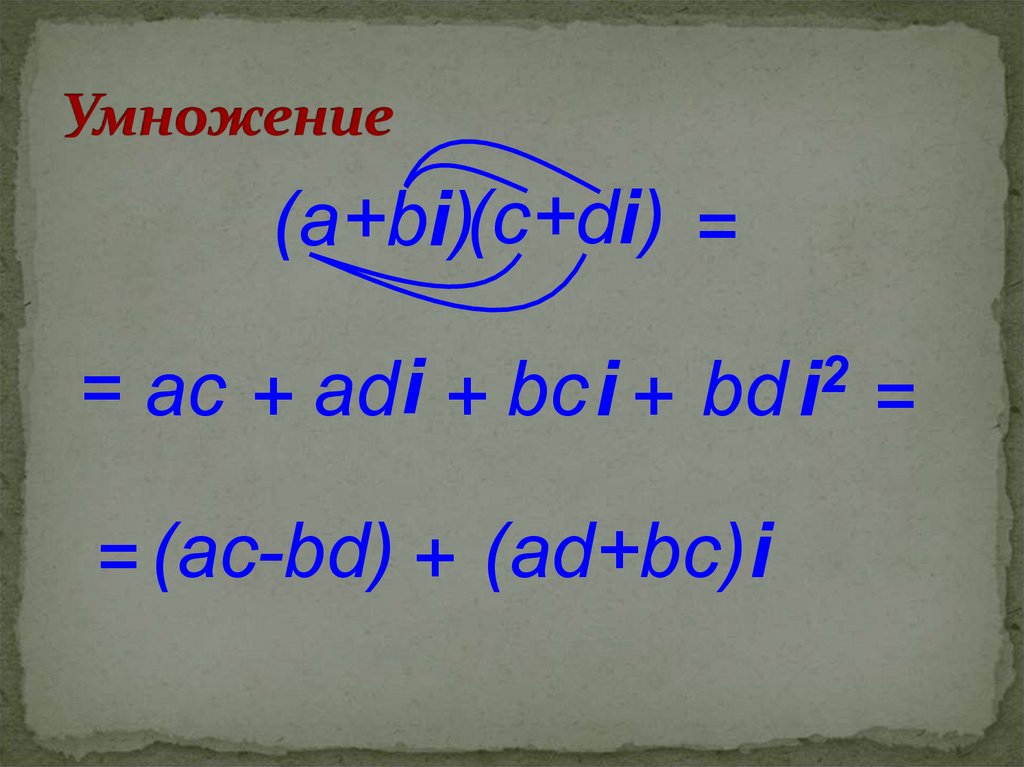




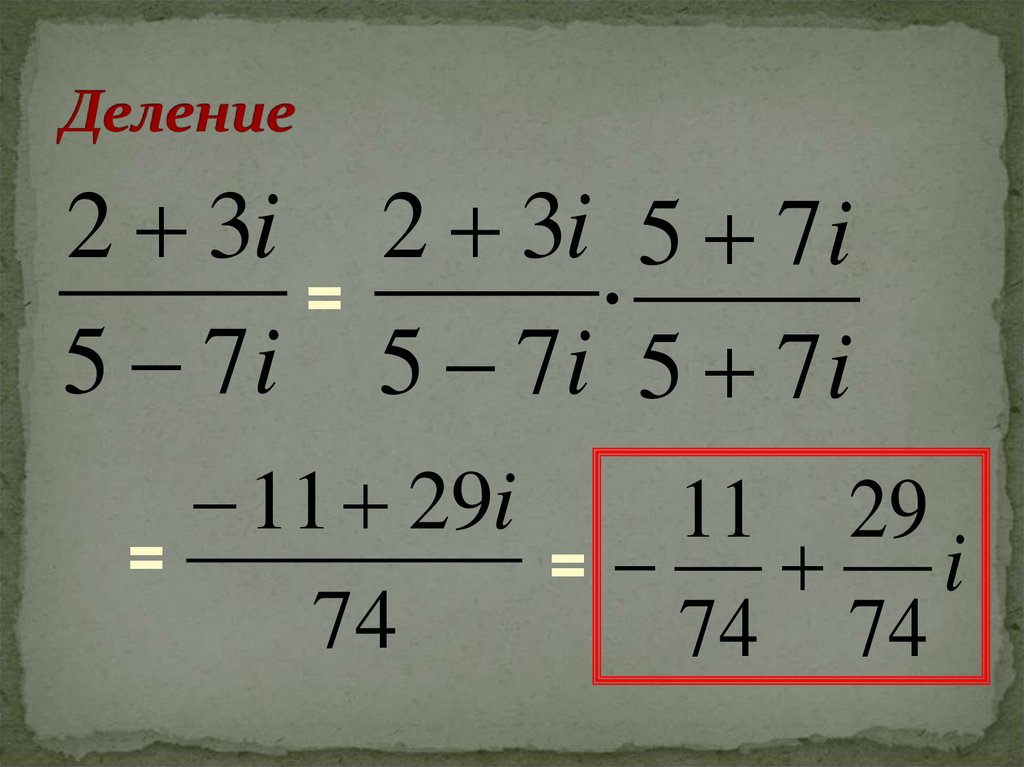







 mathematics
mathematics








