Similar presentations:
Комплексные числа. Действия над комплексными числами
1.
Комплексные числа.Действия над
комплексными
числами.
2
2.
Цели занятия:Образовательные:
• формировать навыки выполнения алгебраических действий над
комплексными числами;
• актуализировать, обобщить и систематизировать знания, умения и
навыки студентов о комплексных числах.
Развивающие:
• развивать мыслительную деятельность студентов на занятии
посредством разнообразия форм заданий;
• способствовать формированию навыков самостоятельной работы и
работы в мини-группах;
• развивать интерес к дисциплине через включение в план занятия
исторического материала и практических заданий.
Воспитательные:
• воспитывать у студентов чувство личной ответственности за
достижение положительных результатов при самостоятельной работе
и в группе.
3
3.
После изучения темы «Комплексные числаучащиеся должны:
Знать:
алгебраическую, геометрическую и тригонометрическую формы
комплексного числа.
Уметь:
•производить над комплексными числами операции сложения,
умножения, вычитания, деления, возведения в степень, извлечение
корня из комплексного числа;
•переводить комплексные числа из алгебраической формы в
геометрическую и тригонометрическую;
•пользоваться геометрической интерпретацией комплексных чисел;
•в простейших случаях находить комплексные корни уравнений с
действительными коэффициентами.
4
4.
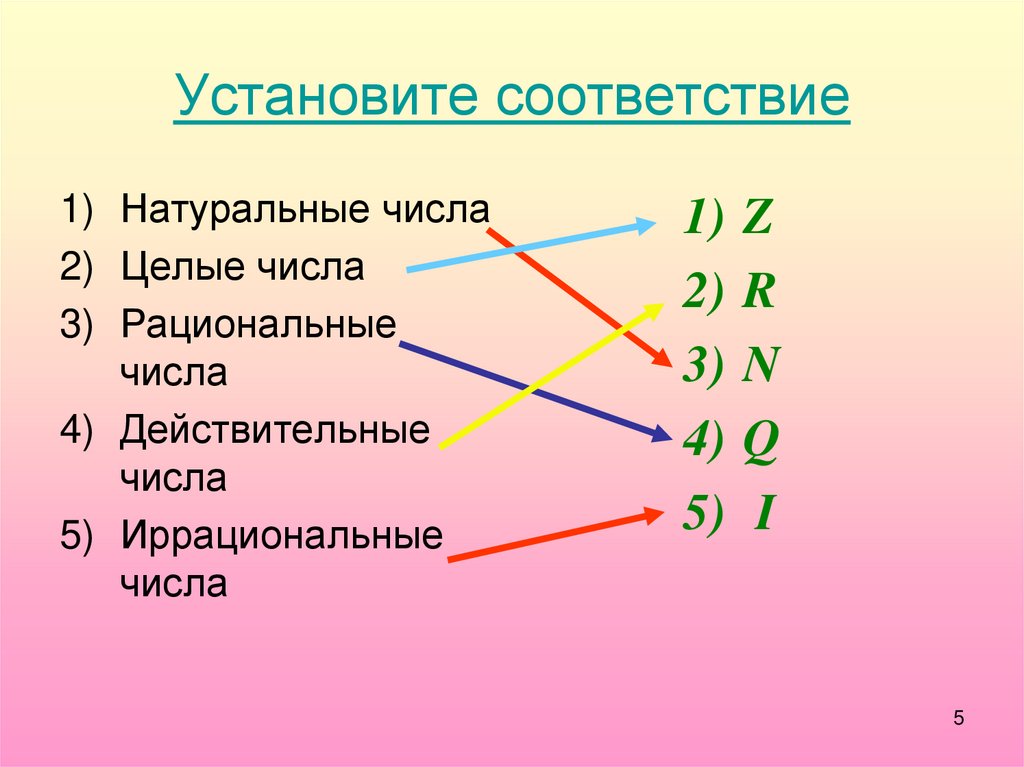
Установите соответствие1) Натуральные числа
2) Целые числа
3) Рациональные
числа
4) Действительные
числа
5) Иррациональные
числа
1)
2)
3)
4)
5)
Z
R
N
Q
I
5
5.
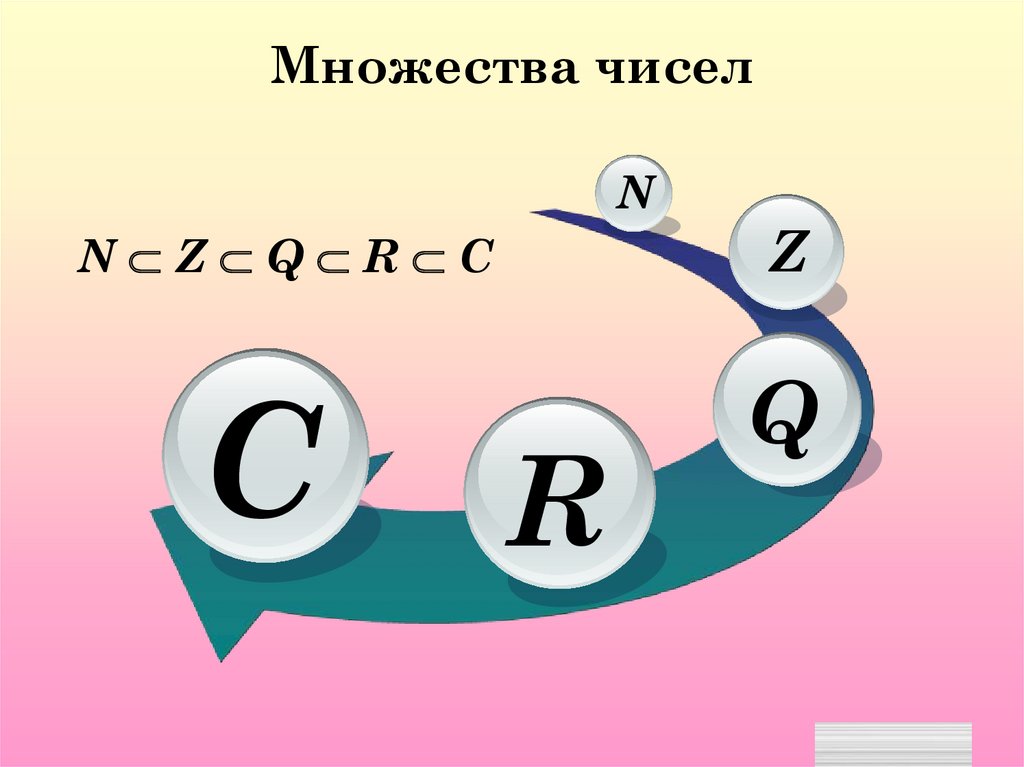
Множества чиселN
N Z Q R C
С
R
Z
Q
6.
Назовите лишнее число в каждойстроке. Ответ обоснуйте
1) 1,2(3); 2,455…; 3,1415…; 7,282828…
2) 45; 34; -111; 3,7; 280; -18
3)
1 4 3 9
; ; ;
3 9 7 16
7
7.
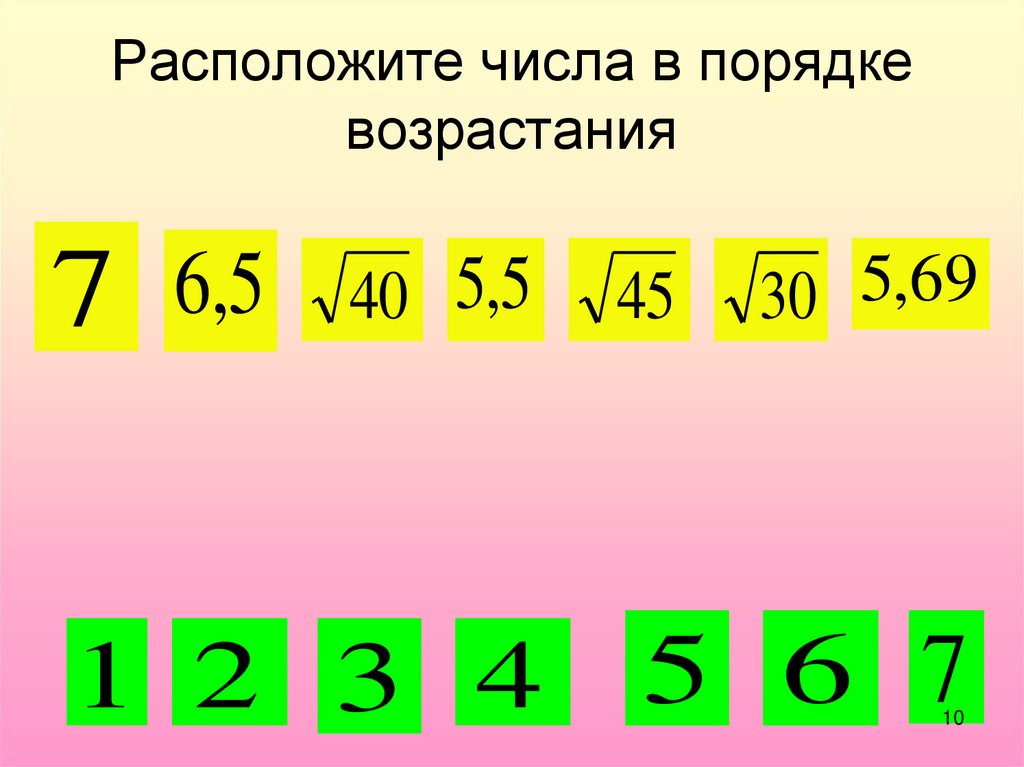
Расположите числа в порядкевозрастания
7
6,5
40 5,5
1 2 3 4
45
5
,
69
30
5 6 7
10
8.
Верно ли решены примеры?1.
2.
3.
4.
5.
6.
7.
8.
-8+(-3)=11
48:(-6)=-8
-3·(-7)=-21
3+(-7)=4
-6-10=-16
17+(-21)=-2
-9·3=27
-6:(-3)=-2
1.
2.
3.
4.
5.
6.
7.
8.
-8+(-3)=-11
верно
-3·(-7)=21
3+(-7)=-4
верно
17+(-21)=-4
-9·3=-27
-6:(-3)=2
13
9.
Содержание:16
10.
1. Мнимаяединица
17
11.
Допустим, что существует такое число, квадраткоторого равен (– 1).
Обозначим это число буквой i.
Тогда можно записать: i2 = - 1.
Число i – называется мнимой единицей.
Из равенства i2 = - 1 находим i 1 . Введение
мнимой единицы позволяет нам теперь извлекать
квадратные корни из отрицательных чисел.
Например:
36 36( 1) 36 1 6i
18
12.
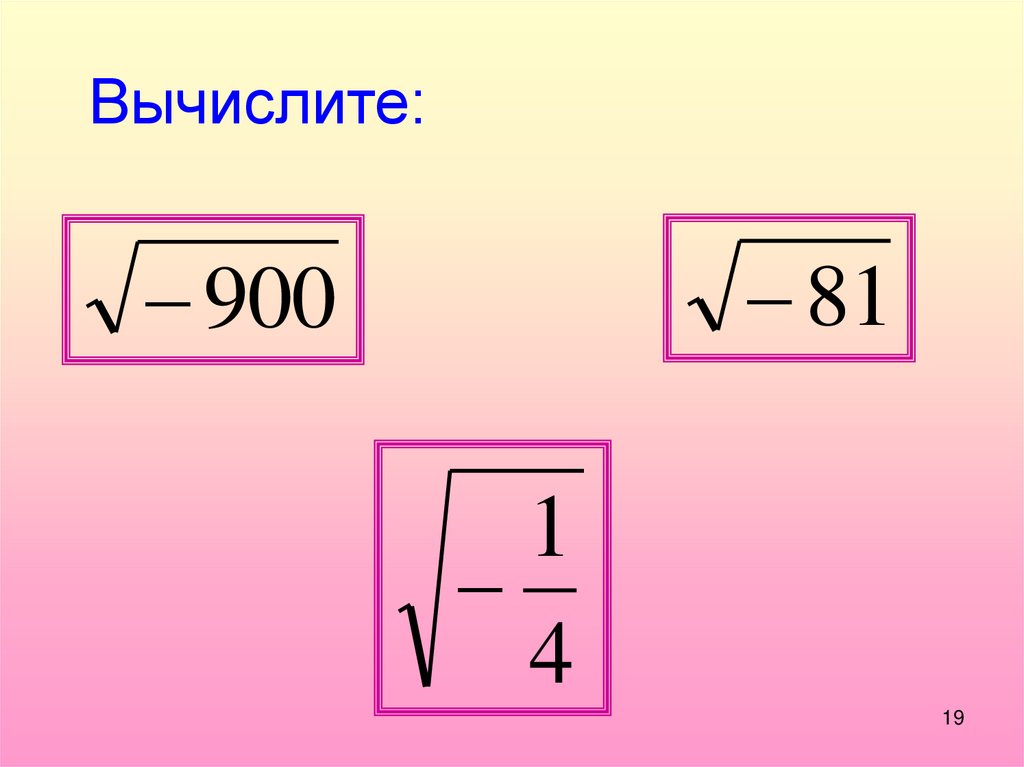
Вычислите:81
900
1
4
19
13.
Пример. Решите уравнение:x2 – 6x + 13 = 0
Решение. Найдем дискриминант по формуле
D = b2 – 4ac.
Так как a = 1, b = – 6, c = 13, то
D = (– 6)2 – 4×1×13 = 36 – 52 = – 16;
Корни уравнения находим по формулам
D 16 16 ( 1) 16 1 4i
6 4i
x1
2
6 4i
x2
2
20
14.
Решите уравнение:1.9 x 12 x 29 0
2
2.x 4 x 13 0
2
3.x 3 x 4 0
2
21
15.
в 1637году
Название
“мнимые числа”
ввёл французский
математик и философ
Р. Декарт
22
16.
Степени мнимой единицы23
17.
iiii1i ; ii2133231321i;ii;2i (( (i 11 )1)ii)i i 2 i 2;i2i2i22;; (3
2
i
1
;
3
2
i
1
;
i
iiii
i
i
i
i
i
i
i
i
i
i
(
(
1
1
i
(
(
1
1
)
)
i
i
;
;
2
2
3
2
i
i
i
i
i
(
1
i
i
i
i
i
(
iiiiii i iii2ii(2ii43ii3 i 3 i1 ( (() ( i 1 11 1) i))ii)i iii i i i ; i i ;i;i; ;i3 2ii222 2 ( (1( ) 1
iiii ii iii3444(3443iii
1
)
i
;
3
2
i
i
i
i
(
1
2
2
2
i
1
i
i
;
i
i
i
(
1
)
i
i
i
(
1
i
i
1
1
i
i
i
;
;
i
i
i
i
i
(
(
1
1
3
3
2
2
4
2
iiiiii
i
i
1
i
i
;
i
i
1
i
i
;
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
1
i
i
;
3
3ii44
2
2
4
i
i
i
(
1
)
1
;
2
54i54i
24
i
i
i
i
i
i
i
i
i
i
i
(
(
1
1
)
)
1
1
;
;
i
i
i
i
1
1
i
i
;
i
;
4
3
i
i
1
i
i
;
3
5
5
2
2
2
4
iiii i 4i4ii 5
i
i
i
(
1
i
i
i
i
1
;
i
i
i
i
i
2
i
i
i
i
55 ii
22
1
1
i
i
i
i
;
;
i
1
1
;
;
iii i i i4i4 5i 5ii5 iii11 iiii i ii;i; 2iii22 11;;
iii i
i i i5665665 i1 i i i i ii
11 i ii i ; i i ii
;; i i2i225 5 41 4;11;;
i
i6 1ii iii(
ii 1
iii i ii
i ;)ii ii i i 1 1i i;i; 11 i
2
2
4 3
4344343
4
2
33 4
234344 4
5
545544
5
44355
4
4
5
5
5
36 5
656565
6
5566
456656 6
47767676
66777
67767 7
58777
588
7788
iiii
(
(
1
1
i
i
;
;
5i5i 66 ii
22)) ii
i
i
(
1
i
i
;
i
(
1
i
i
;
5i5 i6 6ii6
2)
2)
i
i
i
i
i
i
i
1
1
;
;
i
i
(
1
)
i
1 1;;i
;55ii;;
iiii i i i i i76767 6i iii i i ii
i i (i(ii (
2 1 1i
)i1)2 )i
ii i16 6
;
ii 6i6i777 ii ( ( ii11 )i)i i i1 1 . .. iiii; ; ii ii i
24
18.
Значения степеней повторяются спериодом, равным 4.
1. Если показатель степени делится на 4 без
остатка, то значение равно 1.
2. Если показатель степени делится на 4 с
остатком 1, то значение равно i.
3. Если показатель степени делится на 4 с
остатком 2, то значение равно -1.
4. Если показатель степени делится на 4 с
остатком 3, то значение равно -i.
Найдем:
28
33
135
i ;i ;i .
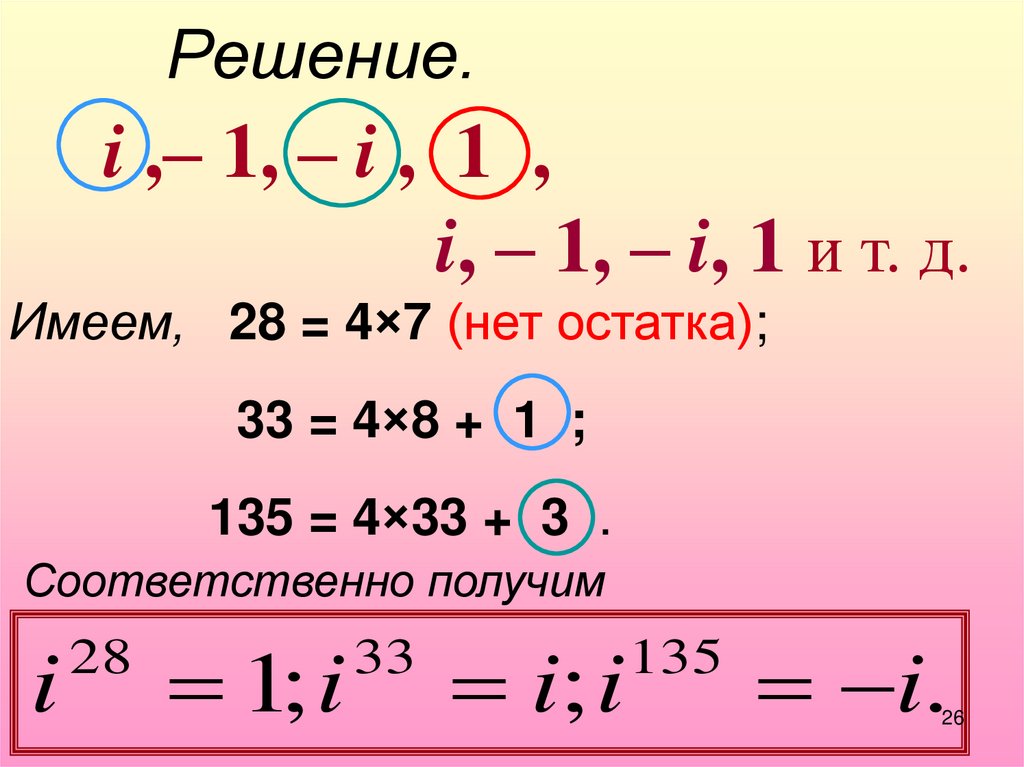
25
19.
Решение.i ,– 1, – i , 1 ,
i, – 1, – i, 1 и т. д.
Имеем, 28 = 4×7 (нет остатка);
33 = 4×8 + 1 ;
135 = 4×33 + 3 .
Соответственно получим
i
28
1; i
33
i; i
135
i.
26
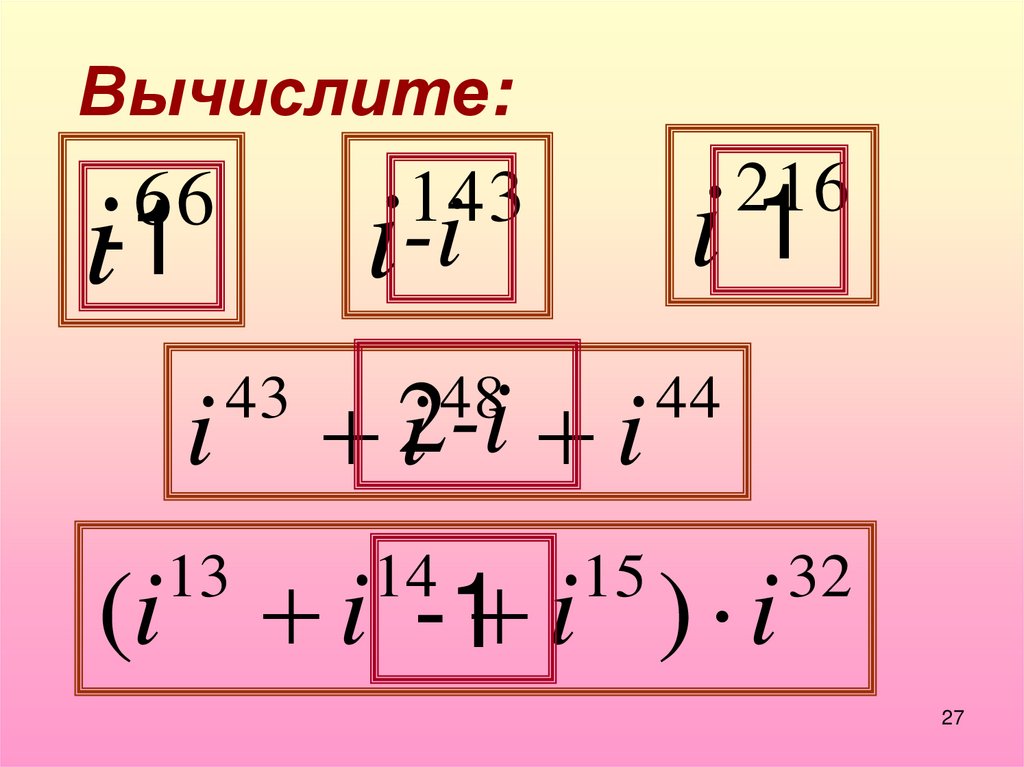
20.
Вычислите:i1
i-i
i-1
i
216
143
66
43
2-i
i i
48
44
(i i -1 i ) i
13
14
15
32
27
21.
Комплексные числаОпределение 1. Числа вида a + bi,
где a и b – действительные числа,
i – мнимая единица,
называются комплексными.
a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.
Обозначение -
z
28
22.
Свойство:Два комплексных числа называются равными,
если равны их действительные части и
коэффициенты при мнимой единице.
a + bi = c + di, если
a = c и b = d.
29
23.
Найти x и y из равенства:3y + 5хi = 15 – 7i
Решение:
3y = 15 ; 5х = - 7
y=5 ;
х = - 7/5
Решите уравнение:
а) 7x + 5i = 1 – 10iy
б) 5х + 3iy = 25 – 12i
в) 7х – 2i = 9 + 5iy
х = 1/7 y = -1/2
х=5
y = -4
х = 9/7
y = - 2/5
30
24.
Действия над комплекснымичислами.
31
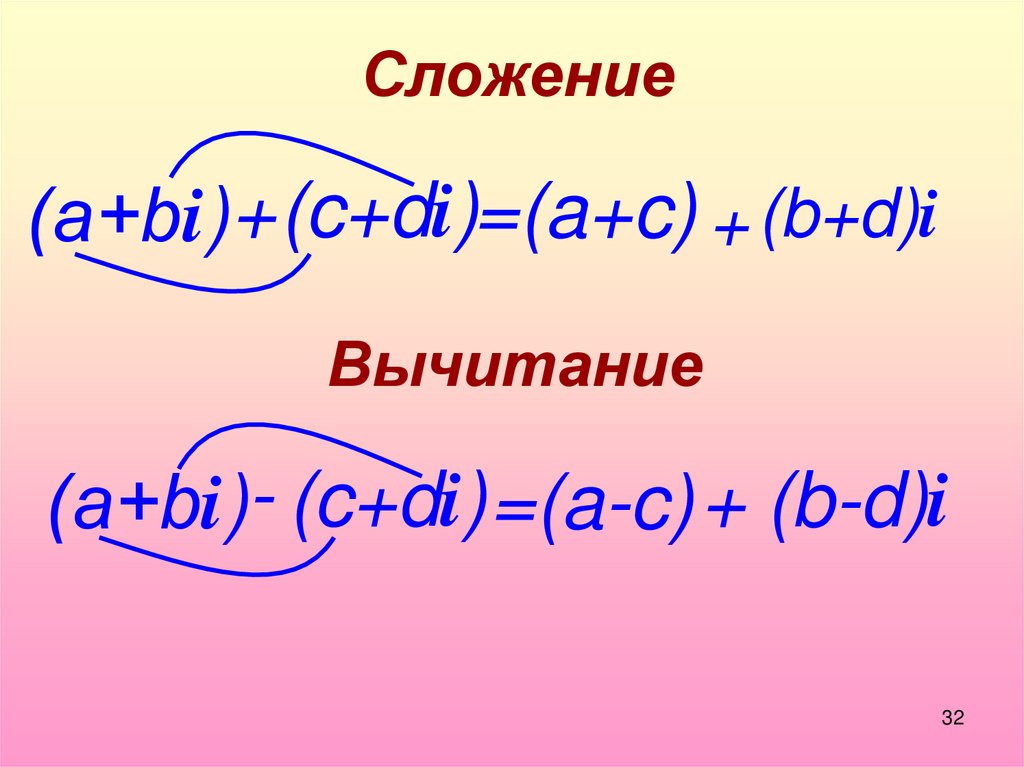
25.
Сложение(а+bi)+(c+di)=(a+c) + (b+d)i
Вычитание
(а+bi)- (c+di) =(a-c) + (b-d)i
32
26.
Выполните действия:z1 = 2 + 3i, z2 = 5 – 7i.
Найти: а) z1 + z2; б) z1 – z2;
Решение.
а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 + 10i;
33
27.
Выполните действие1. (2 + 3i) + (5 + i) = (2 + 5) + (3i + 1i) = 7 + 4i;
2. (– 2 + 3i) – (1 – 8i) = (– 2 – 1) + (3i + 8i) =
– 3 +11i;
3. (– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3i – 3i) =
– 1 + 0i = – 1.
34
28.
Умножение(а+bi)(c+di) =
= ac + аd i + bс i +
2
bd i
Учитывая
i2 =-1
35
29.
Выполните действия:(2 + 3i)(5 – 7i) =
2
= (10-14i + 15i-21i ) = 10+i+21 =
= 31+i
Учитывая
i2 =-1
(5 + 3i)(5 – 3i)=
(2 –
2
7i)
=
36
30.
Два комплексных числа называютсясопряженными, если они
отличаются друг от друга только
знаками перед мнимой частью.
z1= a+bi
и
z2=a-bi
Например:
z1= 2+3i
и
z2=2-3i
37
31.
Деление комплексных чисел.• Чтобы выполнить деление, необходимо
умножить делимое и делитель на число
сопряжённое делителю.
38
32.
Деление2 3i (2 3i) (5 7i)
=
5 7i (5 7i) (5 7i)
=
11 29i
74
=
11 29
i
74 74
39
33.
В настоящее времякомплексные числа
используются
в математике
гораздо
шире, чем
действительные
45
34.
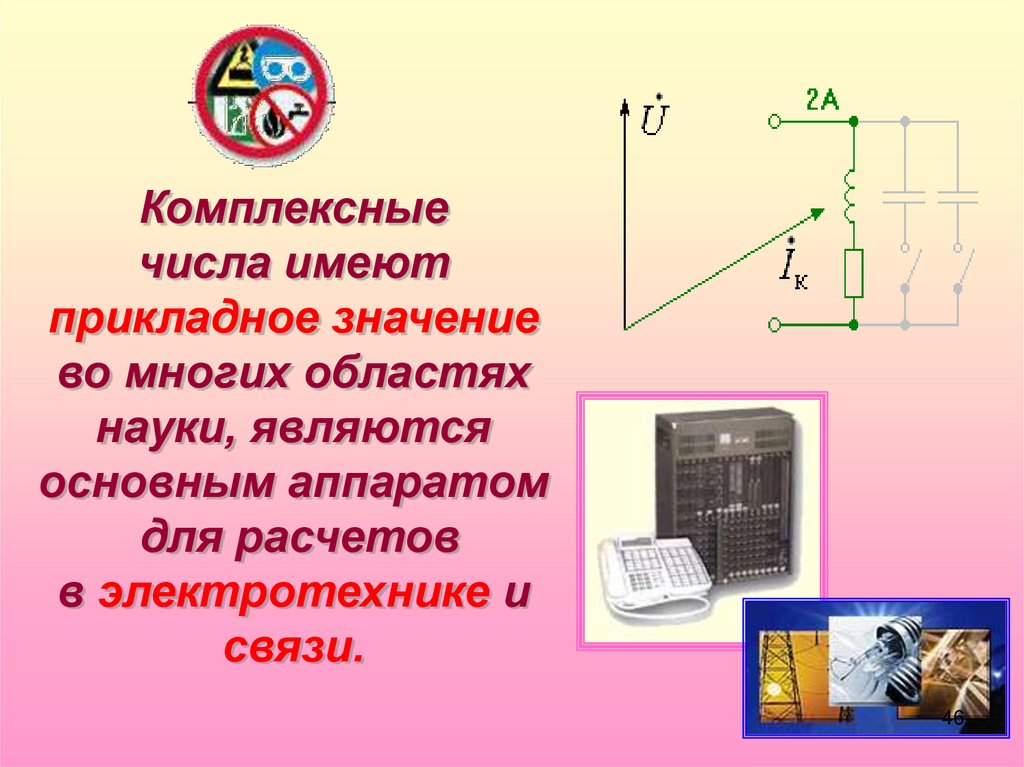
Комплексныечисла имеют
прикладное значение
во многих областях
науки, являются
основным аппаратом
для расчетов
в электротехнике и
связи.
46
35.
Применяютсяпри
конструировании
ракет и
самолетов
47
36.
Привычерчивании
географических
карт
48
37.
В исследованиитечения воды,
а также
во многих
других науках.
49
38.
Пример .Найти x и y из равенства:
3y + 5xi = 15 – 7i;
Решение.
Согласно условию равенства
комплексных чисел имеем
3y = 15, 5x = – 7.
7
Отсюда x , y 5.
5
50
39.
Выполните действия:1).(3 2i ) (7 i )
2.(2 3i)
3.(2 5i )( 2 5i )
2
3 5i
4.
2 6i
51
40.
Выполните действия:3 2i
5.
1 5i
6.(2 7i)
2
7.(1 3i )(1 3i )
52
41.
Выполните действия:(2 3i ) (4 i )
27
4i
1 i
6 2i 1 i
4
8
i
4i =
4
i
=
1 i 1 i
2
=
2
53
42.
Домашняя работа63
17
13
82
72
34
1) (i +i +i +i )(i –i );
2)
Найти x и y из равенства:
(2x + 3y) + (x – y)i = 7 + 6i.
3)
6 2i 2 3i
3
123
(1 i ) i
3 7i 2 5i
55












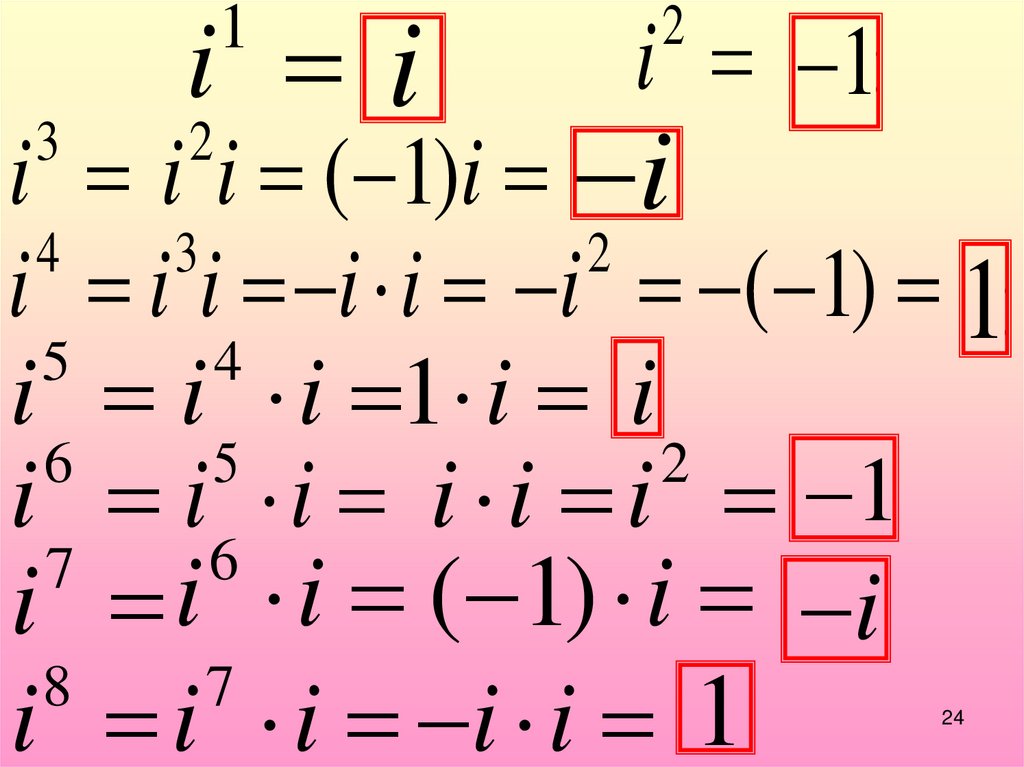




















 mathematics
mathematics








