Similar presentations:
Дискретное преобразование Фурье. Вычисление сверток с помощью ДПФ
1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Дискретное преобразованиеФурье. Вычисление сверток
с помощью ДПФ
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)
2. ЛИНЕЙНАЯ И КРУГОВАЯ СВЕРТКА
Линейная свертка (апериодическая свертка)y ( n)
L 1
m 0
h( n m) x ( m)
L 1
h( m) x ( n m)
m 0
x(n) входная последовательность
h(n) импульсная характеристика системы
Круговая свертка (периодическая свертка)
x ( n)
N 1
m 0
x1 (m) x2 [( n m) mod N ]
x1 (n) первая последовательность
x2 (n) вторая последовательность
N 1
m 0
x1[( n m) mod N ] x2 ( m)
2
3. КРУГОВАЯ СВЕРТКА (1)
3Круговая свертка (периодическая свертка)
x ( n)
N 1
m 0
x1 (m) x2 [( n m) mod N ]
N 1
m 0
x1[( n m) mod N ] x2 ( m)
x1 (n) первая последовательность
x2 (n) вторая последовательность
1) Рассчитывается N-точечное ДПФ каждой из сворачиваемых
последовательностей;
2) Вычисляется произведение N-точечных ДПФ первой и второй
последовательностей
X (k ) X1 (k ) X 2 (k ), k 0, 1, ... , N 1
4. КРУГОВАЯ СВЕРТКА (2). ЛИНЕЙНАЯ СВЕРТКА
4КРУГОВАЯ СВЕРТКА (2). ЛИНЕЙНАЯ СВЕРТКА
ДПФ рассчитывается на основе алгоритмов БПФ.
3)
Вычисляется
обратное
ДПФ
от
результата
вычисления
произведения.
Линейная свертка
1) Линейная свертка лежит в основе цифровой фильтрации;
2) Для перехода от линейной свертки к круговой свертке
последовательности дополняют нулями до длины L;
3) N1 – длина первой последовательности; N2 – длина второй
последовательности; L = N1 + N2 – 1 (требуемое количество нулей для
дополнения первой и второй последовательностей при вычислении
линейной свертки на основе круговой свертки).
5. КРУГОВАЯ СВЕРТКА (3). ЛИНЕЙНАЯ СВЕРТКА
5КРУГОВАЯ СВЕРТКА (3). ЛИНЕЙНАЯ СВЕРТКА
1) y (n)
N 1
x(m)h[(n m) mod N ]
m 0
N 1
h[(n m) mod N ] x( m)
m 0
h(n) импульсная характеристика дискретного или
цифрового фильтра
x(n) входной сигнал (входная последовательность)
2) Y (k ) H (k ) X (k )
Y (k ) ДПФ реакции
H (k ) ДПФ импульсной характеристики фильтра
(после дополнения нулями)
X (k ) ДПФ входного сигнала
(после дополнения нулями)
6. ВЫЧИСЛЕНИЕ СЕКЦИОНИРОВАННЫХ СВЕРТОК (1)
61) При большой длине воздействия вычисление сверток происходит
методом перекрытия с накоплением (если длина воздействия
достаточно большая);
2) Используется представление последовательности в виде коротких
смежных секций длиной L, сравнимой с длиной импульсной
характеристики N1;
3) Линейная свертка формируется на основе коротких
секционированных сверток, вычисляемых с помощью ДПФ и ОДПФ;
4) В MATLAB применяется специальный формат функции fftfilt с
заданием длины секции: y = fftfilt(h,x,L); h – вектор отсчетов
импульсной характеристики; x – вектор отсчетов входного сигнала;
L – длина смежных секций;
7. ВЫЧИСЛЕНИЕ СЕКЦИОНИРОВАННЫХ СВЕРТОК (2). ВЫЧИСЛЕНИЕ ЛИНЕЙНОЙ СВЕРТКИ
75) Операция секционирования позволяет ускорить вычисления
свертки,
если
длина
одной
последовательности
значительно
превосходит длину другой, т.е. N2>> N1.
Вычисление линейной свертки
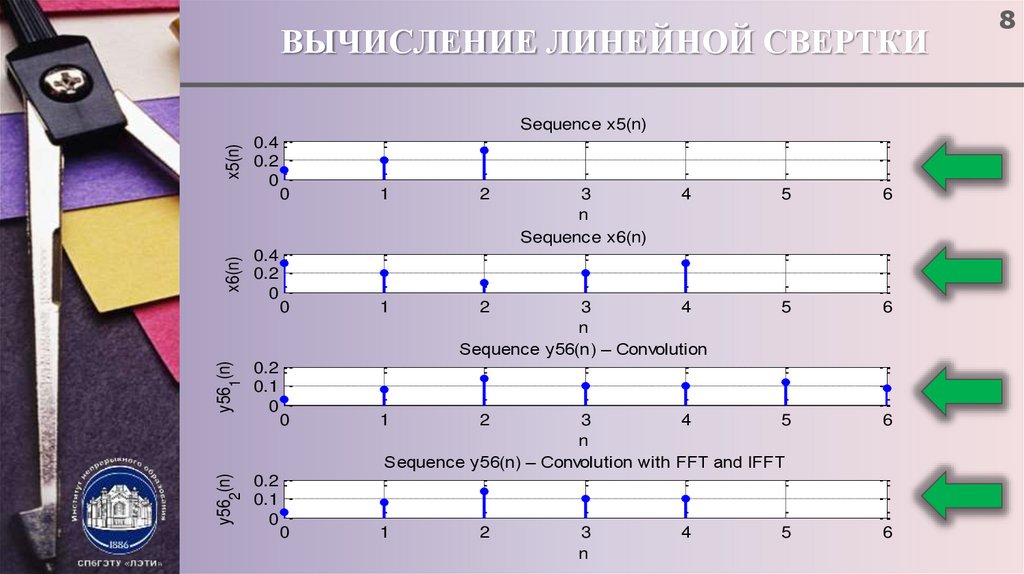
1) x1 = [0.1 0.2 0.3] – 3-элементная последовательность;
2) x2 = [0.3 0.2 0.1 0.2 0.3] – 5-элементная последовательность;
3) Нет ограничений на длины сворачиваемых последовательностей;
4) Длины последовательностей должны быть равны при
вычислении круговой свертки.
8. ВЫЧИСЛЕНИЕ ЛИНЕЙНОЙ СВЕРТКИ
2y56 (n)
1
y56 (n)
x6(n)
x5(n)
Sequence x5(n)
0.4
0.2
0
0.4
0.2
0
0.2
0.1
0
0.2
0.1
0
0
1
2
0
1
2
0
1
2
0
2
3
n
Sequence x6(n)
4
5
6
5
6
3
4
5
n
Sequence y56(n) – Convolution with FFT and IFFT
6
1
6
3
4
n
Sequence y56(n) – Convolution
3
n
4
5
8
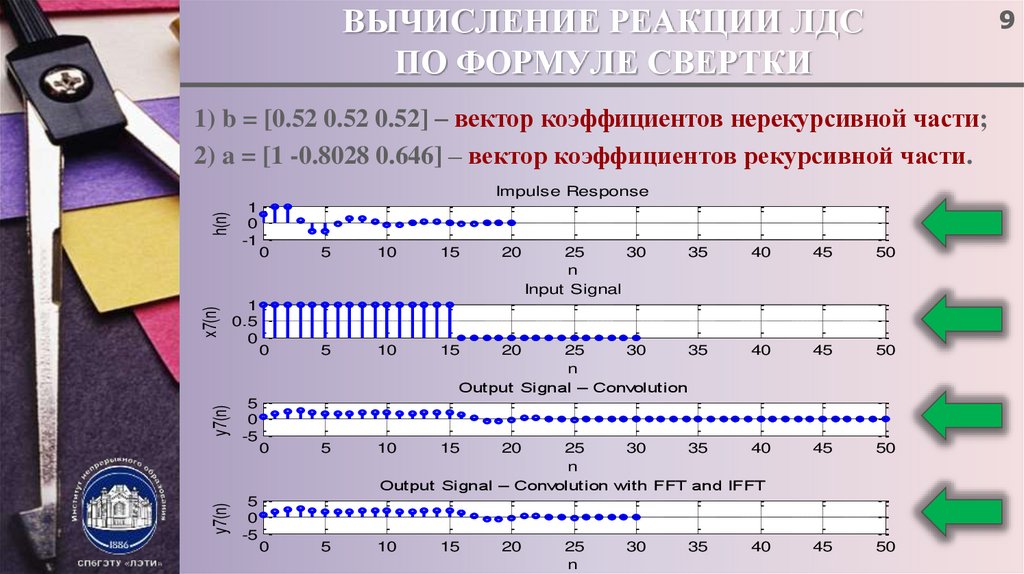
9. ВЫЧИСЛЕНИЕ РЕАКЦИИ ЛДС ПО ФОРМУЛЕ СВЕРТКИ
91) b = [0.52 0.52 0.52] – вектор коэффициентов нерекурсивной части;
2) a = [1 -0.8028 0.646] – вектор коэффициентов рекурсивной части.
y7(n)
y7(n)
x7(n)
h(n)
Impulse Response
1
0
-1
1
0.5
0
5
0
-5
5
0
-5
0
5
10
15
20
0
5
10
15
20
0
5
10
15
20
0
5
15
20
25
30
n
Input Signal
35
40
45
50
25
30
35
n
Output Signal – Convolution
40
45
50
25
30
35
40
n
Output Signal – Convolution with FFT and IFFT
45
50
10
45
50
25
n
30
35
40
10. ВЫЧИСЛЕНИЕ РЕАКЦИИ ЛДС МЕТОДОМ ПЕРЕКРЫТИЯ С НАКОПЛЕНИЕМ
10ВЫЧИСЛЕНИЕ РЕАКЦИИ ЛДС
МЕТОДОМ ПЕРЕКРЫТИЯ С НАКОПЛЕНИЕМ
y8(n)
y8(n)
x8(n)
h(n)
Impulse Response
1
0
-1
1
0.5
0
5
0
-5
5
0
-5
0
20
40
60
80
0
20
40
60
80
0
20
40
60
80
0
20
40
60
80
100
120
n
Input Signal
160
180
200
100
120
140
160
n
Output Signal – Convolution with FFT and IFFT
180
200
100
120
140
160
180
n
Output Signal – Convolution with Overlap-add method
200
100
n
120
140
140
160
180
200
11. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Дискретное преобразованиеФурье. Вычисление сверток
с помощью ДПФ
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)









 electronics
electronics








