Similar presentations:
Дискретное преобразование Фурье. Выделение дискретных гармоник сигнала
1. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Дискретное преобразованиеФурье. Выделение
дискретных гармоник
сигнала
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)
2. КРИТЕРИИ ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА ИЗ СМЕСИ С ШУМОМ
2Первый критерий выделения полезного сигнала
X (k )
max X (k )
X (k ) значение модуля ДПФ аддитивной смеси сигнала с шумом; порог
Второй критерий выделения полезного сигнала
X (k )
2
Pср
Pср средняя мощность аддитивной смеси
сигнала с шумом; порог
1
Pср
N
N 1
k 0
X (k )
2
3. ОПРЕДЕЛЕНИЕ ПОРОГОВ
Первый критерийmax X (k )шума
max X (k )
Второй критерий
min X (k )сигн
Pср
2
max X (k )
2
Pср
Соотношение между уровнями сигнала и шума
X (k )сигн max X (k )шума
3
4. ВОССТАНОВЛЕНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ (1)
4Спектральная плотность конечной последовательности x(n) длины N
X (e
j T
)
N 1
x(n)e j Tn
n 0
Спектральная плотность вычисляется на периоде
д 2 T
Связь спектральной плотности и ДПФ
X (k ) X (e j T )
2
k
NT
, k 0, 1, ... , N 1
Значения спектральной плотности в L равноотстоящих точках (L>N)
2
j 2 l N 1
j ln
X e L x(n)e L , l 0, 1, ... , L 1
n 0
5. ВОССТАНОВЛЕНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ (2)
5l дискретная нормированная частота
период дискретизации по частоте
д L 2π LT
Значения спектральной плотности в L равноотстоящих точках (L>N)
x(n), 0 n ( N 1);
x ( n)
N n ( L 1),
0,
X (k )
L 1
x(n)WLnk , k 0, 1, ... , L 1.
n 0
X (k )
N 1
N 1
n 0
n 0
x(n)WLnk x(n) e
j
2
kn
L ,k
0, 1, ... , L 1
6. ВОССТАНОВЛЕНИЕ АНАЛОГОВОГО СИГНАЛА (1)
6Теорема Котельникова
Любой сигнал с ограниченным спектром может быть без потерь
информации представлен набором дискретных отсчетов, взятых
через интервал T≤ 1/2fb, где
fb – верхняя граничная частота спектра аналогового сигнала.
2
j
kt
1 N 2 1
NT
x(t )
X а (k )e
,( N 2) k ( N 2 1)
N k N 2
N 2 k 1;
X ( N k ),
X а (k )
0 k ( N 2 1).
X (k ),
X а ( k ) ДПФ аналогового сигнала
X ( k ) ДПФ дискретного сигнала
7. ВОССТАНОВЛЕНИЕ АНАЛОГОВОГО СИГНАЛА (2)
Усеченный ряд Котельниковаt
sin n
N 1
T
x(t ) x(n)
t
n 0
n
T
Два способа восстановления аналогового сигнала
Формула на основе отсчетов ДПФ;
Усеченный ряд Котельникова.
7
8. ПРИМЕР (1)
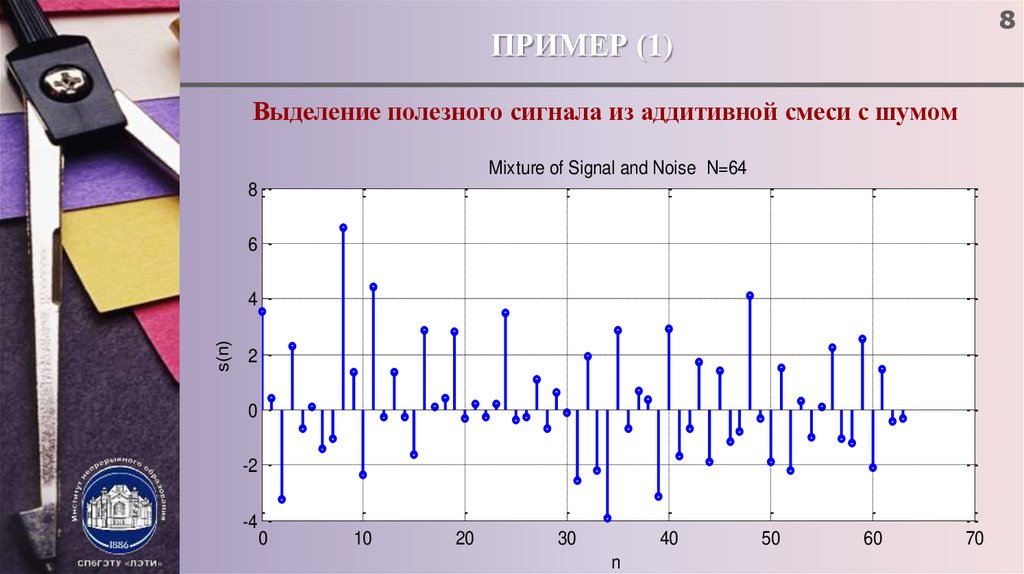
8ПРИМЕР (1)
Выделение полезного сигнала из аддитивной смеси с шумом
Mixture of Signal and Noise N=64
8
6
s(n)
4
2
0
-2
-4
0
10
20
30
40
n
50
60
70
9. ПРИМЕР (1)
9ПРИМЕР (1)
Модуль ДПФ сигнала с шумом. Применение 1-го критерия
Amplitude Spectrum N=64
|S(k)|
3
2
1
0
0
10
20
30
40
50
60
70
k
Normalized Amplitude Spectrum N=64
e1_up = 1
1
|S(k)|/max(S(k))
e1_low = 0.282
e1 = 0.3
0.5
0
0
10
20
30
40
k
50
60
70
10. ПРИМЕР (1)
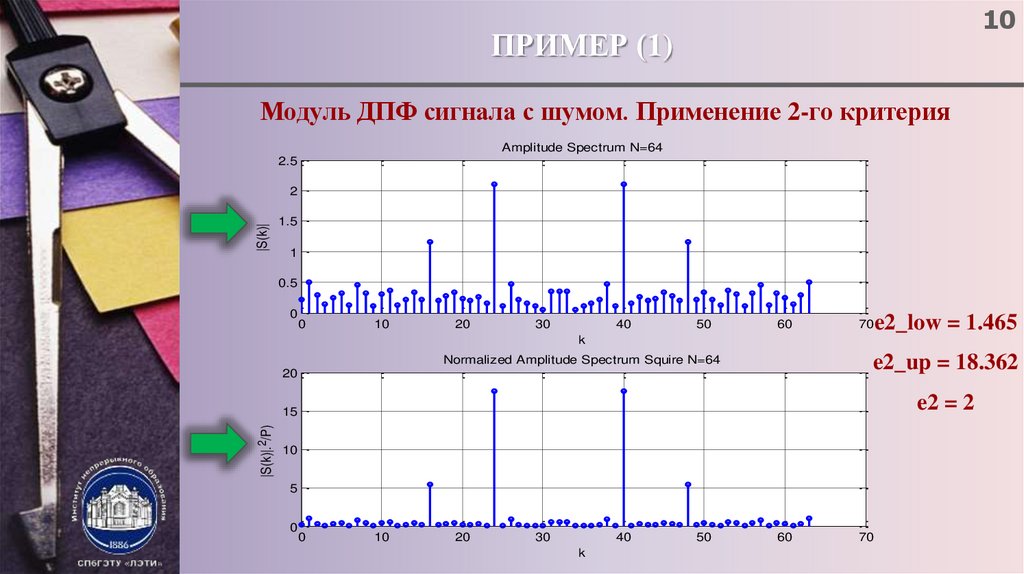
10ПРИМЕР (1)
Модуль ДПФ сигнала с шумом. Применение 2-го критерия
Amplitude Spectrum N=64
2.5
|S(k)|
2
1.5
1
0.5
0
0
10
20
30
40
50
60
70
e2_low = 1.465
k
20
e2_up = 18.362
15
e2 = 2
|S(k)|. 2/P)
Normalized Amplitude Spectrum Squire N=64
10
5
0
0
10
20
30
40
k
50
60
70
11. ПРИМЕР (2)
11ПРИМЕР (2)
Восстановление аналогового сигнала по отсчетам ДПФ
0
-5
0
20
40
60
80
n
Reconstructed Analog Signal
0
0
0.01
0.02
0.03
t
Original Analog Signal
0.04
x(t)
5
0
-5
50
0
40
60
80
k
Spectrum of Reconstructed Analog Signal
2
|Xa(k)|
x(t)
5
-5
DFT of Original Periodic Sequence N=64
100
|X(k)|
x(n)
Original Periodic Sequence N=64
5
0
0.01
0.02
t
0.03
0.04
0
20
0
-40
-20
1
0
k
20
40
12. «Методы и алгоритмы цифровой обработки сигналов на базе MATLAB»
Дискретное преобразованиеФурье. Выделение
дискретных гармоник
сигнала
Клионский Д.М. – к.т.н., доцент кафедры
математического обеспечения и применения ЭВМ (МОЭВМ)










 electronics
electronics








