Similar presentations:
Превращение энергии в колебательном движении. Гармонические колебания
1. Превращение энергии в колебательном движении. Гармонические колебания.
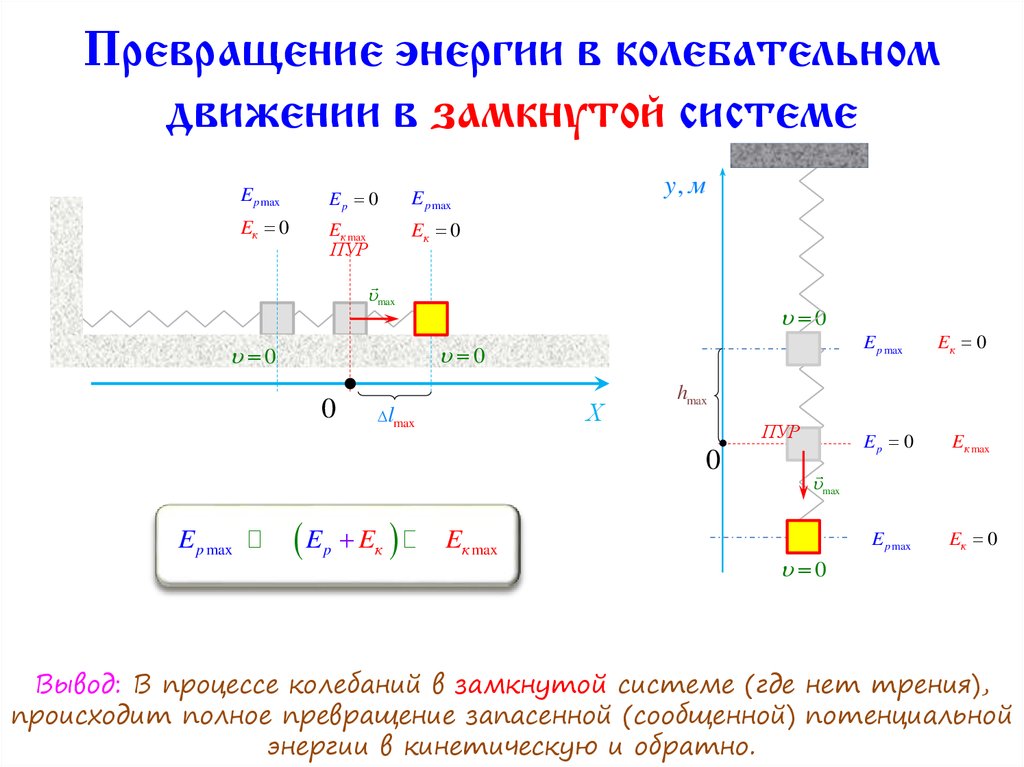
2. Превращение энергии в колебательном движении в замкнутой системе
y, мhmax
0
E p max
E p max
Eк 0
Eк 0
0
max
E p max
E
p
Eк
Eк max
0
Ep 0
Eк max
Вывод: В процессе колебаний в замкнутой системе (где нет трения),
происходит полное превращение запасенной (сообщенной) потенциальной
энергии в кинетическую и обратно.
3. Превращение энергии в колебательном движении в замкнутой системе
E p maxEp 0
E p max
Eк 0
Eк max
ПУР
Eк 0
y, м
max
0
E p max
0
0
0
Х
lmax
hmax
ПУР
0
E p max
E
p
Eк
Eк max
Eк 0
Ep 0
Eк max
E p max
Eк 0
max
0
Вывод: В процессе колебаний в замкнутой системе (где нет трения),
происходит полное превращение запасенной (сообщенной) потенциальной
энергии в кинетическую и обратно.
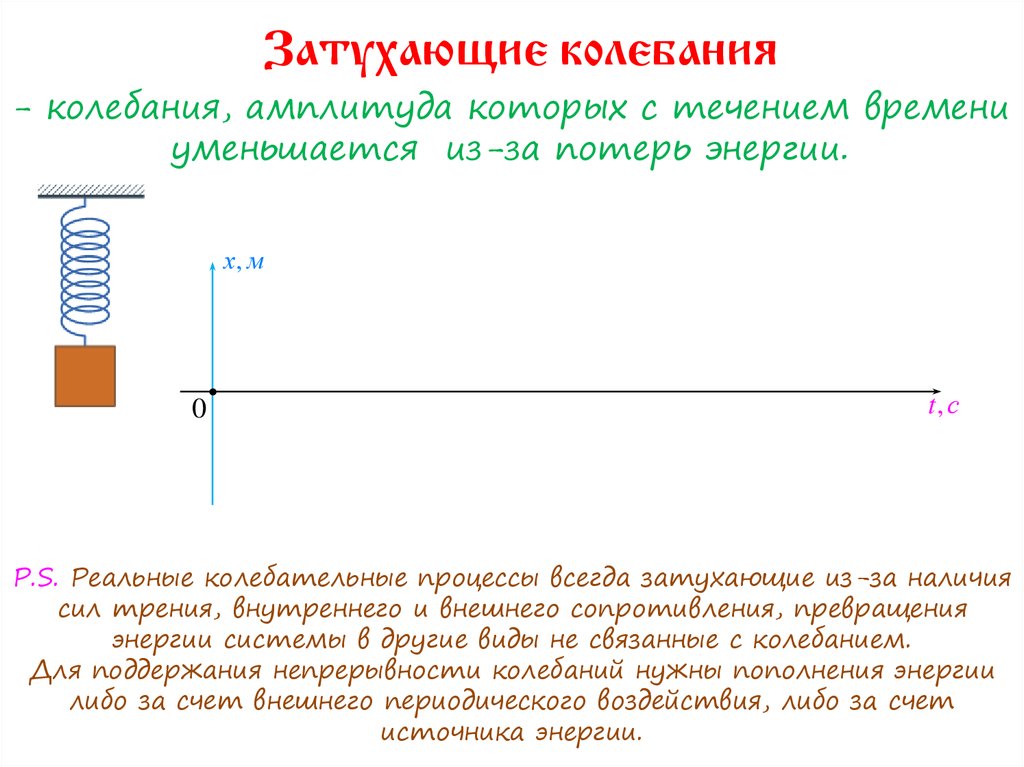
4. Затухающие колебания
- колебания, амплитуда которых с течением времениуменьшается из-за потерь энергии.
х, м
0
t, с
P.S. Реальные колебательные процессы всегда затухающие из-за наличия
сил трения, внутреннего и внешнего сопротивления, превращения
энергии системы в другие виды не связанные с колебанием.
Для поддержания непрерывности колебаний нужны пополнения энергии
либо за счет внешнего периодического воздействия, либо за счет
источника энергии.
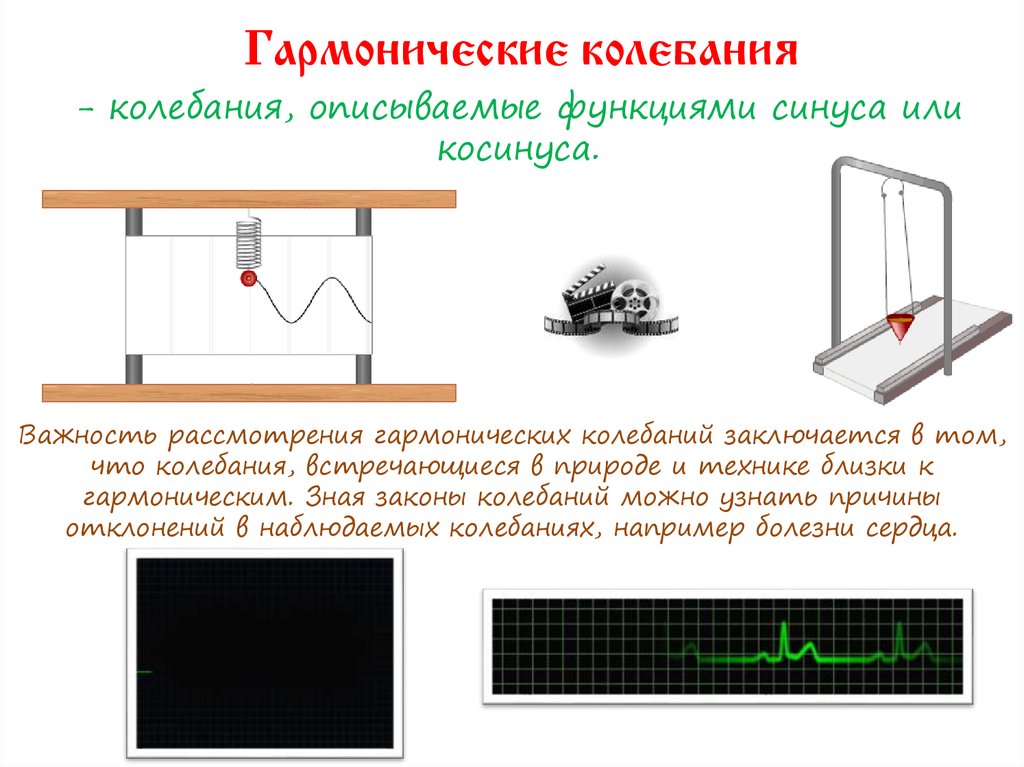
5. Гармонические колебания
- колебания, описываемые функциями синуса иликосинуса.
Важность рассмотрения гармонических колебаний заключается в том,
что колебания, встречающиеся в природе и технике близки к
гармоническим. Зная законы колебаний можно узнать причины
отклонений в наблюдаемых колебаниях, например болезни сердца.
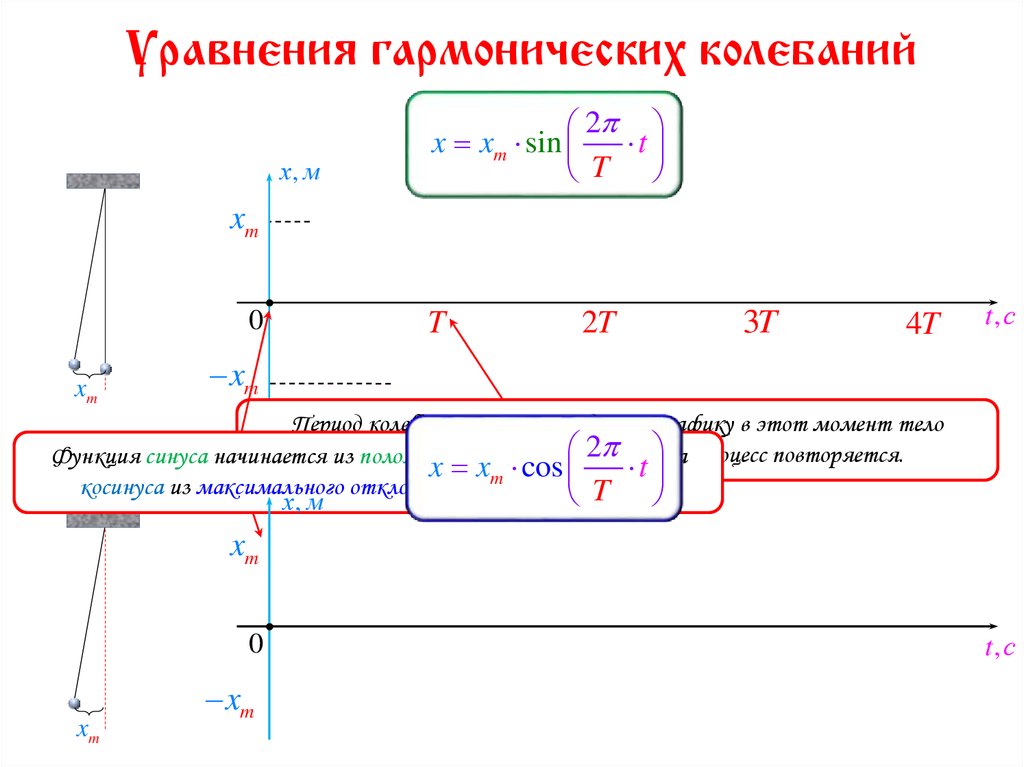
6. Уравнения гармонических колебаний
х, м2
x xm sin
t
T
xm
0
xm
T
2T
3T
4T
t, с
xm
Период колебаний тела, как видно по графику в этот момент тело
2 аи процесс повторяется.
в исходное состояние
Функция синуса начинается возвращается
из положения
x равновесия
xm cos системы,
t
косинуса из максимального отклонения тела от равновесия
T
х, м
xm
0
xm
xm
T
2T
3T
4T
t, с
7. Уравнение и график гармонических колебаний
х, мИз графика видно, что амплитуда равна 0,3 м, а период 4 с.
0,3
0
2
6
4
8
t, с
0, 3
Из графика видно что функция начинается из ноля,
2 значит
это функция синус. Запишем
Период колебаний, по определению,
когда
x xвmэто
sinвремя
t нее.тело вернется в исходное
уравнение
общем
виде
для
положение и движение повториться, по графику это хорошо видно.
T
Время 2с не подходит потому, что после него тело двигается не как после 0 секунд.
xm 0,3 м
T 4с
Подставляя данные в формулу, получаем уравнение колебаний:
2
x 0,3 sin
t 0,3 sin t 0,3 sin 1,57t
4
2
x 0,3 sin1,57t ( м)
8. Уравнение и график гармонических колебаний
Из графикавидно,
что амплитуда
равнаиз20амплитуды
см, а периодколебаний,
1 с.
Из графика
видно
что функция
начинается
значит это функция косинус Запишем уравнение в общем виде для нее.
х, см
20
0
0,5
1
1, 5
t, с
Период колебаний по определению
это время когда тело вернется в
исходное положение, по графику
это хорошо видно.
20
2
x xm cos
t
T
xm 20 см
T 1с
Подставляя данные в формулу, получаем уравнение колебаний:
2
x 20 cos
t 20 cos 2 t 20 cos 6, 28t см
1
x 20 cos 6, 28t см
9.
12
3
4
5
10. The End
11.
12.
Задача 1Определите амплитуду, период и
частоту.
s 0,5 sin 2t м
Ответ : 0,5 м; 3,Ответ
14с; 0,32 Гц
13.
Задача 2Определите амплитуду, период и
частоту.
y 5,1 cos 6, 28t м
Ответ
Ответ : 5,1
м; 1с; 1 Гц
14.
Задача 3Определите амплитуду, период и
частоту.
q 2 10 8 sin 200 t Кл
Ответ : 20 нКл;Ответ
0, 01с; 100 Гц
15.
Задача 4Определите амплитуду, период и
частоту.
i 15 10 3 cos t A
Ответ : 15 мА; 6,Ответ
28 с; 0,16 Гц
16.
Задача 5Определите амплитуду, период и
частоту колебаний. Запишите уравнение
колебаний.
S, м
2
0
2
3
6
9
12
t, c
Ответ : s 2 cos
Ответ
t ( мм)
3
17.
18.
19.
Решение №1Дано
s 0,5 sin 2t м
Решение
В общем виде уравнение выглядит:
2
s sm sin
t
T
sm ?
T ?
ν ?
Тогда, сравнивая два уравнения получаем:
sm 0,5 м
2
2
T
ν
1
T
T
ν
2
3,14 с
2
1
0,32 Гц
3,14
Ответ : 0,5 м; 3,14с; 0,32 Гц
20.
21.
Решение №2Дано
y 5,1 cos 6, 28t м
ym ?
Решение
В общем виде уравнение выглядит:
2
y ym cos
t
T
T ?
ν ?
Тогда, сравнивая два уравнения получаем:
ym 5,1 м
2
6, 28
T
ν
T
1
T
2
1с
6, 28
ν 1 Гц
Ответ : 5,1 м; 1с; 1 Гц
22.
23.
Решение №3Дано
q 2 10 8 sin 200 t Кл
qm ?
T ?
ν ?
φ0 ?
Решение
В общем виде уравнение выглядит:
2
q qm sin
t
T
Тогда, сравнивая два уравнения получаем:
qm 2 10 8 Кл 20 нКл
2
200
T
ν
1
T
T
2
0, 01 с
200
ν 100 Гц
Ответ : 20 нКл; 0, 01с; 100 Гц
24.
25.
Решение №4Дано
i 15 10 3 cos t A
Решение
В общем виде уравнение выглядит:
im ?
2
i im cos
t
T
T ?
ν ?
Тогда, сравнивая два уравнения получаем:
im 15 10 3 A 15 мА
2
1
T
ν
1
T
T
2
6, 28 с
1
ν 0,16 Гц
Ответ : 15 мА; 6, 28 с; 0,16 Гц
26.
27.
Решение №5Решение
S , мм
2
s sm cos
t
T
2
0
sm 2 мм
3
6
9
12
2
Функция косинуса начинается из
максимального отклонения тела от
равновесия
t, c
T 6с
ν
1
0,17 Гц
6
s 2 cos t ( мм)
3
Ответ : s 2 cos t ( мм)
3
























 physics
physics