Similar presentations:
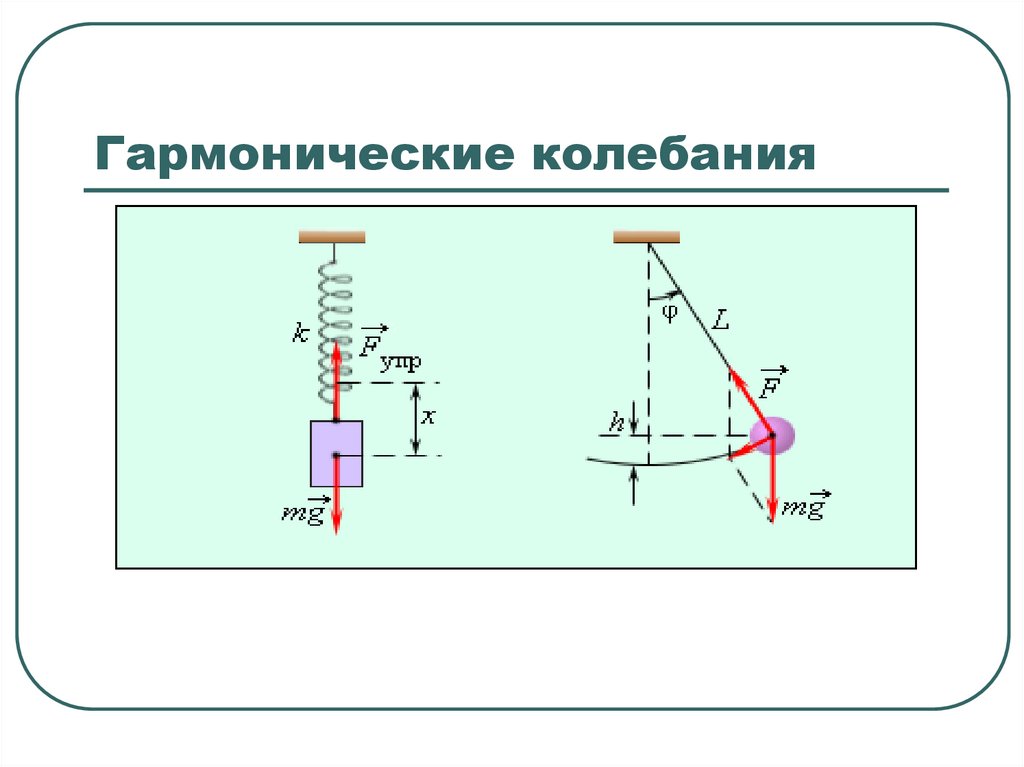
Гармонические колебания
1. Гармонические колебания
2.
Цель обучения:11.4.1.1 - исследовать гармонические
колебания (х(t), v(t), a(t))
экспериментально, аналитически и
графически
3.
4. Давайте вспомним
Колебания – …процесс, который
частично или
полностью
повторяется через
некоторый промежуток
времени.
Например, …
5. Давайте вспомним
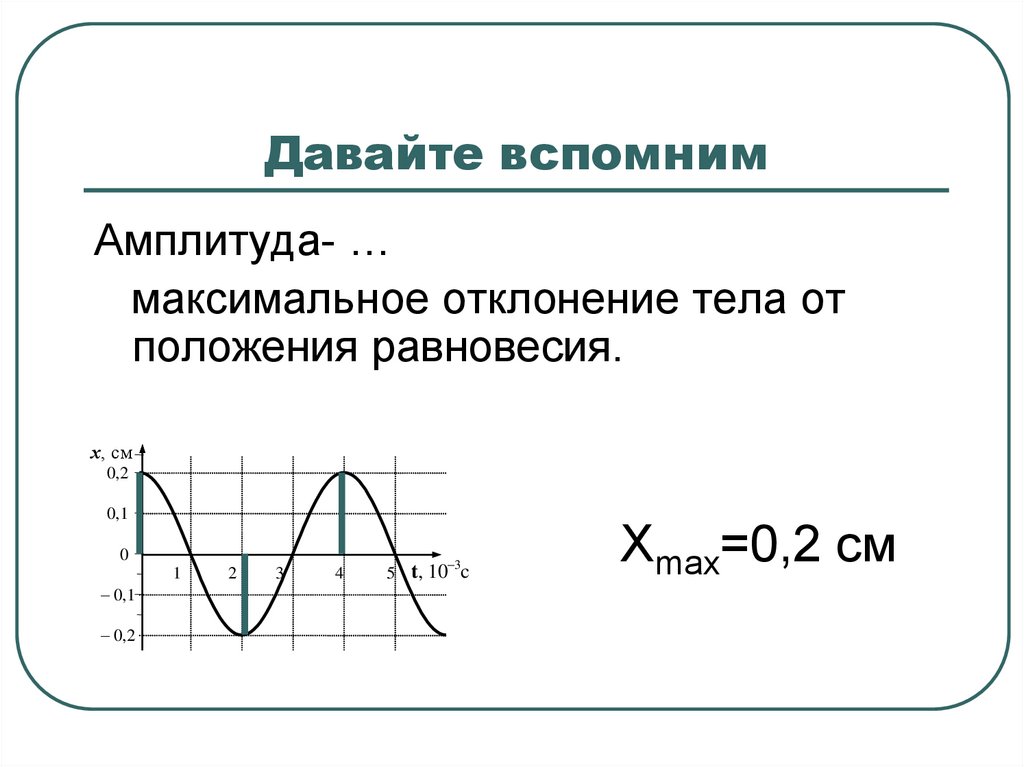
Амплитуда- …максимальное отклонение тела от
положения равновесия.
х, см
0,2
0,1
0
1
– 0,1
– 0,2
2
3
4
–3
5 t, 10 c
Хmax=0,2 см
6. Давайте вспомним
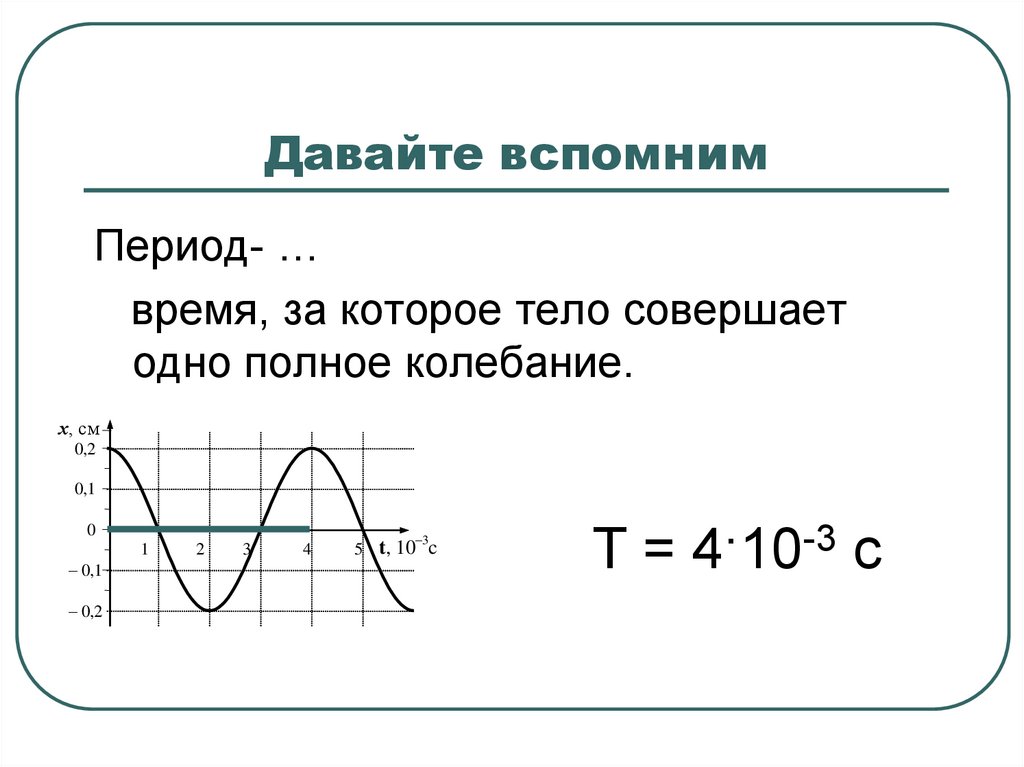
Период- …время, за которое тело совершает
одно полное колебание.
х, см
0,2
0,1
0
1
– 0,1
– 0,2
2
3
4
–3
5 t, 10 c
Т = 4·10-3 с
7. Давайте вспомним
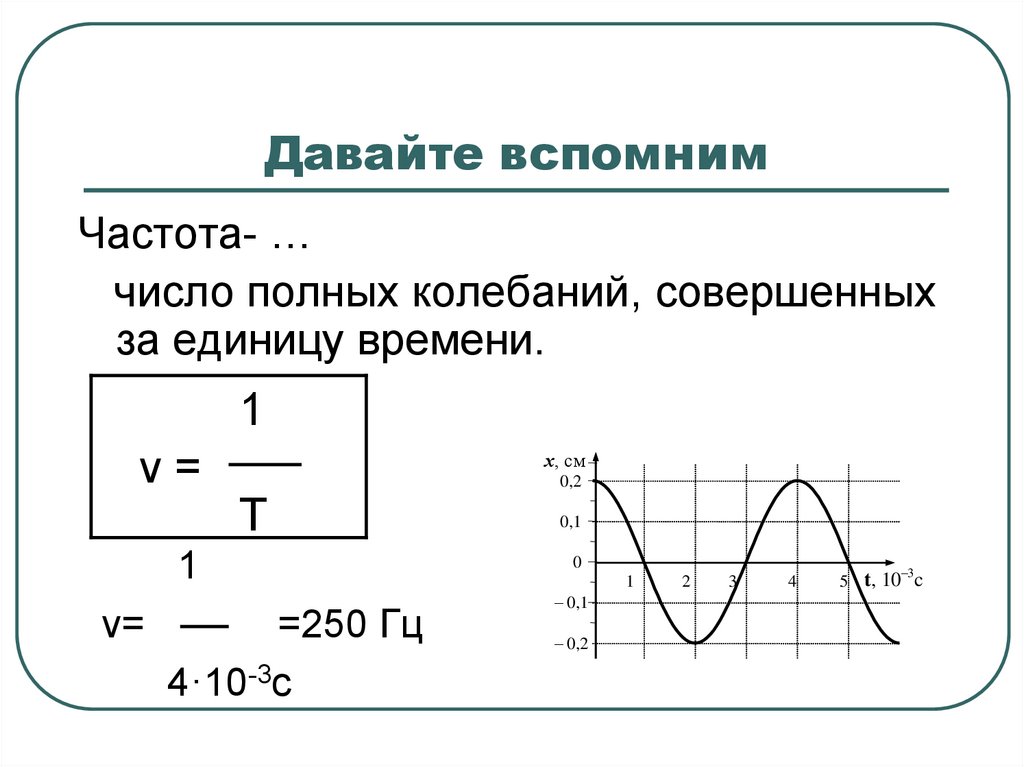
Частота- …число полных колебаний, совершенных
за единицу времени.
1
ν=
х, см
Т
1
ν=
=250 Гц
4·10-3с
0,2
0,1
0
1
– 0,1
– 0,2
2
3
4
–3
5 t, 10 c
8. Давайте вспомним
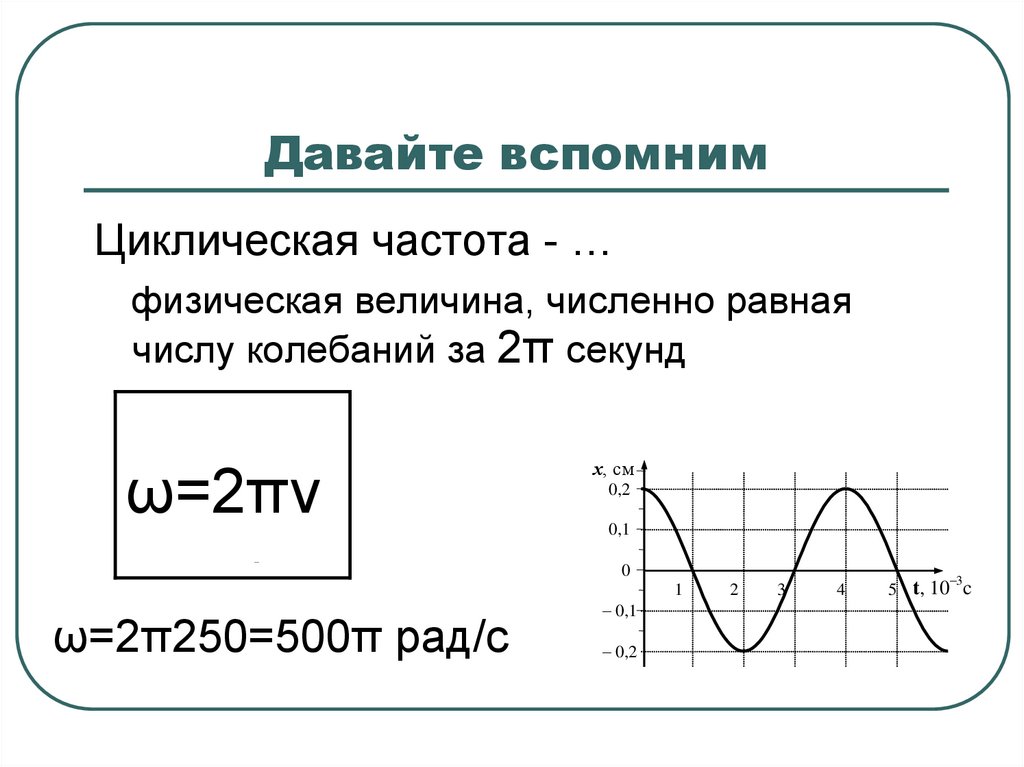
Циклическая частота - …физическая величина, численно равная
числу колебаний за 2π секунд
1
ω=2πν
Т
х, см
0,2
0,1
0
1
ω=2π250=500π рад/с
– 0,1
– 0,2
2
3
4
–3
5 t, 10 c
9. Давайте вспомним
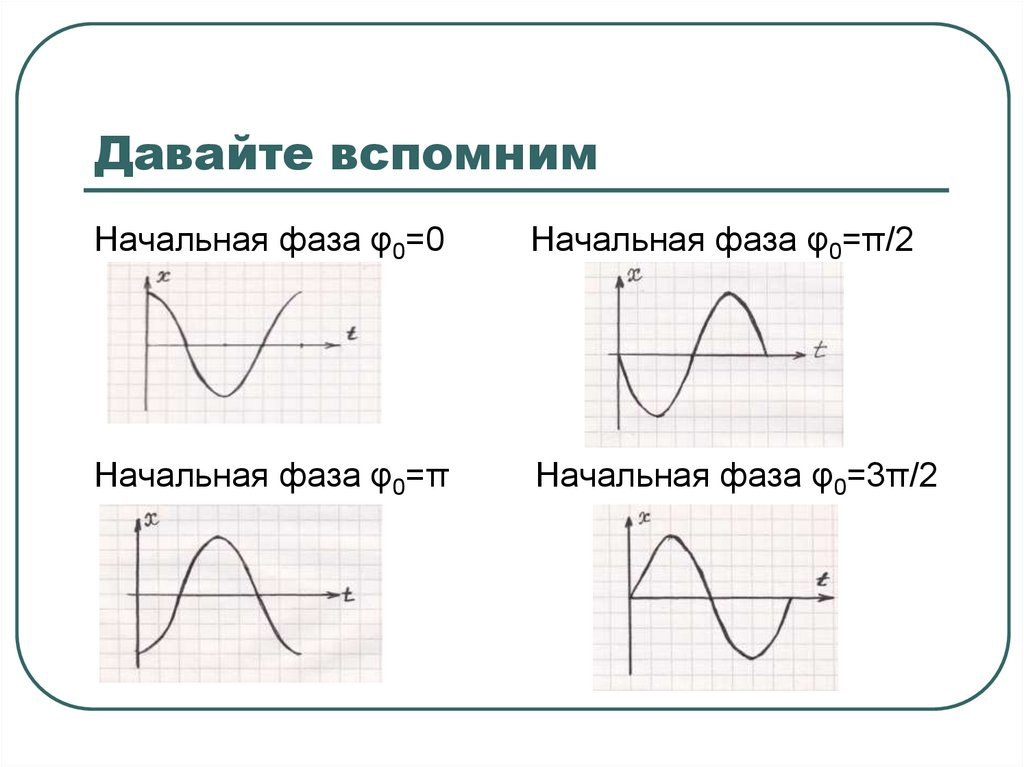
Начальная фаза φ0=0Начальная фаза φ0=π/2
Начальная фаза φ0=π
Начальная фаза φ0=3π/2
10.
Каким может быть графикгармонических колебаний?
11. Уравнение гармонических колебаний
Гармонические колебания – это колебания,происходящие по закону синуса или косинуса
Xm – амплитуда колебаний
x = xm cos (ωt + φ0)
φ0 – начальная фаза колебаний
ω – циклическая частота
ω=2πν
φ = ωt + φ0 – фаза колебаний в
данный момент времени
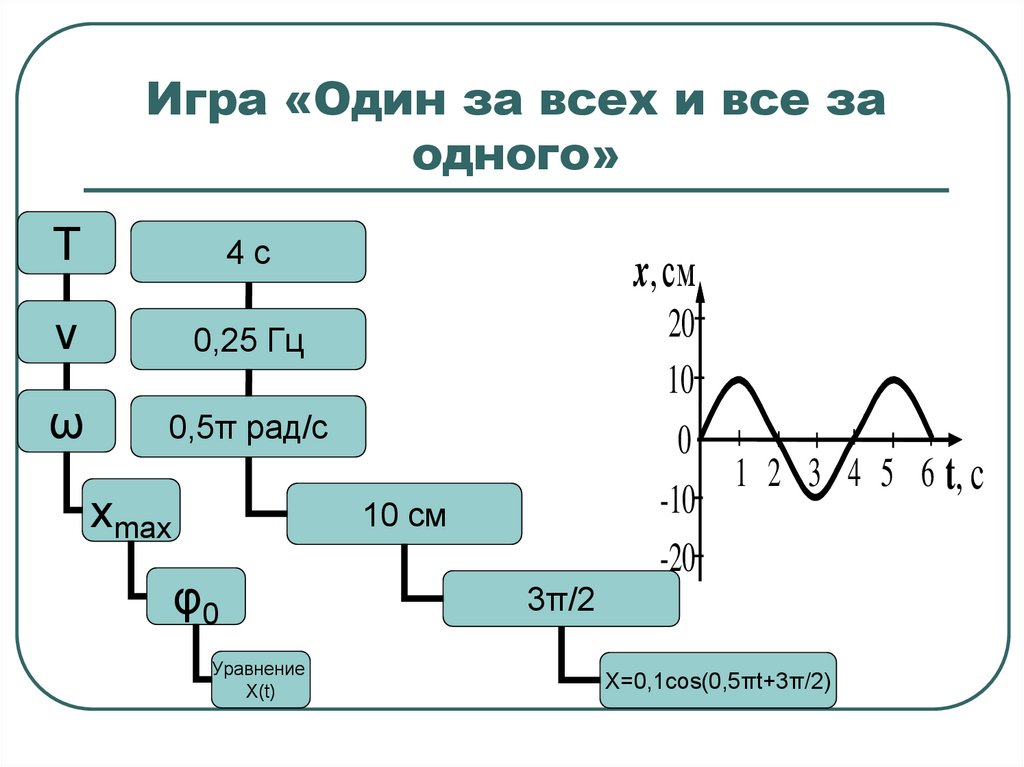
12. Игра «Один за всех и все за одного»
Т4с
ν
0,25 Гц
ω
0,5π рад/с
хmaх
x, см
20
10
0
1 2 3 4 5 6 t, c
-10
-20
10 см
φ0
Уравнение
Х(t)
3π/2
Х=0,1соs(0,5πt+3π/2)
13. Уравнение гармонических колебаний
Гармонические колебания – это колебания,происходящие по закону синуса или косинуса
Xm – амплитуда колебаний
x = xm cos (ωt + φ0)
φ0 – начальная фаза колебаний
ω – циклическая частота
ω=2πν
φ = ωt + φ0 – фаза колебаний в
данный момент времени
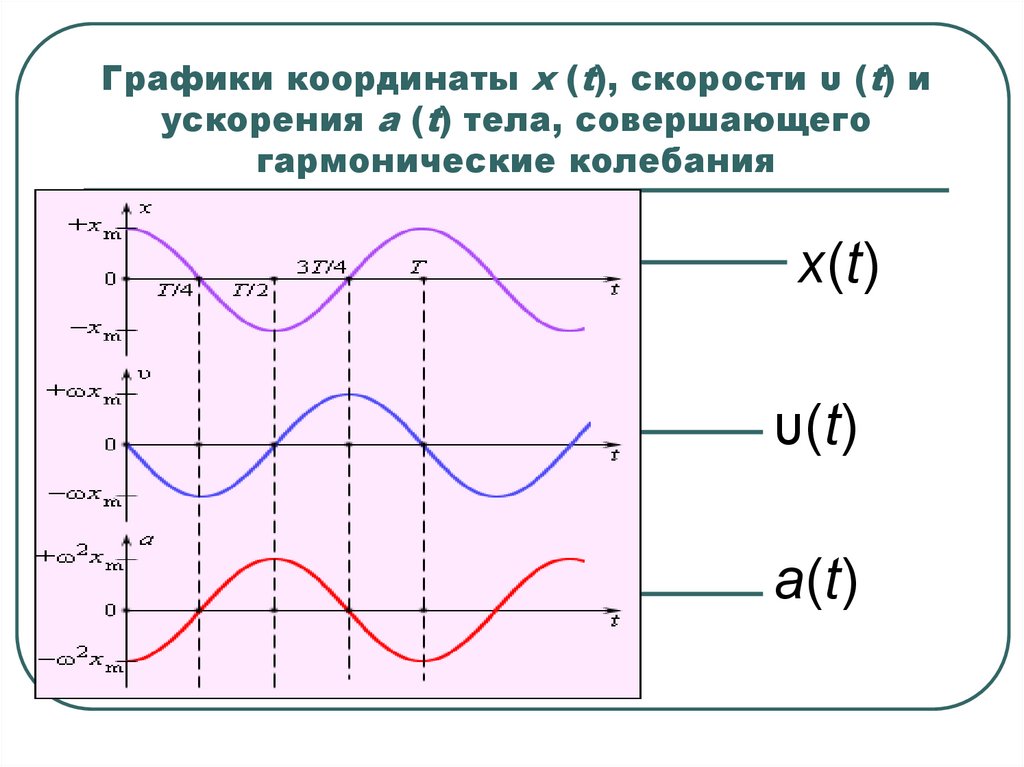
14. Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания
Графики координаты x (t), скорости υ (t) иускорения a (t) тела, совершающего
гармонические колебания
x(t)
υ(t)
a(t)






 physics
physics








