Математический анализ. Повтор лекций

1. Математический анализ

Лекция -6ю
1

2.

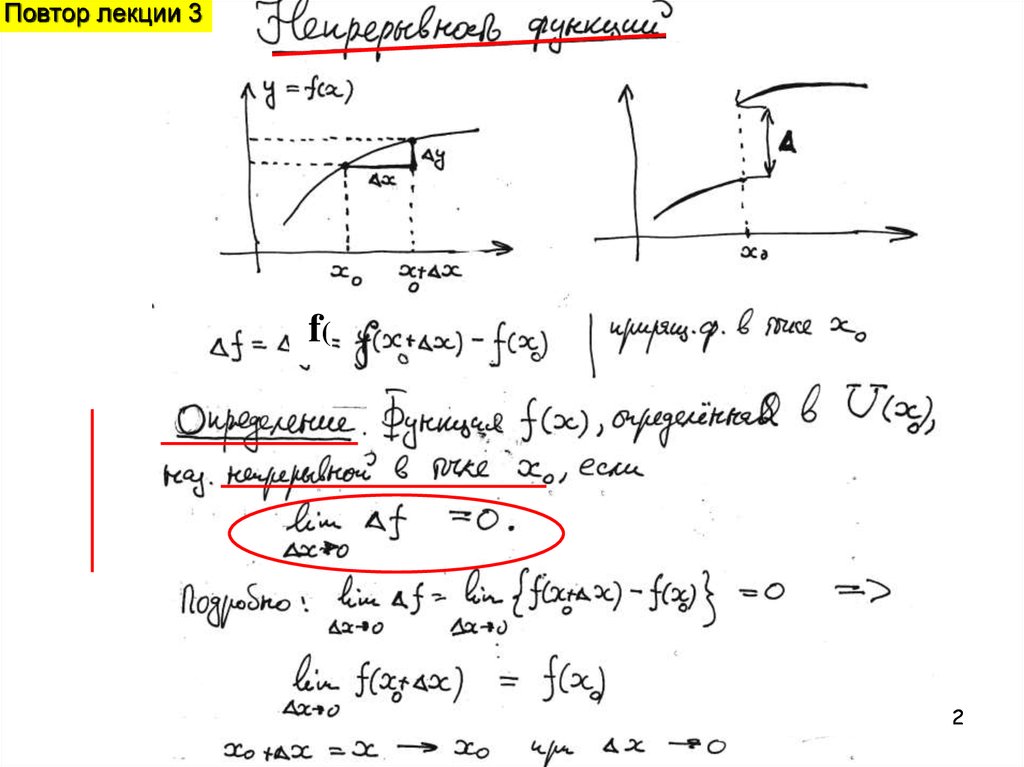
Повтор лекции 3
f(
2

3. .

Повтор лекции 4
.
Производная функции
Таким образом, приходим к важнейшему понятию :
Определение.
Пусть ф. f(x) определена в окр. т. x U(x)
Процедура вычисления производной наз.
дифференцированием
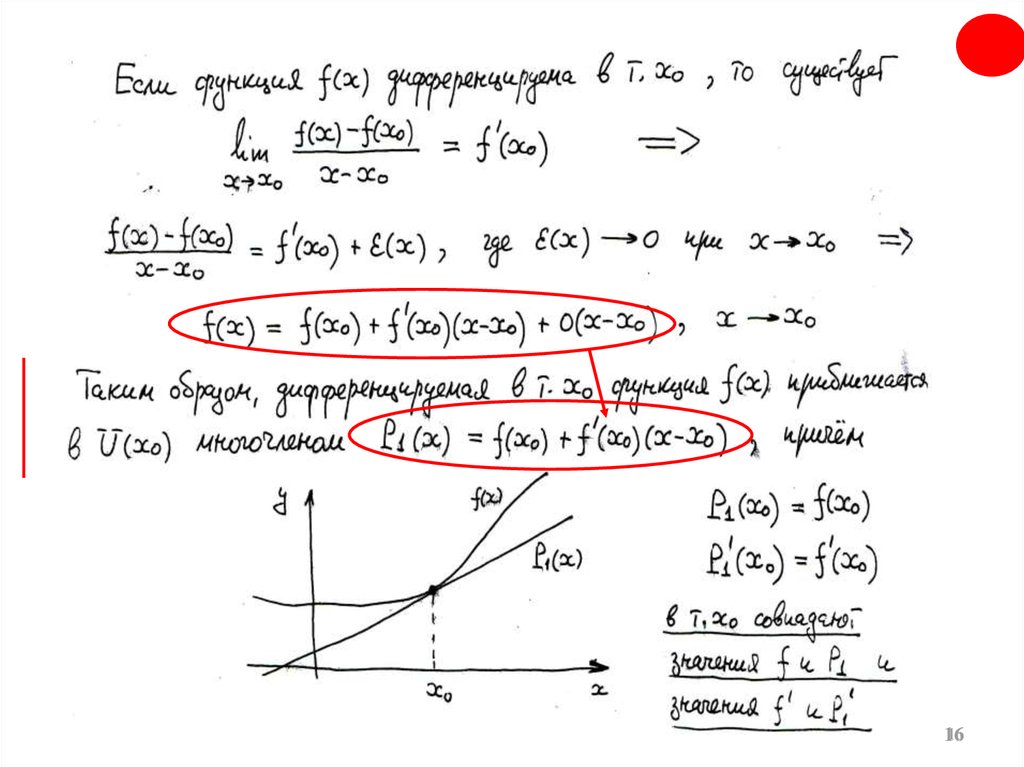
3

4. .

наз. предельное положение секущей при P
M
k
f (a)
4

5.

Повтор лекции 4
Производная сложной функции
5

6.

Повтор лекции 4
Дифференциал функции
6

7.

Повтор лекции 5
Основные теоремы
дифференциального исчисления
7

8.

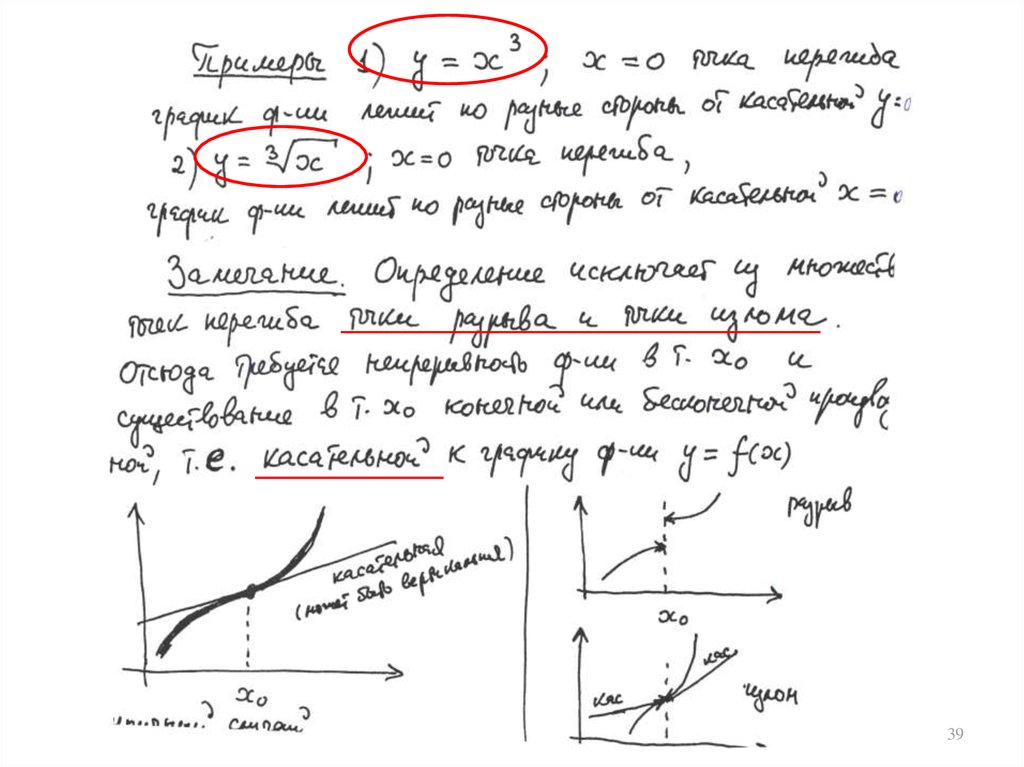
1
нет локального экстремума!
8

9.

2
по 2-й т. Вейерштасса
по т. Ферма
(слайд №11)
9

10.

3
10

11.

4
11

12.

Правило Лопиталя-Бернулли
Теорема
)
тогда
х)
12

13.

)
13
)

14.

14

15.

Формула Тейлора (Taylor)
Формула Тейлора является одной из жемчужин математического
анализа и широко используется и в теоретических исследованиях, и
вычислительной практике. Эта формула позволяет адекватно
заменить заданную сложным выражением функцию удобным для
анализа многочленом.
______
Сл №18
15

16.

16
16

17.

Форма Пеано
_____________
n
n
17

18.

Сл №26
18

19.

19

20.

1
2
3
20

21.

4
Продолжени
е
5
21

22.

Вычисление пределов по формуле Тейлора
)
см. слайд №20-21
22

23.

n!
23

24.

и
нж
Форма Пеано
см. сл.15
24

25.

_____
25

26.

26

27.

(см.сл №7)
27

28.

Локальные экстремумы
Из теоремы Ферма следует
28

29.

Теорема (первый дост. признак строгого лок. экстремума в крит. точке)
Пусть f(x) – дифференцируема в U(xо ) и непрерывна в т. хо
1
___________
Аналогично случай
29
2

30.

30

31.

Теорема (2-й дост.
признак строгого
лок. экстремума )
__________________
31

32.

32

33.

Продолжение
33

34.

34

35.

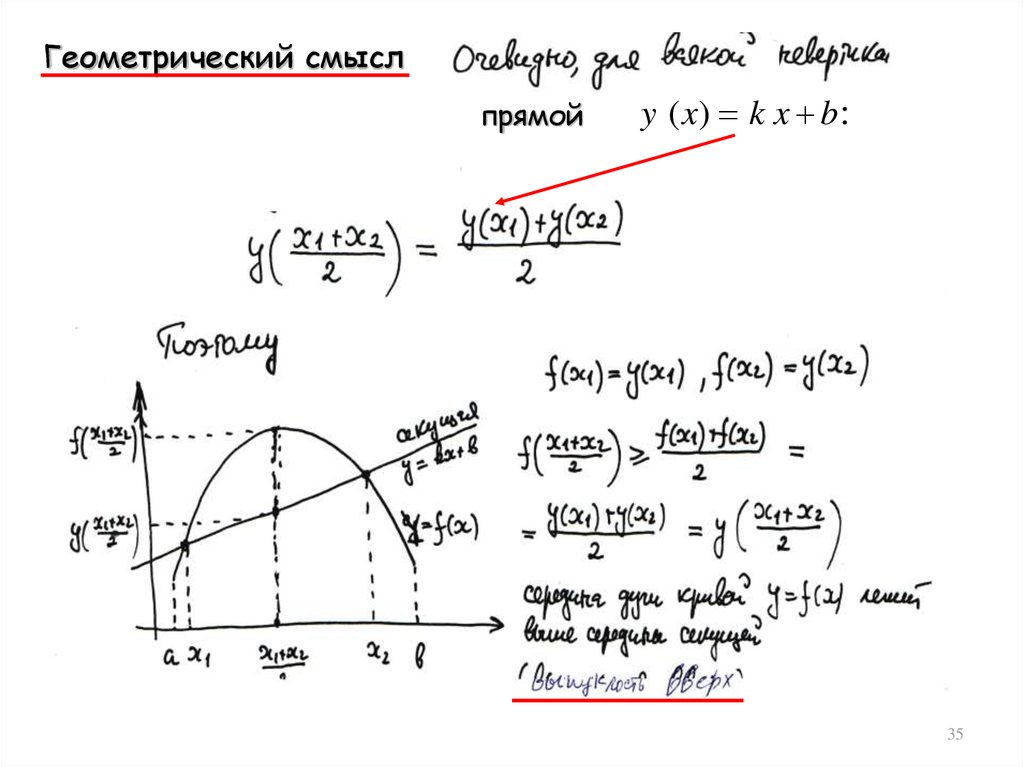
Геометрический cмысл
прямой
y ( x) k x b :
35

36.

2
36

37.

37

38.

38

39.

39

40.

40

41.

41

42.

42

43.

43

44.

Схема
построения
графиков
Таблица
поведения
функции
44

45.

45

46.

Спасибо за внимание
46

47.

Спасибо за внимание !
47