Производная функции

1. Математический анализ

Лекция -4(ю)
Производная функции
1

2.

Предел функции
Повтор лекции 2
определена
Пример :
f ( x)
3
1
x sin x
в точке x = 0 не определена , но
lim f ( x) 2 0
x 0

3.

Первый замечательный предел
Рассмотрим окружность единичного радиуса, х - центральный угол, 0 < x <
Повтор лекции 2
/2
3

4.

Повтор лекции 2
.
1
При этом xn xn 1 , т.е. последовательность {xn } 1
n
возрастает и она ограничена :
xn 2
1
1
1
2 ... n 1 2
1
2 2
2
1 (1 1 )
2
2n 1
1 12
следовательно 2 xn 3 , n
3
n
1
2 n. 1
4

5.

Повтор лекции 2
5

6.

Повтор лекции 2
6

7.

Повтор лекции 3
f(
7

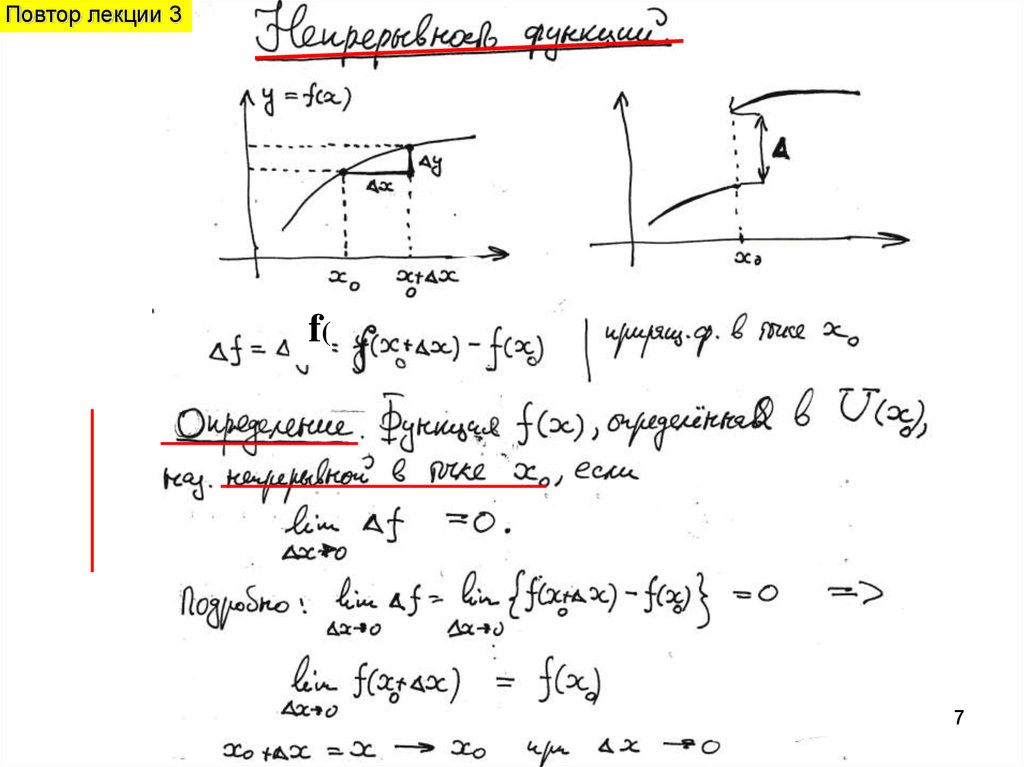
8. Непрерывные функции

Повтор лекции 3
Непрерывные функции
Непрерывность функции f(x) в окрестности т. a
сформулируем на языке приращений f(x) от приращения
аргумента x :
Рис.3
положительны.
Поскольку
8
8

9.

Повтор лекции 3
.
10
10
9

10.

Повтор лекции 3
Непрерывные функции в т очке
10

11.

Повтор лекции 3
1
5
2
3
4
11

12.

Повтор лекции 3
.
12

13. Односторонние пределы.

Повтор лекции 3
Односторонние пределы.
13

14. Продолжение.

Если
14
14

15. Свойства непрерывных функций

Рис. 9.6
15
15

16. .

16

17.

17

18. .

18

19.

19

20.

Производная функции
В
20

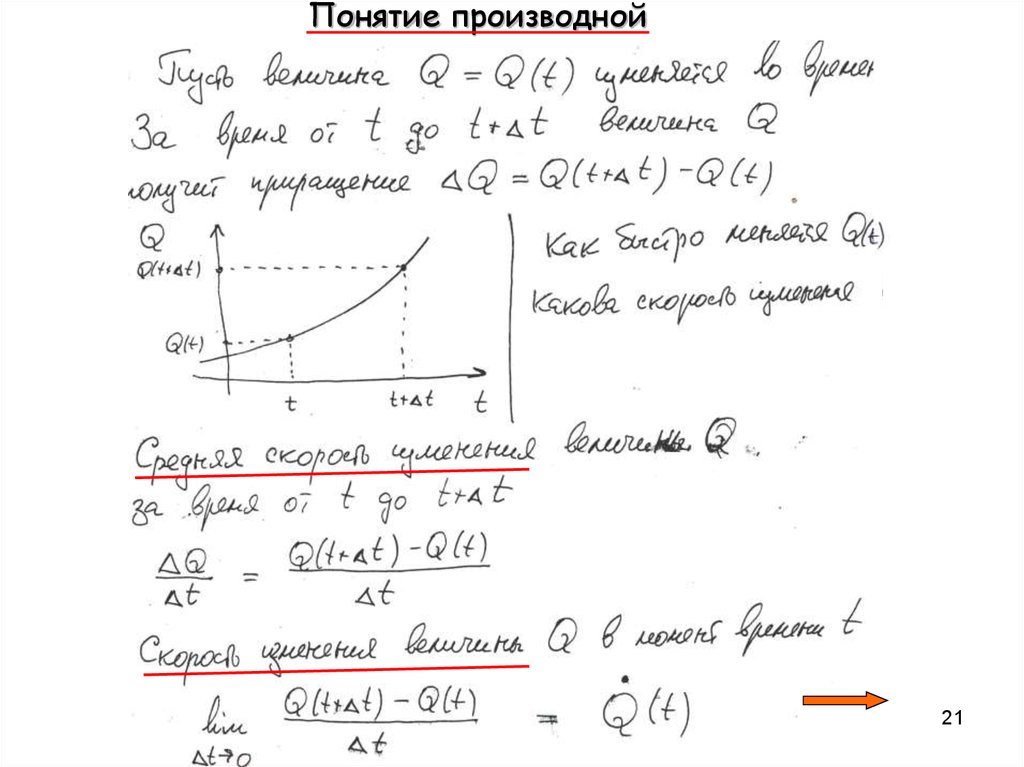
21. Понятие производной

21

22. .

Таким образом, приходим к важнейшему понятию :
Определение.
Пусть ф. f(x) определена в окр. т. x U(x)
Процедура вычисления производной наз.
дифференцированием
22

23. .

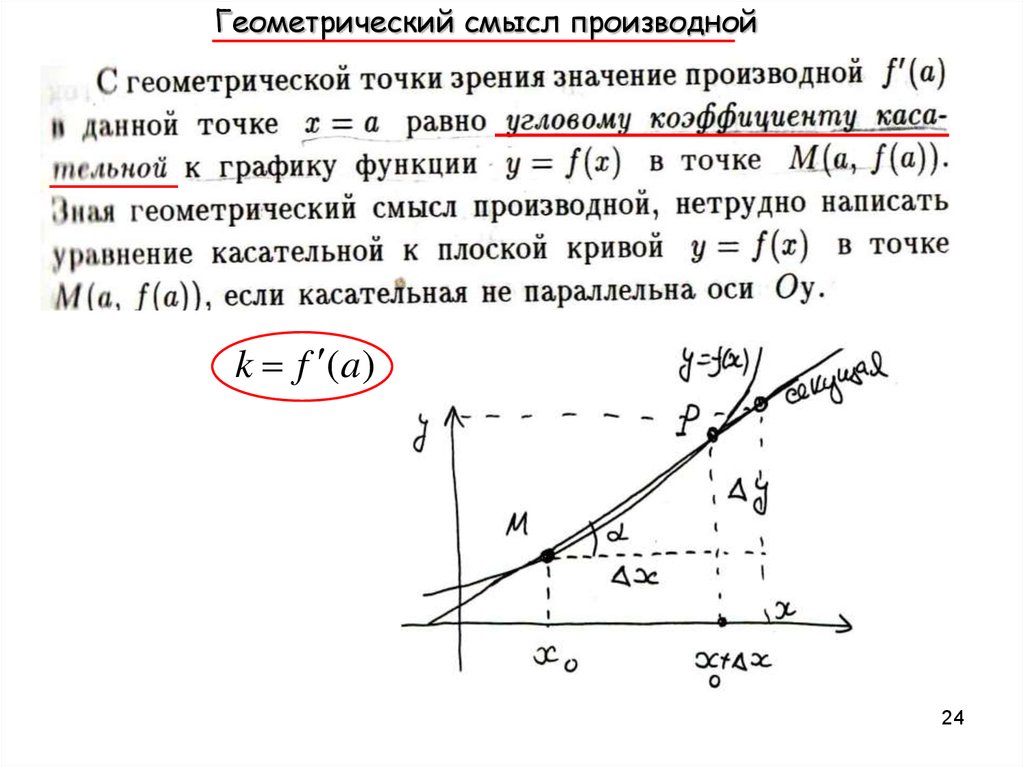
наз. предельное положение секущей при P
M
k
f (a)
23
23

24.

Геометрический смысл производной
k f (a)
24

25. Уравнение нормали в точке

Прямая, проходящая через точку М и перпендикулярная к
касательной, наз. нормалью к графику функции y = f(x) в
т. М (прямая NM ). Если
f (a ) 0 , то уравнение
нормали имеет вид
y f (a) ( x a) / f (a)
В случае f ( a ) 0 , нормаль вертикальна, т.е. ее
уравнение будет
x=a
25

26.

26
26

27.

Дифференцируемость функций
27
27

28.

28

29.

29

30.

Продолжение
30

31.

31
31

32.

32
32

33.

33

34.

Производные обратных элементарных функций
34

35.

Продолжение
35

36.

36

37.

Спасибо за внимание
37
37

38.

А.С. Монин, Н.Н. Корчагин
Десять открытий
в физике океана
Прикладная математика
38и
. открытия в Мировом океане

39.

39

40.

40
40

41.

.
41

42.

.
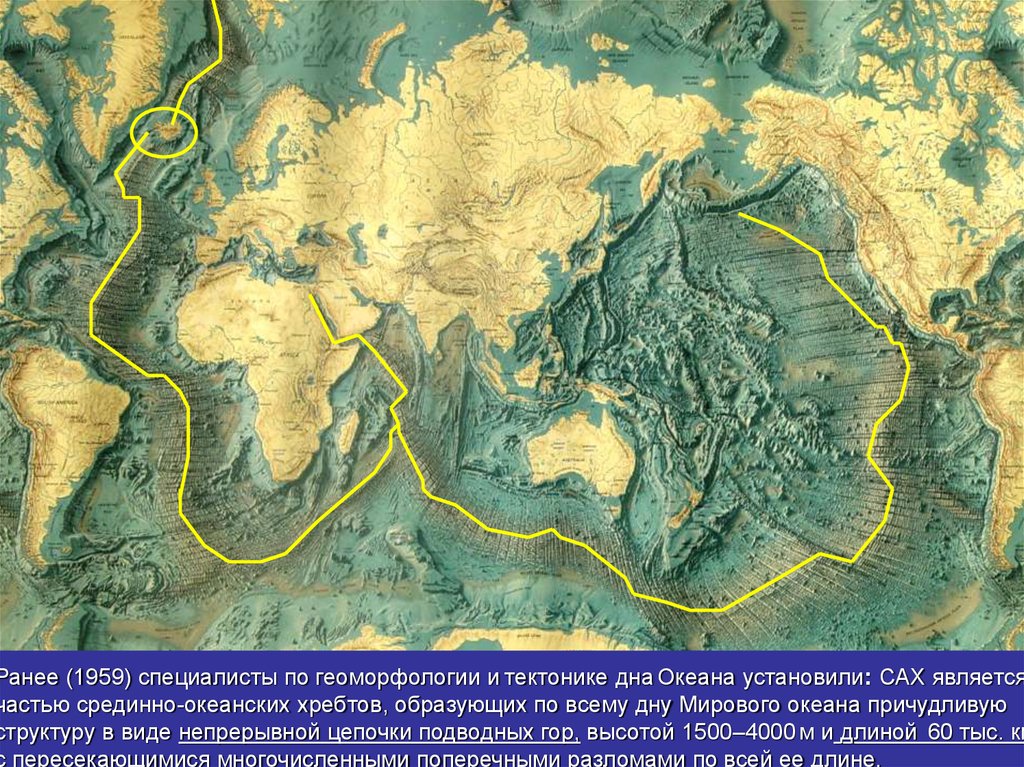
Ранее (1959) специалисты по геоморфологии и тектонике дна Океана установили: САХ является
частью срединно-океанских хребтов, образующих по всему дну Мирового океана причудливую
42
структуру в виде непрерывной цепочки подводных гор, высотой 1500–4000 м и длиной 60 тыс. км
с пересекающимися многочисленными поперечными разломами по всей ее длине.

43.

43

44.

44