Метод параллельного переноса решения геометрических задач

1.

2.

Это определение оправдано тем, что отображение, удовлетворяющее указанным в нем
двум требованиям, отображает плоскость на себя и обратно, т.е. является
преобразованием плоскости
Теорема. Перенос есть движение.
ЕслиТr(М) = М и Тr(N) = N, тоMM=NN=r
Следовательно, MM' + M'N = M'N + NN', или MN = M'N' и, значит, MN =
M'N'
Сравнение ориентаций двух соответственных при переносе треугольников
показывает, что перенос является движением первого рода

3.

Любой параллельный перенос можно представить как композицию двух
осевых симметрий с параллельными осями, причем направление осей
перпендикулярно переносу, а расстояние между ними равно половине его
длины.

4.

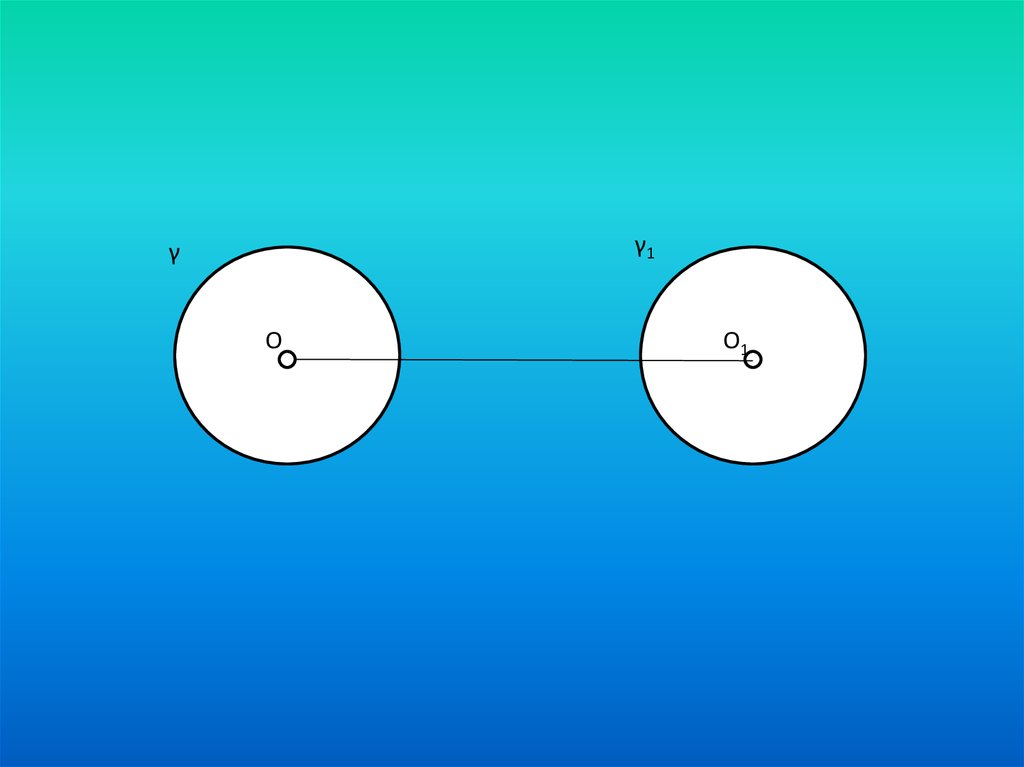
ЗАДАЧА.
Постройте прямую, которая пересекает по равным хордам два равных круга.
Дано: γ (О,r); γ1 (O, r).
Анализ.
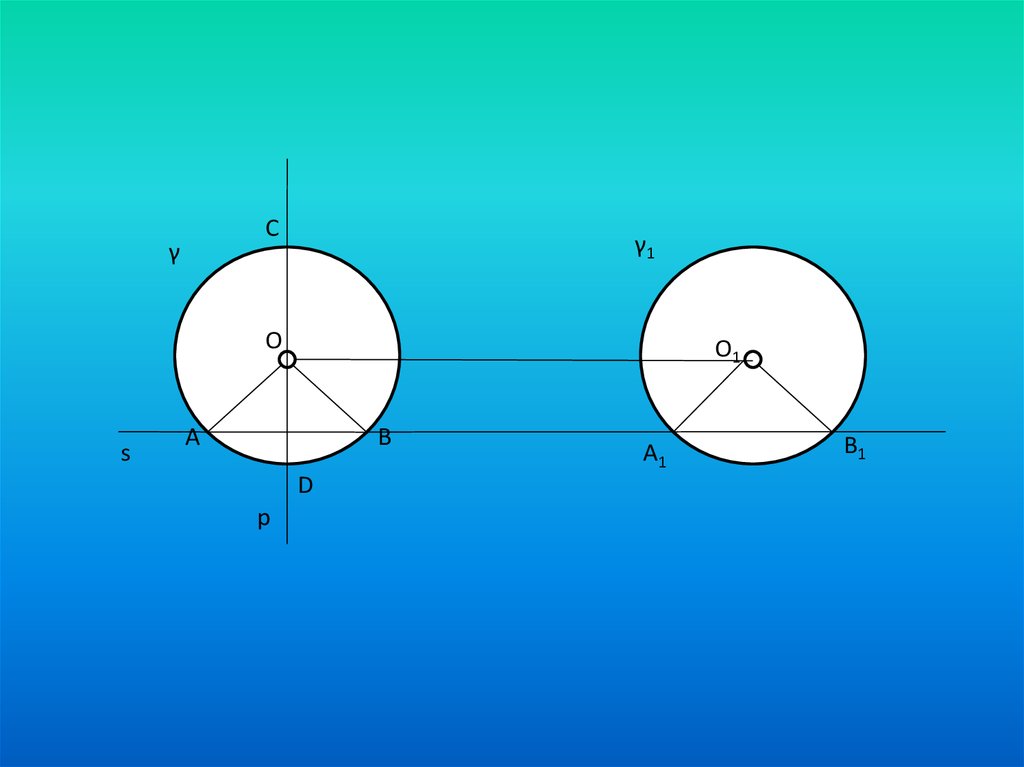
Пусть s – искомая прямая, тогда s ∩ γ = {A,B}, s ∩ γ1 = {A1, B1} и АВ = А1В1.
Тогда ∆АОВ = ∆А1О1В1 (ОА = О1А1 = r, ОВ = О1В1 = r, АВ = А1В1), отсюда ОАВ =
О1А1В1;
но А, В, А1, В1 є s, следовательно, ОА || О1А1.
Поэтому АОО1А1 – параллелограмм ( ОА = О1А1, ОА || О1А1), отсюда s || ОО1
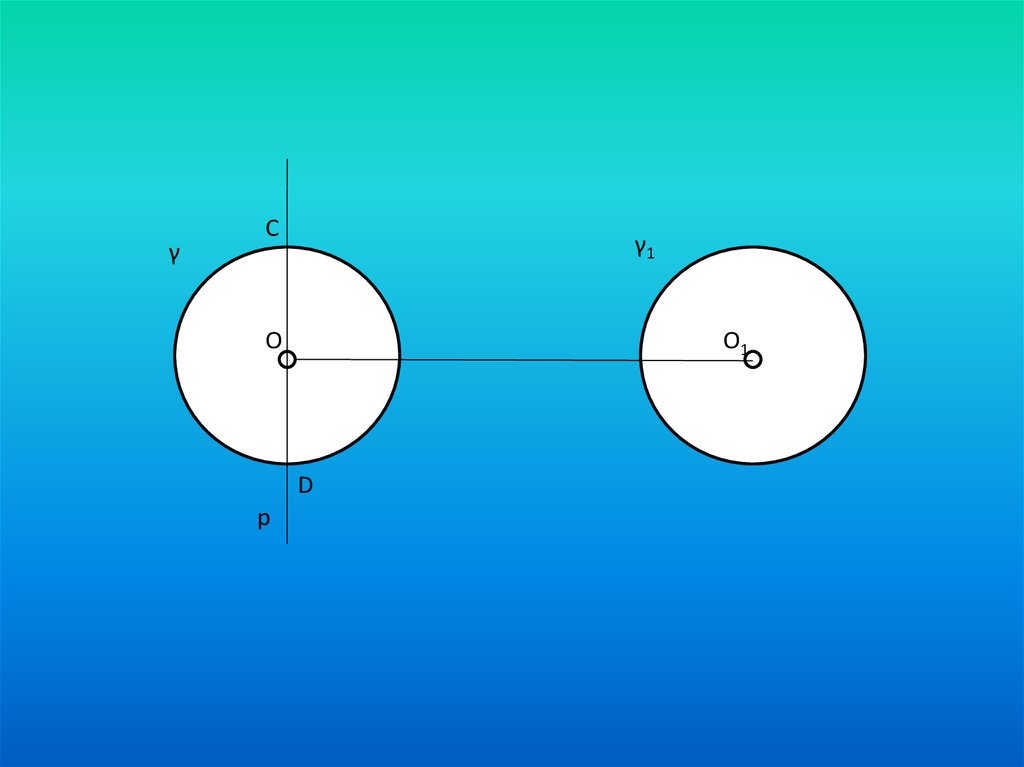
Построение.
1.ОО1
2.р: О є р, р ОО1
3.р ∩ γ = {C, D}.
4.А: А є γ, А ≠ C, D.
5.s: A є s, s || OO1
6.s – искомая прямая.

5.

γ1
γ
О
О1

6.

γ1
γ
О
О1

7.

γ
C
γ1
О
О1
D
р

8.

C
γ
γ1
О
s
О1
А
В
D
р
А1
В1

9.

Доказательство.
Рассмотрим параллельный перенос Т1 на вектор ОО1, имеем, что Т1: О→О1,
γ (О, r) → γ1(О,r); кроме того, Т1: s→s, поэтому при Т1 точки {А,В} = s ∩ γ переходят в
точки {А1, В1} = s ∩ γ1, а именно: Т1: А→А1, В→В1, отсюда АВ = А1В1
Исследование.
Задача имеет бесконечное множество решений, так как способов выбрать точку А
бесконечно много.