Методы решения геометрических задач. ЕГЭ, задание С2 (Расстояние от точки до плоскости)

1.

(Расстояние от точки до плоскости)
Подготовил:
учитель математики
МОУ «СОШ №10 с. СолдатоАлександровского»
Кобзев Д.А.
2012 – 2013 уч.г.

2.

Расстояние от точки до плоскости
Методы
Поэтапно-вычислительный
метод
Метод параллельных
прямых и плоскостей
Векторный метод
Координатный метод
Метод объемов

3.

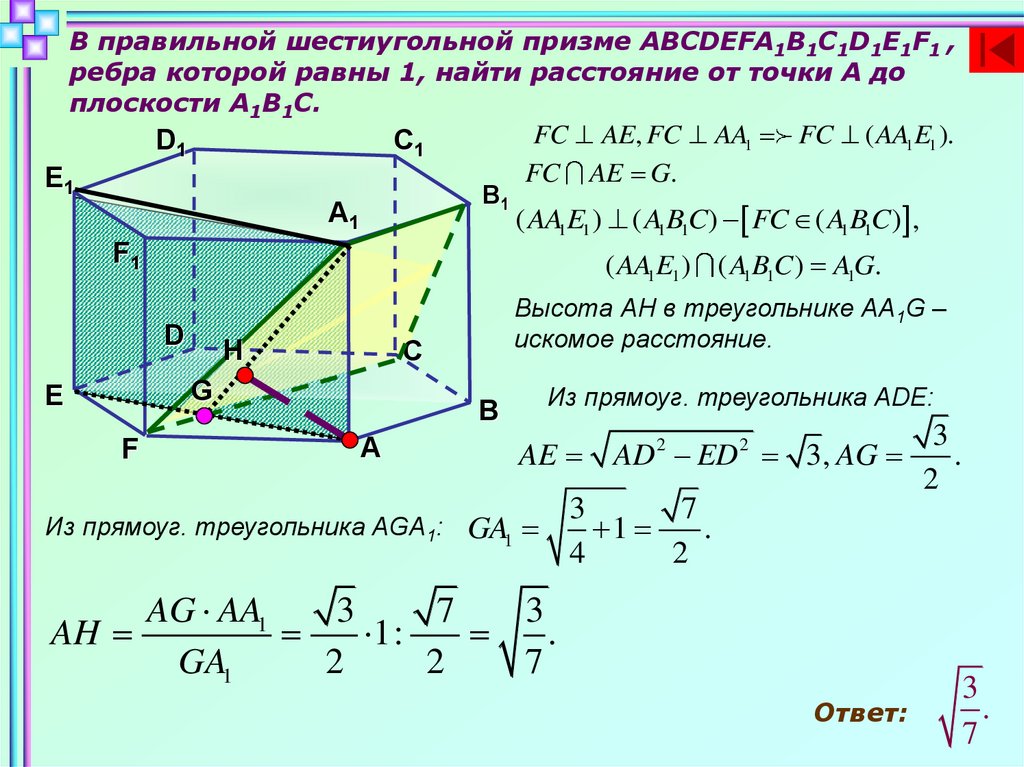
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ,
ребра которой равны 1, найти расстояние от точки А до
плоскости А1В1С.
FC AE, FC AA1 FC ( AA1E1 ).
D
C
1
1
E1
B1
A1
FC
( AA1E1 ) ( A1B1C) FC ( A1B1C) ,
F1
( AA1E1 ) ( A1B1C ) AG
1 .
D
H
F
Высота АН в треугольнике АА1G –
искомое расстояние.
C
G
E
AE G.
Из прямоуг. треугольника ADE:
B
A
Из прямоуг. треугольника AGA1:
AE AD 2 ED 2 3, AG
GA1
3
.
2
3
7
1
.
4
2
AG AA1
3
7
3
AH
1:
.
GA1
2
2
7
Ответ:
3
.
7

4.

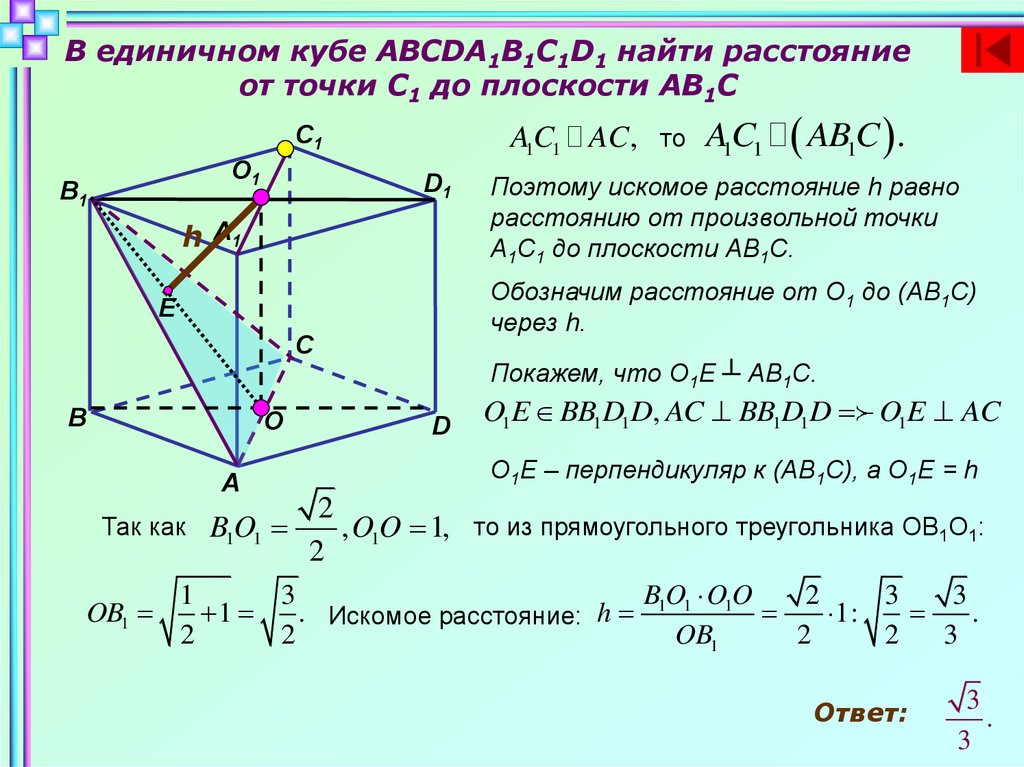
В единичном кубе ABCDA1B1C1D1 найти расстояние
от точки C1 до плоскости AB1C
A1C1 AC , то AC
1 1
C1
О1
B1
D1
h A1
C
О
A
Поэтому искомое расстояние h равно
расстоянию от произвольной точки
А1С1 до плоскости АВ1С.
Обозначим расстояние от О1 до (АВ1С)
через h.
Е
B
AB1C .
Покажем, что О1Е ┴ АВ1С.
D
O1E BB1D1D, AC BB1D1D O1E AC
О1Е – перпендикуляр к (АВ1С), а О1Е = h
2
Так как B1O1
, O1O 1, то из прямоугольного треугольника ОВ1О1:
2
OB1
B O O O
2
3
3
1
3
1:
.
1
. Искомое расстояние: h 1 1 1
OB1
2
2
3
2
2
Ответ:
3
.
3

5.

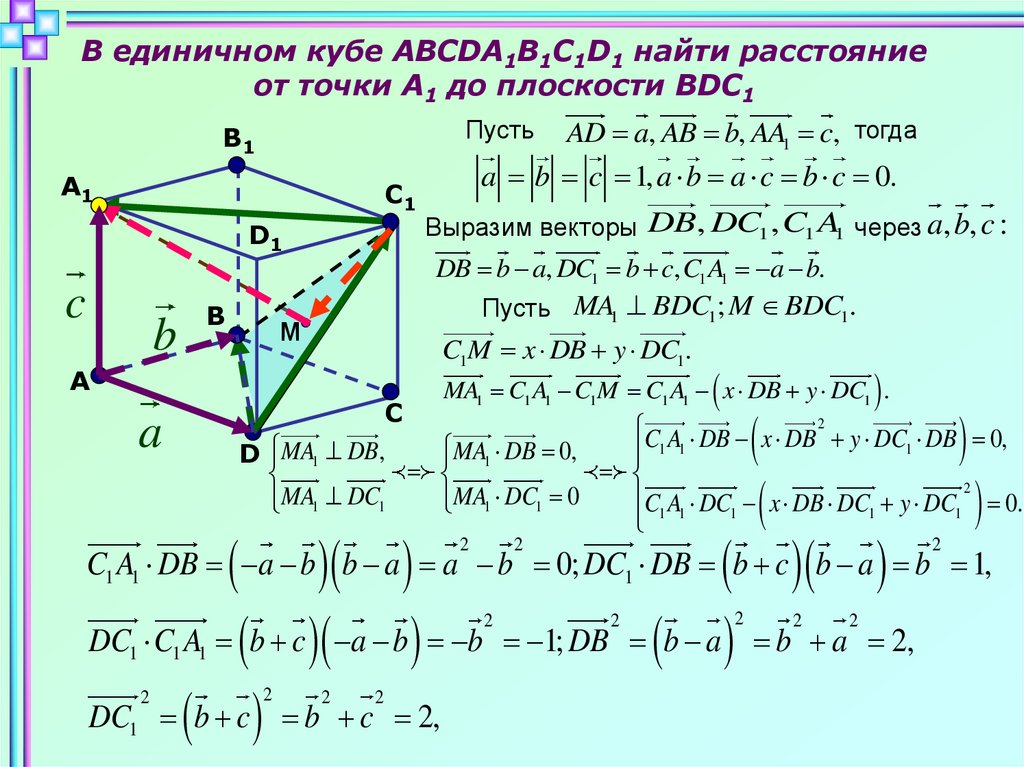
В единичном кубе ABCDA1B1C1D1 найти расстояние
от точки А1 до плоскости BDC1
Пусть
B1
A1
C1
D1
c
b
B
a b c 1, a b a c b c 0.
Выразим векторы DB, DC1 , C1 A1 через a, b, c :
DB b a, DC1 b c, C1 A1 a b.
Пусть MA1 BDC1 ; M BDC1.
M
C1M x DB y DC1.
A
C
D MA1 DB,
MA1 DC1
a
AD a, AB b, AA1 c, тогда
MA1 C1 A1 C1M C1 A1 x DB y DC1 .
C A DB x DB 2 y DC DB 0,
1
MA1 DB 0,
1 1
2
C1 A1 DC1 x DB DC1 y DC1 0.
MA1 DC1 0
DC C A b c a b b
DC b c b c 2,
2
2
b a b a 2,
2
C1 A1 DB a b b a a b 0; DC1 DB b c b a b 1,
1
1 1
2
1
2
2
2
2
1; DB
2
2
2
2

6.

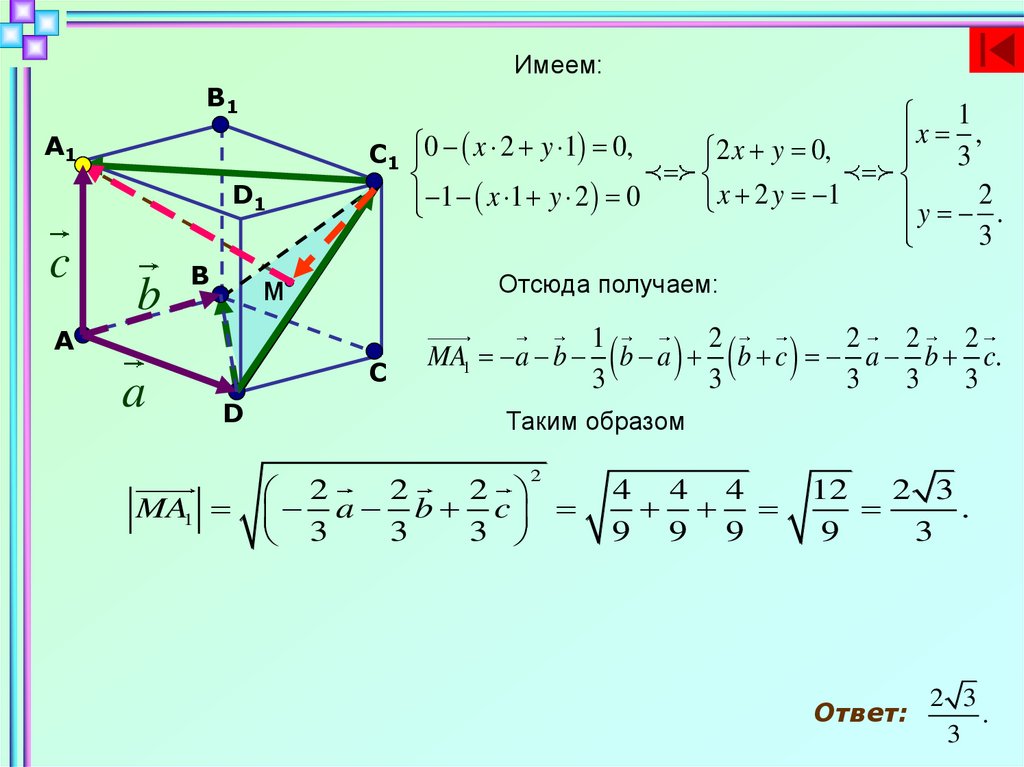
Имеем:
B1
A1
D1
c
b
B
1
x ,
2 x y 0,
C1
0 x 2 y 1 0,
3
x 2 y 1
1 x 1 y 2 0
y 2.
3
Отсюда получаем:
M
A
a
C
D
MA1 a b
Таким образом
2
MA1
1
2
2
2
2
b a b c a b c.
3
3
3
3
3
2
2
2
a
b
c
3
3
3
4 4 4
9 9 9
12
2 3
.
9
3
Ответ:
2 3
.
3

7.

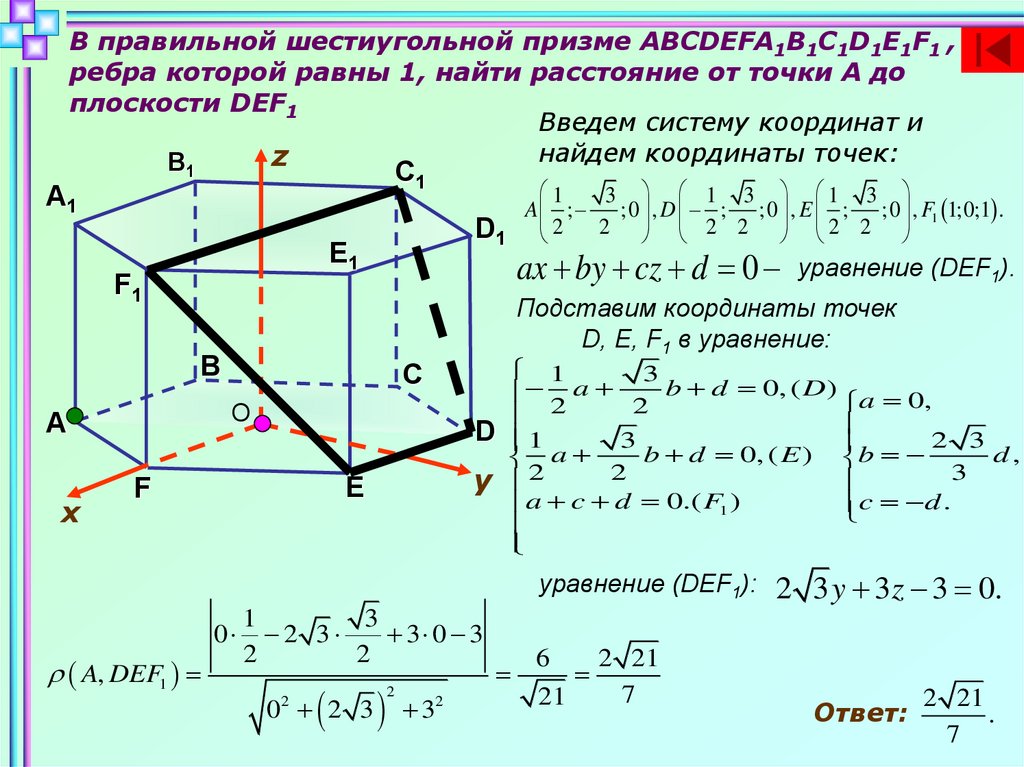
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ,
ребра которой равны 1, найти расстояние от точки А до
плоскости DEF1
Введем систему координат и
найдем координаты точек:
z
B
C1
1
A1
E1
1
3 1 3 1 3
A ; ;0 , D ; ;0 , E ; ;0 , F1 1;0;1 .
D1 2 2 2 2 2 2
ax by cz d 0
F1
Подставим координаты точек
D, E, F1 в уравнение:
B
x
C
O
A
D
y
E
F
1
3
b d 0, ( D )
a
a 0,
2
2
3
2 3
1
b d 0, ( E ) b
d,
a
2
2
3
a c d 0.( F1 )
c d .
уравнение (DEF1):
0
A, DEF1
уравнение (DEF1).
1
3
2 3
3 0 3
2
2
02 2 3
2
32
6
2 21
7
21
2 3 y 3z 3 0.
Ответ:
2 21
.
7

8.

Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние
от точки C до плоскости BDC1
B1
Расстояние х равно высоте CQ, опущенной
C1 в пирамиде BCDC из вершины С на
1
основание BDC1
A1
D1
Q
B
A
1
1 1
a3
V1 S BCD CC1 BC CD CC1 .
3
3 2
6
R
D
Треугольник BDC1 – равносторонний.
C
2
1
1 a 2 3
a2 3
V2 S BC1D CQ
x
x.
3
3
4
6
Так как V1 = V2, то получаем уравнение:
a3
a2 3
a 3
x; x
.
6
6
3
Ответ:
a 3
.
3