Similar presentations:
Метод координат при решении задач по подготовке к ЕГЭ. Координаты многогранников
1.
Метод координатпри решении задач
по подготовке к ЕГЭ
2.
Координатымногогранников.
Учитель ГБОУ Школа № 1897
Шаповалова Е.Д.
3.
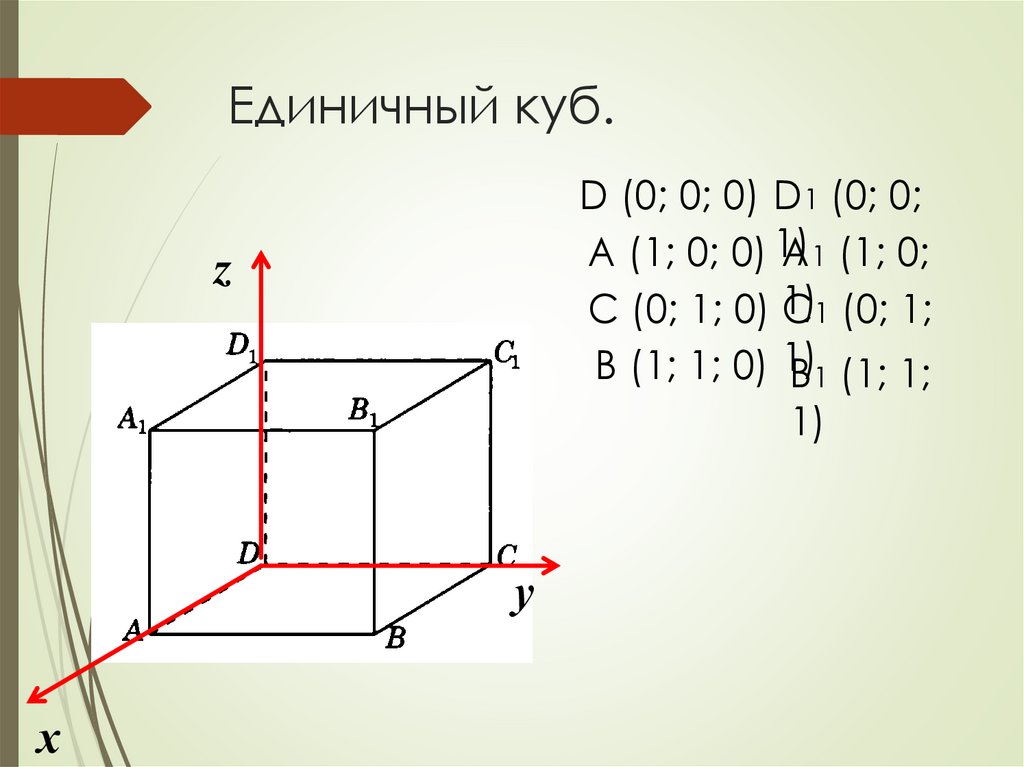
Единичный куб.D (0; 0; 0) D1 (0; 0;
A (1; 0; 0) 1)
A1 (1; 0;
C (0; 1; 0) 1)
C1 (0; 1;
B (1; 1; 0) 1)
B1 (1; 1;
1)
z
у
х
4.
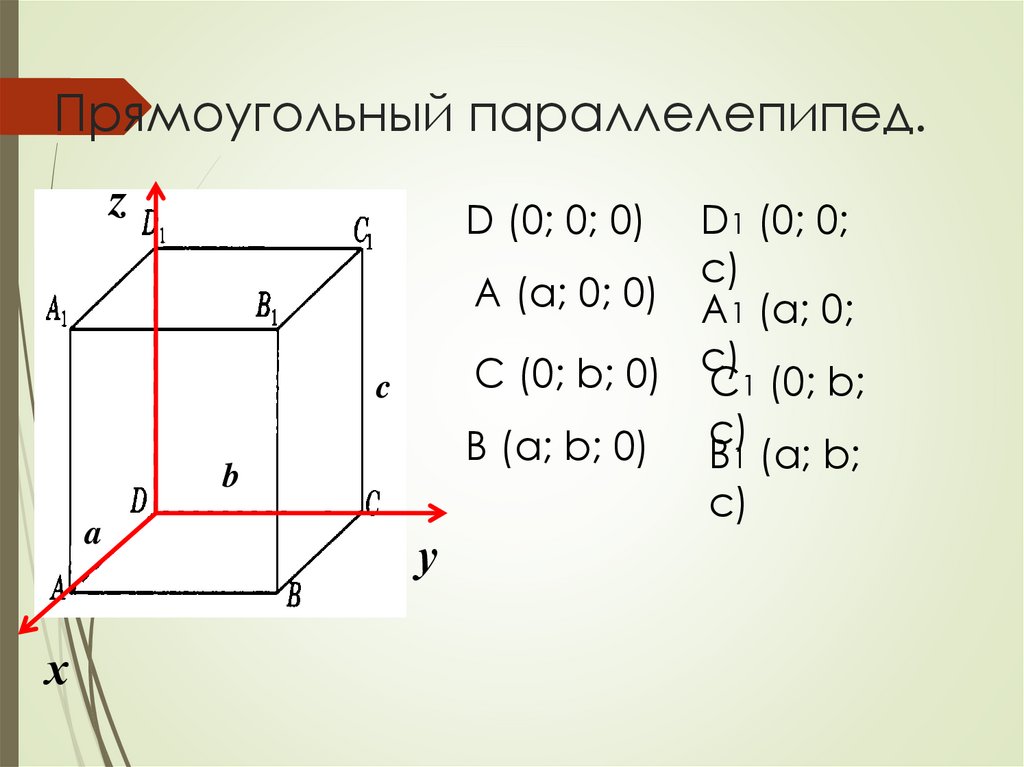
Прямоугольный параллелепипед.z
D (0; 0; 0)
D1 (0; 0;
c)
A (a; 0; 0) A1 (a; 0;
C (0; b; 0) c)
C1 (0; b;
B (a; b; 0) c)
B1 (a; b;
c)
c
b
a
х
у
5.
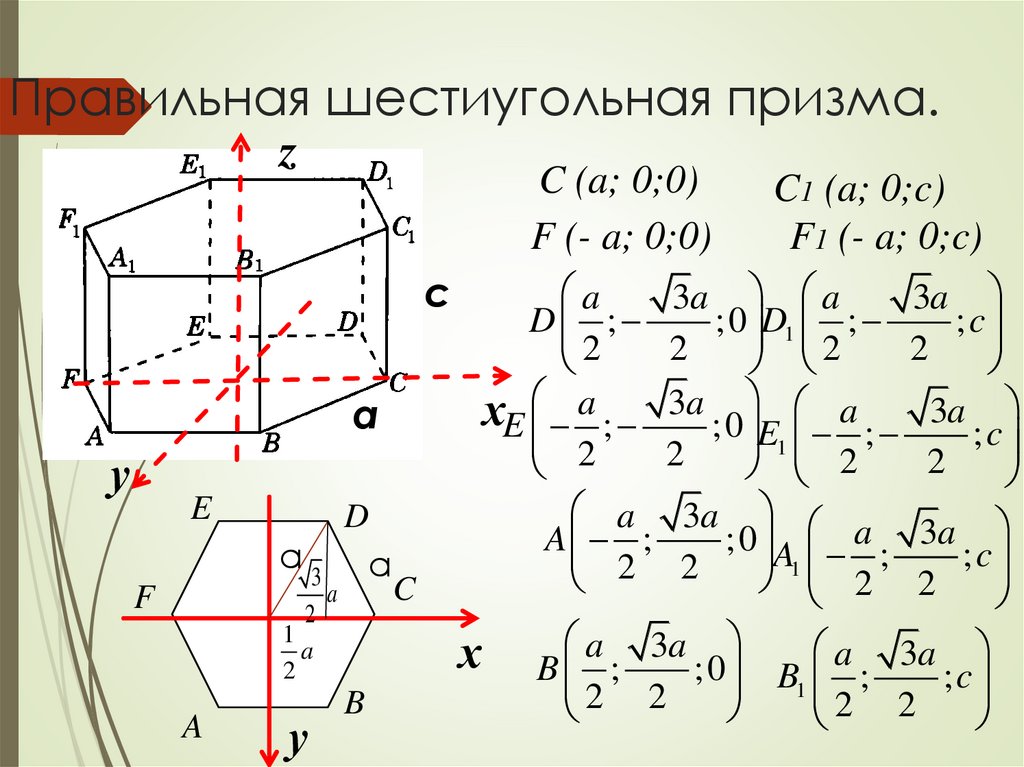
Правильная шестиугольная призма.z
C (a; 0;0)
F (- a; 0;0)
c
a
D ;
2
хE a ;
2
3a a
;0 D1 ;
2
2
3a a
;0 E1 ;
2
2
a 3a
A ;
;0 A a ;
2 2
1 2
a
у
E
a
3
a
2
1
a
2
F
A
у
D
a
C
х
B
C1 (a; 0;c)
F1 (- a; 0;c)
3a
; c
2
3a
; c
2
3a
; c
2
a 3a
a 3a
B ;
;0 B1 ;
; c
2 2
2 2
6.
Правильная треугольная призма.z
С1
3a
B 0;
; 0
2
В1
a
C ;0;0
2
А1
a
2
А
х
a
A ;0;0
2
С
O
c
3a
2
a
В
у
a
A1 ;0; c
2
3a
B1 0;
; c
2
a
C1 ;0; c
2
7.
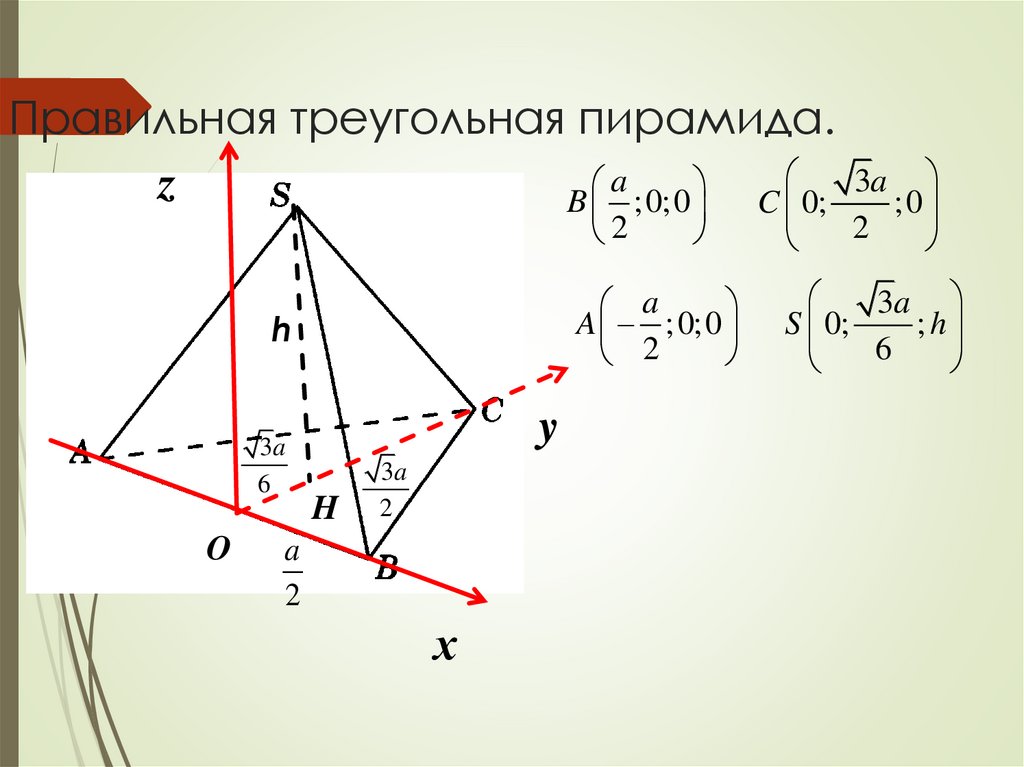
Правильная треугольная пирамида.a
z
B ;0;0
C 0;
2
a
A ;0;0
2
h
3a
6
O
y
H
3a
2
a
2
х
3a
;0
2
3a
S 0;
; h
6
8.
Правильная четырехугольнаяпирамида.
a a
z
a a
A
B ; ;0
; ;0
2
2
a a
C ; ;0
2 2
h
h
х
a a
D ; ;0
2 2
a a
2
y
2
2
S 0;0; h
9.
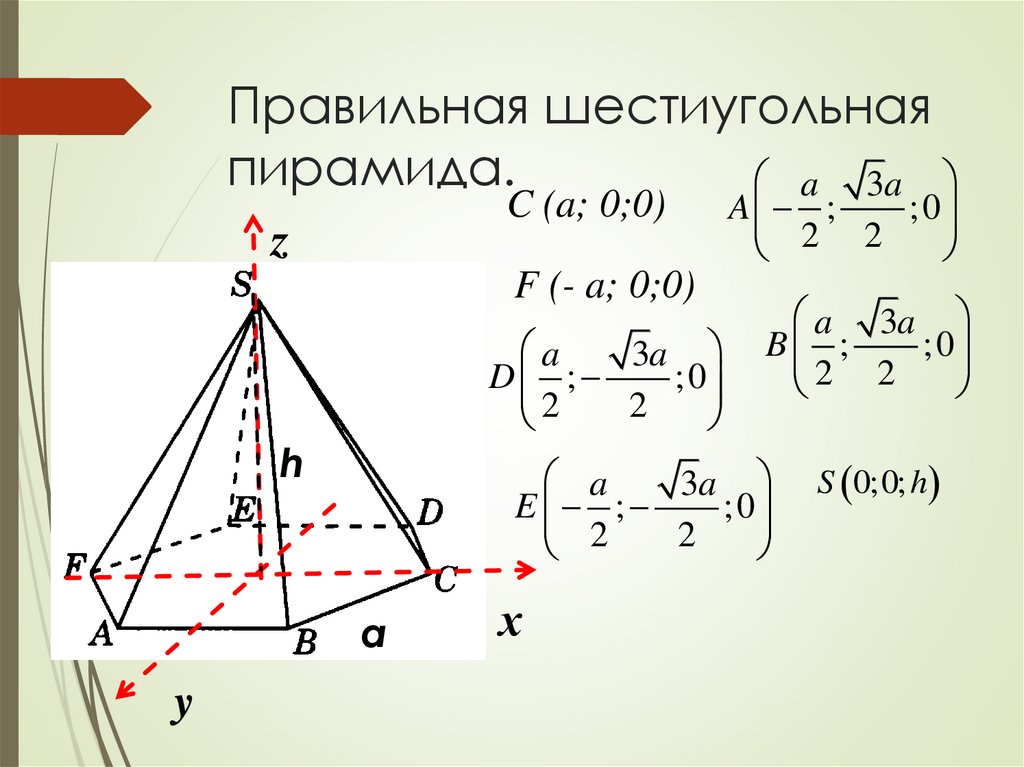
Правильная шестиугольнаяпирамида.
a 3a
C (a; 0;0)
z
F (- a; 0;0)
a
3a
D ;
;0
2
2
h
a 3a
B ;
;0
2 2
a
3a
E ;
;0
2
2
a
y
A ;
;0
2 2
х
S 0;0; h
10.
Расстояние от точкидо плоскости.
11.
Расстояние от точкиМ(x0;y0;z0)до плоскости ax + by
+ cz + d = 0.
M ;
ax0 by0 cz0 d
a b c
2
Например:
M 3;1;2
M ;
2
2
3x 4 y 12 z 2 0
3 3 4 1 12 2 2
3 4 12
2
2
2
27
13
12.
Уравнение плоскости,проходящей через три точки.
M xm ; ym ; zm
N xn ; yn ; zn
P xp ; yp ; z p
Уравнение плоскости имеет вид
ax by cz d 0
Числа a, b, c находим из системы
уравнений
axm bym czm d 0
axn byn czn d 0
ax by cz d 0
p
p
p
13.
Например: Написать уравнение плоскости,проходящей через точки M 0;1;0 N 1;0;0 P 1;1;1
ax by cz d 0
b d 0
a d 0
a b c d 0
a 0 b 1 c 0 d 0
a 1 b 0 c 0 d 0
a 1 b 1 c 1 d 0
b d
a d
d d c d 0
b d
a d
c d
dx dy dz d 0 : d
- уравнение плоскости, проходящей
x y z 1 0 через три данные точки.
14.
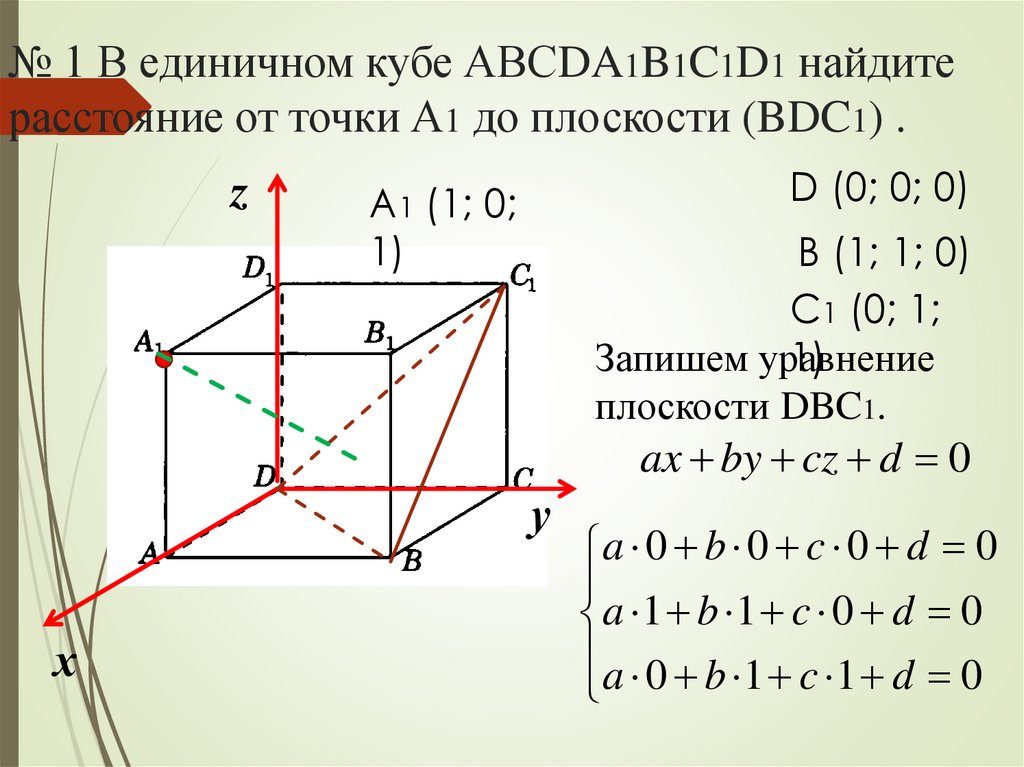
№ 1 В единичном кубе АВСDA1B1C1D1 найдитерасстояние от точки А1 до плоскости (BDC1) .
z
D (0; 0; 0)
A1 (1; 0;
1)
B (1; 1; 0)
C1 (0; 1;
1)
Запишем уравнение
плоскости DBC1.
ax by cz d 0
у
х
a 0 b 0 c 0 d 0
a 1 b 1 c 0 d 0
a 0 b 1 c 1 d 0
15.
d 0a b d 0
b c d 0
d 0
a b
c b
Найдем искомое
расстояние по формуле
bx by bz 0 : b
x y z 0
M ;
A1 (1; 0;
1)
ax0 by0 cz0 d
1 1 1 0 1 1
a b c
2
2
2
2
2 3
A1 ;( BC1 D)
2
2
2
3
3
1 ( 1) 1
2 3
Ответ:
3
16.
№ 2. В правильной шестиугольнойпризме все ребра равны 1.
C1 (1;
0;1)
Найдите расстояние
от
точки
А
до
1 3
z
A 1);
;0
плоскости (DEF
2 2
1
у
1
х
1
3
D ;
;0
2
2
F1 (- 1; 0;1)
Запишем уравнение
плоскости DC1F1.
ax by cz d 0
17.
a 1 b 0 c 1 d 0a c d 0
3
1
3
1
b d 0
a
c 0 d 0
a b
2
2
2
2
a c d 0
a 1 b 0 c 1 d 0
a 0
2
0
x
dy
dz
d
0
:d
c
d
3
2
b
d
2
3
y z 1 0
3
18.
Найдем искомоерасстояние по формуле
M ;
2
0 x
y z 1 0
3
A; DC1 F1
a 2 b2 c 2
1 3
A ;
;0
2 2
3
1 2
0
1 0 1
3 2
2
2
2
2
0
1
3
2
2 3
Ответ:
7
ax0 by0 cz0 d
2 3
7
19.
Расстояние междускрещивающимися
прямыми.
20.
Расстоянием между скрещивающимися прямыминазывается расстояние между одной из
скрещивающихся прямых и плоскостью, проходящей
через вторую прямую, параллельно первой.
b
b; c b; A;
A
B
b
c
21.
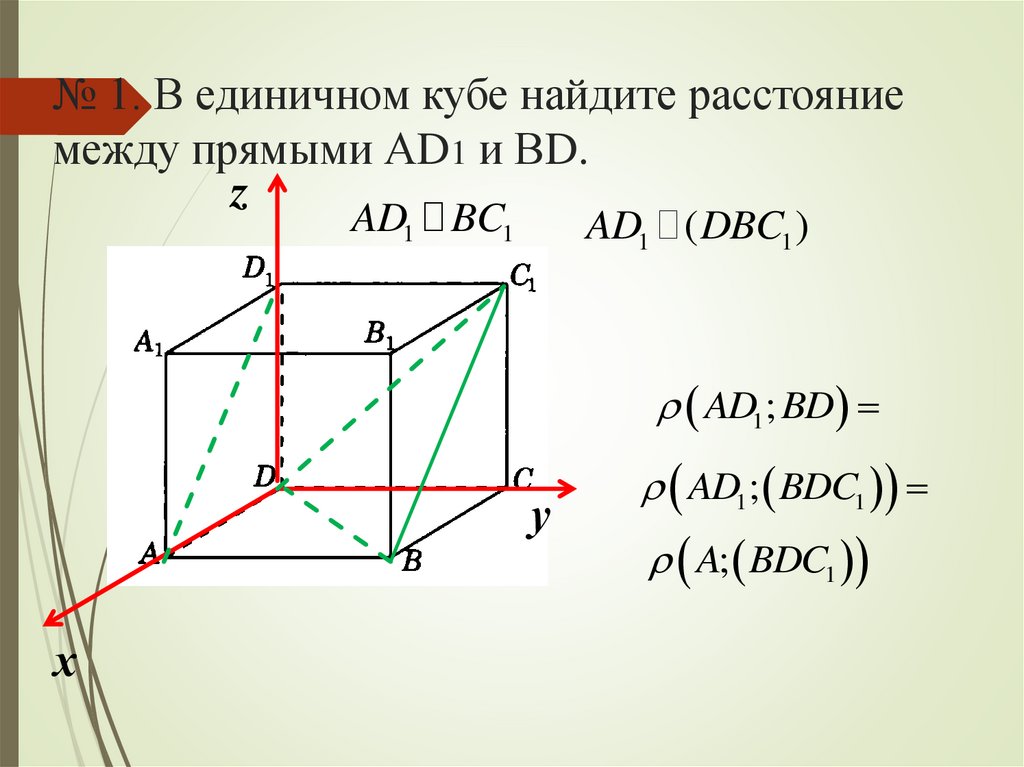
№ 1. В единичном кубе найдите расстояниемежду прямыми АD1 и ВD.
z
AD1 BC1
AD1 ( DBC1 )
AD1; BD
у
х
AD1; BDC1
A; BDC1
22.
D (0; 0; 0) Запишем уравнениеB (1; 1; 0) плоскости BDC1.
C1 (0; 1;
ax by cz d 0
1)0
a
0
b
0
c
0
d
d 0
A (1; 0; 0)
a 1 b 1 c 0 d 0
a 0 b 1 c 1 d 0
a b
c b
bx by bz 0
x y z 0
M ;
Найдем искомое
расстояние по формуле
ax0 by0 cz0 d
a b c
2
2
2
23.
A (1; 0; 0)x y z 0
1 1 1 0 1 0
1
3
A;( BC1 D)
3
3
12 ( 1) 2 12
3
Ответ:
3
24.
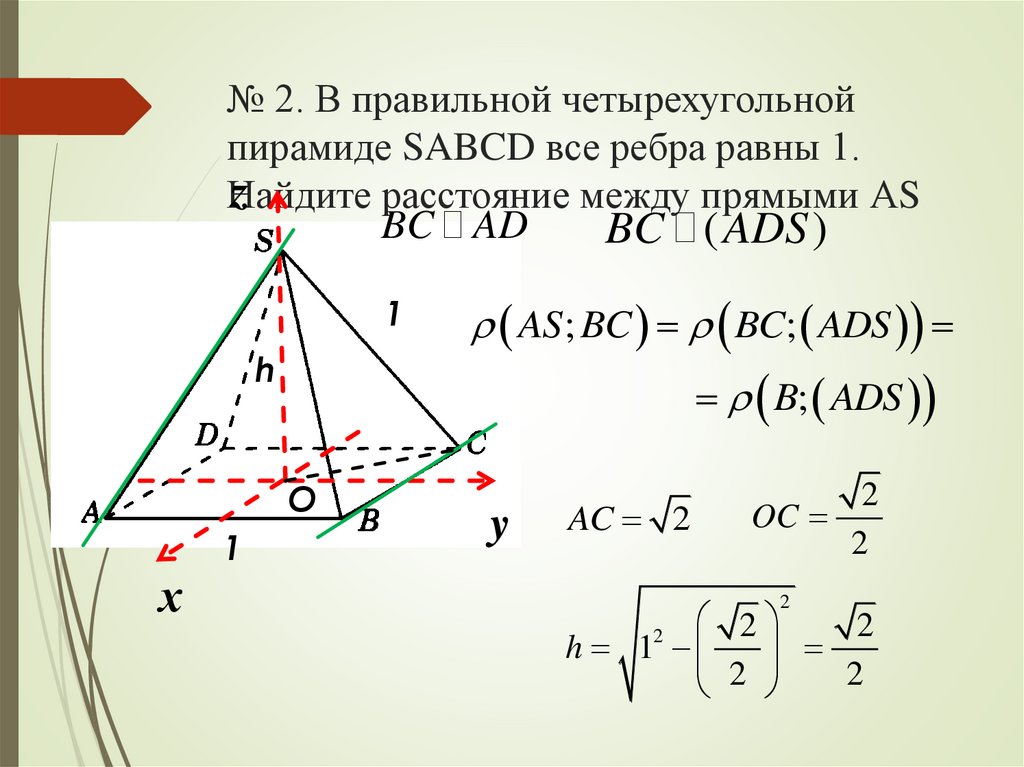
№ 2. В правильной четырехугольнойпирамиде SABCD все ребра равны 1.
z
Найдите
расстояние между прямыми АS
BC ( ADS )
и ВС. BC AD
1
h
B; ADS
O
1
х
AS ; BC BC; ADS
y
AC 2
2
OC
2
2
2
2
h 1
2
2
2
25.
1 1B ; ;0
2 2
1 1
A ; ;0 S 0;0; 2
2 2
2
1 1
Запишем
D ; ;0
2 2
1
1
a b c 0 d 0
2
2
1
1
a b c 0 d 0
2
2
2
a 0 b 0 c
d 0
2
уравнение
плоскости ADS.
1
1
2 a 2 b d 0
1
1
a b d 0
2
2
2
c d 0
2
26.
a 0b 2d
c 2 d
0 x 2dy 2dz d 0 : d
0 x 2 y 2z 1 0
Найдем искомое
расстояние по формуле
1 1
B ; ;0
2 2
B;( ASD)
M ;
a 2 b2 c 2
1
1
0 2 2 0 1
2
2
0 2 2
2
Ответ: 6
3
ax0 by0 cz0 d
2
2
2
6
3
6
27.
Литература :Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и
методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые
задания С2) 18.02.2011
www.alexlarin.narod.ru










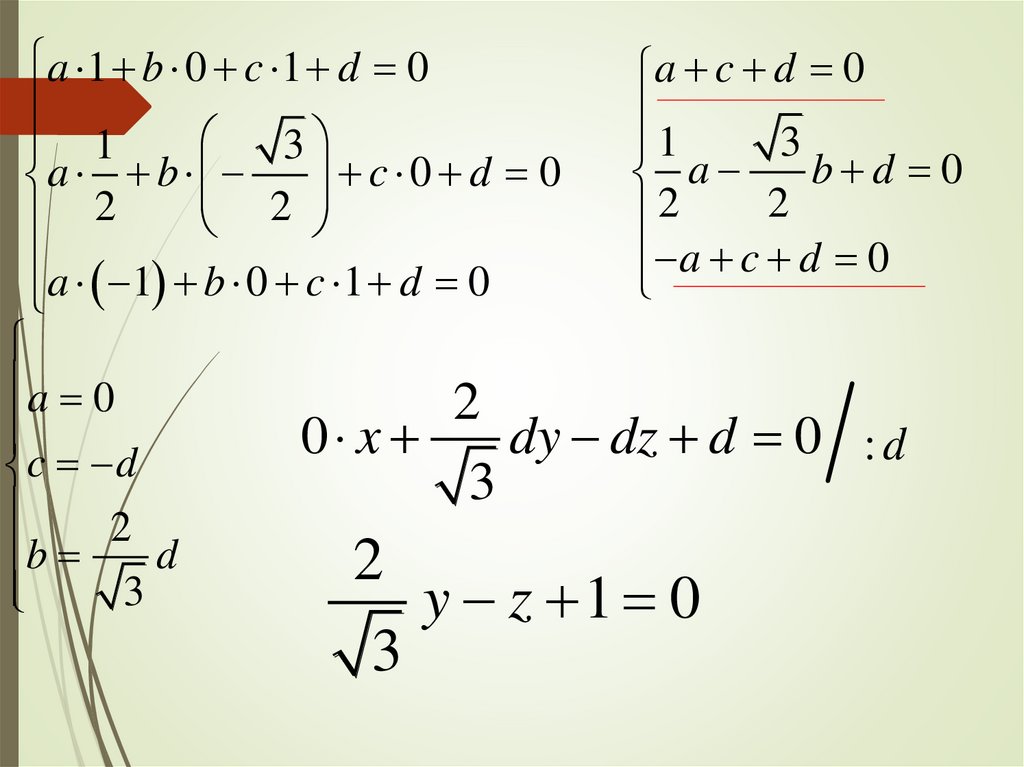








 mathematics
mathematics








