Функция у=arccos x

1.

2.

y
y = cos x
2
3
2
2
1
0
-1
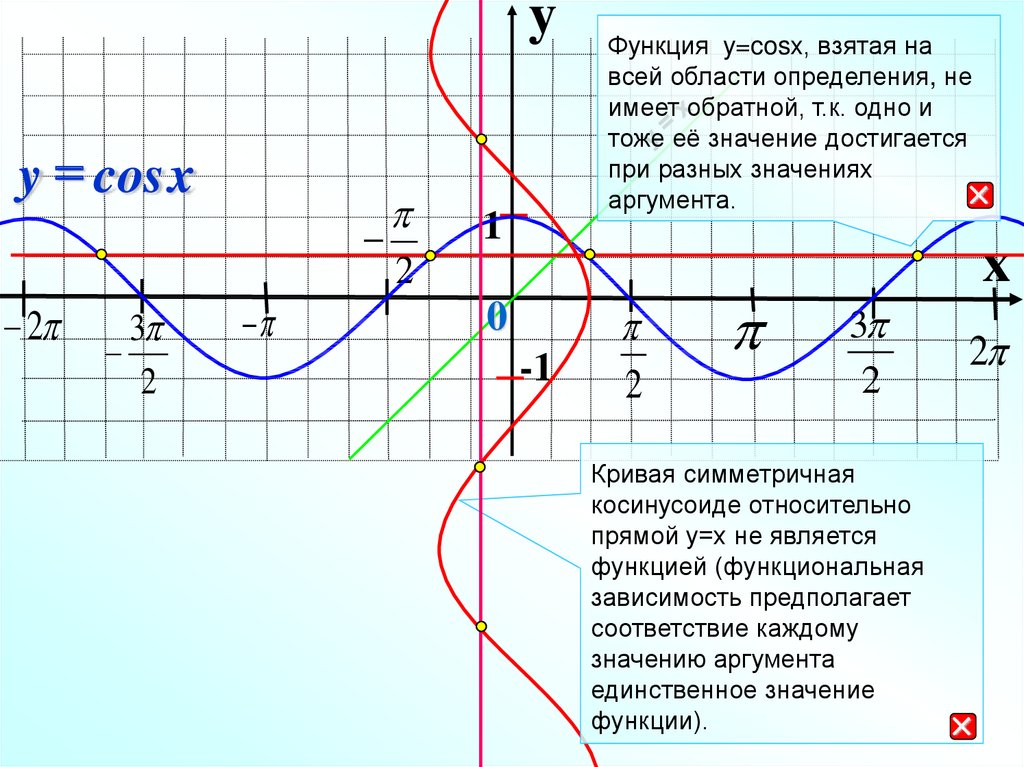
Функция y=cosx, взятая на
всей области определения, не
имеет обратной, т.к. одно и
тоже её значение достигается
при разных значениях
аргумента.
2
x
3
2
Кривая симметричная
косинусоиде относительно
прямой у=х не является
функцией (функциональная
зависимость предполагает
соответствие каждому
значению аргумента
единственное значение
функции).
2

3.

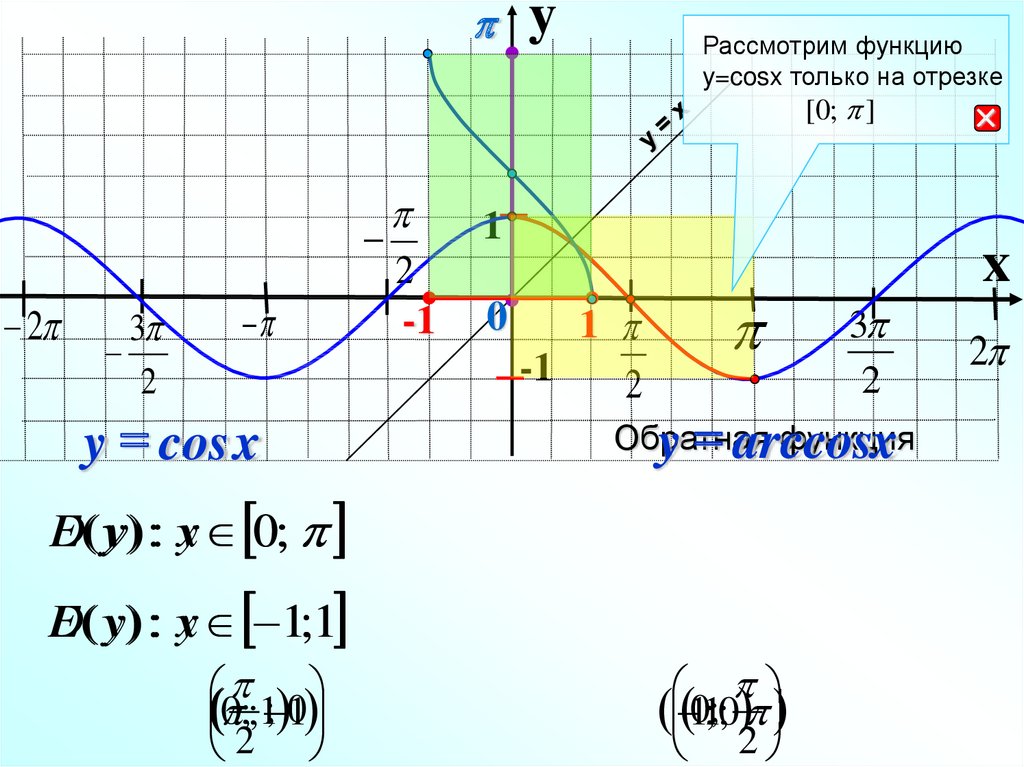
y
Рассмотрим функцию
y=cosx только на отрезке
[0; ]
2
2
3
2
y = cos x
-1
1
0
1
-1
2
D
E( y) : yx 1;1
; 1
0
0;;1
2
x
3
2
Обратная
функция
y = arccos
x
D
E( у) : yх 0;
101;;;0
2
2

4.

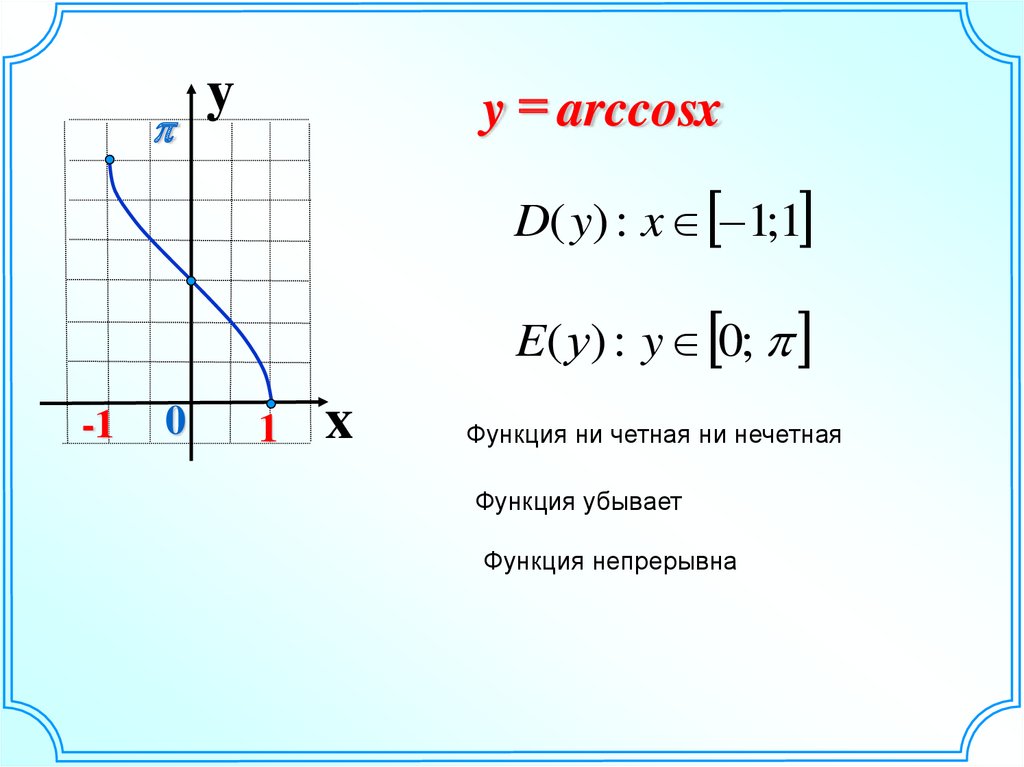
y = arccosx
y
D( y) : x 1;1
E( у) : y 0;
-1
0
1
x
Функция ни четная ни нечетная
Функция убывает
Функция непрерывна

5.

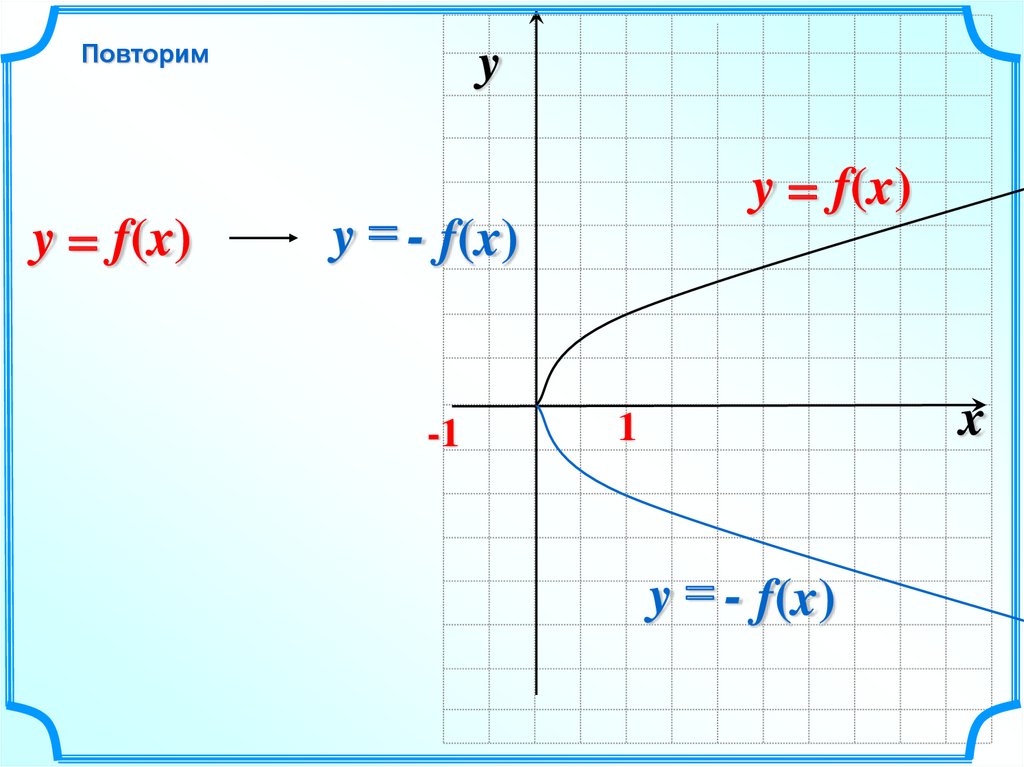
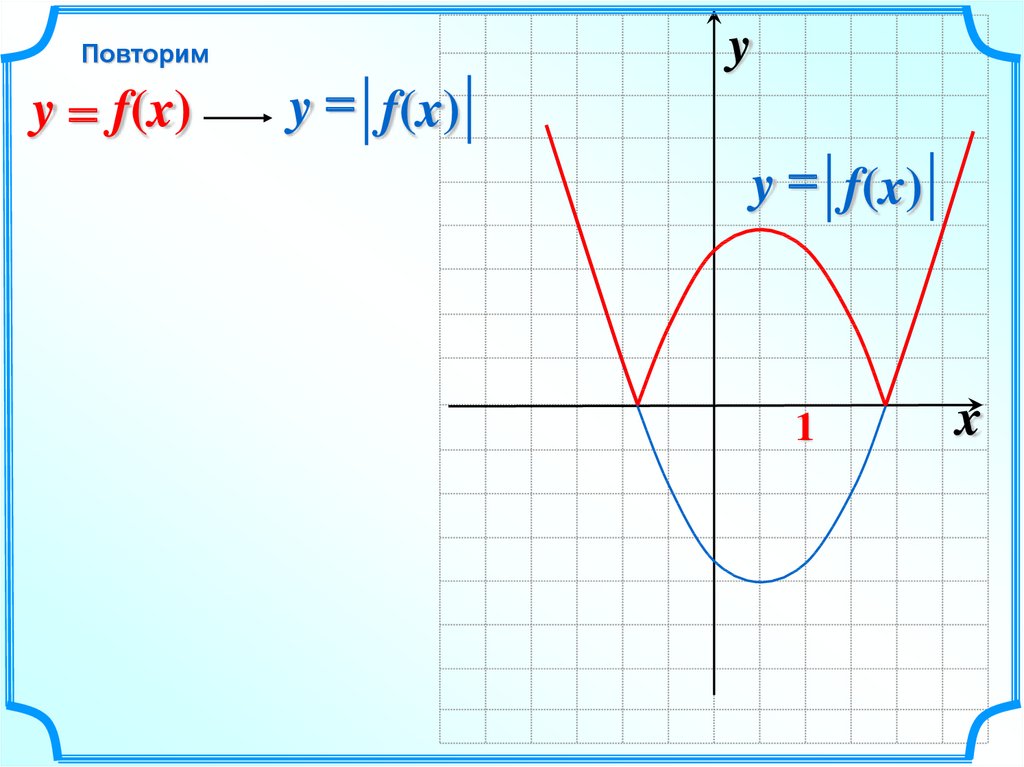
Повторим
y = f(x)
y
y = f(x)
y = - f(x)
-1
x
1
y = - f(x)

6.

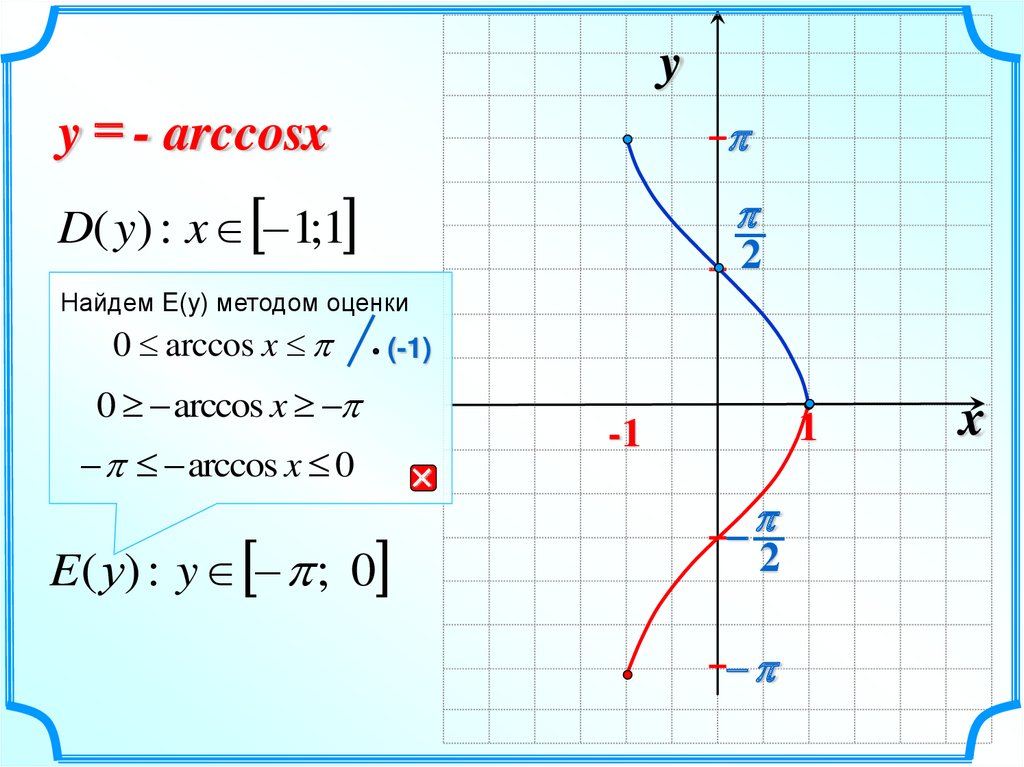
y
y = - arccosx
D( y) : x 1;1
2
Найдем E(y) методом оценки
0 arccos x
(-1)
0 arccos x
arccos x 0
E( у) : y ; 0
1
-1
2
x

7.

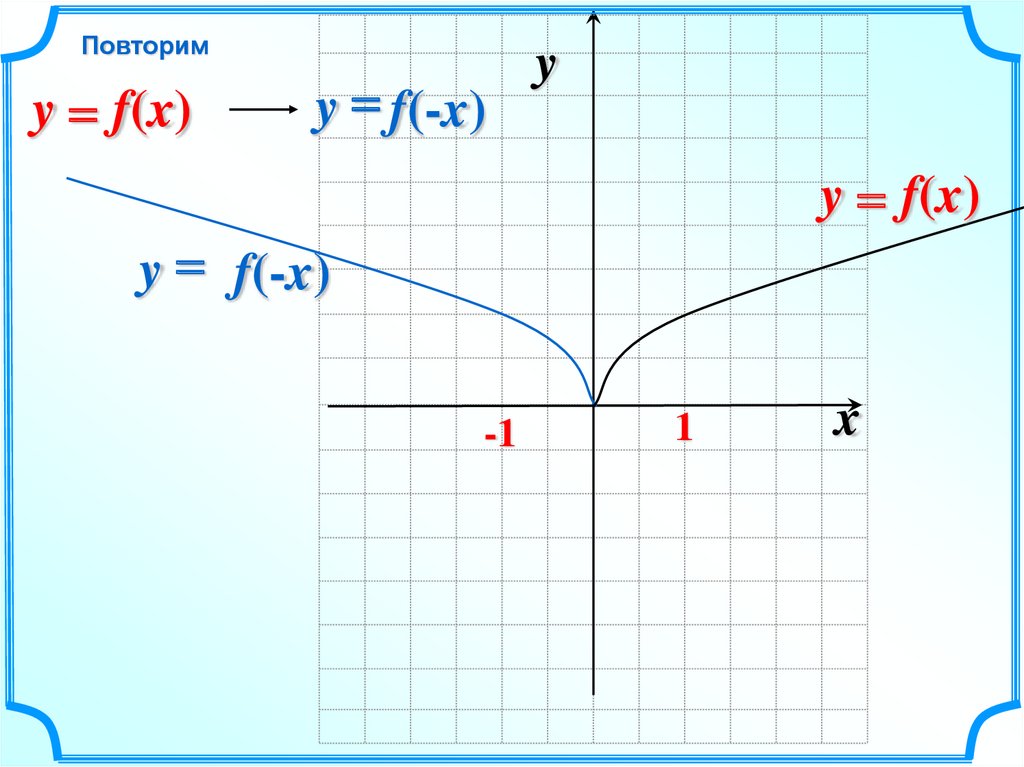
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x

8.

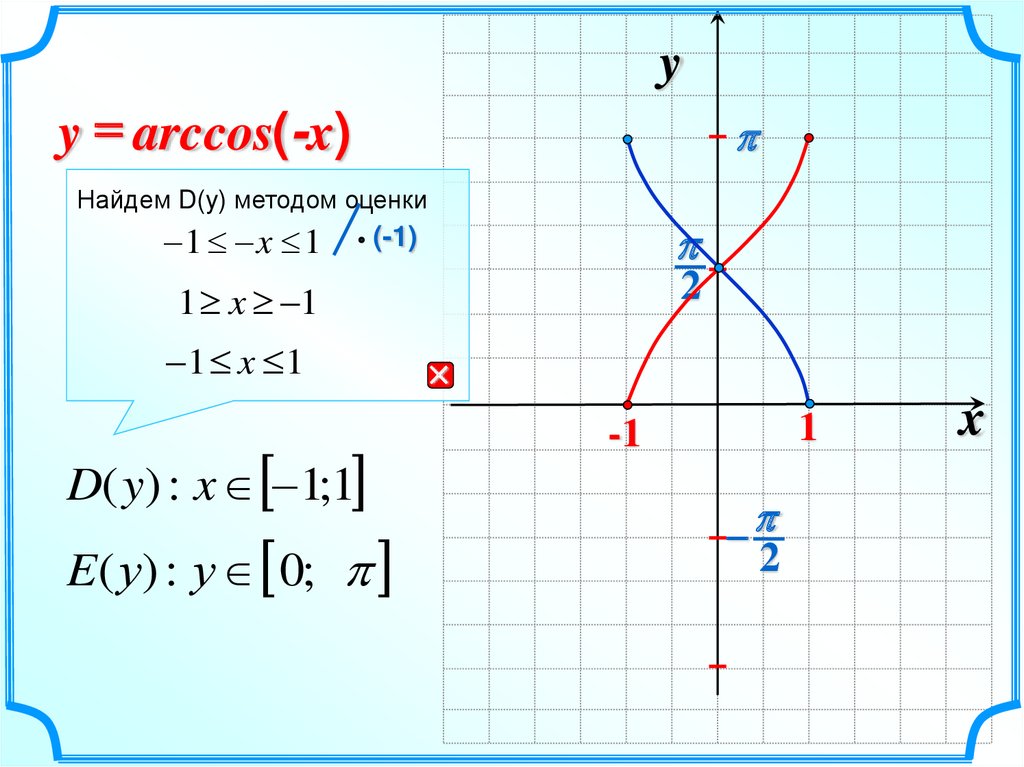
y
y = arccos(-x)
Найдем D(y) методом оценки
1 x 1
(-1)
2
1 x 1
1 x 1
D( y) : x 1;1
E( у) : у 0;
1
-1
2
x

9.

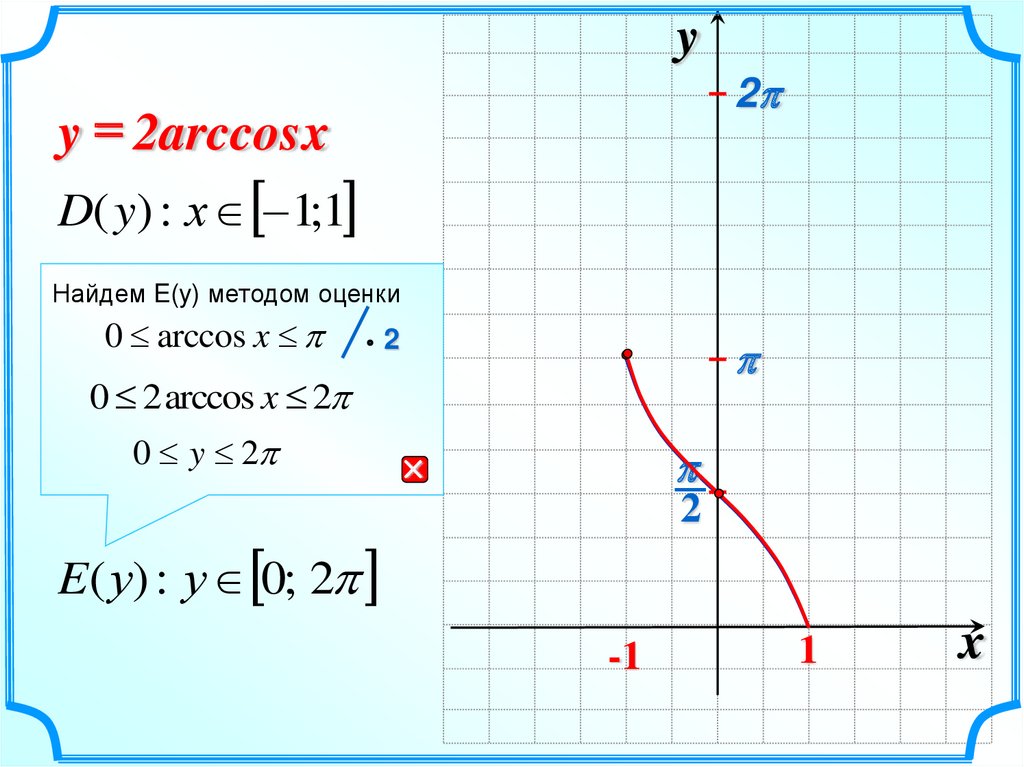
y
y = 2arccos x
2
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
2
0 2 arccos x 2
0 y 2
2
E( у) : у 0; 2
-1
1
x

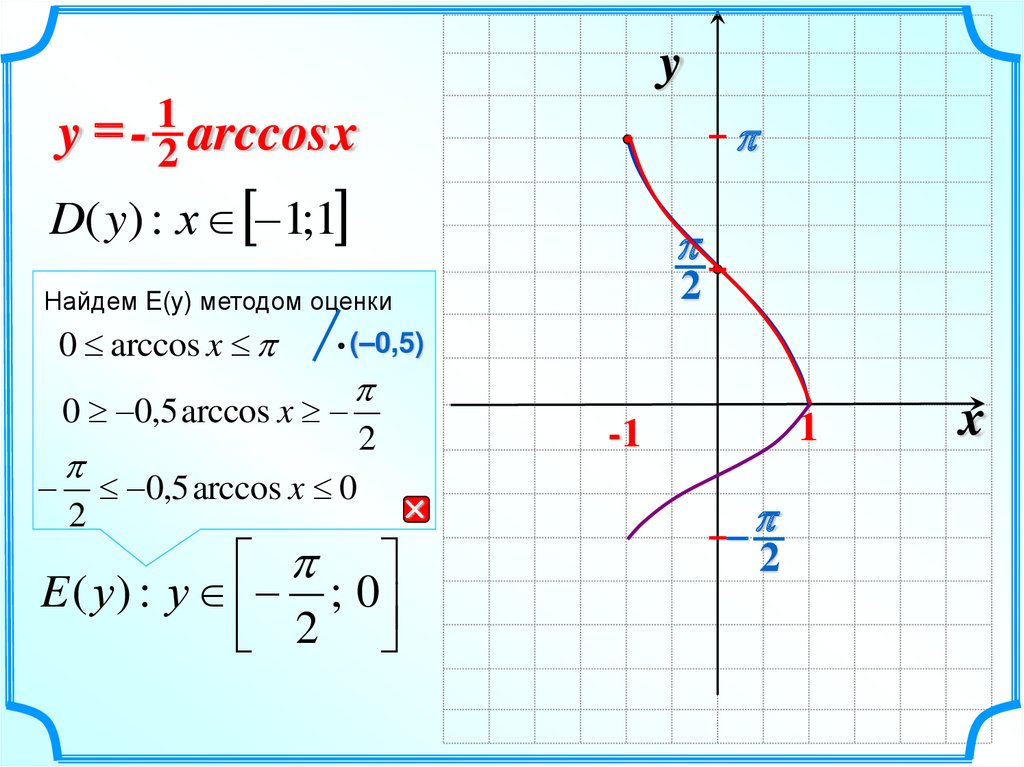
10.

y
1
=
y - 2 arccos x
D( y) : х 1;1
2
Найдем E(y) методом оценки
0 arccos x
0 0,5 arccos x
2
(–0,5)
0,5 arccos x 0
E ( у ) : у ; 0
2
1
-1
2
2
x

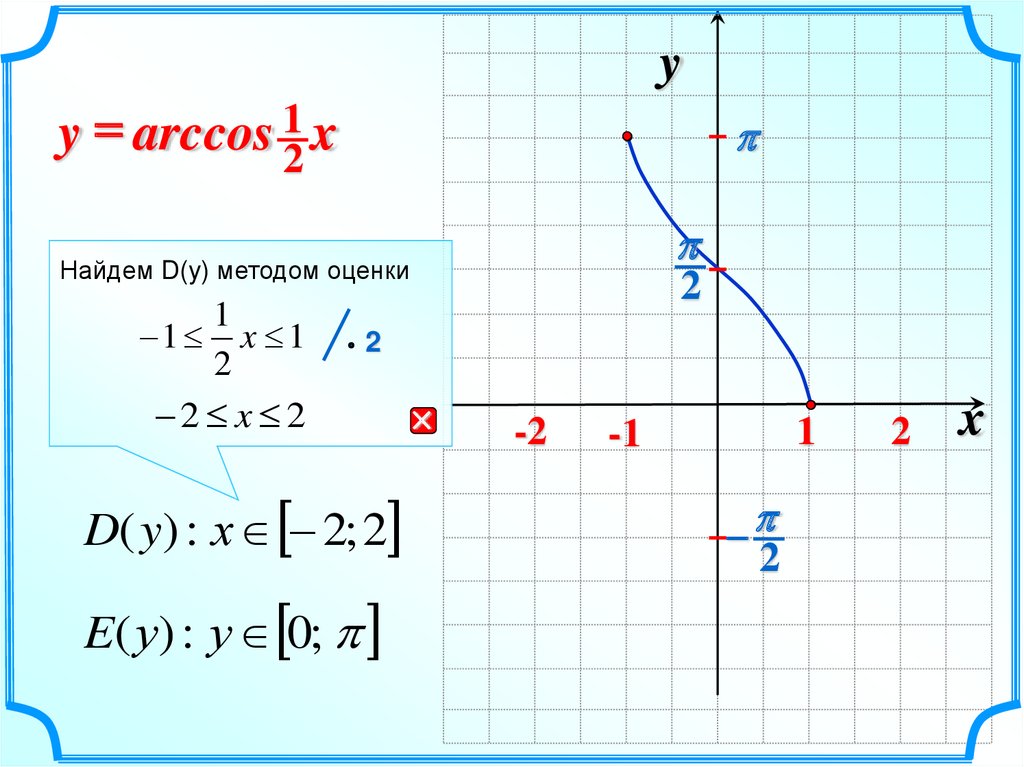
11.

y
y = arccos 12 x
Найдем D(y) методом оценки
1
1 x 1
2
2 x 2
2
2
D( y) : х 2; 2
E( у) : у 0;
-2
1
-1
2
2
x

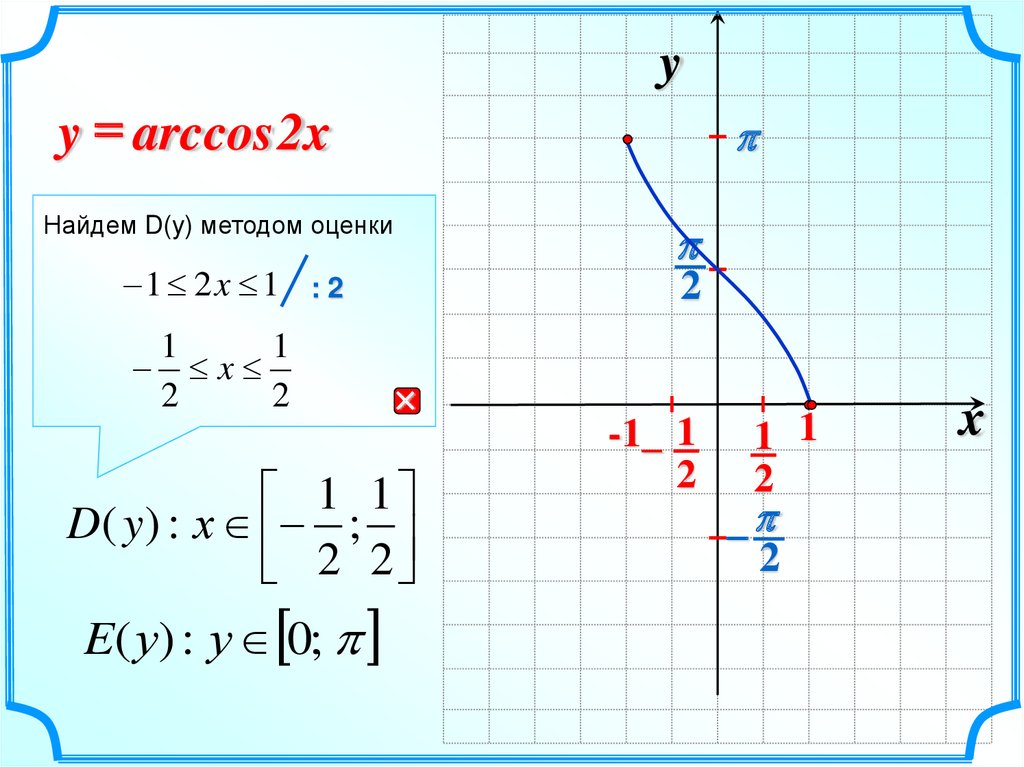
12.

y
y = arccos 2x
Найдем D(y) методом оценки
1 2x 1 : 2
1
1
x
2
2
2
1 1
D( y ) : х ;
2 2
E( у) : у 0;
-1– 1
2
1 1
2
2
x

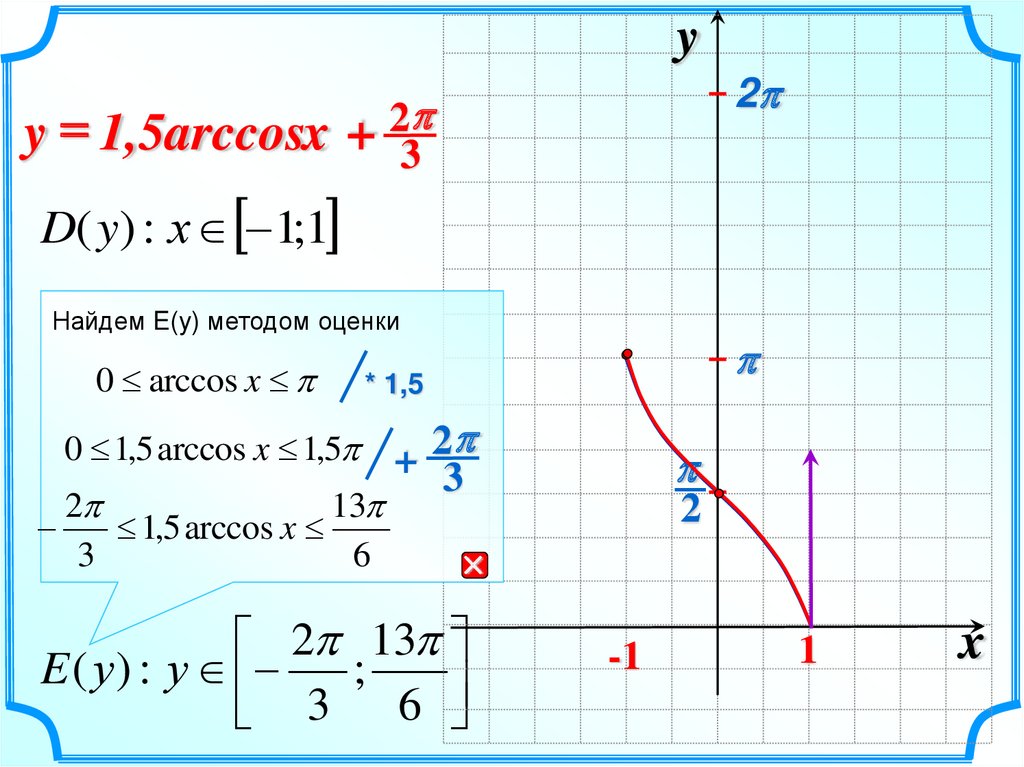
13.

y
y = 1,5arccosx +
2
2
3
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
* 1,5
0 1,5 arccos x 1,5 + 2
3
2
13
1,5 arccos x
3
6
2 13
E ( у ) : у
;
3
6
2
-1
1
x

14.

Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x

15.

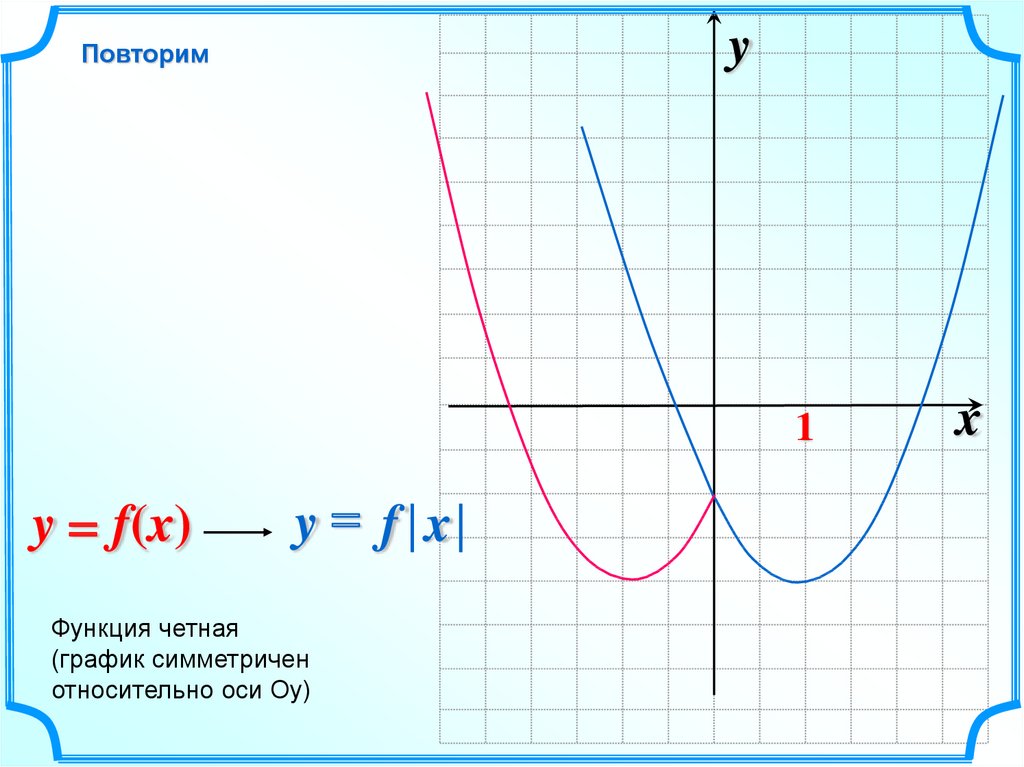
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x

16.

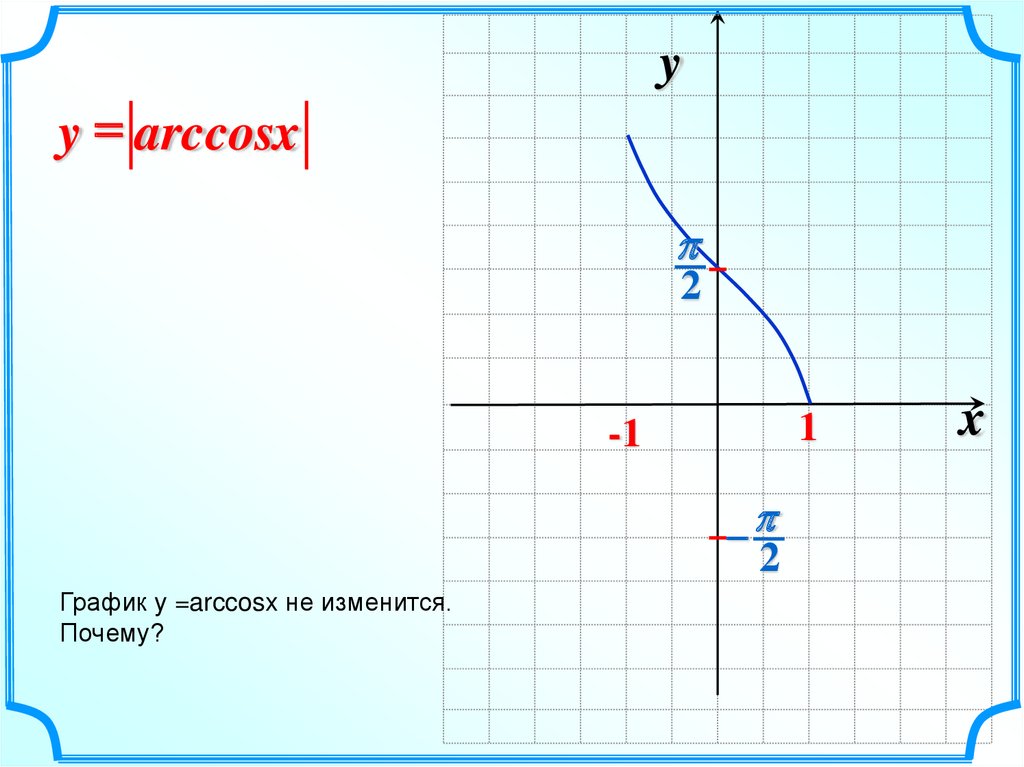
y
y = arccosx
2
1
-1
2
График y =arccosx не изменится.
Почему?
x

17.

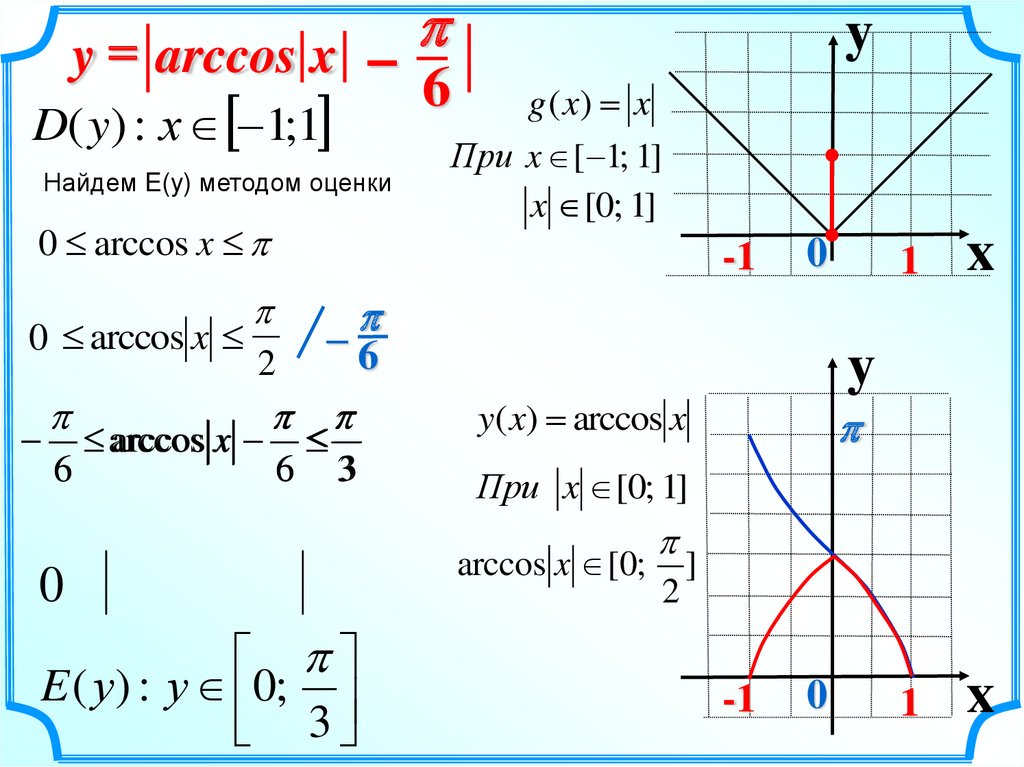
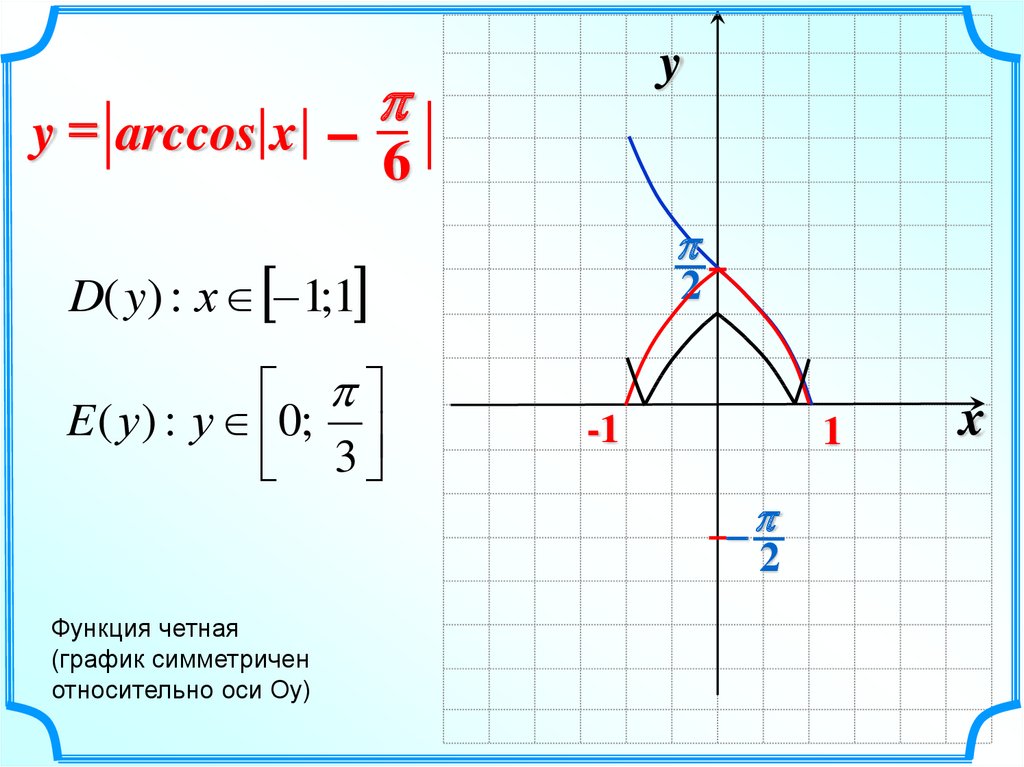
y = arccos x –
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
0 arccos x
–6
2
arccos x
6 3
6
0
E ( у ) : у 0;
3
y
6
g ( x) = x
При x [ 1; 1]
x [0; 1]
-1
0
1
x
1
x
y
y( x) = arccos x
При x [0; 1]
arccos x [0;
2
]
-1
0

18.

y = arccos x –
y
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
-1
1
2
x

19.

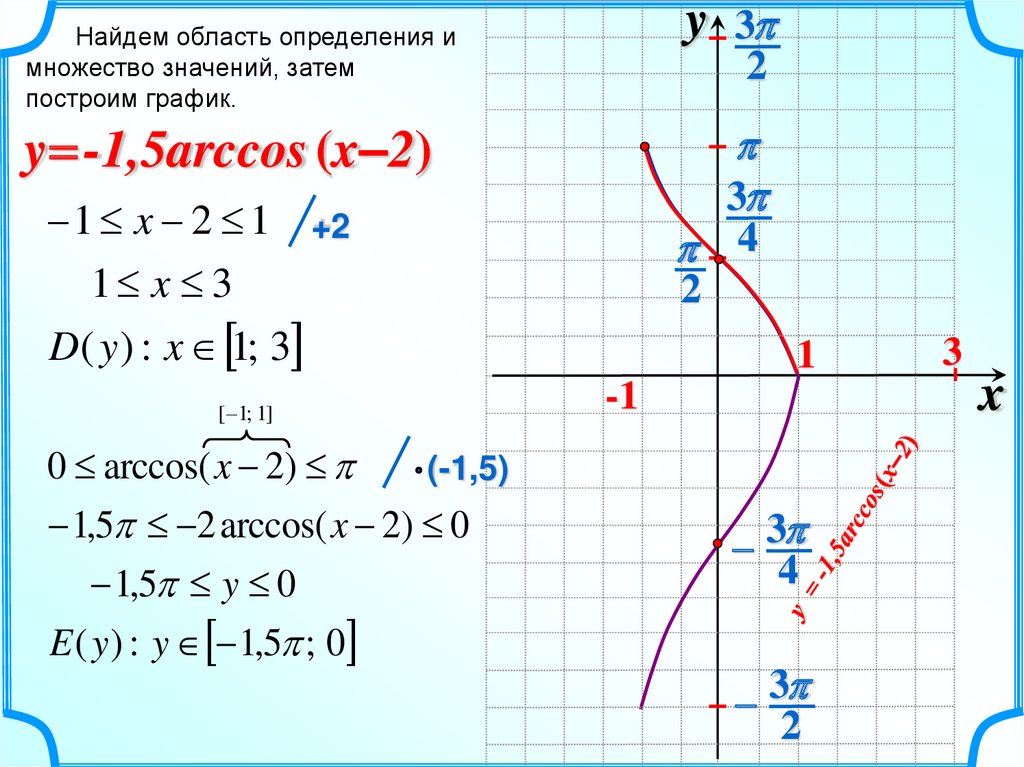
y 3
Найдем область определения и
множество значений, затем
построим график.
2
y = -1,5arccos (x–2)
3
1 x 2 1 +2
1 x 3
D( y ) : x 1; 3
[ 1; 1]
0 arccos( x 2)
(-1,5)
1,5 2 arccos( x 2) 0
1,5 y 0
E ( y ) : y 1,5 ; 0
4
2
1
-1
3
4
3
2
3
x

20.

3
y = arccos( x – )
4
D( y )
3
1 х 1
4
+3
4
1
3
х 1
4
4
3
х 1
4
3
3
1 х 1
4
4
3 3
D ( y ) : х 1 ;1
4 4

21.

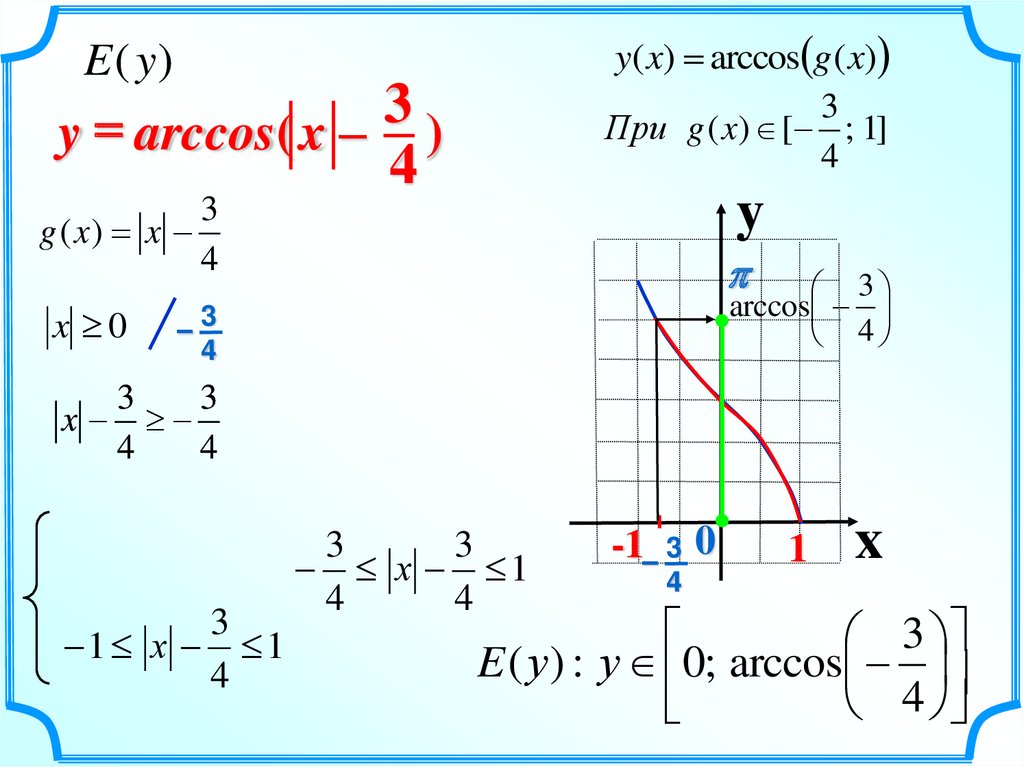
y( x) = arccos g ( x)
3
При g ( x) [ ; 1]
4
E ( y)
3
y = arccos( x – )
4
y
3
g ( x) = x
4
x 0
3
arccos
4
–3
4
3
3
x
4
4
3
1 х 1
4
3
3
х 1
4
4
-1– 3 0
1
x
4
3
E ( у ) : у 0; arccos
4

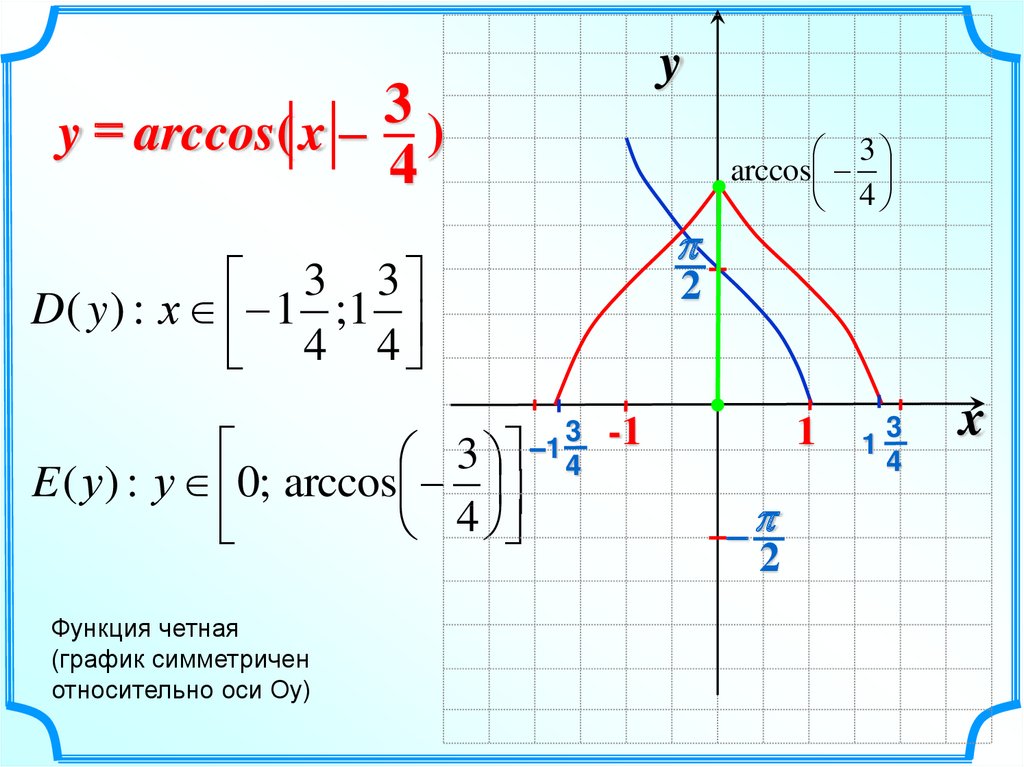
22.

y
3
y = arccos( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
2
3
–1
3 4
E ( у ) : у 0; arccos
4
Функция четная
(график симметричен
относительно оси Оу)
3
arccos
4
-1
1
2
1
3
4
x