Комплексный чертеж отрезка прямой

1.

И.Ю. Амирджанова
«НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ»
Слайдовый лекционный курс
Лекция 2

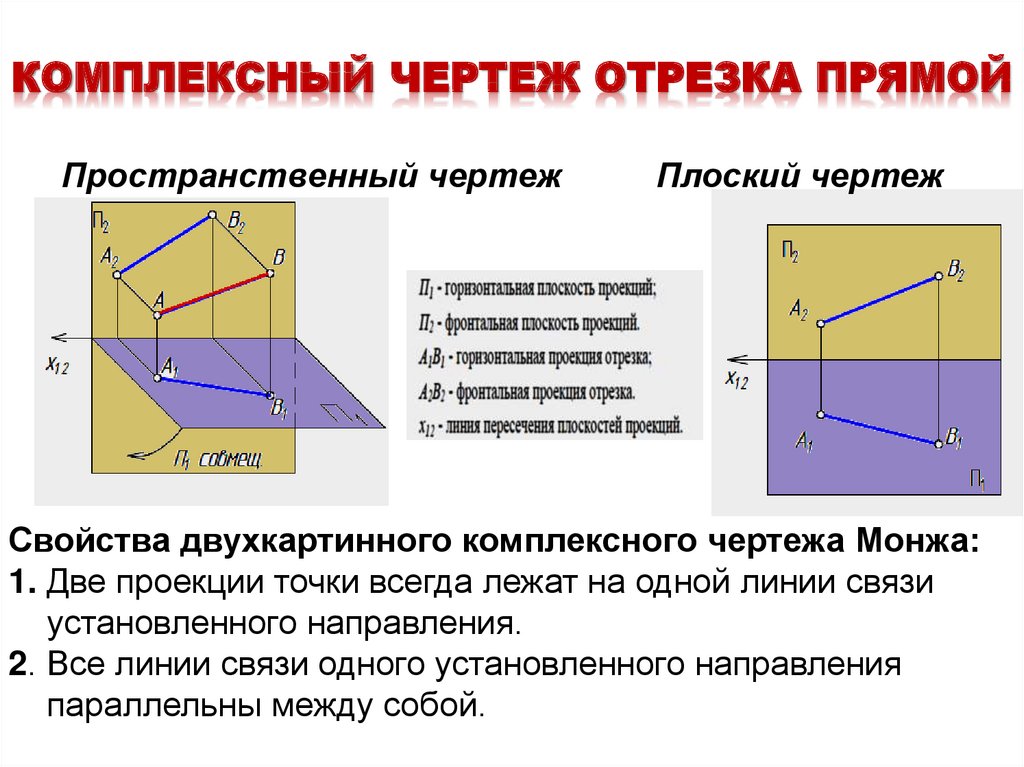
2. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ОТРЕЗКА ПРЯМОЙ

Пространственный чертеж
Плоский чертеж
Свойства двухкартинного комплексного чертежа Монжа:
1. Две проекции точки всегда лежат на одной линии связи
установленного направления.
2. Все линии связи одного установленного направления
параллельны между собой.

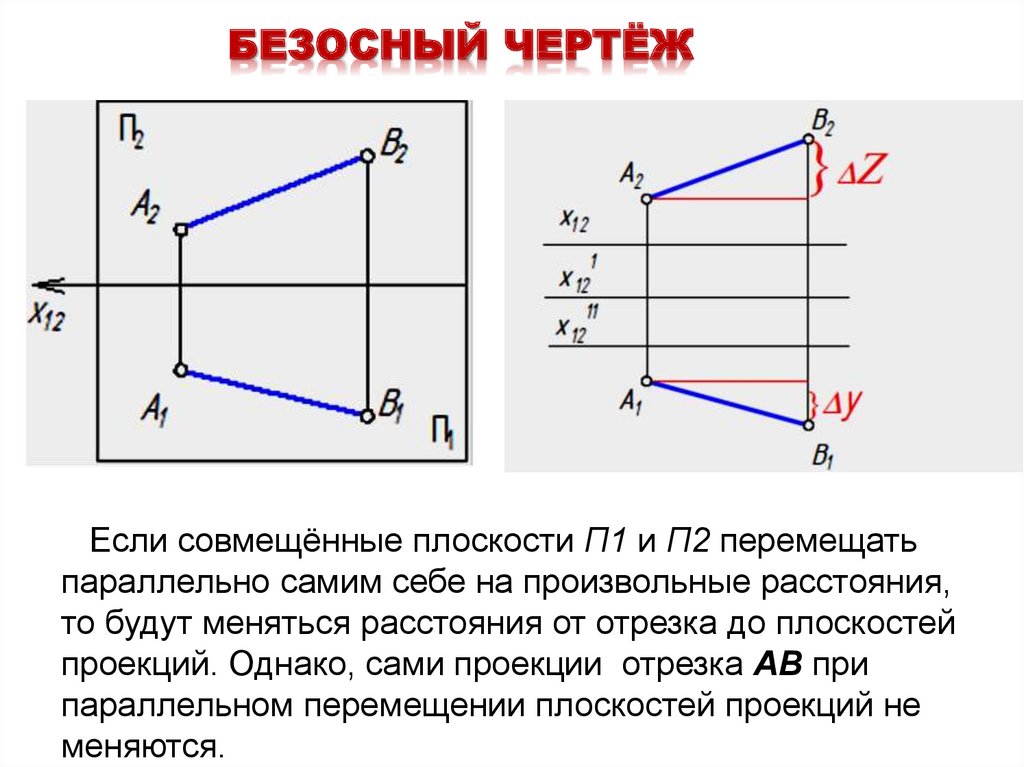
3. БЕЗОСНЫЙ ЧЕРТЁЖ

Если совмещённые плоскости П1 и П2 перемещать
параллельно самим себе на произвольные расстояния,
то будут меняться расстояния от отрезка до плоскостей
проекций. Однако, сами проекции отрезка АВ при
параллельном перемещении плоскостей проекций не
меняются.

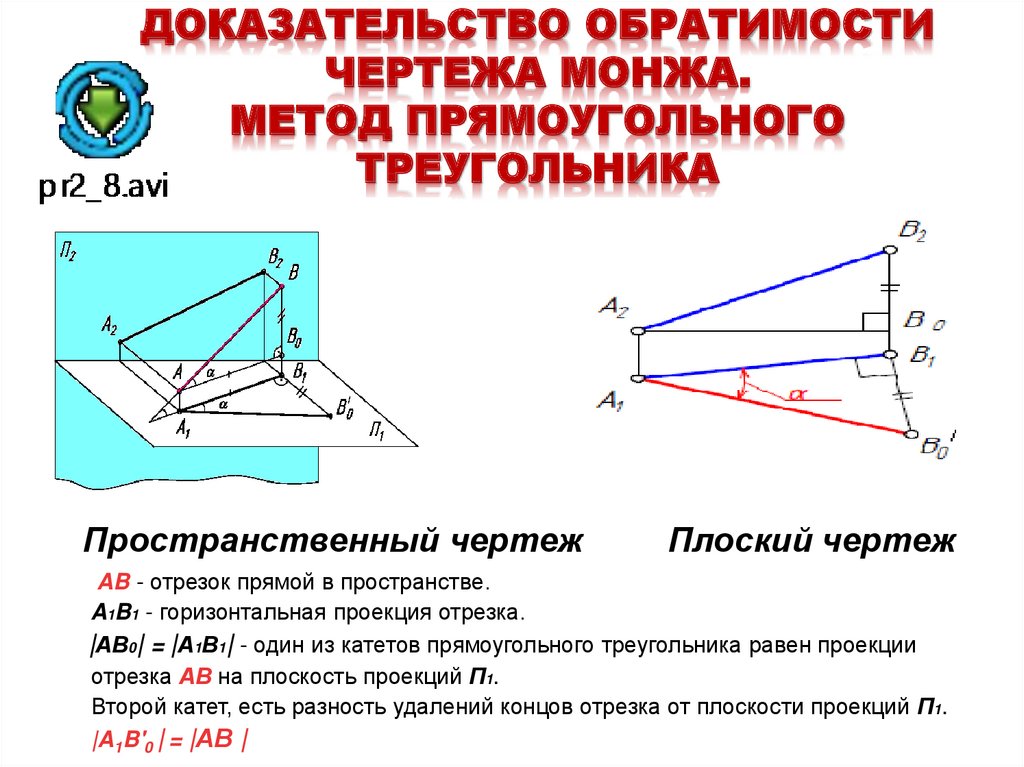
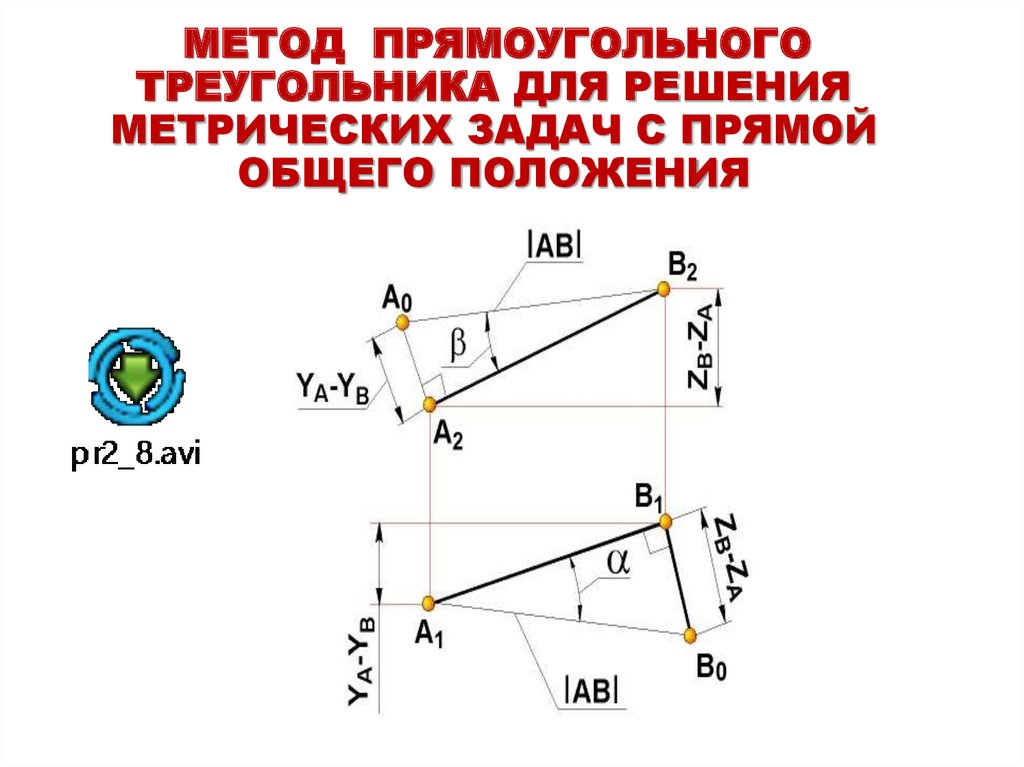
4. ДОКАЗАТЕЛЬСТВО ОБРАТИМОСТИ ЧЕРТЕЖА МОНЖА. МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

Пространственный чертеж
Плоский чертеж
AB - отрезок прямой в пространстве.
A1B1 - горизонтальная проекция отрезка.
|АВ0| = |А1В1| - один из катетов прямоугольного треугольника равен проекции
отрезка АВ на плоскость проекций П1.
Второй катет, есть разность удалений концов отрезка от плоскости проекций П1.
|A1B'0 | = |АВ |

5.

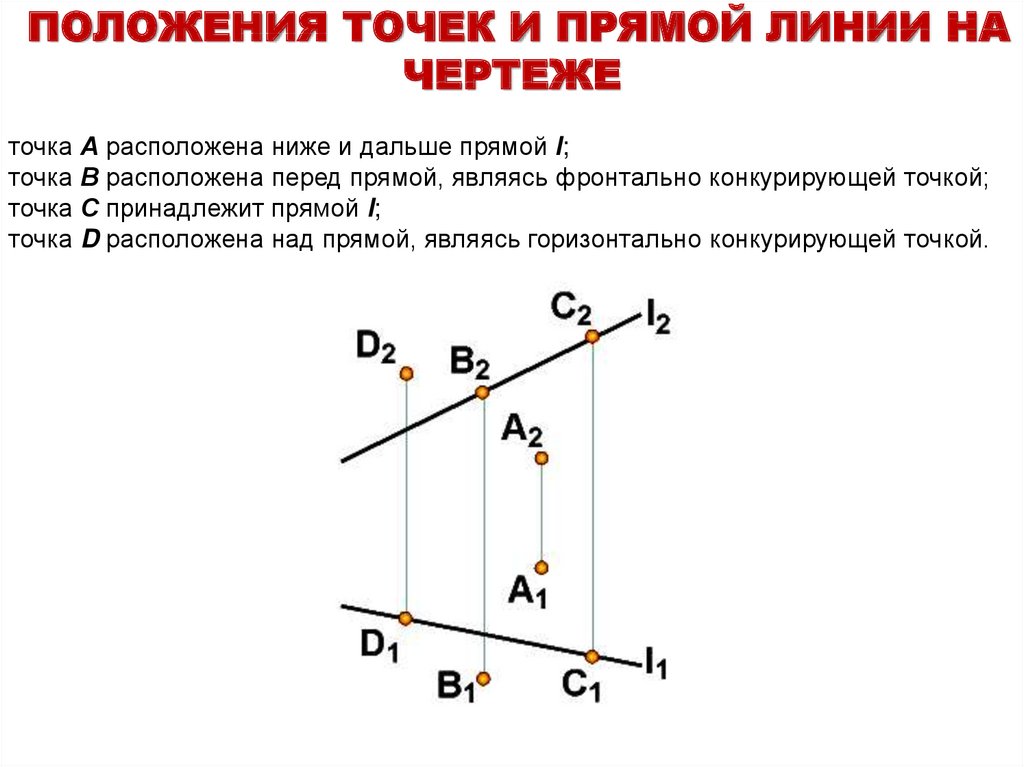
ПОЛОЖЕНИЯ ТОЧЕК И ПРЯМОЙ ЛИНИИ НА
ЧЕРТЕЖЕ
точка А расположена ниже и дальше прямой l;
точка В расположена перед прямой, являясь фронтально конкурирующей точкой;
точка С принадлежит прямой l;
точка D расположена над прямой, являясь горизонтально конкурирующей точкой.

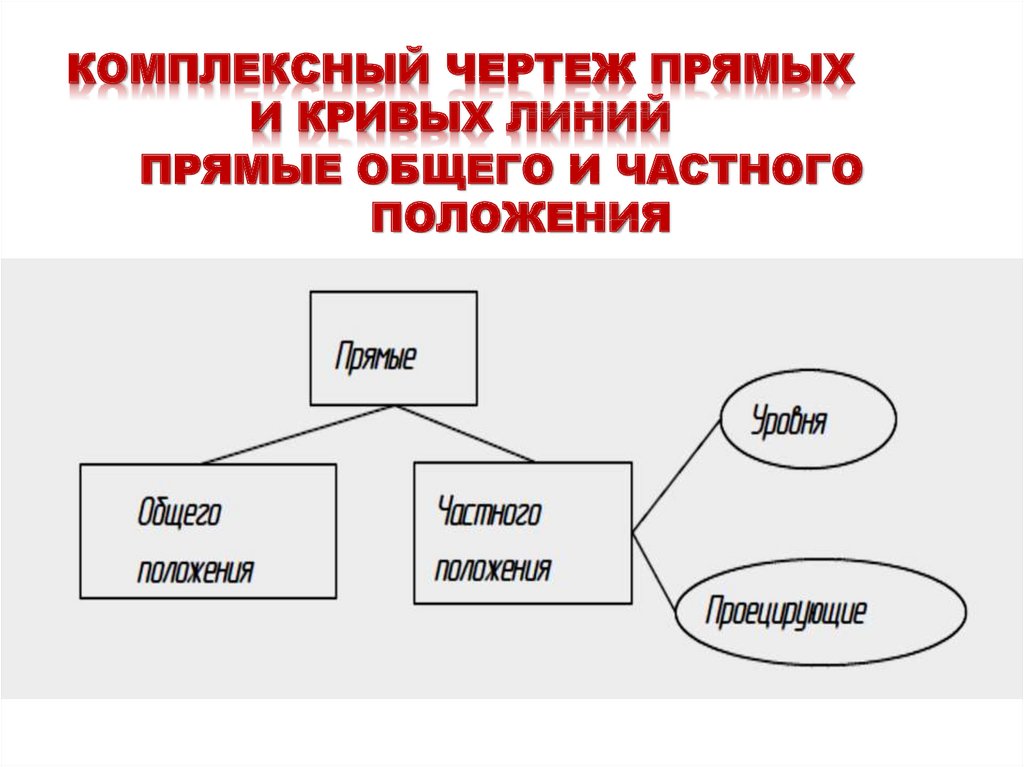
6. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ПРЯМЫХ И КРИВЫХ ЛИНИЙ

ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО
ПОЛОЖЕНИЯ

7.

Чтобы задать положение прямой линии в пространстве,
достаточно задать положение любых двух её точек.
По расположению прямых относительно основных плоскостей
проекций различают прямые общего и частного положения.
Прямая общего положения расположена произвольно
относительно основных плоскостей проекций, а её проекции образуют с
линиями связи углы, отличные от 0 и 90 град.
Прямые частного положения – это прямые, лежащие в
плоскости, параллельной одной из основных плоскостей проекций.
Среди прямых линий частного положения различают
проецирующие прямые и прямые уровня.
Проецирующие прямые линии:
Горизонтально проецирующие прямые, перпендикулярные горизонтальной
плоскости проекций.
Фронтально проецирующие прямые, перпендикулярные фронтальной плоскости
проекций.
Профильно проецирующие прямые, перпендикулярные профильной плоскости
проекций.
Прямые уровня
Горизонталь (h) – прямая, параллельная горизонтальной плоскости
проекций;
Фронталь (f) – прямая линия, параллельная фронтальной плоскости проекций;
Профильная прямая (p) – прямая, параллельная профильной плоскости
проекций.

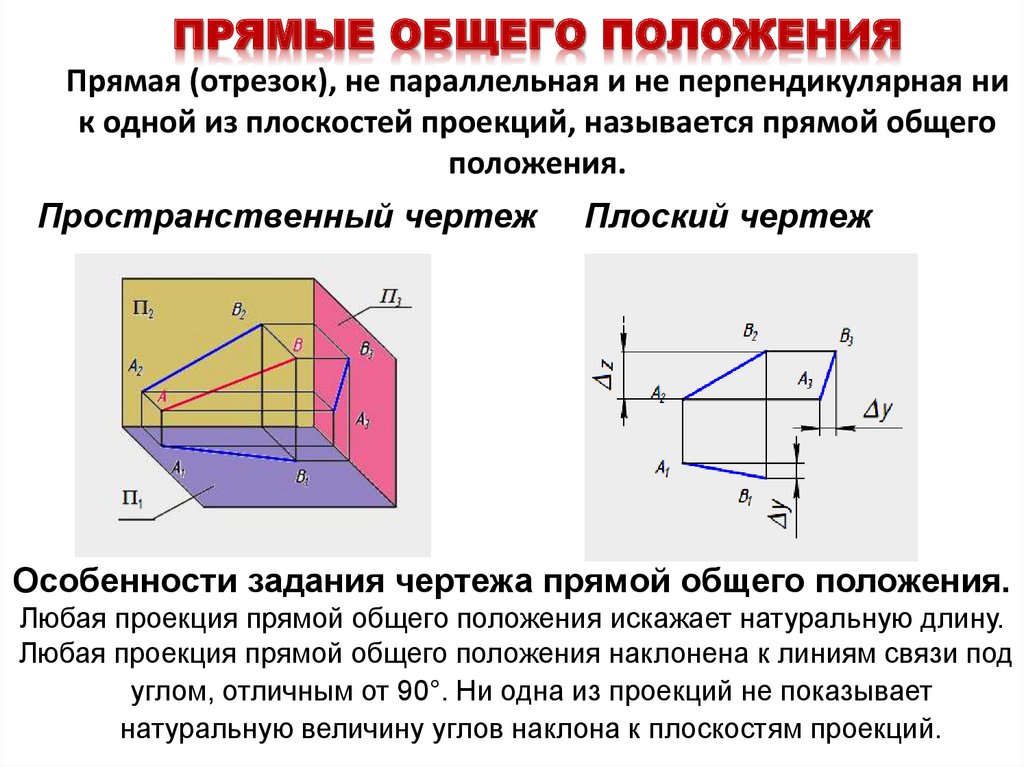
8. ПРЯМЫЕ ОБЩЕГО ПОЛОЖЕНИЯ Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется

прямой общего
положения.
Пространственный чертеж
Плоский чертеж
Особенности задания чертежа прямой общего положения.
Любая проекция прямой общего положения искажает натуральную длину.
Любая проекция прямой общего положения наклонена к линиям связи под
углом, отличным от 90°. Ни одна из проекций не показывает
натуральную величину углов наклона к плоскостям проекций.

9.

МЕТОД ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА ДЛЯ РЕШЕНИЯ
МЕТРИЧЕСКИХ ЗАДАЧ С ПРЯМОЙ
ОБЩЕГО ПОЛОЖЕНИЯ

10.

ПРЯМЫЕ УРОВНЯ
Прямые уровня
– это все не проецирующие прямые, которые
лежат в плоскостях, параллельных основным плоскостям проекций. Уровень –
это положение, когда все точки геометрической фигуры находятся на одинаковом
расстоянии от параллельной ей плоскости проекций.
Различают следующие разновидности прямых уровня:
Горизонталь (h) – прямая,
проекций;
параллельная горизонтальной плоскости
Фронталь (f) – прямая линия, параллельная фронтальной плоскости
проекций;
Профильная прямая (p) – прямая, параллельная профильной плоскости
проекций.

11.

ГОРИЗОНТАЛЬ (h) – прямая // П1
Пространственный чертеж
- угол наклона h к П2
Плоский чертеж

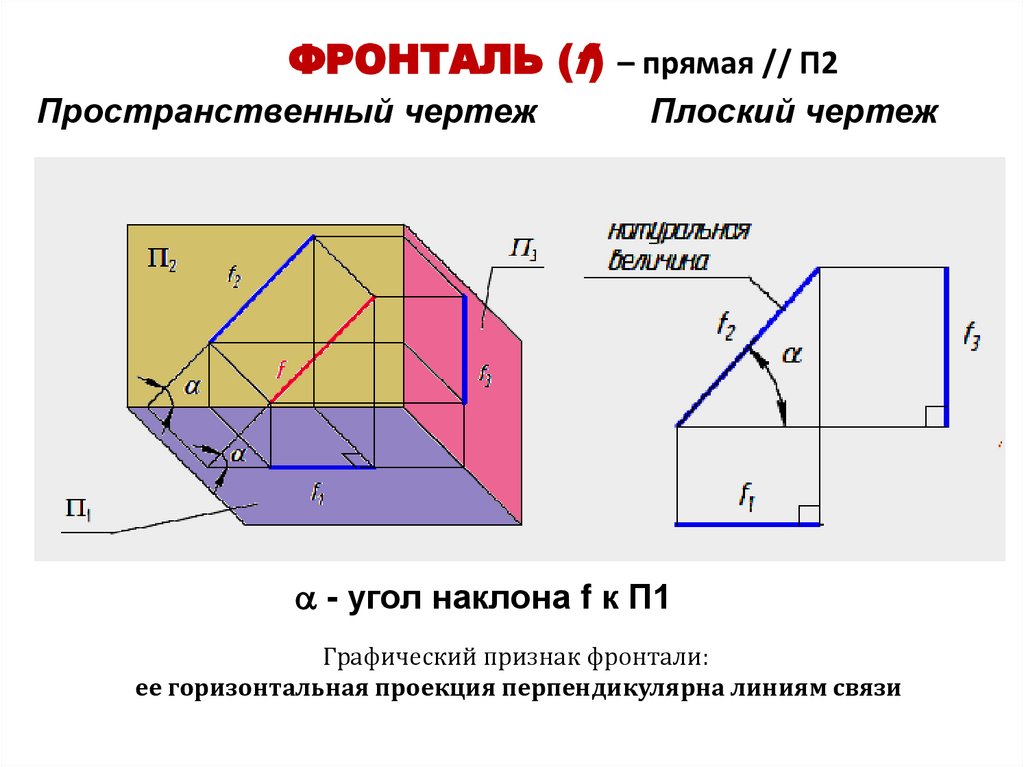
12. ФРОНТАЛЬ (f) – прямая // П2

Пространственный чертеж
Плоский чертеж
- угол наклона f к П1
Графический признак фронтали:
ее горизонтальная проекция перпендикулярна линиям связи

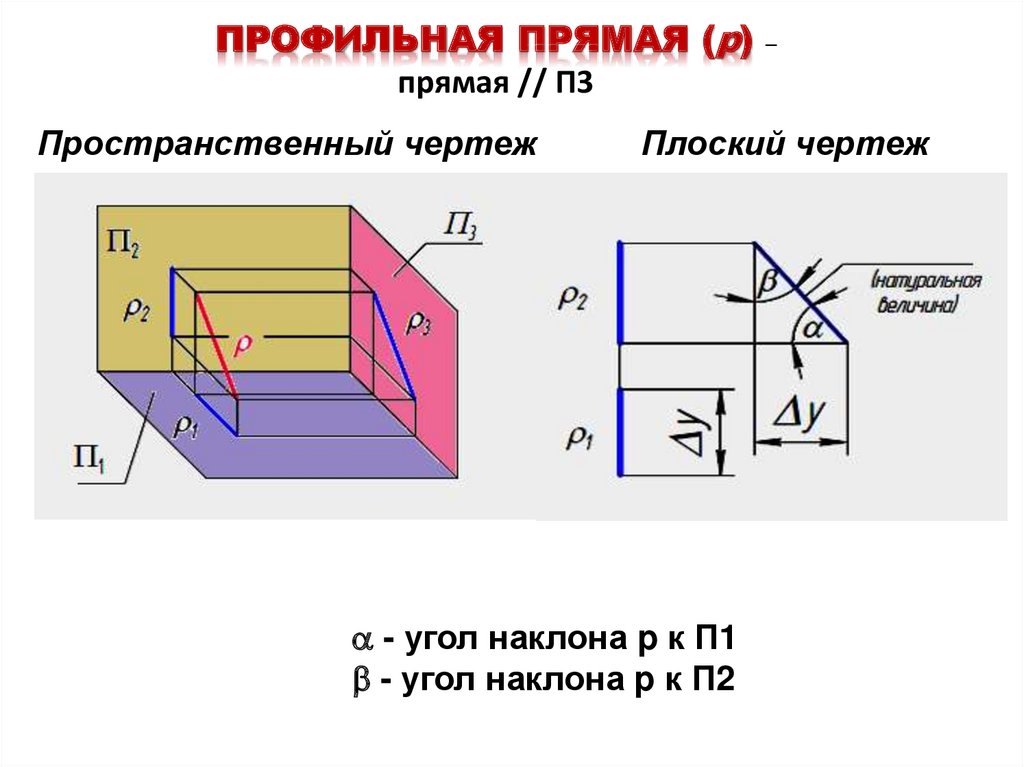
13. ПРОФИЛЬНАЯ ПРЯМАЯ (p) – прямая // П3

ПРОФИЛЬНАЯ ПРЯМАЯ (p)
прямая // П3
Пространственный чертеж
–
Плоский чертеж
- угол наклона p к П1
- угол наклона p к П2

14. ОСОБЕННОСТИ ЗАДАНИЯ ПРЯМЫХ УРОВНЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ

1. Одна из проекций прямых уровня перпендикулярна линиям
связи установленного направления
2. Одна из проекций прямой уровня параллельна самой прямой
и дает истинную величину, а также показывает без
вспомогательных построений угол наклона к одной из
плоскостей проекций

15. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ Прямые, перпендикулярные какой - либо плоскости проекций, называются проецирующими прямыми.

ГОРИЗОНТАЛЬНО ПРОЕЦИРУЮЩАЯ
ПРЯМАЯ
А и В горизонтально конкурирующие точки.
Конкурирующие точки – точки, проекции которых
совпадают на одной из плоскостей проекций.

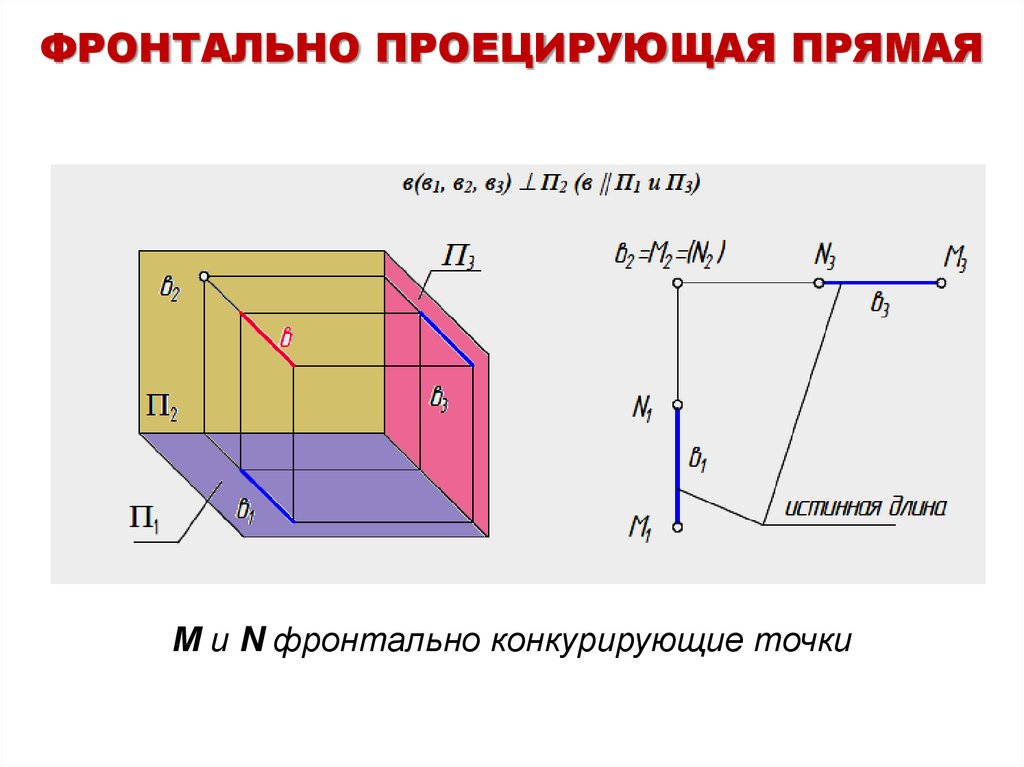
16.

ФРОНТАЛЬНО ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
М и N фронтально конкурирующие точки

17.

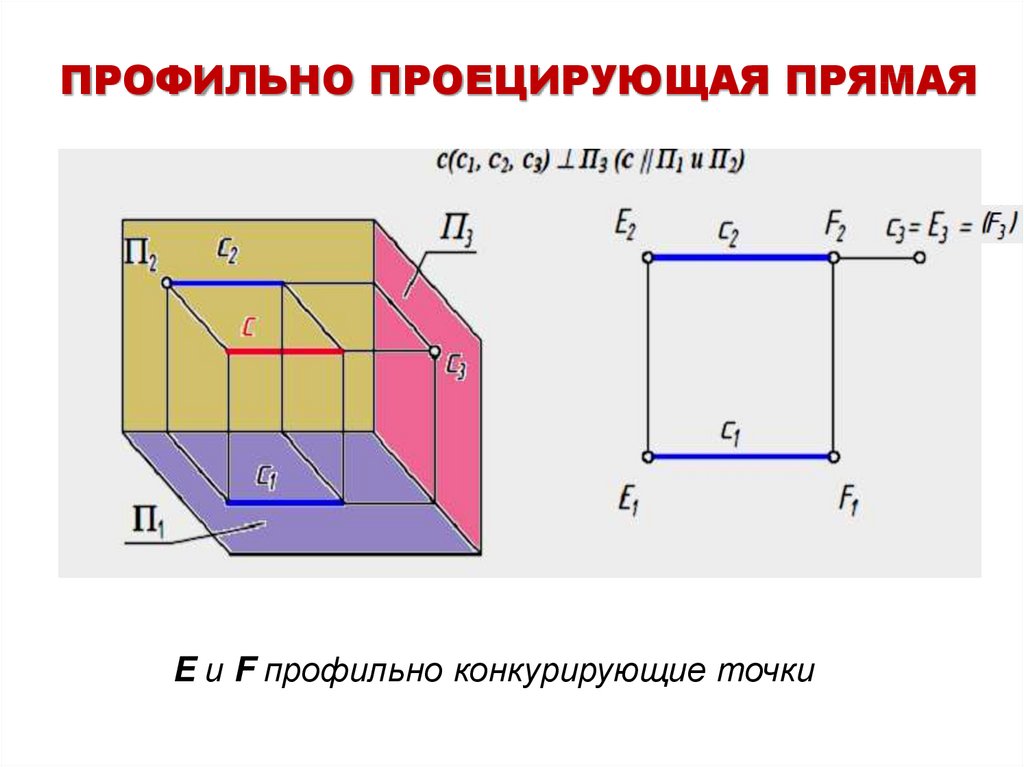
ПРОФИЛЬНО ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
E и F профильно конкурирующие точки

18.

ОСОБЕННОСТИ ПРОЕКЦИЙ
ПРОЕЦИРУЮЩИХ ПРЯМЫХ
Проекция проецирующей прямой на
перпендикулярную ей плоскость представляет
собой точку. Эту проекцию называют главной
проекцией прямой. Она обладает собирательным
свойством - является геометрическим местом проекций
всех точек этой прямой.
Другие проекции (не главные) проецирующей
прямой совпадают с линиями связи с главной проекцией,
составляя с ними угол 0 градусов, и равны истинной
величине прямой, поскольку эта прямая параллельна
данным плоскостям проекций.

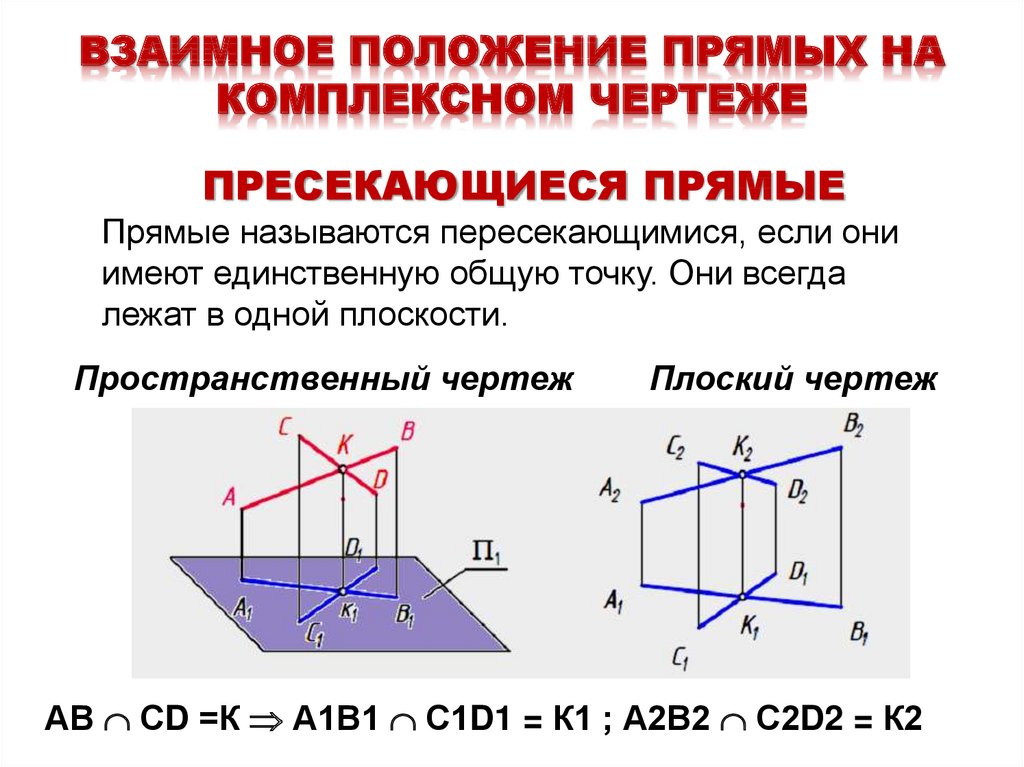
19. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ

ПРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
Прямые называются пересекающимися, если они
имеют единственную общую точку. Они всегда
лежат в одной плоскости.
Пространственный чертеж
Плоский чертеж
АВ СD =К А1В1 С1D1 = К1 ; А2В2 С2D2 = К2

20.

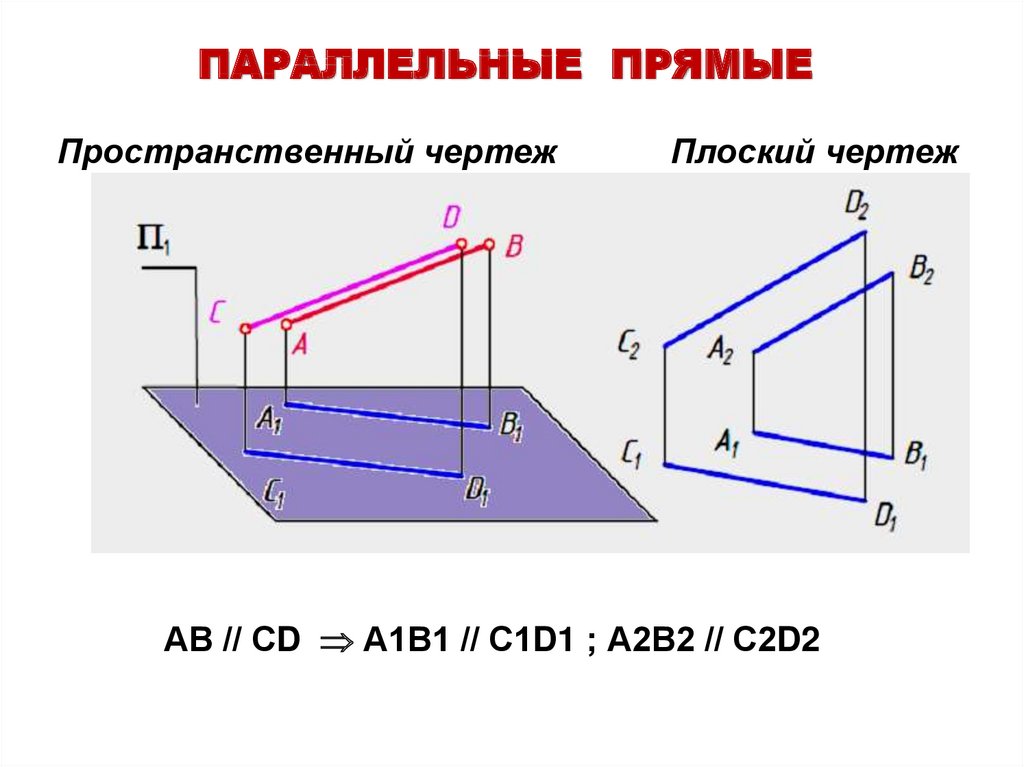
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Пространственный чертеж
Плоский чертеж
АВ // СD А1В1 // С1D1 ; А2В2 // С2D2

21.

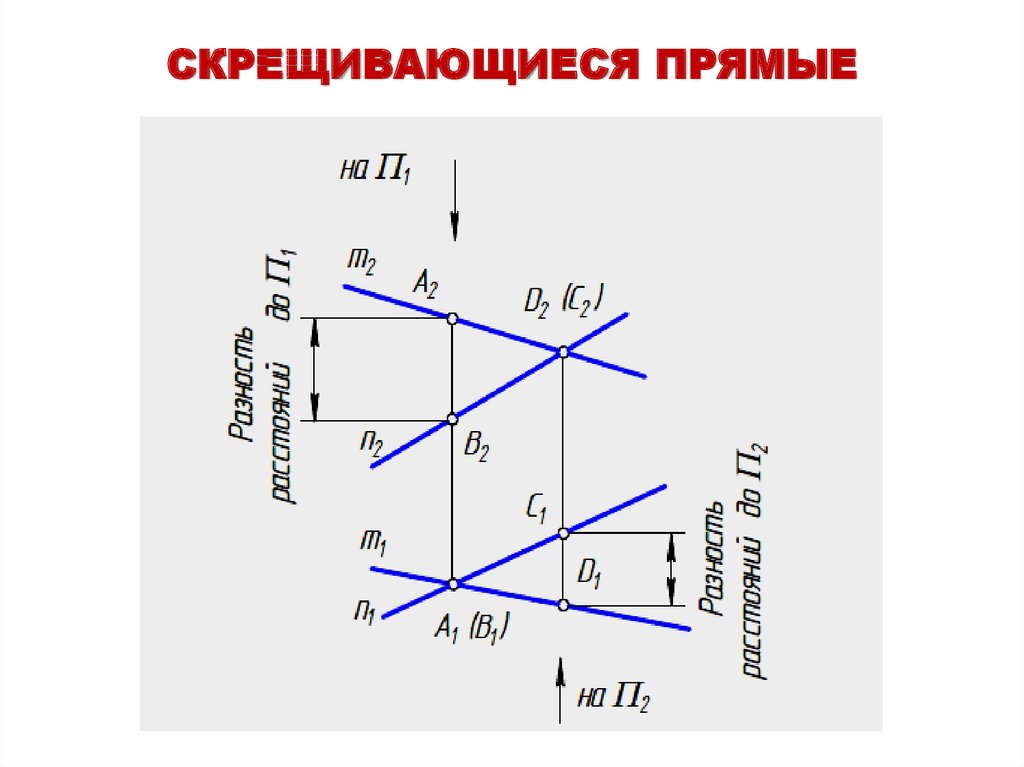
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
Если прямые не параллельны и не пересекаются, то
они называются скрещивающимися прямыми.
Точки А и В - горизонтально конкурирующие.
Точки С и D - фронтально конкурирующие.

22.

СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ

23.

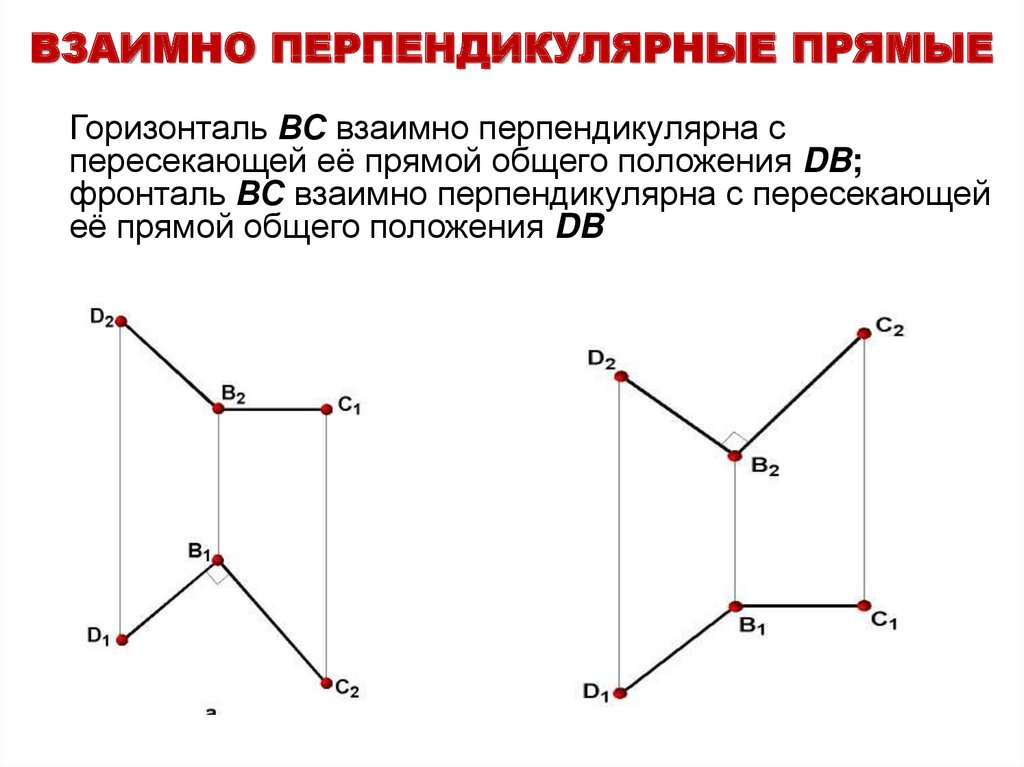
ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Горизонталь ВС взаимно перпендикулярна с
пересекающей её прямой общего положения DB;
фронталь ВС взаимно перпендикулярна с пересекающей
её прямой общего положения DB

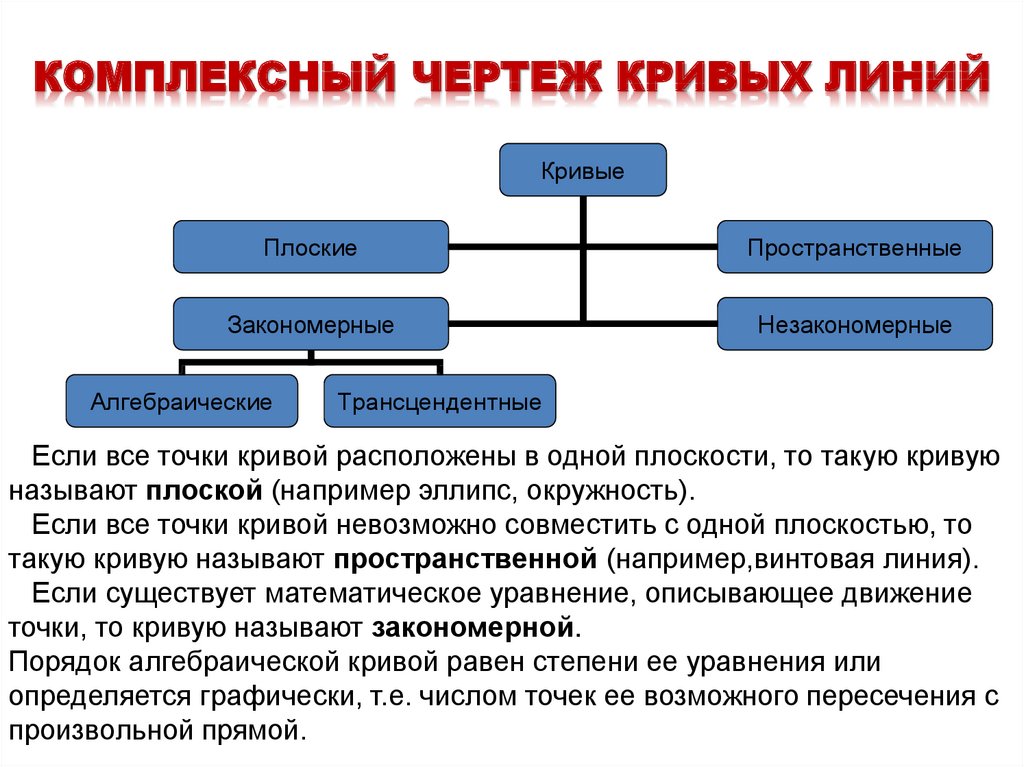
24. КОМПЛЕКСНЫЙ ЧЕРТЕЖ КРИВЫХ ЛИНИЙ

Кривые
Плоские
Пространственные
Закономерные
Незакономерные
Алгебраические
Трансцендентные
Если все точки кривой расположены в одной плоскости, то такую кривую
называют плоской (например эллипс, окружность).
Если все точки кривой невозможно совместить с одной плоскостью, то
такую кривую называют пространственной (например,винтовая линия).
Если существует математическое уравнение, описывающее движение
точки, то кривую называют закономерной.
Порядок алгебраической кривой равен степени ее уравнения или
определяется графически, т.е. числом точек ее возможного пересечения с
произвольной прямой.

25.

СВОЙСТВА ПРОЕКЦИЙ
КРИВЫХ ЛИНИЙ КРИВОЙ
Проекцией кривой линии в общем
случае является кривая линия.
Касательная к кривой
проецируется в касательную к её
проекции.
Несобственная точка кривой
проецируется в несобственную
точку её проекции.
Порядок алгебраической кривой в
проекциях не изменяется.
Число точек пересечения кривой
сохраняется при проецировании.

26.

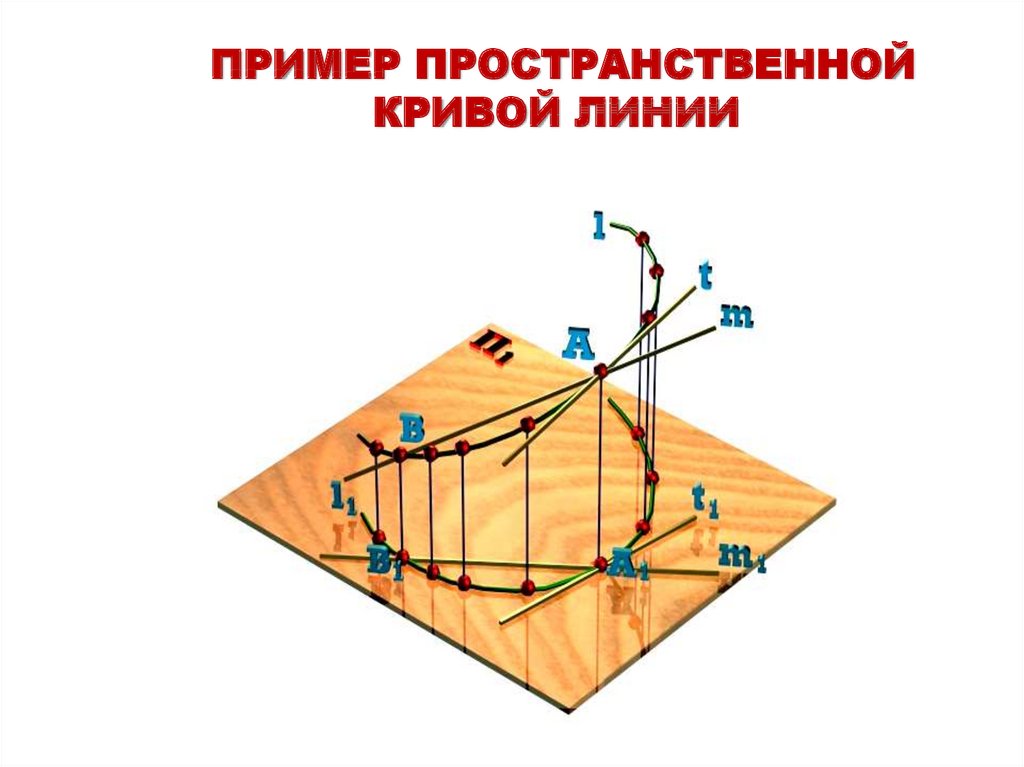
ПРИМЕР ПРОСТРАНСТВЕННОЙ
КРИВОЙ ЛИНИИ

27.

МЕТОД ХОРД
Если хорды кривой пересекаются
значит, кривая линия - плоская.
Хорды не пересекаются, а
скрещиваются значит кривая линия пространственная.

28.

КАСАТЕЛЬНАЯ, НОРМАЛЬ К КРИВОЙ
Касательную (t в точке А) можно рассматривать как предельное
положение секущей, если т.В т.А.
n - нормаль кривой линии в данной точке, n t.

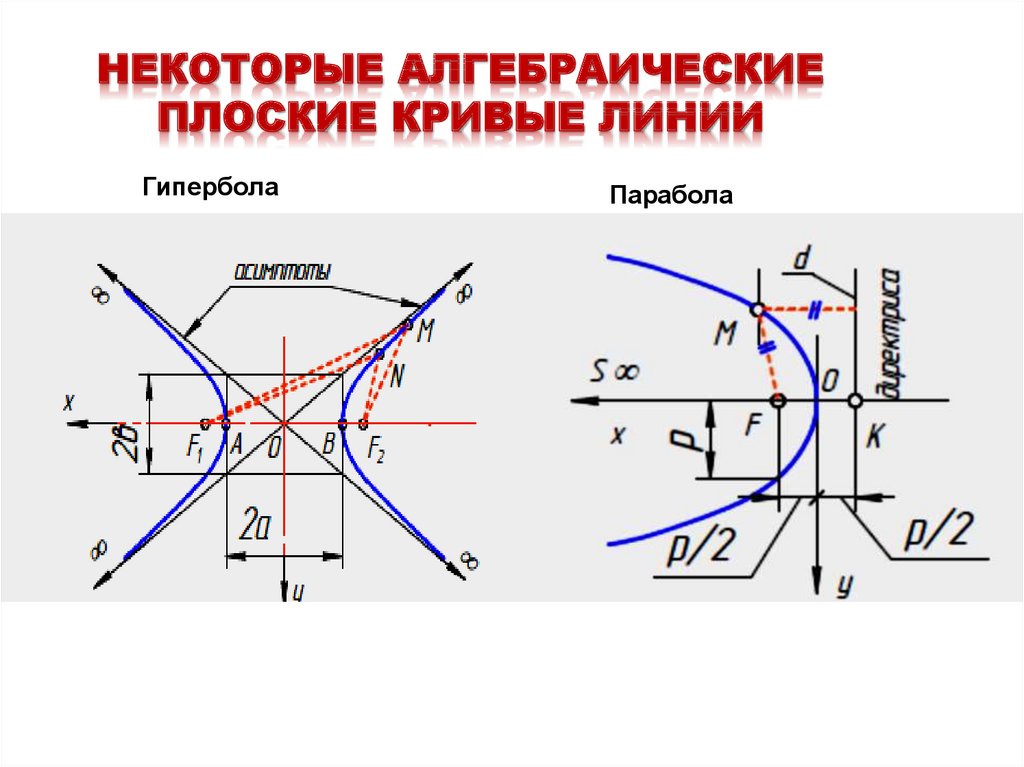
29. НЕКОТОРЫЕ АЛГЕБРАИЧЕСКИЕ ПЛОСКИЕ КРИВЫЕ ЛИНИИ

Гипербола
Парабола

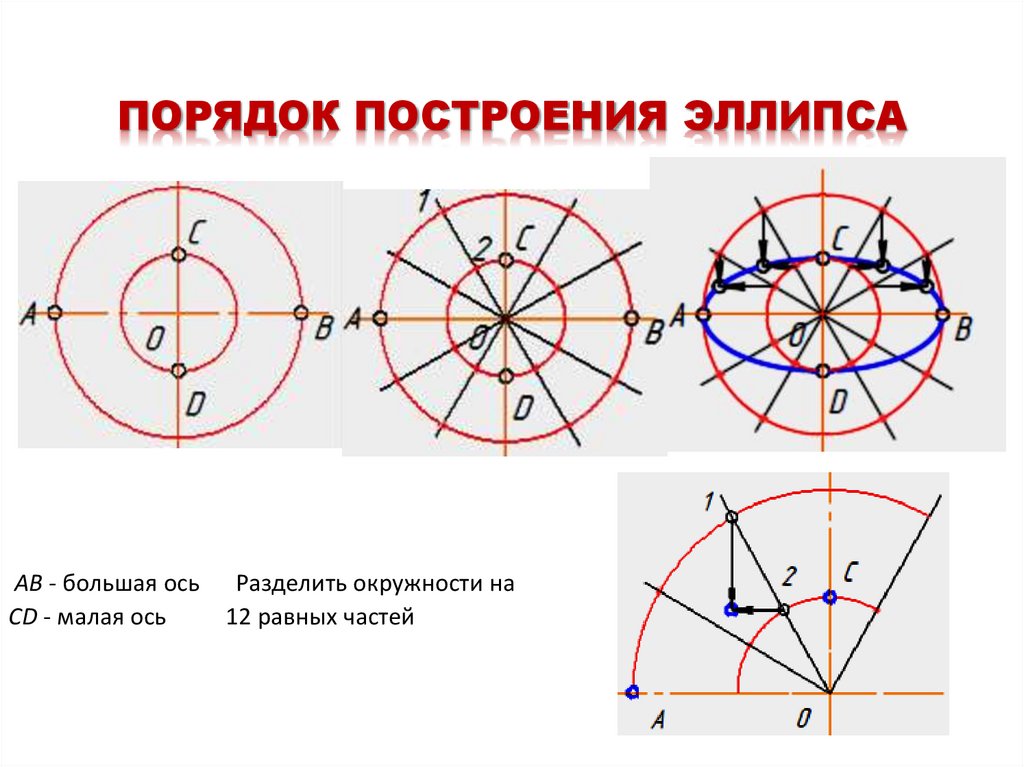
30. ПОРЯДОК ПОСТРОЕНИЯ ЭЛЛИПСА

АВ - большая ось Разделить окружности на
СD - малая ось
12 равных частей

31. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЦИЛИНДРИЧЕСКАЯ ВИНТОВАЯ ЛИНИЯ

Из закономерных
пространственных
кривых наибольшее
практическое
применение находят
винтовые линии:
цилиндрические и
конические
Примеры технического
применения винтовых
линий

32.

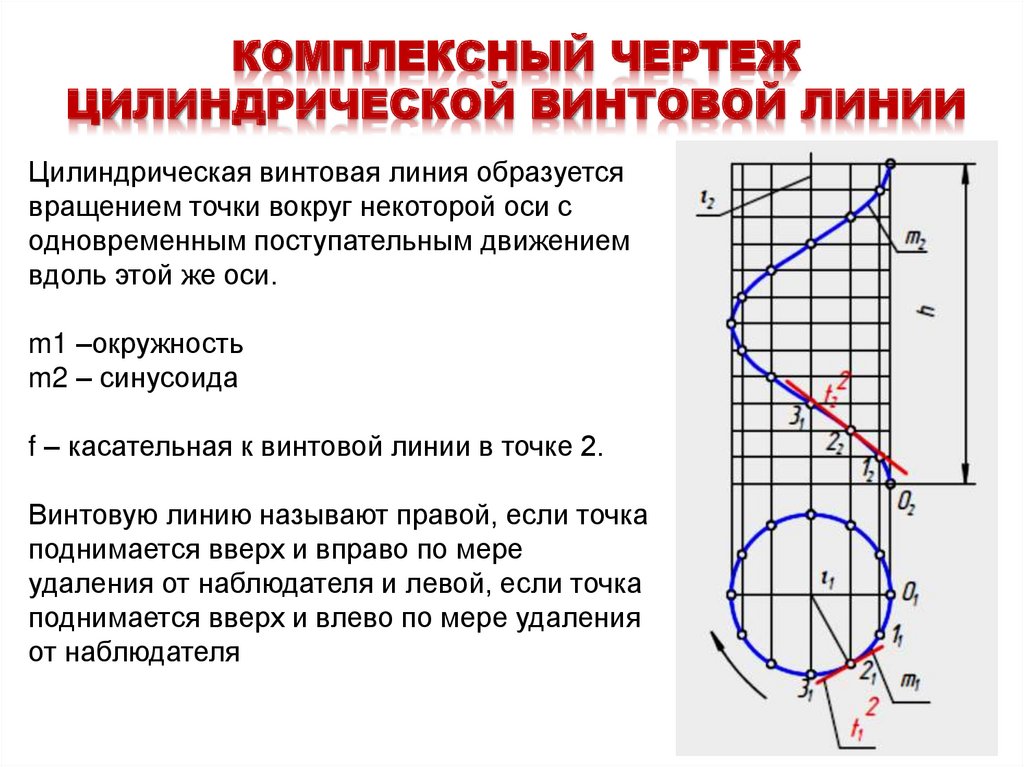
КОМПЛЕКСНЫЙ ЧЕРТЕЖ
ЦИЛИНДРИЧЕСКОЙ ВИНТОВОЙ ЛИНИИ
Цилиндрическая винтовая линия образуется
вращением точки вокруг некоторой оси с
одновременным поступательным движением
вдоль этой же оси.
m1 –окружность
m2 – синусоида
f – касательная к винтовой линии в точке 2.
Винтовую линию называют правой, если точка
поднимается вверх и вправо по мере
удаления от наблюдателя и левой, если точка
поднимается вверх и влево по мере удаления
от наблюдателя