Задание C1

1.

3 х 3 sin
4
cos
x cos 5 х
cos cos sin
sin
б). Найдите все корни этого уравнения,
2 принадлежащие
2 отрезку
а). Решите уравнение
;
2
3 sin 4 х cos 5 х cos 3 х 0
5 х решение
3х
Нам будет удобно записать
3 sin 4 х 2 sin
sin
в виде двух множеств, т.к.
2
аналитическая запись ответа
5 х 3х
0
2
3 sin 4 х 2 sin 4 х sin х 0
в виде:
sin 4для
х 3 2 sin х 0
неудобна
решения двойного неравенства.
sin 4 х 0
4 х n
n
х
4
3 2 sin х 0
-
2 +2 k
3
3
3
sin х
2
n
2
х 1 2 n n х
2 n
3
3
3
+2 k
3
2
3
0

2.

Отбор корней с помощью решения неравенств
;
б). Найдите все корни этого уравнения, принадлежащие отрезку
2
n
х
4
;
2
1
n
1
2
4
2 n 4
n 2, x
2
3
n 3, x
4
n 4,
x
n=2
n=3
n=4
:
4
х 2 n
3
;
:
2
1 1
2n 1
2 3
1
2
2n
6
3
1
3
:2
1
1
n
12
3
n Z
нет значений
n=0
2
х
2 n
3
2
;
1 2
2n 1
2 3
1
1
2n
6
3
2
3
:2
1
1
n
12
6
n 0,
:
2
x
3

3.

а). Решите уравнение
cos 3 х 3 sin 4 x cos 5 х
;
б). Найдите все корни этого уравнения, принадлежащие отрезку
2
а).
n
х ;
4
б).
3
2
;
; ;
.
2
4
3
х 2 n;
3
2
х
2 n
3

4.

;
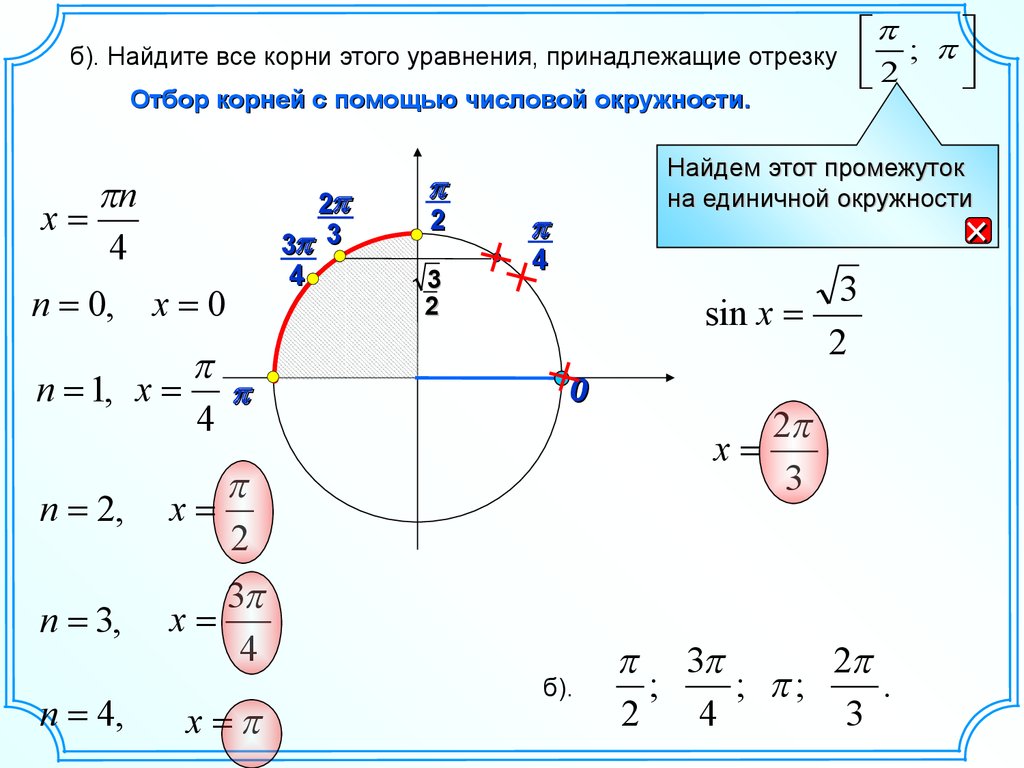
б). Найдите все корни этого уравнения, принадлежащие отрезку
2
Отбор корней с помощью числовой окружности.
n
х
4
n 0, x 0
n 1, x
4
n 2,
n 3,
n 4,
2
3 3
4
2
3
2
Найдем этот промежуток
на единичной окружности
4
3
sin х
2
0
x
2
3
x
4
x
б).
2
x
3
3
2
;
; ;
.
2
4
3