Метод гомогенизации, вариационный подход. (Лекция 12)

1. Введение в асимптотические методы. Лекция 12

Метод гомогенизации:
вариационный подход

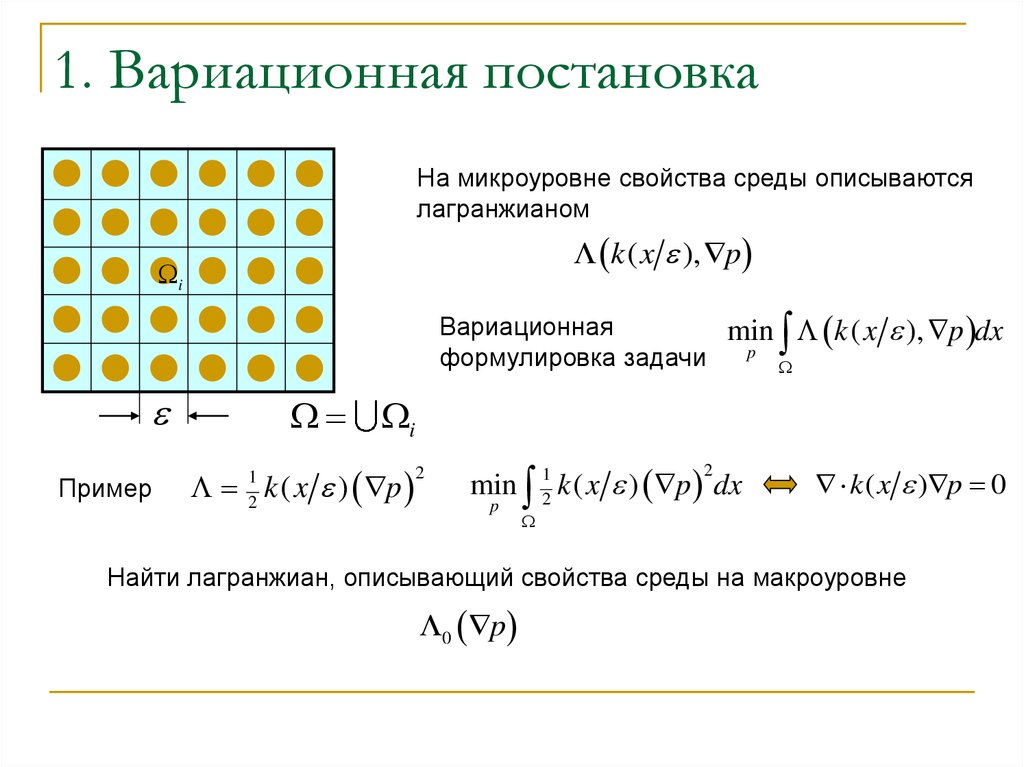
2. 1. Вариационная постановка

На микроуровне свойства среды описываются
лагранжианом
k ( x ), p
i
Вариационная
min k ( x
p
формулировка задачи
Пример
), p dx
i
k ( x ) p
1
2
2
min 12 k ( x ) p dx
2
p
k ( x ) p 0
Найти лагранжиан, описывающий свойства среды на макроуровне
0 p

3. 2. Нахождение макролагранжиана

min k ( x ), p dx
p
p p0 ( x ) p1 ( x, y )
i
тренд+осцилляции
y x/
p1 ( x, y ) периодична по y
p 1 y p x p x p0 y p1 O
min k ( y ), y p1 x p0 dx min i
p0 , p1
p0 , p1
i
k ( y),
y
p1 x p0 dy
i
min i min k ( y ), y p1 x p0 ( xi ) dy min i 0 x p0 ( xi )
p0
i
p1
p0
i
0 x p0 ( xi )
i
min 0 x p0 dx
p0

4. 3. Итог

Макроскопический лагранжиан зависит только от макроскопического
градиента давления 0 p и может быть вычислен как
Пример
0 min
0 min k ( y ),
1
2
1
2
k ( y )
2
k ( y ) 2
k ( y ) k
1
2
k 2 min
1
2
k ( y ) 2
k ( y) k
N ( y)
k ( y )
k ( y ) N i
yi
задачи на ячейке
0 12 k 2 k 12 k k 12 k
N
k 12 k 12 k 12 i j k i
эффективные к-ты
y j
n
n
2 p0 ( x )
N j
0 ( ) 12 kij i j
kij x x 0
kij k ( y ) ij
dy
i 1 j 1
i
j
i, j
Y
yi

5. 4. Двойственная формулировка

Двойственная формулировка max v k ( y ), v
k , преобразование Юнга-Фенхеля k ,
min max v k , v max min v k , v v
Прямая формулировка
0 min k ( y ),
*
0
v 0
*
0
*
Пример
*
v
v
*
v k, v , v 0
max
max v * k , v
v
,
v 0 v 0
0 ( )
1
2
1 1
2
k
max
v
k
(
y
)
v
ij i j
2
v 0
i, j
Оценка
0 max V
V
1
2
k
1
V
2
Vmax k
1 1
12 kharm 2

6. 5.Общие результаты

Если микроскопические свойства среды описываются лагранжианом
(1)
k ( y), p
1
2
(1a)
k ( y ) p
2
То макроскопические свойства могут быть описана лагранжианом
(2)
0 p
(2a)
1
2
p p
kij
xi x j
i, j
а функция 0 может быть найдена на основе прямого (в давлениях) или
двойственного (в потоках) вариационного принципа для задачи на ячейке
(3)
(4)
прямой:
0 min k ( y ),
min
1
2
k ( y)
2
Двойственный:
0 max v k ( y ), v
*
v 0
max v 12 k 1 ( y )v 2
v 0

7. 6. Еще один общий результат

Аналогичные формулы могут быть получены
для двойственного макроскопического
вариационного принципа
(1)
0 max *0
(2)
0 max v * k ( y ), v
v 0
*0 max 0
потому что
f ** f
Двойственный ВП для
задачи на ячейке
max max v * k ( y), v
v 0
v
max min * k ( y ), v
v 0
Сравнение (1) и (2) дает
v
(3)
min k ( y), v
*
0
*
v 0
v
Для сучая 1-D
*0 * k ( y ),

8. 7. 1-D Пример

При гомогенизации могут возникать свойства, отсутствующие на микроуровне
Нелинейная фильтрация с микролагранжианом
Коэффициент
(1)
a
*0 ( )
( y) a
( y)
,
1
1
1
a dp
dx
1
dp
q a
dx
1
эргодическое случайное поле (простр. среднее = среднее по ансамблю )
1
*
(2)
0 ( ) aM
a
Макроскопические свойства зависят от
плотности распределения . Возможно,
что матожидание (2) будет конечным
только при достаточно малых потоках
Макро поток
Пусть
a константа, функция y ,
Макро градиент

9. 8. 1-D Пример

Плотность распределения
(2)
(3)
c
b 1
1
exp c 1 Гамма распределение
(b)
0 1
( 0 1)2
2
2
c
,b
0 M , M 0
2
2
1
b c
ac e 1
b 1 c
*0 ( )
1
e d
(b) 1
a
f ( )
Если ae то (3) расходится, независимо
от значения параметра b.
Расходимость из-за больших
Малое число слоев с большими
определяют режим течения при
больших градиентах давления.
2
c
Микро поток
(1)
b
2
2
a
not
important
1
Микро градиент давления

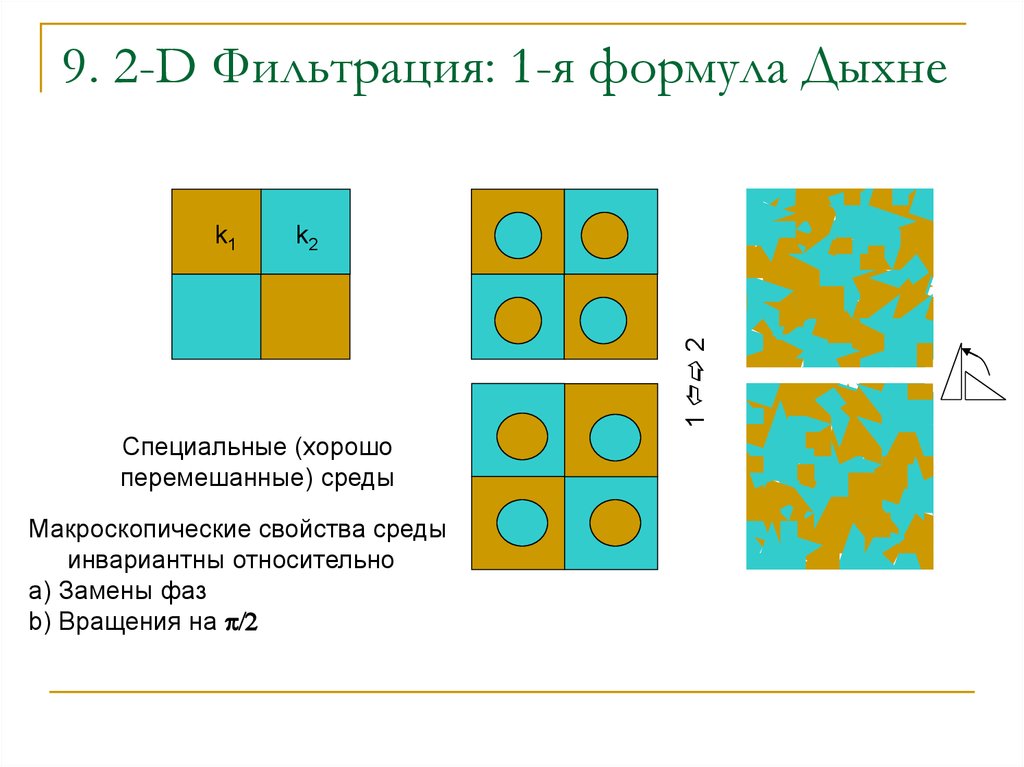
10. 9. 2-D Фильтрация: 1-я формула Дыхне

k2
1 dc 2
k1
Специальные (хорошо
перемешанные) среды
Макроскопические свойства среды
инвариантны относительно
a) Замены фаз
b) Вращения на p/2

11. 10. 2-D Фильтрация: 1-я формула Дыхне

(1) ( ) min
k ( y),
k ( y)
0
(2)
2
1
2
*0 min
v 0
1
2
k 1 ( y )v 2 min
v 0
v
1
2
k 1 ( y ) v
* k ( y), v
2
v 0
v1 2 , v2 1 , ограничена (как и в(1) !!).
(3)
min
*
0
min
(4)
1
2
1
2
k ( y1, y2 ) 1 2 2 1
1
k 1 ( y2, y1 )
2
2
min
1
2
2
k 1 ( y1, y2 )
2
p/2 инвариантность
k1k2 , k1k2 0 ( ) * ( k1k2 )
(5)
0
k1k2 / k y k1
инвариантность
y
+
2
по замене фаз
Окончательное уравнение

12. 11. 2-D Фильтрация: 1-я формула Дыхне

Решением уравнения 0 ( ) 0 (b ) является
*
1
2
b 2
Проверка для линейной изотропной среды:
0 ( ) 12 k? 2 , *0 ( ) 12 k? 1 2
k? b2 k? 1
k? b
Доказательство в общем случае:
a) ( x) * ( x* ) x x* (непосредственно из определения преобразования Ю-Ф )
b)
x* bx ( x) * (bx) bx 2
и ( x) * (bx) ( x) 12 bx 2
c) * ( x* ) sup x x* ( x) sup x x* 1 bx 2 1 b 1 x*2
2
2
x
d)
x
x* bx и ( x) * (bx) ( x) 12 bx 2
Окончательный результат: “хорошо перемешанная” среда макроскопически
изотропна, а ее проницаемость равна
k geom k1k2