Similar presentations:
Сращивание асимптотических разложений. Логарифмы. (Лекция 7)
1. Введение в асимптотические методы. Лекция 7
Сращивание асимптотическихразложения: логарифмы
2. 1. Модельная задача: постановка и возникающие трудности
Модельная задача:f 2r 1 f ff 0,
r 2 r 2 f
АР:
0 :
r 2 r 2 f 0 0,
1 :
r 2 r 2 f 2 f 0 f 0 r 3 r 2 ,
f 0 (1) 0,
f 0 ( ) 1
f 1 0,
f 1
f f 0 (r ) f 2 (r )
f 0 1 r 1
f 2 (1) 0
f 2 ln r r 1 ln r A2 1 r 1
f 2 ( ) 0
Невозможно удовлетворить граничному условию
Трудность – из-за неравномерности асимптотики при больших r
1
r 1: f 0 2r 3 , f 0 f 0 r 2 f 0 f 0 не мал при r
r 1 : f 0 f 2 1 ln 1
Разумно испытать асимптотическую последовательность 1, ln 1 ,
3. 2. Внешнее разложение
f 2r 1 f ff 0,f 1 0,
f 1
r фиксировано 0
АР:
0 :
ln 1 :
:
f
r 2 r 2 f 0 0,
r 2 r 2 f 0,
1
f 0 ln 1 f1 f 2
f 0 (1) 0,
f 0 ( ) 1
f1 (1) 0
f 2 ln r r 1 ln r A2 1 r 1
f 0 1 r 1
f1 A1 1 r 1
Константы A1 , A2 будут находиться сращиванием с внутренним разложением
4. 3. Внутреннее разложение
f 2r 1 f ff 0,f 1 0,
f 1
ПС координата
r
фиксировано
0
f ( r, ) F ( , )
F 2 1F FF 0
F 1 ln 1F1 ( ) F2 ( )
e F 0,
Fi 2 1 1 Fi 0
2
i
Fi ( ) 0
Fi ( ) Bi e 2d
Константы B1 , B2 будут находиться сращиванием с внешним разложением.
Для сращивания нужно знать поведение интеграла при 0
5. 4. Внутреннее разложение
f 1 0,f 2r 1 f ff 0,
E2 ( ) e d e d
1
2
1
e d ln
1
1
[
0:
2
e
d
e
d
ln e ln d
0
0
ln e ln d e ln d
const
1
1
f 1
O ln 1
ln 1 12 o( )
]
0.57722
6. 5. Сращивание
f 2r 1 f ff 0,Рассматриваем оба разложения в области их перекрытия:
1
Вводим промежуточную переменную:
r / 1 ,
r 1, 1
В области перекрытия 1 ,
внешнее
разложение:
внутреннее
разложение:
сравнение
разложений:
f 1 0,
f 1
r / 1
0 1
f 1 1
ln 1 A1 1 1
ln A2
1
1
ln ln A2 ln
f 1
ln 1 B1 1 1 ( 1) ln 1 ln 1
B2 1 1 ( 1) ln 1 ln 1
ln 1 : 0 B1 1 B1 0
0 : 1 1
1
: 1 B2 1 B2 1 ln : A1 B2 ( 1) A1 1
: A2 ln B2 (ln 1) A2 1
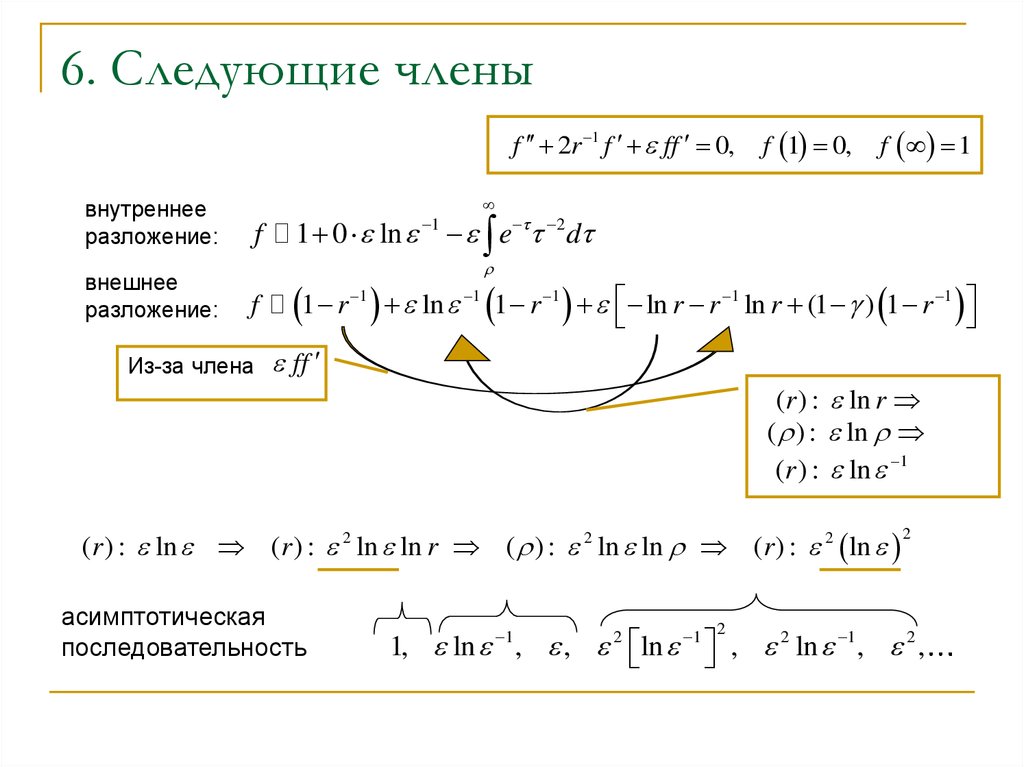
7. 6. Следующие члены
f 2r 1 f ff 0,внутреннее
разложение:
внешнее
разложение:
f
Из-за члена
f 1
1 0 ln e 2 d
1
f
f 1 0,
1 r ln 1 r ln r r
1
1
1
1
ln r (1 ) 1 r 1
ff
(r ) : ln r
( ) : ln
(r ) : ln 1
(r ) : ln (r ) : 2 ln ln r ( ) : 2 ln ln ( r ) : 2 ln
асимптотическая
последовательность
2
2
1, ln , , ln 1 , 2 ln 1 , 2 ,
1
2
8. 7. Правило Ван Дайка и равномерно пригодное АР
E H f H EP
Q
Q
P
f
Правило Ван Дайка работает для P=Q=0 и для P=Q=2
C00 f 1 r 1
2
1
C22 f 1 e d ln 1 1 ln r
r
r
Правило Ван Дайка не работает для P=Q=1
H1E1 f H1 1 r 1 ln 1 1 r 1 H1 1 1 ln 1 1 1
E1 H1 f H1 1 0 ln 1 1
Сращивать надо там,
где меняется степень
1 ln 1
2
1, ln , , ln 1 , 2 ln 1 , 2 ,
1
2
9. 8. Медленное обтекание сферы: постановка задачи
rV
a
(r , ) :
ur r 2 sin , u r r sin
D4 L
(1, ) r (1, ) 0
Re
Va
(r, ) 12 r 2 sin 2
2 sin 1
D 2 2
r
r sin
2
L
1
r 2 sin 2
2 2
2ctg
r
r
D
r
r
r
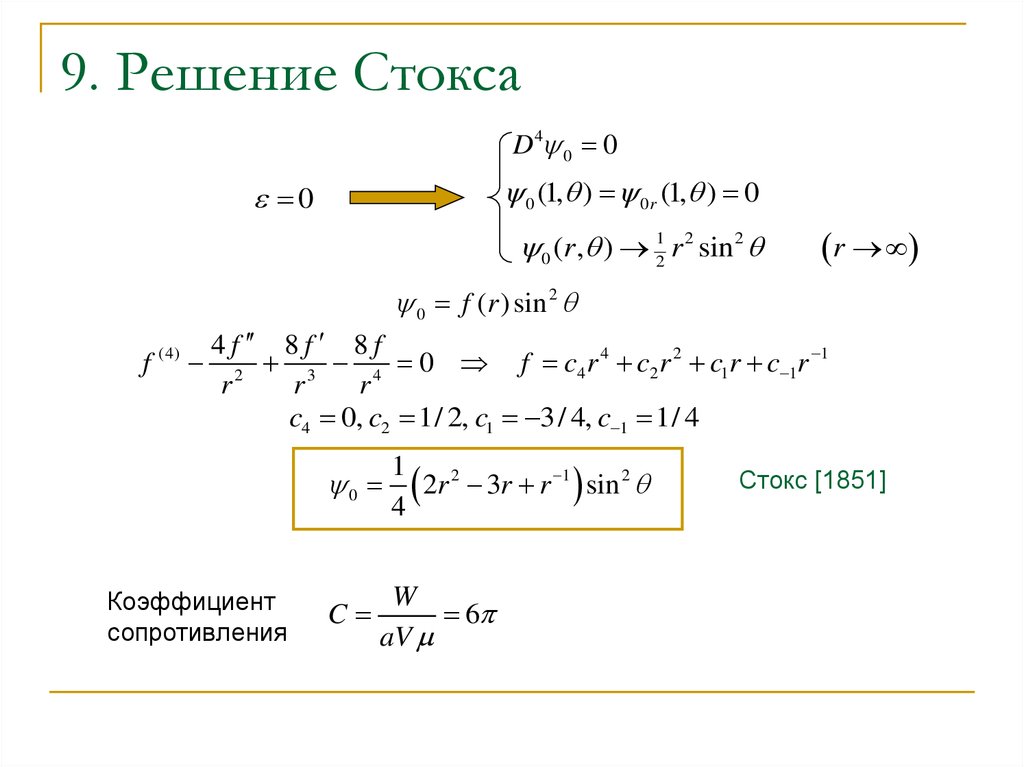
10. 9. Решение Стокса
D 4 0 00 (1, ) 0r (1, ) 0
0
0 (r, ) 12 r 2 sin 2
r
0 f (r ) sin 2
f
(4)
4 f 8 f 8 f
2 3 4 0 f c4 r 4 c2 r 2 c1r c 1r 1
r
r
r
c4 0, c2 1/ 2, c1 3/ 4, c 1 1/ 4
0
Коэффициент
сопротивления
C
1
2r 2 3r r 1 sin 2
4
W
6
aV
Стокс [1851]
11. 10. Формальная поправка к решению Стокса
0 19 2 3 1
D 1 2 3 5 sin 2 cos
4 r
r
r
4
1 (1, ) 1r (1, ) 0
1 o( r 2 ) ( r )
1 g (r ) sin 2 cos
g (4)
12 g 24 g
9 2 3 1
2 3 5
2
3
r
r
4 r
r
r
g b 2r 2 b0 b3r 3 b5r5 163 r 2 329 r 323 r 1
b3 b5 0,
b0 b 2 3/ 32
Уайтхед [1889]
3
1 2r 2 3r 1 r 1 r 2 cos sin 2 A 2r 2 3r r 1 sin 2
32
12. 11. Толщина ПС
12 r 2 sin 21
3
1
2
3
r
r
sin
2r 2 3r 1 r 1 r 2 cos sin 2
4
32
причина неравномерности
Разложение Стокса пригодно пока
мал по сравнению с
Оно становится непригодным если они одного порядка, т.е. если r 1
ПС координата r
Другие соображения:
Озеен [1910]
Инерция = вязкость
V V V p
V 2 V
L2
L
L – характерный масштаб
1
Инерция и вязкость соизмеримы при L
V 1
13. 12. Внутреннее разложение
rфиксировано
0
( r, ) ( , )
0
1
1 2 2
3
2
1
2
2
2
r
3
r
r
sin
sin
sin
O( )
2
4
2
4
1 2 2
1
sin
1 ,
2
2
2
sin 2
D
cos
D 1 0
3
0 : 1 sin 2
4
Уравнение Озеена
3
(1/ 2) 1 cos
1 1 cos 1 e
2
14. 13. Поправка во внешнем разложении
1 2 23
(1/ 2) 1 cos
sin
1
cos
1
e
2
2
2
1
3
(1/ 2) r 1 cos
r 2 sin 2 1 cos 1 e
2
2
1
3
3
r 2 sin 2 r sin 2 r 2 sin 2 1 cos
2
4
16
1
r , 2r 2 3r r 1 sin 2 1
4
9 2 3 1
D 4 1 2 3 5 sin 2 cos
4 r
r
r
1 (1, ) 1r (1, ) 0
3 2 2
C 6 1 83
1
r sin 1 cos (r )
16
3
3
1 2r 2 3r 1 r 1 r 2 cos sin 2 2r 2 3r r 1 sin 2
32
32
15. 14. Метод Озеена: модельная задача
f 1 0,f 2r 1 f ff 0,
f 2r 1 f f 0,
f 1 0,
f 1
f 1
В области конечных r мы
вносим в задачу малую
погрешность, а в области
больших r , там где нелинейный
член важен, погрешность тоже
мала из-за того, что здесь f
близка к единице.
2
f 1 e dt e 2dt
r
1
1
f 1 ln r 1 O ln ln 1 O ln
r
1 r ln r 1
1 r 1
1 ln 1
1 r 1 ln
1 r ln r r
1
1
1
ln r 1 1 r 1
16. 15. Метод Озеена: обтекание сферы
V V V p,V 0
V r 1 0, V e z
V
V p,
z
V 0
V r 1 0, V e z
В области конечных r мы
вносим в задачу малую
погрешность, а в области
больших r , там где нелинейный
член важен, погрешность тоже
мала из-за того, что здесь V
близка к ez.
17. 16. Теплообмен при медленном обтекании цилиндра
V T T ,r x2 y2 1
r
T 0,
r 1
T 1.
Поле скоростей потенциально
На бесконечности
На поверхности цилиндра
-критерий Пекле, характеризующий
отношение конвекции к кондуции
dw
1
, w z ,
dz
z
Vx 1, V y 0
Vn 0
Vx iV y
z x iy
Физика данной задачи полностью отвечает подходу Озеена. При r 1
важен лишь кондуктивный теплоперенос; при больших r , там, где , Vx 1, V y 0
превалирует конвекция.
T
T ,
r x2 y2 1
Подход
x
r
T 0,
Озеена
r 1
T 1.
18. 17. Теплообмен при медленном обтекании цилиндра
TT ,
X x, Y y ,
X
T 0,
X 2 Y 2 r
T 1.
Естественно искать решение этой задачи во всей плоскости, разместив в
начале координат источник неизвестной заранее мощности
T
T Q ( x ) ( y )
X
T
u
X /2 1
X /2
e
u
T e u
X
X
2
1
u u Q ( x ) ( y )
4
u есть функция только !
2
2
u 2u 2T
T
X /2 1
X /2 u
e u
,
e
,
2
2
2
X X Y
Y 2
X
4
1
1 d du
u
0
4
dr d
du
lim
Q
0
d
u QK0 12
T Q e X / 2 K0 12
19. 19. Теплообмен при медленном обтекании цилиндра
T Q e X / 2 K0 12 Q ln 1 OQ
1
ln 1
x/2
eX / 2
e
T
K0 12
K0 12 r
1
1
ln
ln
2
Суммарный тепловой поток
0
T
r
d
r 1
2
ln 1
20. 20. Упражнение к лекции 7
1.Рассмотреть задачу
f 2r 1 f 12 2 1 f 2 0,
Получить внешнее АР по АП
и внутреннее АР ( r)
Срастить разложения.
f (1) 0,
f ( ) 1
1, , 2 ln , 2
Затухающее на бесконечности решение уравнения
y 2 x 1 y y x 2e 2 x
1
x t
x 3t
1
y
Ax
e
e
e
t
dt где A - произвольная константа
есть
2x x
2 A ln 3
ln 3
x 0:
y
ln x A
1
2x
2
1 x
21. 21. Упражнение к лекции 7
2. Рассмотреть задачуПодсказка : АП
3r
f f f 0, r 1
2
f (1) 0, f ( ) 1
f
1, 1/ 2 , ln 1 ,
3. Заменить цилиндр на сферу в задаче о теплообмене тела с
медленным потенциальным потоком обтекающей его
жидкости.



















 mathematics
mathematics