Асимптотические разложения. (Лекция 2)

1. Введение в асимптотические методы. Лекция 2

Асимптотические разложения

2. 1. Сходимость

Ряд
f
n
сходится при фиксированном
( z)
n
z если
N
f
0 N0 ( z, ) : M , N N 0
n
n M
( z)
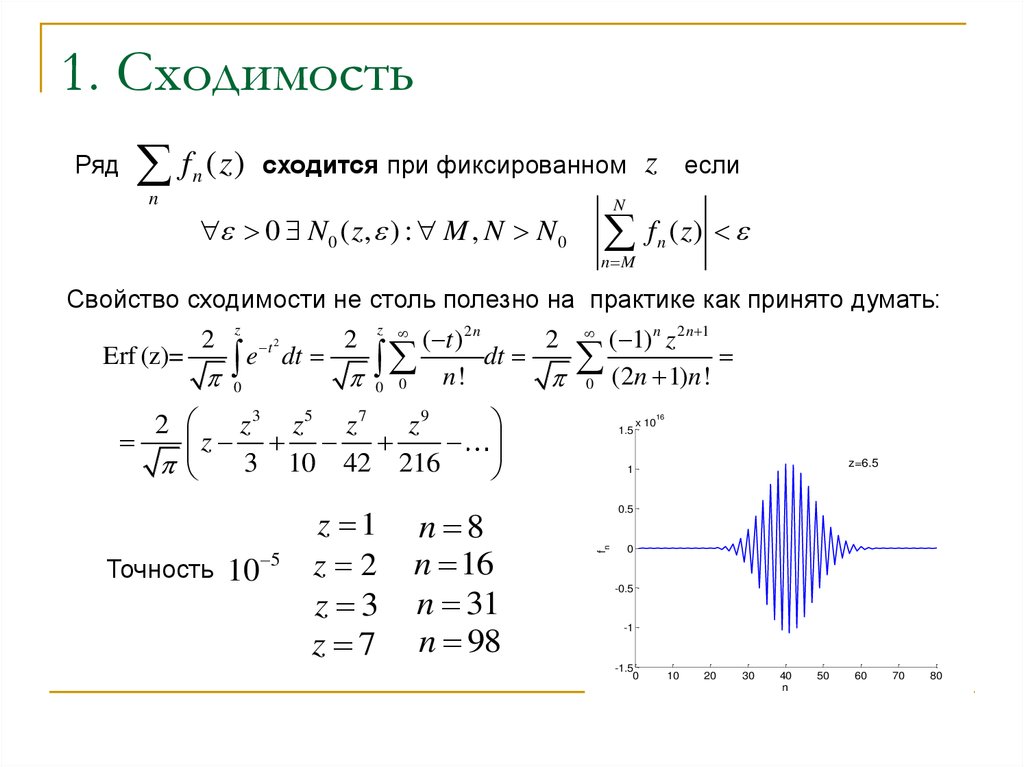
Свойство сходимости не столь полезно на практике как принято думать:
( t ) 2 n
2
Erf (z)=
e
dt
dt
0
0 0 n !
z
t
2
2
z
2
z3 z5 z7
z9
z
3
10
42
216
Точность
10
5
z 1
z 2
z 3
z 7
( 1) n z 2 n 1
0 (2n 1)n!
n 8
n 16
n 31
n 98
16
1.5
x 10
z=6.5
1
0.5
fn
2
0
-0.5
-1
-1.5
0
10
20
30
40
n
50
60
70
80

3. 2. Асимптотичность

Альтернативное выражение для Erf при больших z:
Erf (z)=
Интегрирование
по частям:
10 5
z 2.5 n 3
z 3 n 2
z
2
e dt 1
t 2
t
e
dt
2
z
z
t
t
e
dt
2
0
2
z
2
z
2
t 2
Ряд расходится
de
e
e
2 dt
2t
2 z z 2t
Точность
Erf ( z ) 1
e
2z
z2
e
2z
z2
1
1 3
1 3 5
1
2 z 2 (2 z 2 ) 2 (2 z 2 )3
1
1 3
1 3 5
8
1
O
(
z
)
2
2 2
2 3
2
z
(2
z
)
(2
z
)
Это разложение обладает тем важным свойством, что (при больших z) главный
член дает очень хорошее приближение, а последующие члены все в меньшей и
меньшей степени его корректируют. Такого сорта разложения называют асимптотическими. Более конкретно, в данном случае мы имеем дело с асимптотическим
k
разложением функции Erf z по степеням z
при z

4. 3. Асимптотичность и сходимость

Идеология работы с асимптотическими разложениями в корне
отличается от работы со сходящимися рядами.
Сходимость требует, чтобы при n члены ряда быстро
убывали. Не обязательно сразу, рано или поздно.
Асимптотичность требует чтобы уже главный член был хорошим
приближением при z . Поэтому, как правило, он вполне
достаточен, если нас интересует указанная асимптотика. Лишь в том
случае, когда он тривиален (как в рассмотренном примере) нужен
следующий член.
Определенные проблемы возникают, если значение z не достаточно велико. Добавка нескольких дополнительных членов в этом
случае оказывается полезной. Общим правилом является
ограничение их количества требованием того, чтобы следующий
член разложения был меньше предыдущего.

5. 4. Определения: Асимптотическая последовательность

Последовательность функций 0 ( z ), 1 ( z ), называется
асимптотической последовательностью при z a , если
при всех
z a:
n 1 / n 0
n 1 o n
Примеры
1, z, z 2 , z 3 ,
z 0
1, z1/ 2 , z1 , z 3/ 2 ,
z 0
1, z 1, z 2 , z 3 ,
z

6. 5. Определения: Асимптотическое разложение

Говорят, что функция f ( z ) имеет асимптотическое разложение по
последовательности 0 ( z ), 1 ( z ), , если существуют константы c0 , c1 ,
такие что, для каждого n N
n
f ( z ) ck k ( z ) o n ( z )
k 0
В этом случае пишут
f ( )
N
c
n 0
n n
z a
( )
Если N то говорят об асимптотическом ряде

7. 6. Единственность

Если асимптотическая последовательность фиксирована и
асимптотическое разложение функции f существует, то
константы ck определяются однозначно.
f ( z ) n ck k ( z )
0
0
lim
z a
n ( z)
f ( z ) 0 ck k ( z )
n 1
n ( z)
f ( z ) 0 ck k ( z ) cn n ( z )
n
n ( z)
n 1
cn lim
z a
n
cn
f ( z ) ck k ( z )
k 0
n ( z)
f ( z ) 0 ck k ( z )
n ( z)

8. 7. АР не обязательно существует

При заданной асимптотической последовательности 0 ( z ), 1 ( z ),
асимптотического разложения f ( z )может не существовать. Это
выражается в том, что предела n 1
f ( z ) ck k ( z )
k 0
cn lim
z a
n ( z)
в этом случае нет (например, он равен бесконечности). Мы
сталкивались с такой ситуацией на предыдущей лекции, когда
пытались формально построить асимптотическое разложение
1 1/ 2
f
1
по целым степеням
Вывод: выбор «родной» асимптотической последовательности для
данной функции является ответственным шагом при построения ее
асимптотического разложения

9. 8. Неединственность

Различные функции могут иметь одинаковое асимптотическое
разложение по заданной асимптотической последовательности,
равно как и заданная функция может иметь различные
асимптотические разложения по разным асимптотическим
последовательностям.
Примеры
tg( ) +
1
3
3
2
15
exp ( )
5
n
n!
( 0)
n 0
sin + 12 (sin )3 83 (sin )5
ch
+ ch
2
3
31
270
5
2
3
exp ( )+exp(- -2 )
n
n!
n 0

10. 9. Операции над АР

Можно складывать, вычитать, делить, умножать. При
этом, возможно, придется расширить
асимптотическую последовательность
Можно подставлять одно АР в другое. При этом,
однако, надо соблюдать осторожность.
2
2
2
2
2
f ( z ) exp( z 2 ) f ( z ( )) exp( 2 ) exp( )e 1
f ( z ( )) f ( 1 ) exp( 2 )
z 1
Можно интегрировать.
В общем случае нельзя дифференцировать.
1
Трудности приходят от членов типа cos( ) которые при дифф-ии дают
1
не ожидаемые O(1) а O( ) . Это не аналитические члены. Если f ( )
аналитична в некотором секторе -плоскости, то в этом секторе можно диф-ть

11. 10. Еще раз о терминологии.

f ( ) O( g ( ))
ограничено
f ( ) o( g ( ))
0
если
f ( )
g ( )
f ( ) g ( )
f ( )
g ( )
при
1
C (C 0, )
0

12. 11. Разложения, зависящие от параметра

В данном курсе мы будем рассматривать главным образом функции
двух (или большего числа) переменных f ( x , ), изучая их
асимптотическое поведение, когда одна из переменных, , мала.
В типичных ситуациях f ( x , ) удовлетворяет некоторому
дифференциальному уравнению по отношению к x , а
выступает в роли параметра задачи.
Естественное обобщение определения асимптотического разложения
f ( x, )
c ( x) ( )
k
k
Если это разложение равномерно пригодным для всех x из области
определения этой переменной, то говорят о регулярном (или
равномерно пригодном), в противном случае – о сингулярном (или
неравномерно пригодном) разложении.

13. 12. Пример 1: внешнее разложение

f ( x, )
1
1 x e
x /
, x 0
«естественное» асимптотическое представление f при
f ( x, )
1
1
1 x 1 x
x O 1
на самом деле верно при
x
совершенно неверный результат в малой окрестности
f (0, ) 1
1
1 1
f (0, )
2 2 4
типичное сингулярное разложение, которое, как говорят,
«разваливается» в окрестности нуля
x 0

14. 13. Пример 1: внутреннее разложение

f ( x, )
1
1 x e
x /
, x 0
причина сингулярности – в том, что предположение о малости
по сравнению с x несправедливо при малых x . Оно нарушается,
когда x есть величина порядка
Перенормировка
X x /
f ( x, ) F ( X , )
F ( X , )
1
1 e X
1 e X
1
1 X
1 X
1
X
1 e
на самом деле верно при
X
1 x
1

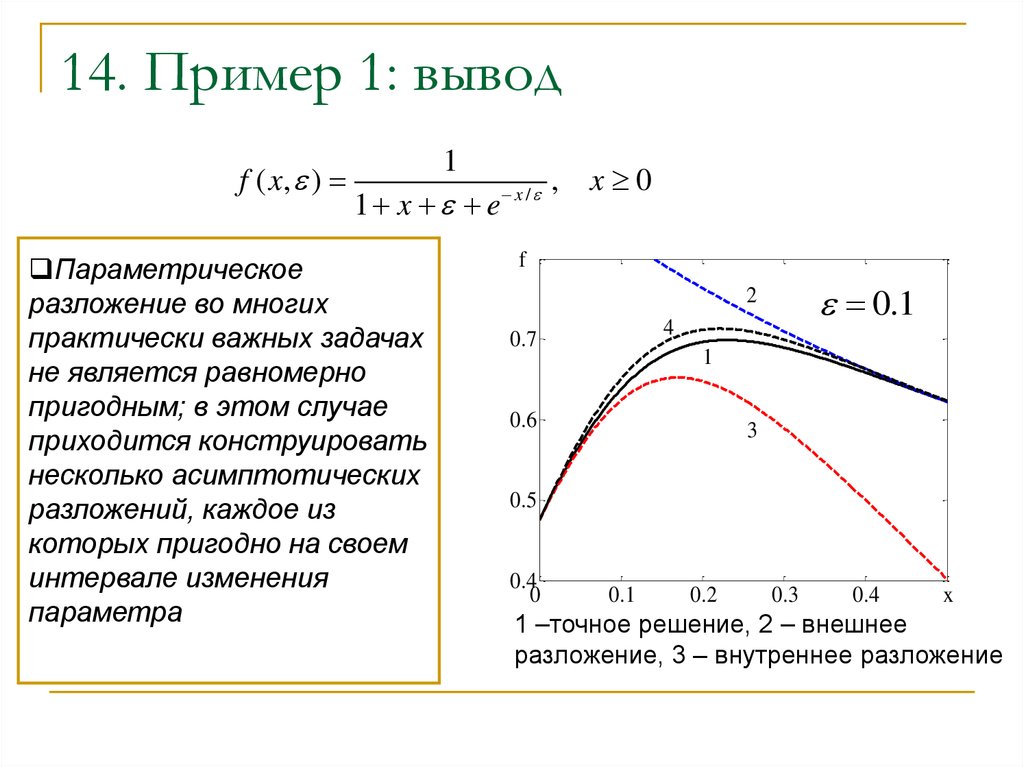
15. 14. Пример 1: вывод

f ( x, )
1
1 x e
Параметрическое
разложение во многих
практически важных задачах
не является равномерно
пригодным; в этом случае
приходится конструировать
несколько асимптотических
разложений, каждое из
которых пригодно на своем
интервале изменения
параметра
x /
, x 0
f
0.1
2
4
0.7
1
0.6
3
0.5
0.4
0
0.1
0.2
0.3
0.4
x
1 –точное решение, 2 – внешнее
разложение, 3 – внутреннее разложение

16. 15. Область перекрытия и промежуточная переменная

f ( x, )
X x /
F ( X , )
1
1 e X
1 X
1
X
1
e
1
1 x e
x /
промежуточная переменная
1
0
x
1
1 e
1
1
1 e
1
1
1
1 x 1 x
x
( ) 0, ( ) 0,
F
f ( x, )
x
X
0
, x 0
1
0
f
1
1
1 1
1 1 1
1
Внешнее и внутреннее разложения идентичны в области перекрытия

17. 16. Сращивание разложений

f ( x, )
1
1 x e
x /
, x 0
Внешнее и внутреннее разложения записываются одинаково при
1
переходе к любой промежуточной переменной x
Можно принять, например p
0 p 1
p 0, p 1
Рассмотрим предельные случаи
Рассматривая случай p 1 , мы должны во внешнем разложении
положить x . Но это, то же самое, что перейти во внешнем
разложении к внутренней переменной .
1
2
2
f
1
1 X O 1 O 1 1 X
1 X 1 X
=
Аналогично при p 0 во внутреннем разложении переходим к
1 1 x
внешней переменной x
F
1
1 x
x
x
1 e
1 e
Внешнее и внутреннее разложения сращиваются друг с другом

18. 17. Принцип сращивания Ван Дайка

E1( n )
оператор, который дает n членов асимптотического
представления функции f ( x , ) для x O 1
E2( m )
оператор, который дает m членов асимптотического
представления функции F ( X , ) для X O 1
Функции f ( x , ) и F ( X , ) идентичны F ( X , ) f ( ( ) X , )
с некоторым множителем ( )
E2( m ) E1( n ) f ( X , ) E1( n ) E2( m ) F ( x, )
обе части при их сравнении, разумеется, должны быть записаны в терминах
одной переменной
m-членное внутреннее разложение n-членного внешнего разложения
должно совпадать с n-членным внешним разложением m-членного
внутреннего разложения.

19. 18. Пример применения

f ( x, ) x
2
, x 0
1 x
1) Строим трехчленное разложение f при x O 1
2 3x 1
(3)
E1 f
n 3, m 2
x 1
2
2
x
8
x
1
x
2) Строим 2-членное внутреннее разложение той же функции при
X x O 1
(2)
2
E
F
1
X
1
f ( x, ) F ( X , ) (1 X )
,
2
2
1
X
1 X
3) Подставляем во внешнее разложение x X и проводим разложение
полученного выражения по с удержанием 2-х главных членов
E
(2)
2
E
(3)
1
2 1 3 X
f ( X , ) X 1
2
2
2
X
8
X
1
X
X 1
1
1
2 X 8X 2 2 X

20. 19. Пример применения

f ( x, ) x
2
, x 0
n 3, m 2
1 x
4) Подставляем во внутреннее разложение X x и проводим
разложение полученного выражения по с удержанием 3-х главных
членов
(3)
1
E
x
E
F
(
x
,
)
1
1
2 1 x
(2)
2
2
1
2x
2
x 1
2
2 x 8x
1
1
x 1
2
2
2 x 8x
2x
(1)
5) Переходим в E2(2) E1(3) f ( X , ) от переменной X к переменной x
(2)
2
E
E f ( X , )
(3)
1
X x
2 2
x 1
2
2x
2 x 8x
6) Убеждаемся в идентичности выражений (1) и (2).
(2)

21. 20. Составное разложение

.
f n ( x, ), Fm ( X , ) - внешнее и внутреннее разложения
g n ,m ( x , )
- их общая часть в области перекрытия
n ,m ( x, ) f n ( x, ) Fm ( x ( ), ) g n ,m ( x, ) составное (равномерно
пригодное) разложение
f ( x, )
Пример
f
f
f 2 ( x, )
F2 ( X , )
1
1 x e
1
1
,
1 x 1 x
1
1 e X
g22
2,2 ( x, )
x /
, x 0
x O 1
1 X
,
1
X
1 e
X O 1
1 x
1
1
1
1 x 1 x 1 e x
x
1
x
1 e
1 x
n 2, m 2

22. 21. Упражнения к лекции 2

1) Получите асимптотическое разложение при x и выясните,
является оно сходящимся или расходящимся.
sin t
dt
t
x
si( x )
2) Используйте интегрирование по частям для того, чтобы найти
при x асимптотическое разложение интеграла
e xt
I ( x)
dt , x 0
1 t
0
Покажите, что разложение расходится. Получите оценку для остатка
и используйте ее, чтобы найти число членов при данном x ,
минимизирующих погрешность вычисления I ( x )

23. 22. Упражнения к лекции 2

3) Найдите разложения при 0 с точностью до двух членов для
данных ниже функций. Постройте составное разложение
x e x
f ( x, )
,
1 x
1 x
f ( x, ) 1
x