Интегралы, локальные вклады. (Лекция 3)

1. Введение в асимптотические методы. Лекция 3

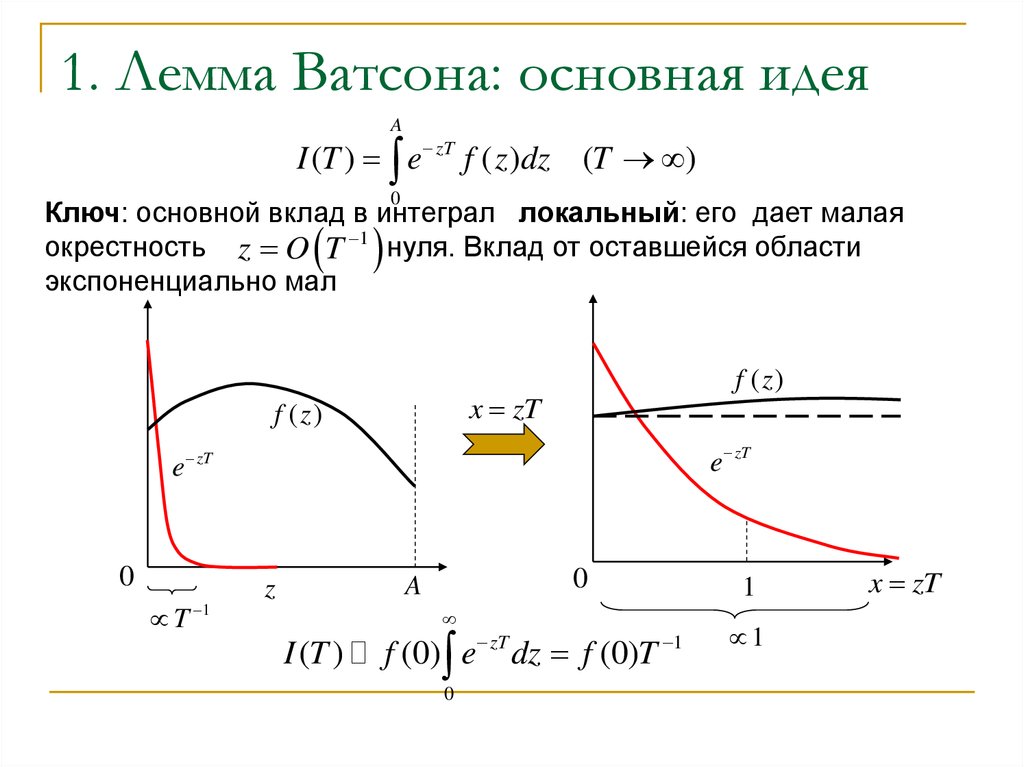
Интегралы: локальные вклады

2. 1. Лемма Ватсона: основная идея

A
I (T ) e zT f ( z )dz (T )
0
Ключ: основной вклад в интеграл локальный: его дает малая
окрестность z O T 1 нуля. Вклад от оставшейся области
экспоненциально мал
f ( z)
x zT
f ( z)
e zT
e zT
0
T
1
0
A
z
I (T )
f (0) e zT dz f (0)T 1
0
1
1
x zT

3. 2. Лемма Ватсона: пример

e xt dt
I ( x)
1 t
0
x
Т.к. основной вклад в интеграл приходит из малой окрестности
точки t=0 естественно разложить подынтегральную функцию в нуле
t
1
k 1
t
1 t k 1
t 1
n
n
и почленно проинтегрировать возникающее разложение
I ( x) e
xt
1 t t
0
Оценка остатка
2
dt 1x x12
1
n 1
n 1 ! R ( x)
xn
n
e txt n
n!
Rn
dt e txt n dt n 1
1 t
x
0
0
показывает, что ряд действительно является асимптотическим

4. 3 Лемма Ватсона: окончательная формулировка

A
I (T ) e Tz f ( z )dz (T )
0
Лемма Ватсона (общий случай)
f
0
1
a0 z a1z
n
I (T )
an z
n
k 1
a
T
( k 1)
k
0
z 0
T
Используется тот факт, что
Tz
1
z
e
dz
(
1)
T
0

5. 4. Пример

Erfc( x)
2
e
t
2
dt t x
x
e x
x
2
А.Р.:
Erfc( x )
2
e
x
2
e
2 x
e
2
d
0
1 1 1 3 2
2 x2 2 x2
Способ 1 : интегрирование по частям исходного интеграла
Способ 2 : раскладываем e
1 2
2
и пользуемся леммой Ватсона
Способ 3 : подчеркивая, что основной вклад приходит из малой x
окрестности нуля вводим перенормировку x u
x2
2e
Erfc( x)
x
2u u
e
e
0
2
/x
2
x2
2e
du
x
2
4
u
u
2u
e
0 1 x2 2 x4
du
1

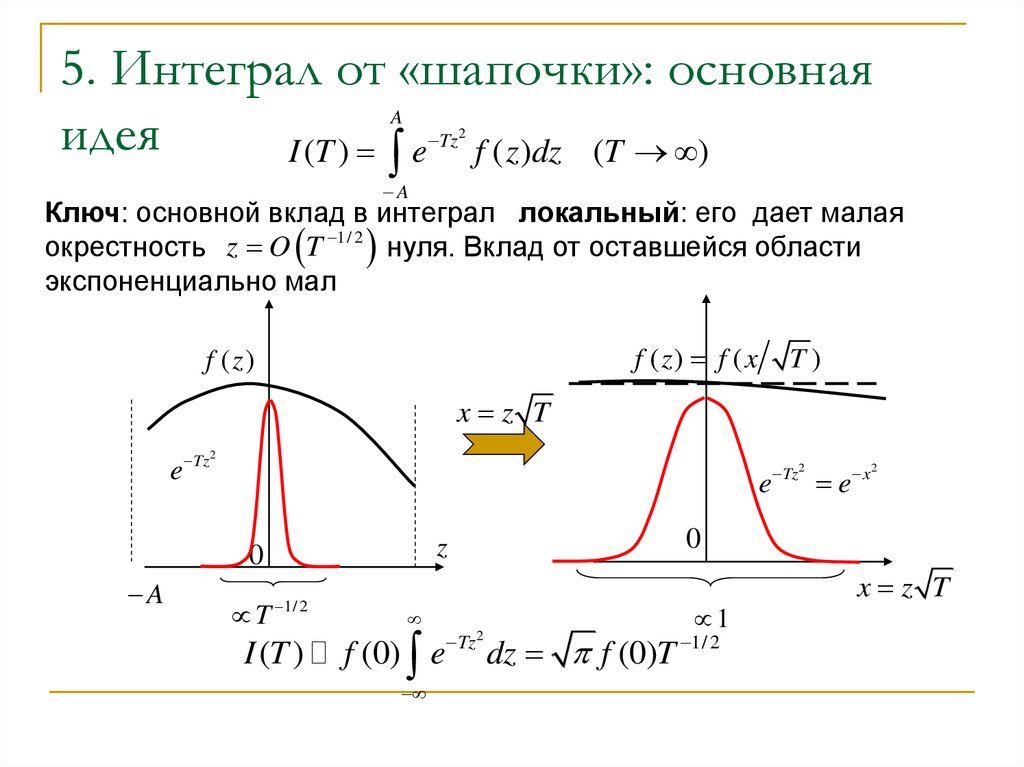
6. 5. Интеграл от «шапочки»: основная идея

I (T ) e f ( z )dz (T )
A
Tz 2
A
Ключ: основной вклад в интеграл локальный: его дает малая
окрестность z O T 1/ 2 нуля. Вклад от оставшейся области
экспоненциально мал
f ( z) f ( x
f ( z)
T)
x z T
e
Tz 2
e
A
T
1/ 2
I (T )
f (0) e
Tz 2
e
x2
0
z
0
Tz 2
dz f (0)T
1
1/ 2
x z T

7. 6. Интеграл от «шапочки»: вычисления

A
I (T )
e
Tz 2
f ( z )dz (T )
A
A
e
Tz
2
A
f ( z )dz T
1/ 2
A T
e
x2
f ( x / T 1/ 2 )dx
A T
2
1
T 1/ 2 e x f 0 xT 1/ 2 f 0 x 2T 1 f 0
2
dx
2
2
1
1/ 2
x
1/ 2
x
1
2 x2
T
f 0 xe dx T f x e dx
f 0 e dx T
2
0
2
f 0
2
f
O
T
0
T
4T

8. 7. Обобщение: Метод Лапласа

A
I (T )
Tg ( z )
e
f ( z )dz (T )
A
Пусть min g ( z ) g ( z0 )
Тогда основной вклад в интеграл дает малая окрестность точки z0
I
1
2
f ( z ) f ( z0 )
g ( z ) g ( z0 ) g ( z 0 ) z z 0
2
A
g0
2
exp
T
g
z
z
z z0 T y
0
f 0dz
A 0 2
A t0 T
g0 2
Tg0 1/ 2
f 0e T
exp 2 y dy
A t0 T
g
f 0e Tg0T 1/ 2 exp 0 y 2 dy
2
f ( z0 )e Tg ( z0 )
2
Tg ( z0 )
(T )

9. 8. Пример. Формула Стирлинга

z ln t t 0
0
0
z ! t z e t dt e z ln t t dt
t z
t z z1/ 2
z
нахождение точки максимума
перенормировка
z ln t t z ln z z z ln 1 z 1/ 2 z1/ 2 разложение по малым z 1/ 2
z ln z z 12 2 13 z 1/ 2 3 14 z 1 4
' '
1
2
1
z ! e z ln z z e 2 1 13 z 1/ 2 3 14 z 1 4 13 z 1/ 2 3
2
' '
z
z
1
2
e
z
2 1
1
12
1
z
2
1/ 2
z d
Относительная погрешность <0.001 уже
при z=1
Представленный пример является обобщением стандартного
метода Лапласа: здесь точка минимума не оставалась
неподвижной, но двигалась вдоль оси t с изменением z .

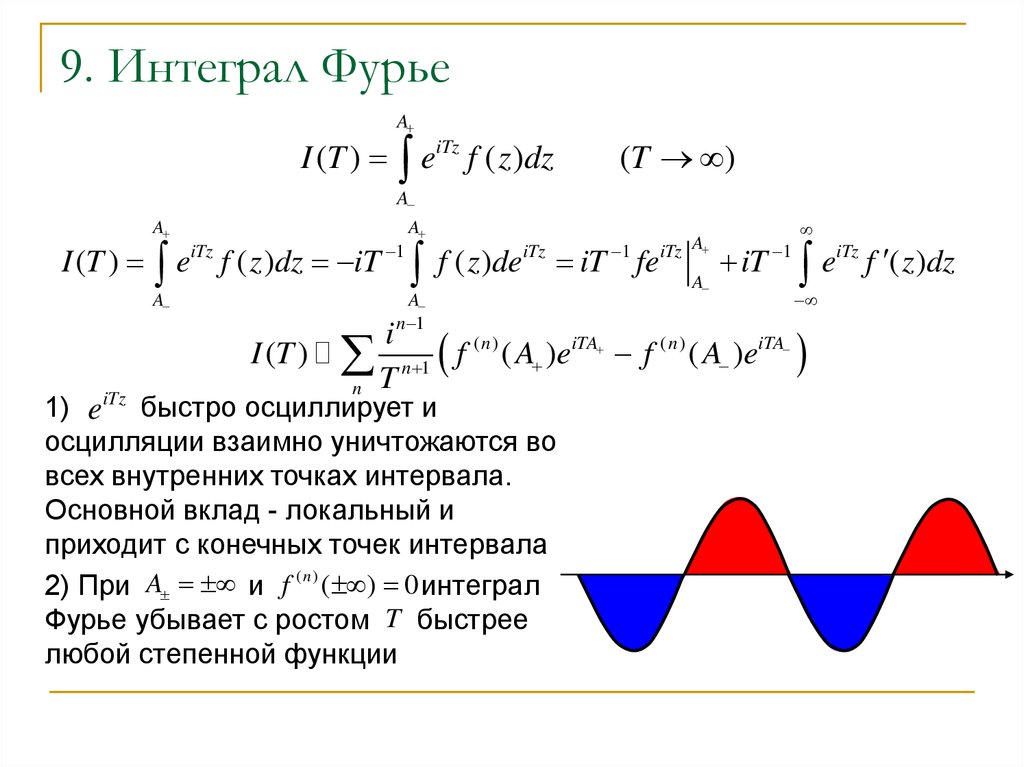
10. 9. Интеграл Фурье

I (T )
A
iTz
e
f ( z)dz
(T )
A
I (T )
A
A
A
A
n 1
iTz
1
iTz
1
e
f
(
z
)
dz
iT
f
(
z
)
de
iT
fe
I (T )
iTz A
A
iT 1 eiTz f ( z )dz
i
iTA
iTA
(n)
(n)
f
(
A
)
e
f
(
A
)
e
n T n 1
1) e iTz быстро осциллирует и
осцилляции взаимно уничтожаются во
всех внутренних точках интервала.
Основной вклад - локальный и
приходит с конечных точек интервала
2) При A и f ( n ) ( ) 0 интеграл
Фурье убывает с ростом T быстрее
любой степенной функции

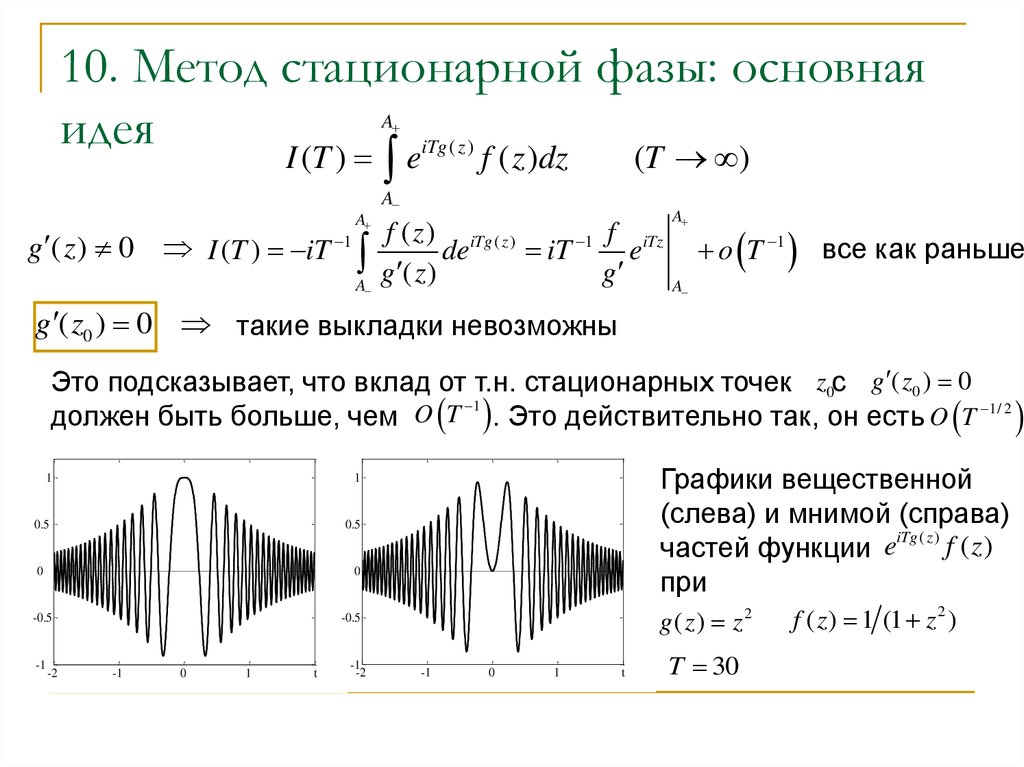
11. 10. Метод стационарной фазы: основная идея

I (T ) e
f ( z )dz
(T )
A
iTg ( z )
A
A
g ( z ) 0 I (T ) iT 1
A
f ( z ) iTg ( z )
f
de
iT 1 eiTz
g ( z )
g
A
o T 1 все как раньше
A
g ( z0 ) 0 такие выкладки невозможны
Это подсказывает, что вклад от т.н. стационарных точек z0с g ( z0 ) 0
1
должен быть больше, чем O T . Это действительно так, он есть O T 1/ 2
1
1
0.5
0.5
0
0
-2
g( z) z 2
-0.5
-0.5
-1
Графики вещественной
(слева) и мнимой (справа)
iTg ( z )
f ( z)
частей функции e
при
-1
0
1
t
-1
-2
-1
0
1
t
T 30
f ( z ) 1 (1 z 2 )

12. 11. Метод стационарной фазы: вычисления

I (T )
iTg ( z )
e
f ( z )dz (T )
g ( z0 ) 0 Основной вклад в интеграл дает малая окрестность точки z0
I (T )
g ( z0 )
2
exp iT g ( z0 ) 2 z z0 f ( z0 )dz
e
iTg ( z0 )
2
f ( z0 )
T g ( z0 )
e
Знак совпадает со знаком g ( z0 )
e
ix 2
dx
iTg ( z0 ) i / 4
2
f ( z0 )
T g ( z0 )

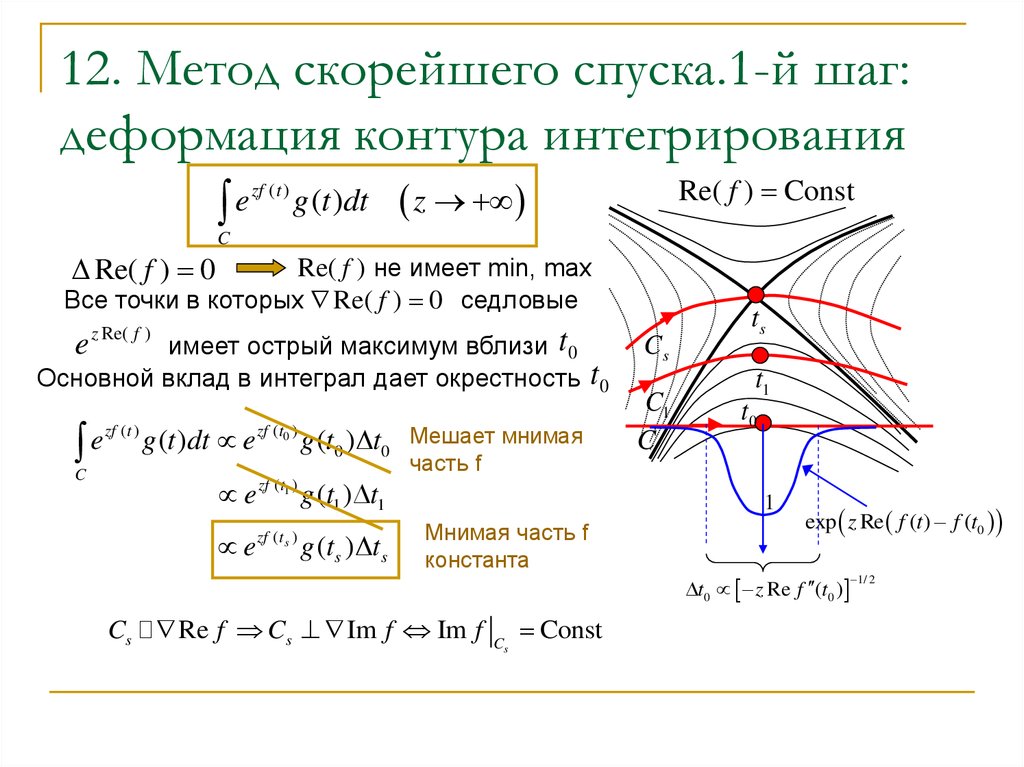
13. 12. Метод скорейшего спуска.1-й шаг: деформация контура интегрирования

zf ( t )
e
g (t )dt
Re( f ) Const
z
C
Re( f ) 0
Re( f ) не имеет min, max
Все точки в которых Re( f ) 0 седловые
z Re( f )
имеет острый максимум вблизи t 0
Основной вклад в интеграл дает окрестность
e
e
C
zf ( t )
g (t )dt e
zf ( t0 )
g (t0 ) t0 Мешает мнимая
e zf (t1 ) g (t1 ) t1
e
zf ( ts )
t0
g (ts ) ts
часть f
Cs
C1
C
ts
t1
t0
1
Мнимая часть f
константа
Cs Re f Cs Im f Im f
Cs
Const
exp z Re f (t ) f (t0
t0 z Re f (t0 )
1/ 2

14. 13. Метод скорейшего спуска.2-й шаг: локальный анализ

zf ( t )
e
g (t )dt
z
C
f (ts ) 0, f (ts ) 0
zf (t ) zf (ts )
1
1
2
3
zf (ts ) t ts zf (ts ) t t s
2
6
Вдоль выбранного пути интегрирования
t z 1/ 2
Перенормировка
Re zf (ts ) t ts 0
2
1
f (ts ) 2 O( z 1/ 2 )
2
g (t ) g (ts ) O( z 1/ 2 )
zf (t ) zf (ts )
e
Cs
' '
zf ( t )
g (t )dt
' '
e
1
f ( ts ) 2
zf ( ts ) 2
e
g (ts ) 1 O( z 1/ 2 ) z 1/ 2 d
1/ 2
2
e zf (ts ) g (ts )
zf
(
t
)
s
1 O( z
1/ 2
)

15. 14. Метод скорейшего спуска: резюме

zf ( t )
e
g (t )dt
z
C
Не меняя значения интеграла так изменяем контур интегрирования,
чтобы он проходил через одну или несколько точек перевала и
лежал бы в долинах ниже этих точек. Если ts - самая высокая точка
перевала, такая, в которой Re f имеет наибольшее значение, то ее
окрестность порождает главную часть интеграла при z .
Соответствующий вклад определяется формулой
1/ 2
2
e zf ( ts ) g (ts )
zf
(
t
)
s
Если имеется несколько точек перевала одинаковой высоты, то
вклад каждой из них имеет величину одного и того же порядка, и мы
должны просто просуммировать все эти вклады

16. 15. Пример: функция Эйри

1
xt 13 t 3
Ai( x )
e
dt
2 i C
x
Контур С, начинается на бесконечности с arg t 2 / 3 и
заканчивается на бесконечности с arg t 2 / 3
Точки перевала
t x1/ 2
4
Контур интегрирования должно продеформировать так, чтобы он проходил через
левую точку перевала
Вблизи нее:
1 3
2 3/ 2
1/ 2
1/ 2 2
1/ 2 3
xt t x x t x O t x
3
3
Ширина интервала, вносящего основной
1/ 4
вклад в интеграл есть величина порядка x
2
C
0
-2
-4
-4
-2
0
2
4
Линии уровня Re(g) при x=4 .
Более насыщенный цвет
линий отвечает меньшим
значениям функции

17. 16. Пример: функция Эйри

1
xt 13 t 3
Ai( x )
e
dt
2 i C
x
Перенормировка t x1/ 2 x 1/ 4
1
2
1
xt t 3 x 2 / 3 2 x 3/ 4 3
3
3
3
23 x 3/ 2
' i '
2
e
1
x 1/ 4 e exp x 3/ 4 3 d
2 i
3
' i '
4
g(x,t) в новых переменных
Ai( x )
2 x 3/ 2
' i '
e 3
1 3/ 4 3 1 3/ 2 6
1/ 4
2
x
e 1 x x
2 i
18
3
' i '
23 x 3/ 2
5 3/ 2
1
x
1/ 2 1/ 4
2 x 48
e
d
2
C
0
-2
-4
-4
-2
0
2
4

18. 17. Упражнения к лекции 3

1.
En ( x) t e dt,
(a, x) t a 1e t dt
n xt
1
2.
x
Получить главный член асимптотического представления
интеграла при x
I ( x)
3.
x интегралов
Найти асимптотическое разложение при
ixt 2
e
1 t 2 dt
Найти асимптотическое поведение интеграла при
z O 1
1
K x ( z ) e xt z ch t dt
2
x и