mathematicsSimilar presentations:
Основы преобразования Чебышева -GDCT
1. Основы преобразования Чебышева -GDCT
2. Интегральное преобразование блока
s(x,y)= u(x, y)I (x, y){x,y}
mk(x,y)= m(x) k(y). , z1=x/ax, z2=y/ay,
,
s(x, y) Cmk p m (x / a x )p k (y / a y )
m,k
Cmk (d md k ) 1 (z1)p m (z1)dz1 s(a x z1,a yz 2 ) (z 2 )p k (z 2 )dz 2.
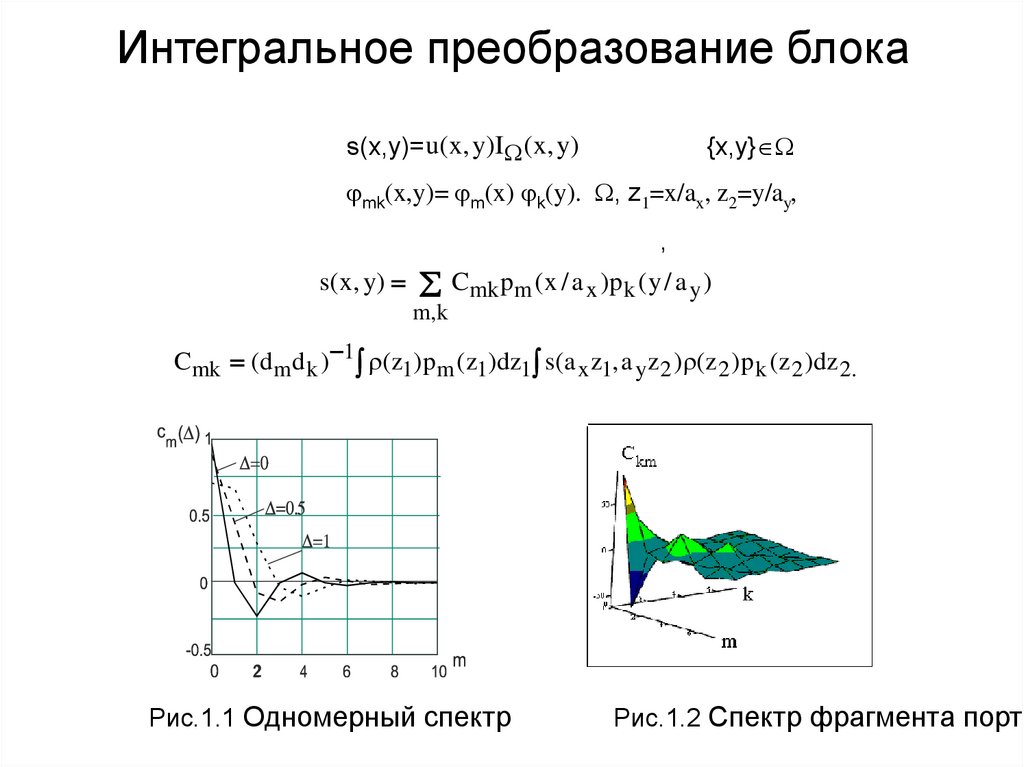
Рис.1.1 Одномерный спектр
Рис.1.2 Спектр фрагмента портр
3.
Одномерный алгоритм преобразования Чебышева.1 1 s(z)Tm (z)
N 1
dz
s(z n )Tm (z n ) .
2
d m 1 1 z
dm N n 0
Cm
2 N 1
n 0.5
s(z
)cos(
m
), C0
n
N n 0
N
1 N 1
s(z n )
N n 0
2 M
2 M
SM (z) g m
CmTm z g m
Cm cos(m arccos(z))
N m 0
N m 0
m=0.
dm= /2, m 0, dm= , m=0
g m 1 m>0; gm 0.5
Tm(zn)=cos(m arccos(zn))=cos( m(n+0.5)/N),
Применение квадратурных формул Гауссовского типа (наивысшей
точности)
Неравномерное расположение отсчетов zn=cos( (2n+1)/2N) –нули
TN(z);
Наивысшая скорость сходимости рядов Чебышева
Восстановление изображения в произвольной точке Z [-1,1]
Субпиксельный сдвиг и масштабирование восстановленного
изображения
4.
Двумерный алгоритм преобразования (GDCT).SK(N1 N1) S(N N) C(M M) R(L L)
x n ROUND(0.5 (N1 1) (1 cos( (n 0.5) / N)))
yk ROUND 0.5 (N1 1) (1 cos (k 0.5) / N )
S snk s(x n , yk ) .
C C m,l S T ,
(N M) .
C(M M).
m,n (n)
NM
g m cos m arccos(z j )
R TC .
(L M).
R(L L).
0.5
2
(n
0.5)
,
N cos( m
N
LM gm cos(m arccos( L2j 1 1 ))
.