Случайные события и величины

1. Теория вероятностей и математическая статистика физический факультет 2018-2019 уч.год

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
2018-2019 УЧ.ГОД
ТЮРНЕВА Т.Г., ДОЦЕНТ
КАФЕДРА ТЕОРИИ ВЕРОЯТНОСТЕЙ И ДИСКРЕТНОЙ МАТЕМАТИКИ ИМЭИ ИГУ

2.

2
Теория вероятностей
Математическая статистика

3. Образовательный портал ИГУ

3
ОБРАЗОВАТЕЛЬНЫЙ ПОРТАЛ ИГУ
• Запись на курс Теория вероятностей и математическая
статистика

4. Теория вероятностей и математическая статистика

4
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
• 1. Элементы комбинаторики
• 2. Случайные события
25 задач +защита решения
• 3. Случайные величины
Контрольная работа
Семестровое задание
• Одномерные с.в.
• Многомерные с.в.
• 4. Предельные теоремы т.в.
Домашняя контрольная работа
Домашняя исследовательская
работа
• 5. Элементы математической статистики

5. Случайные события и величины

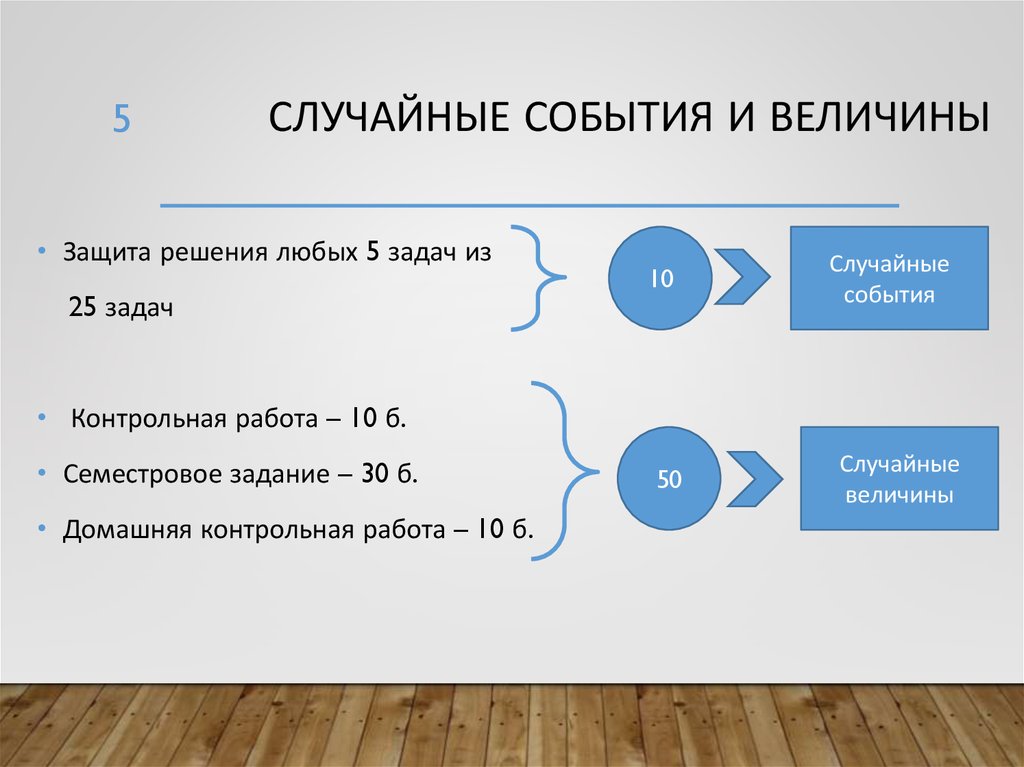
5
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕЛИЧИНЫ
• Защита решения любых 5 задач из
25 задач
10
Случайные
события
• Контрольная работа – 10 б.
• Семестровое задание – 30 б.
• Домашняя контрольная работа – 10 б.
50
Случайные
величины

6. зачет БРС

6
60 +
10+50
ЗАЧЕТ
БРС
30 +
10 – презентация
20 – домашняя
иссл. работа
10 =100
Олимпиада по
т.в

7.

Характеристики основных вероятностных распределений. Моделирование распределений
случайных величин.
7
1. Изучить основные свойства, характеристики и зависимость от параметров следующих
распределений:
1. биномиального, 2. пуассоновского, 3. геометрического, 4. равномерного, 5. показательного, 6.
нормального, 7. хи-квадрат, 8. Стьюдента, 9. Фишера.
Для каждого из распределений дать определение математической или физической модели,
указать область, где оно встречается и используется.
Записать функцию распределения, ряд распределения или плотность распределения, параметры,
математическое ожидание, дисперсию, описать особенности формы распределения и
асимптотические свойства.
Для своего варианта V, где V-номер студента в списке группы, определить параметры
распределений случайных величин.
Функция V mod a равна остатку от деления числа V на а.
2. Выполнить следующие расчеты:
1. Для каждого из распределений определить точные значения математического ожидания и
дисперсии.
2. Для непрерывных распределений вычислить значения квантилей
порядков 0, 25; 0,5.
3. Вычислить и показать на графиках плотности распределений 4, 5, 6 соответствующие
вероятности