Решение задач по геометрии

1. Использование формул.

Формула площади правильного многоугольника:
p2
1 2
360°
S n = R × n sin
2
n
2009. В-1. №18.Площадь круга, описанного около
шестиугольника равна 36 кв.см. Найти площадь
правильного шестиугольника.

2.

A)66
3.
B )48
3.
C )54
3.
D )72
3.
E )56
3.
p R = 36p .
2
Значит R=6. Итак,
1 2
360° 1 2
360° 1
3
S6 = R × n sin
= 6 × 6 × sin
= × 36 × 6 × sin 60° = 108 × = 54 3.
2
n 2
6 2
2
Правильный ответ С.

3.

2009. В-14. №25. Высота правильного тетраэдра
равна h. Вычислить его полную поверхность
Использование формулы площади правильного треугольника:
и формулы радиуса окружности, описанной около
2
треугольника:
a 3
S=
4
a
R=
.
3

4.

a2 3 2
S = 4 SV = 4 ×
= a 3.
4
Зная, что боковое ребро правильной пирамиды проектируется на радиус описанной
около правильного треугольника окружности, и, что боковое ребро, высота пирамиды
и радиус описанной окружности образуют прямоугольный треугольник, по теореме
Пифагора имеем:
a 2 = h2 + (
a 2
) .
3
a2
a = h2 .
3
2 2
a = h2 .
3
3
a 2 = h2
2
A)h
2
S ï î ëí = a
2
3h 2 3
3=
.
2
2
h2 2
3h 2 3
5h 2 3
h2 3
3.B)
.C )
.D )
.E )
.
3
2
3
4
Правильный ответ С.

5.

Использование теоремы Виета.
2009. В-12. №4. Найдите сумму корней уравнения:
3 x + 5 x - 8 = 0.
2
А)8. В)-8.
С)5.
5
D) 3 .
E) 3.
Разделим обе части уравнения на 3, получим
5
8
x + x- =0
3
3
2
5
x1 + x2 = - .
3

6.

6.
В условиях тестирования важно использовать свойства, позволяющие
быстрее исследовать функцию на четность, нечетность (не пользуясь
определением)
1.Сумма четных функций - функция четная.
2.Сумма нечетных функций - функция нечетная.
3.Произведение четных функций- функция четная.
4.Произведение двух нечетных функций
- функция четная.
1
5.Произведение четной и нечетной функций
- функция нечетная.
f
6.Если функция f четная(нечетная), то четная (нечетная).
1
f

7. 2009. В-23. №7.Какая из функций в области определения является четной?

A) y = 9 - x 2 + x 2 .B) y = 9 - x 2 + x 3.C ) y = 9 - x 2 + x 9 .D) y = 9 - x 2 + x 7 .E ) y = 9 - x 2 + x 5 .
Ответ находится быстро, если использовать свойство
1.у=четная+четная=четная функция.
2009. В-25. №15.Какая из функций является четной?
A) y =
1
1
1
1
1
1
1
1
1
1
+
.
B
)
y
=
+
.
C
)
y
=
+
.
D
)
y
=
+
.
E
)
y
=
+
.
2
7
2
4
2
3
2
2
5
1+ x 1+ x
1+ x 1+ x
1+ x 1+ x
1+ x 1+ x
1+ x 1+ x
Используя свойства 1 и 6 получаем правильный ответ В.

8. Рассмотрим некоторые тестовые задания по математике, предлагавшиеся на ЕНТ. Для решения этих заданий не потребуется никаких вычислений, а

Рассмотрим некоторые тестовые задания по
математике, предлагавшиеся на ЕНТ. Для
решения этих заданий не потребуется никаких
вычислений, а ответ находится сам собой, почти
автоматически без серьезных усилий со стороны
решающего.

9. Смотри в ответ!  

Смотри в ответ!
2008.В-18,№25.Диагонали трех граней прямоугольного
параллелепипеда, сходящиеся в одной вершине,
a,b,c.Найти линейные размеры паралллелепипеда.

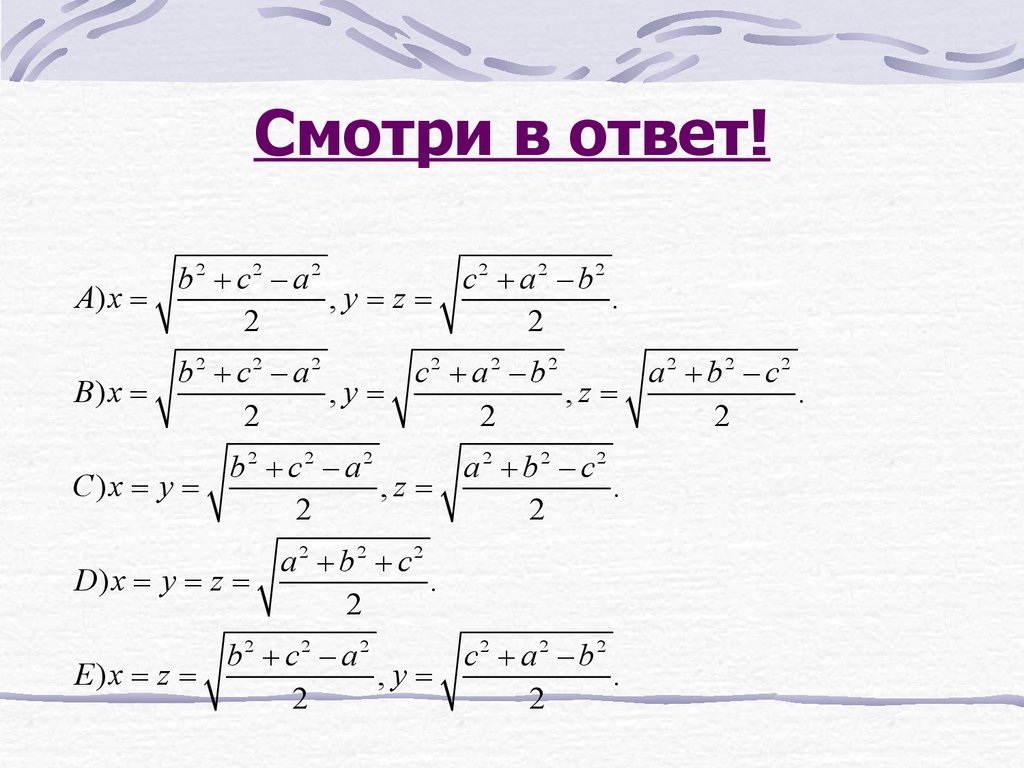
10. Смотри в ответ!  

Смотри в ответ!
A) x =
b2 + c2 - a2
,y= z =
2
B) x =
b2 + c2 - a2
,y=
2
C)x = y =
E)x = z =
c2 + a 2 - b2
,z =
2
b2 + c 2 - a 2
,z =
2
D) x = y = z =
c 2 + a 2 - b2
.
2
a 2 + b2 - c2
.
2
a2 + b2 + c2
.
2
b2 + c2 - a 2
,y=
2
c2 + a2 - b2
.
2
a 2 + b2 - c 2
.
2

11. 2009. В-16. №1.

Периметр прямоугольника 84 см. Найти длину и ширину
прямоугольника, если ширина относится к длине как 2:5.
Смотрим в ответы.
А) 10см;32 см.В) 14см; 28см.С) 12см; 30см. D) 13см; 29см.
Е)11см; 31см.
Первому условию удовлетворяют все ответы, проверяем
выполнение второго условия: отношение ширины к длине равно
2:5, только ответ С удовлетворяет этому условию 12:30=2:5.
.

12. 2009. В-16. №1.

Одно число меньше другого на 5. Разность между
квадратами меньшего и большего числа равна 85.
Найти эти числа.
А)-12 и 8.
В)-3 и 7.
С)-6 и -11.
D)15 и 7.
Е) 6 и 11
Ответ:С.

13.

Средняя линия трапеции равна 7 см. Одно из ее
оснований больше другого на 4 см. Найти основания
трапеции.
А) 10 см, 4 см
2 см, 12 см.
В) 5 см, 6 см
C) 5 см, 9 см
D) 11 см, 3 см
Е)
Прежде всего, в глаза бросается, что ответ В) неверен, так как в
трапеции с основаниями 5 см и 6 см средняя линия не равна 7 см.
Однако эта попытка решения весьма слабая и не приводит сразу к
ответу. Лучше не спешить и обратить внимание на то, что одно из
оснований трапеции должно быть больше другого на 4 см и тогда ответ
С) находится однозначно и мгновенно.

14. . Две трубы вместе наполняют бассейн за 6 часов. Определите, за сколько часов наполняет бассейн каждая труба в отдельности, если известно, чт

. Две трубы вместе наполняют
бассейн за 6 часов. Определите, за
сколько часов наполняет бассейн
каждая труба в отдельности, если
известно, что из первой трубы в
час вытекает на 50 % больше
воды, чем из второй.

15.

А) 10 ч, 20 ч
В) 15 ч, 10 ч
Е) 18 ч, 23 ч.
C) 30 ч, 15 ч
D) 25 ч, 20 ч
Иногда можно зацепиться за такое условие, которое
позволит однозначно найти правильный ответ.
Таким условием является то, что если время,
необходимое для работы медленного насоса,
увеличить на его половину, то получим время
работы более производительного насоса. Такому
условию удовлетворяет только ответ В).

16.

Найдите три числа, из которых второе больше первого
настолько насколько третье больше второго, если известно, что
произведение двух меньших чисел равно 85, а произведение
больших равно 115.
А) 8,5; 9; 12
В) 9,1; 3; 4
C) 5; 7; 9
D) 8,5; 10; 11,5
Е) 12; 11; 10.
Удобнее всего в этом задании вычислить произведения двух
меньших чисел в каждом из приведенных ответов. Это
произведение будет равно 85 только в ответе D). Ответ D)
удовлетворяет также остальным двум условиям задания.

17.

Разложите квадратный трехчлен на
множители
2x + 7 x - 4
2
А) 2(х - 2)(х+3).
В)2(х - 1/2)(х + 4)
C) -2(х - 1/2)(x + 1/34)
D) -2(x + 3)(x + 4)
Е) 2(x + 0,5)(x - 4).
Правильный ответ:В.

18.

Решите уравнение;
1+ x
10
А) 1; 3
D) 10; 2
2
1- x
- 10
В) -1; 3
Е) -1/10; 1.
2
= 99
C) -1; 1

19. Угадывание ответа.

2009.В-1. №5.Упростите выражение:
2
3
2
a
a
a
a
(
- 2
):(
).
2
2
a + b a + 2ab + b
a + b (a + b )
Пусть а=1, в=1, тогда
1
1
1
1
( - ) : ( - ) = 1.
2
4
2
4
a -b
b-a
a
A)a.B )a + b.C )
.D )
.E )
.
2
2
( a + b)
a+b
(a + b)

20.

2005. В-10.№13. Сократить дробь:
x14 - x 7 + 1
.
21
x +1
1
x +1
1
3x
x +1
A) 7
.B ) 7
.C ) 7
.D ) 7
.E ) 7
x +1
x +1
x -1
x +1
x
Если х=0. то значение дроби равно 1. Этому значению
соответствуют ответы А и В. пусть х=1, получим:
114 - 17 + 1 1
= .
21
1 +1
2
Этому значению соответствует ответ под буквой А. Значит
правильный ответ А.

21.

2007. В-28. №10. Сократить дробь:
p - 125
2
p + 5 p + 25
3
Пусть p=0, тогда
0 - 125
= -5
2
0 + 5 × 0 + 25
3
при р=0, 0-5 =-5.Значит ответ С.
А) р+1
В) р+5
С) р-5
p
D) 5
Е) 5р.

22. Упрощение стандартных тригонометрических выражений.

2009.В-10. №20. Упростить выражение:
2(sin 4 x + sin 2 x cos 2 x + cos 4 x) 2 - sin 8 x - cos8 x.
Пусть х=0, тогда:
2(sin 4 0 + sin 2 0cos 2 0 + cos 4 0) 2 - sin 8 0 - cos8 0 = 2(0 + 0 + 1) 2 - 0 - 1 = 2 - 1 = 1.
A) - 1.
1
B)
.
2
C )1.
1
.
4
E )2.
D)
Ясно, что ответ С.

23.

2009. В-11. №14. Упростить выражение:
1 - 2sin a cos a
+ cos a .
sin a - cos a
a = 180°
1 - 2sin180° cos180°
1- 0
+ cos180° =
- 1 = 1 - 1 = 0.
sin180° - cos180°
0 +1
что удовлетворяет ответу А.
A)sin a .B)1.C ) cos a .D) - cos a .E ) - sin a .

24.

2004. В-32. №10. Упростить выражение:
2 cos
2
a
А) 0,5. В) -1.
2
- cos a .
С) 1.
D) 2.
a =0
0
2 cos - cos 0 = 2 - 1 = 1.
2
2
Это соответствует ответу под буквой С.
Е) 0.

25.

2009. В-13. №23. Упростите:
cos 4a + 4 cos 2a + 3.
A)8cos a .B )6 cos a .C )8sin a .D)8tg a .E )6sin a .
4
4
a =0
4
4
4
cos 4 × 0 + 4 cos 2 × 0 + 3 = 1 + 4 + 3 = 8.
правильный ответ А.

26. 2009. В-18. №22. Упростить выражение:

ctga + tga
. a = 60°
ctga - tga
1
+
ctg 60° + tg 60°
= 3
1
ctg 60° - tg 60°
3
1
A) .
cos 2a
B ) sin a .
1
C)
.
cos 2a
D ) - 1.
E )1
1+ 3
4
3
=
=
= -2.
1 - 3 -2
3
3
3
Полученному значению удовлетворяет ответ С.
1
1
1
=
=
= -2.
cos 2 × 60° cos120° - 1
2

27. 2009. В-20. №22.Упростить выражение:

sin a - tg a
.
2
2
cos a - ctg a
2
2
a = 60°
3 2
3
3 - 12
9
2
)
(
3)
3
sin 2 60° - tg 2 60°
= 2
= 4
= 4 = 4 = 27.
2
2
1
1 2
1 1
3-4
1
cos 60° - ctg 60°
( )2 - (
)
2
4 3
12
12
3
(
A)tg 2a .
B )tg a .
3
a = 60°
правильный ответ под буквой С.
C )tg 6a .
D )ctg 2a .
E )ctg 6a .
tg 6 60° = (tg 60°) 6 = ( 3) 6 = 27.

28. 2009. В-21. №22. Упростите:

cos (a + b ) + cos (a - b ) - cos 2a cos 2 b .
A)cos a .
a =b =0
B)1.
cos (0 + 0) + cos (0 - 0) - cos 2 × 0 cos 2 × 0 = 1 + 1 - 1 = 1.
C )0.
что соответствует ответу В.
D) - 1.
E )sin a .
2
2
2
2

29. 2009. В-22. № 21. Упростите:

2
sin (
a
2
+ 2 b ) - sin (
2
a
2
- 2 b ).
Выше указанным методом невозможно найти правильный ответ, надо
применить формулу понижения степени:
1 - cos a
sin
=
2
2
2
a
Ответ получится под буквой С.
sin a sin 4 b

30. 2009. В-25. №21.Упростите:

2 - sin a - cos a
.
sin a - cos a
a =0
2 - sin 0 - cos 0
=
sin 0 - cos 0
2 -1
= 1-1
2.
Посмотрим в ответы:
a p
a
a p
a p
A)tg ( - ).B)tg .C )tga .D) sin( - ).E ) cos( - ).
2 8
2
2 8
2 8

31.

p
2
1 - cos
10 p
p
p
2- 2
4
2
tg ( - ) = tg (- ) = -tg = ===
p
2 8
8
8
2
2
sin
4
2
2 2 - 2 2( 2 - 1)
=== -( 2 - 1) = 1 - 2.
2
2
Правильный ответ А.

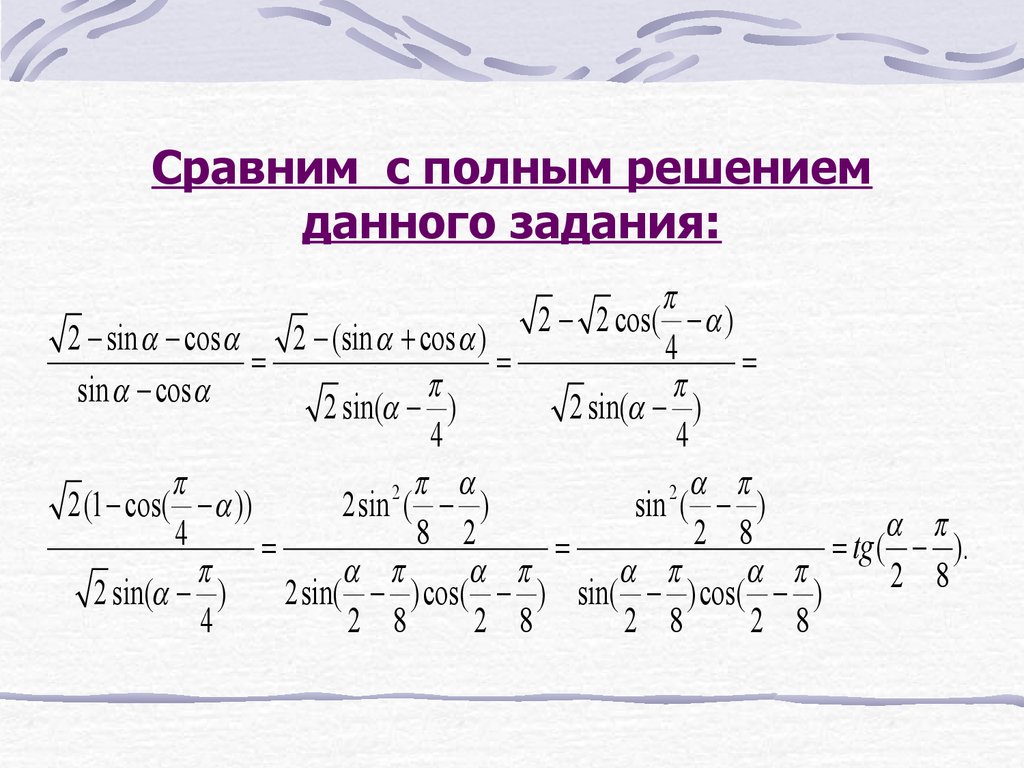
32. Сравним с полным решением данного задания:

p
2 - 2 cos( - a )
2 - sin a - cos a 2 - (sin a + cos a )
4
=
=
=
p
p
sin a - cos a
2 sin(a - )
2 sin(a - )
4
4
p
2 p a
2 a p
2sin ( - )
sin ( - )
2(1 - cos( - a ))
a p
8
2
2
8
4
=
=
= tg ( - ).
p
a p
a p
a p
a p
2 8
2 sin(a - )
2sin( - )cos( - ) sin( - )cos( - )
4
2 8
2 8
2 8
2 8

33. Применение формул тригонометрии.

2009.В-23. №22. Упростите:
sin(a - b ) + 2 cos a sin b
.
sin(a + b )
sin x
2009. В-24. №20. Выражение
1 + tg x
2
после упрощения равно:
A) sin x cos x .
B ) sin x cos x.
C ) sin x cos x .
D)
sin x
.
cos x
E ) sin x cos x.

34.

Метод угадывания ответа не годится, следует
1
2
1
+
tg
x
=
использовать формулу:
2
cos x
x2 = x .
sin x
sin x
sin x
=
=
= sin x × cos x
2
1
1
1 + tg x
2
2
cos x
cos x

35. Решение логарифмических уравнений. 2009. В-5. №12. Решить уравнение:

log
ОДЗ:
2
2
x - log 0,5
1
= 6.
x
x>0
A-0,25;8. B) -2;3.
C) -6;1.
D) 0,25;8.
Условию х>0 удовлетворяет ответ D.
E) 2;-3.

36. 0208.Решить уравнение:

2
x log x 27 × log 9 x = x + 4.
ОДЗ:
x > 0, x ¹ 1
4
A) - 2;
.
3
4
B) ; 2.
3
2
C) ;1.
3
D )2.
Удовлетворяет
E )1.
ОДЗ только ответ D.

37. Решение систем уравнений.

2009. В-3. №11. Решить систему уравнений:
ìlog 2 ( x + y ) = 4
í
î2 x - y = 5
А) (9;-7). В) (0;12). С) (7;9). D) (7;6). Е) (8;4).
Ответы А,В, D,Е не удовлетворяют уравнению 2,
значит правильный ответ С.

38. Дана система уравнений

3
ì 2
x + xy =
ï
4
ï
.
íx
3
ï +1 =
2
ï
îy
Найти ху.
Разделим почленно первое уравнение на второе:

39.

x( x + y ) 3 3
= :
x+ y 4 2
y
1
xy =
.
2
Легко и быстро получается решение
.

40.

Применение основного свойства дроби.
2009. В-5. №13.Вычислите:
sin a - 3cos a
, tga = 3.
2
2
2sin a + cos a
2
2
Разделим числитель и знаменатель дроби почленно на
cos a ¹ 0
2
sin 2 a 3cos 2 a
2
2
2
tg
a -3
9-3
6
cos a
cos a =
=
=
.
2
2
2
2 sin a cos a
2tg a + 1 18 + 1 19
+
2
cos a
cos 2 a
Правильный ответ С.

41.

Применение свойства равнобедренной
трапеции, диагонали которой взаимно
перпендикулярны.
Если в равнобедренной трапеции диагонали
взаимно перпендикулярны, то средняя линия
трапеции равна её высоте. Следовательно,
S =h
2

42.

Найти площадь равнобедренной трапеции, у
которой высота равна 10, а диагонали взаимно
перпендикулярны.
S = h = 10 = 100.
2
2

43.

Решение тригонометрических уравнений.
2009. В-2. №7.Решить уравнение:
tgx+ctgx=2
A) B)
p
4
C) ±
D)
p
4
p
4
+ 2p n, n Î Z .
+ 2p n, n Î Z .
p
4
+ p n, n Î Z .
+ p n, n Î Z .
. E) - p
4
+ p n, n Î Z .

44. Использование формулы квадрата двучлена.

2009. В-15. №20. Вычислить sin a cos a ,
1
sin a + cos a = .
3
возведем в квадрат обе части равенства:

45.

1 2
(sin a + cos a ) = ( ) ;
3
2
1
sin a + 2sin a cos a + cos a = ;
9
1
2sin a cos a = - 1;
9
8
2sin a cos a = - ;
9
4
sin a cos a = - .
9
2
2
Правильный ответ получен под буквой А.

46. Свойство медианы правильного треугольника.

2009. В-15. №18. В правильный треугольник
вписана окружность, радиус которой равен 5. тогда
медиана этого треугольника равна:
А) 5.
В) 10.
С) 25.
D) 15.
Е) 20.
r =
1
m
3
где, m-медиана
длина медианы равна трем радиусам вписанной в
правильный треугольник окружности, то есть 15. Ответ D.

47.

48. 2007. В-10.№30. Внутри острого угла, равного ,взята точка М, удаленная от его сторон на рсстояния k и n. Найти расстояние от вершины угла до точки М.

2007. В-10.№30.
Внутри острого угла, равного a,взята
точка М,
удаленная от его сторон на рсстояния
k и n. Найти расстояние от вершины
угла до точки М.
a

49.

A)
k 2 + n 2 + 2kn cos a
.
sin a
B)
k 2 + n 2 - 2kn cos a
.
sin a
C)
D)
E)
k 2 - n 2 - kn cos a
.
sin a
sin a
n 2 + k 2 - 2kn cos a
.
n 2 - k 2 - 2kn cos a
.
sin a

50.

ÐKMN = 180° - a .
DKMN
KN 2 = KM 2 + MN 2 - 2 KM × MN cos(180° - a ) = k 2 + n 2 + 2kn cos a .
Через точки А,К,М и N проведем окружность, АМ- диаметр. О- центр
вспомогательной окружности. Пусть ОК=ОN=R.
ÐKON = 2a
DKON
KN 2 = OK 2 + ON 2 - 2OK × ON cos ÐKON = R 2 + R 2 - 2 R 2 cos 2a = 2R 2 (1 - cos 2a ) = 4 R 2 sin 2 a .

51.

4 R sin a = k + n + 2kn cos a .
2
2
2
2
k + n + 2kn cos a
R=
.
2sin a
2
2
k + n + 2kn cos a
AM = 2 R =
.
sin a
2
2

52.

Формулы для вычисления длины
биссектрисы.
a
2bc cos
2.
la =
b+c
la = bc - b1 × c1.
la =
bc (b + c + a )(b + c - a )
.
b+c