Similar presentations:
Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью
1. Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью.
Издательство «Легион»Методы решения задач
повышенной сложности по
геометрии (ЕГЭ).
Семинар с практической частью.
Фридман Елена Михайловна
2. Основные методы решения геометрических задач
Метод дополнительных построенийМетод геометрических преобразований
Метод подобия
Метод площадей
Метод вспомогательной окружности
Метод геометрического видения
Метод координат
Векторный метод
3. Основные факторы успеха
• Время (чем больше времени наподготовку, тем лучше)
• Система (работа по плану, а не от
случая к случаю)
• Желание
подготовиться
4. Причины ошибок в решении геометрических задач
Незнание и/или непонимание аксиом,определений, теорем, а также методов решения
задач;
неумение их применять, (в том числе, применять
их неверно);
невнимательное чтение условия и вопроса
задания;
вычислительные ошибки;
нарушения логики в рассуждениях;
принятие ошибочных гипотез;
недостатки в работе с рисунком.
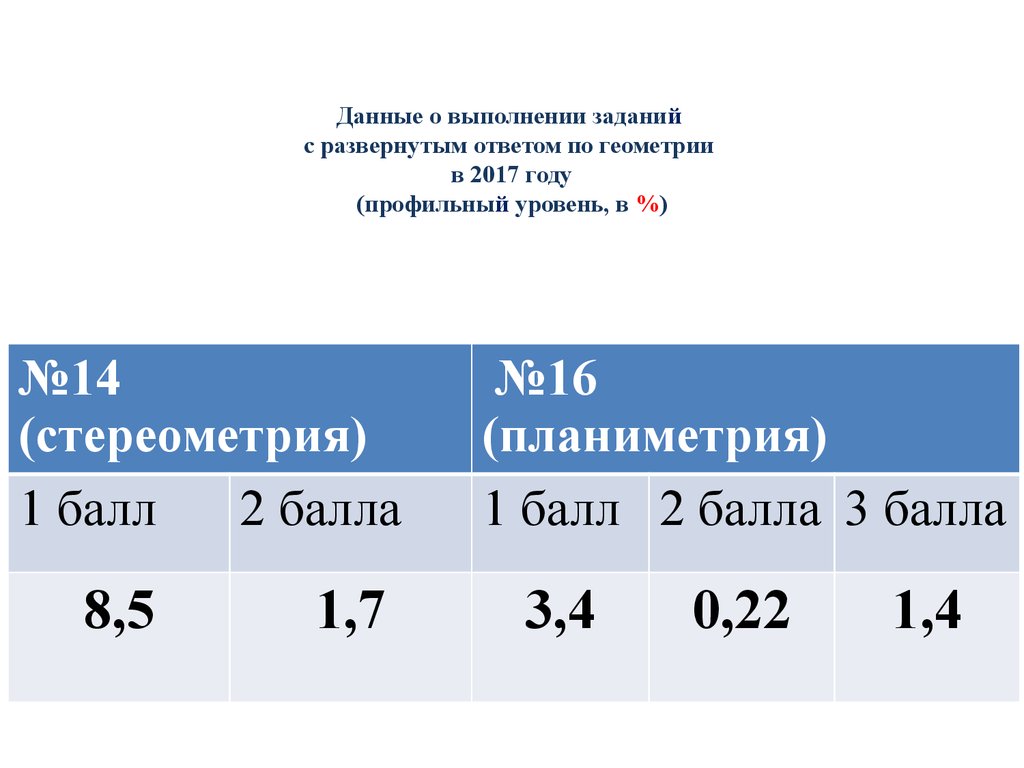
5. Данные о выполнении заданий с развернутым ответом по геометрии в 2017 году (профильный уровень, в %)
№14(стереометрия)
1 балл
2 балла
8,5
1,7
№16
(планиметрия)
1 балл 2 балла 3 балла
3,4
0,22
1,4
6.
7.
8.
9. Что нужно знать
Аксиомы и теоремы стереометрии ипланиметрии
Правила изображения (проектирования)
пространственных фигур на плоскость
Основные методы построения сечений
многогранников
10. Что нужно уметь
Применять знания в процессе решения задачи:• Увидеть, что нужно построить на каждом шаге
построения сечения
• Предложить способ построения
• Построить (точку, линию, плоскость и т.д.)
Veni, vidi, vici (пришел, увидел, победил)
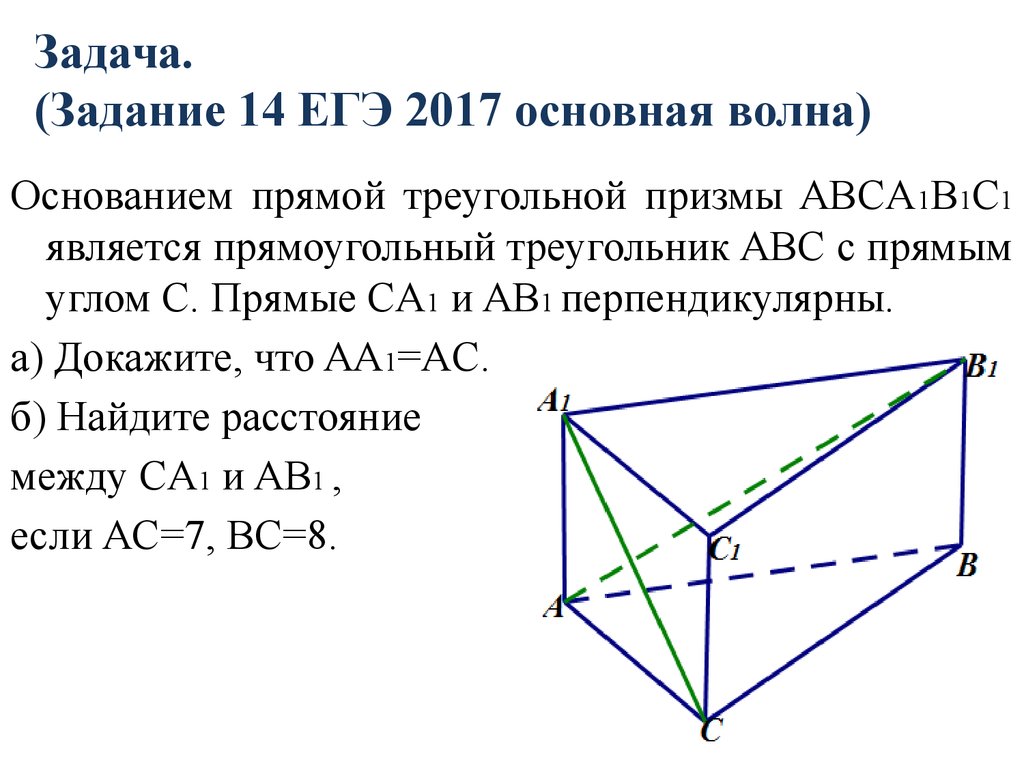
11. Задача. (Задание 14 ЕГЭ 2017 основная волна)
Основанием прямой треугольной призмы ABCA1B1C1является прямоугольный треугольник ABC с прямым
углом С. Прямые CA1 и AB1 перпендикулярны.
а) Докажите, что AA1=AC.
б) Найдите расстояние
между CA1 и AB1 ,
если AC=7, BC=8.
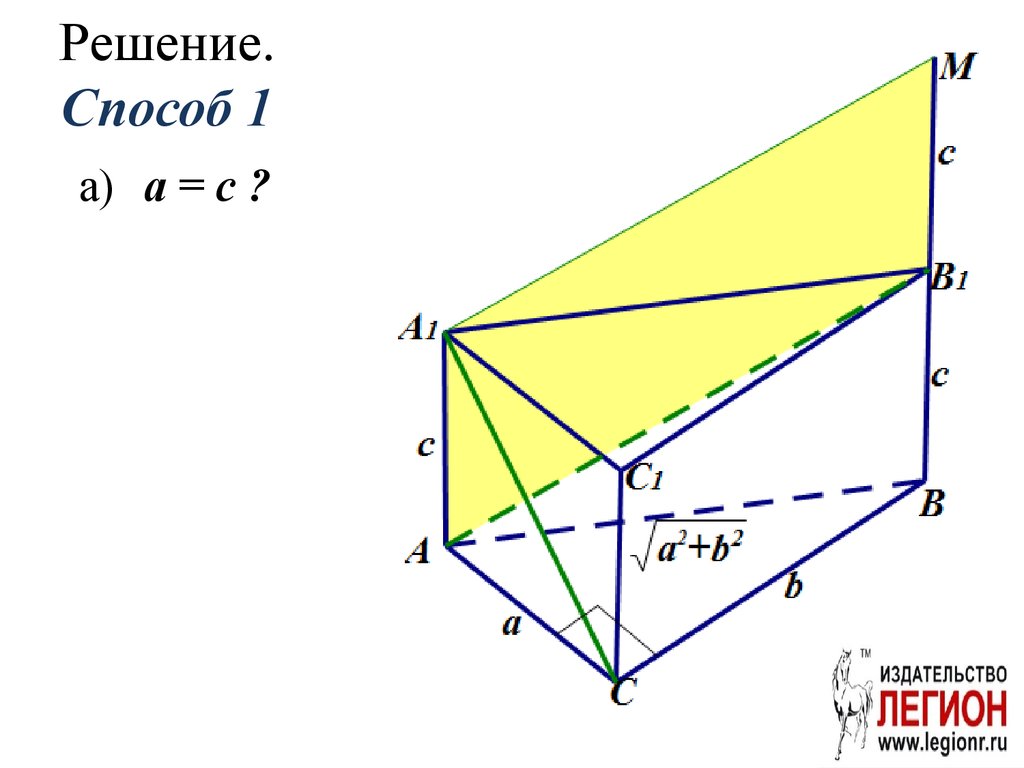
12. Решение. Способ 1
а) a = c ?13.
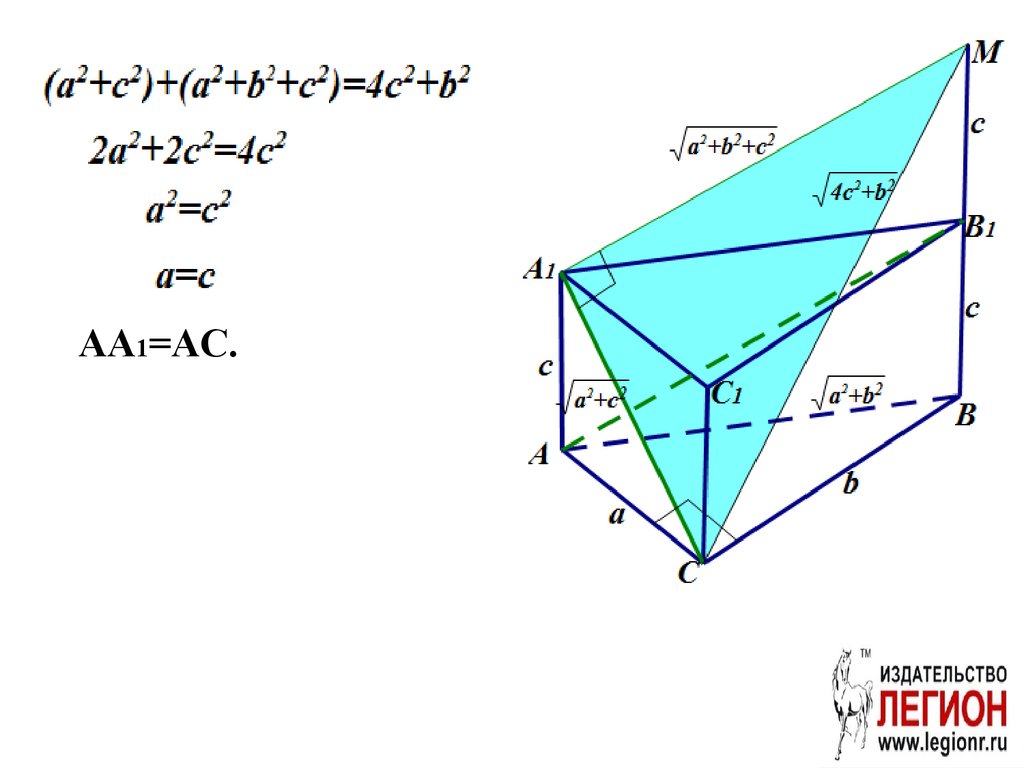
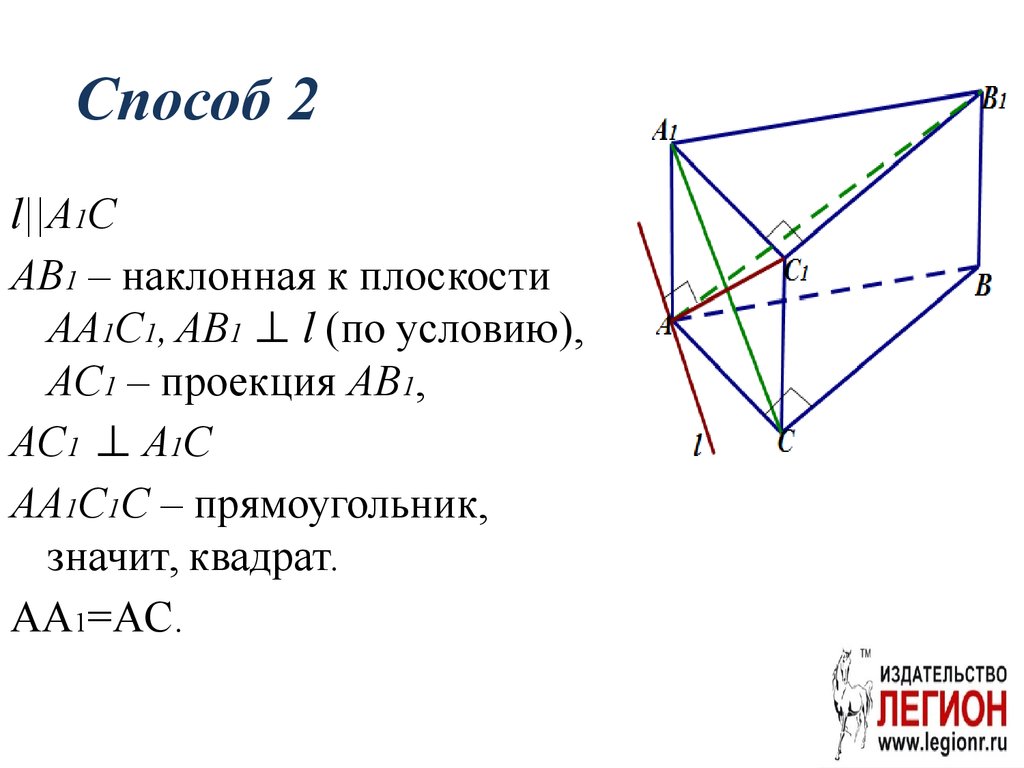
AA1=AC.14. Способ 2
l||A1CAB1 – наклонная к плоскости
AA1C1, AB1 ⊥ l (по условию),
AC1 – проекция AB1,
AC1 ⊥ A1C
AA1C1C – прямоугольник,
значит, квадрат.
AA1=AC.
15.
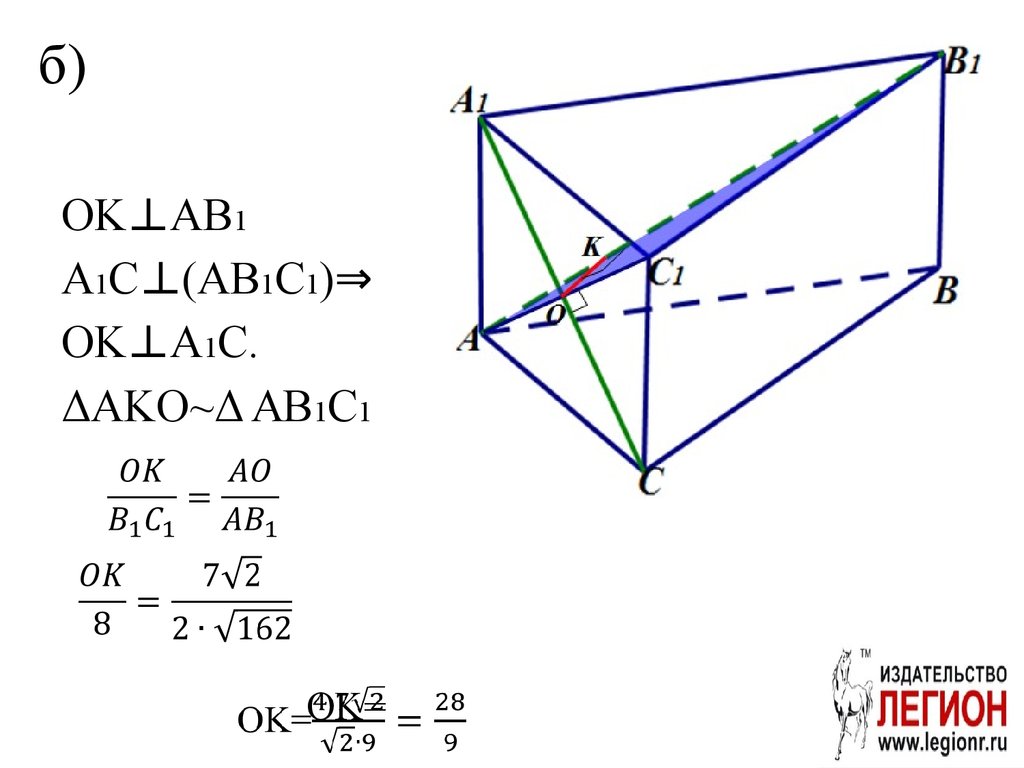
б)OK⊥AB1
A1C⊥(AB1C1)⇒
OK⊥A1C.
ΔAKO~Δ AB1C1
OK=
16.
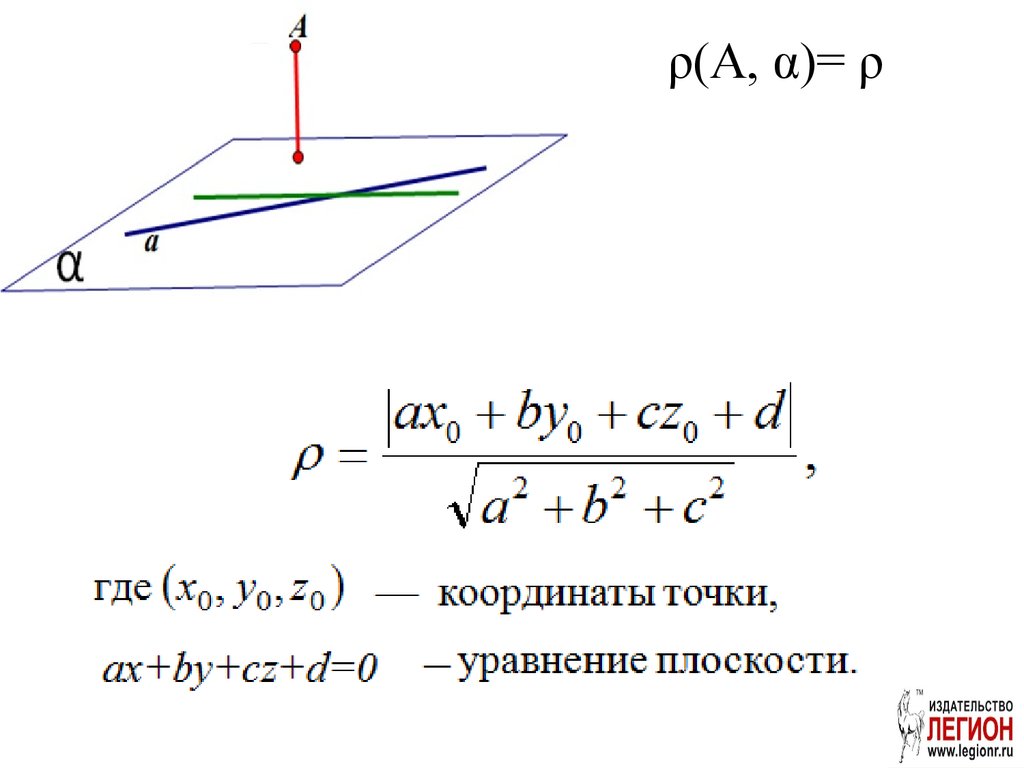
ρ(a,b)=ρ(A, α)17.
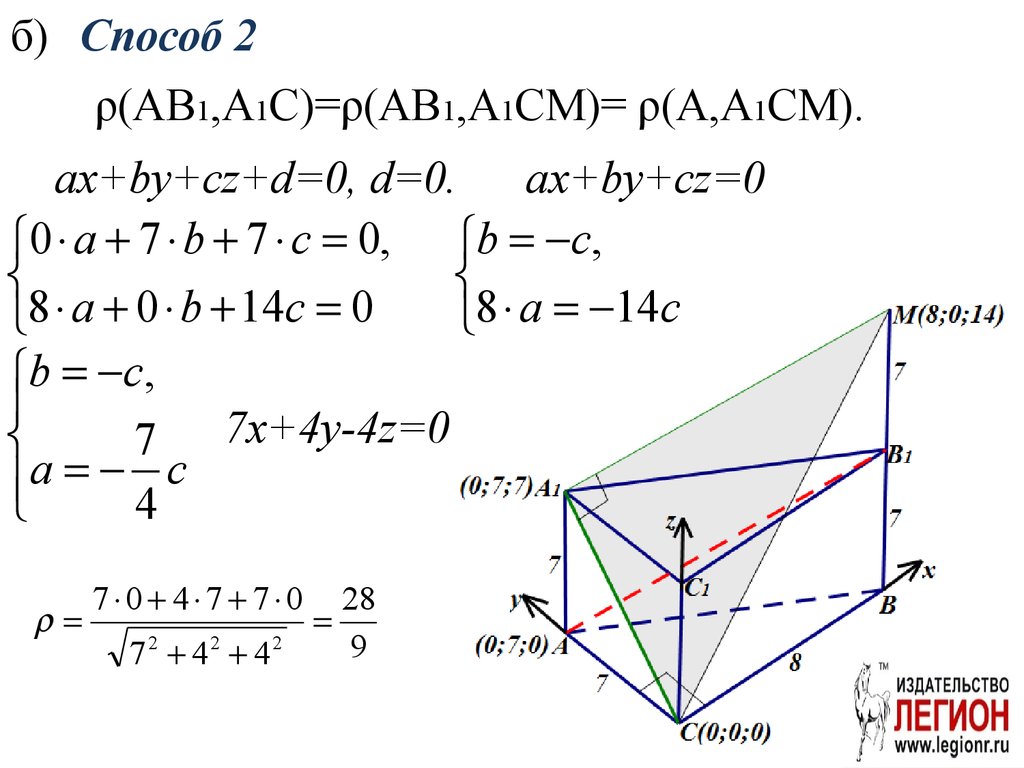
б) Способ 2ρ(AB1,A1C)=ρ(AB1,A1CM)= ρ(A,A1CM).
ax+by+cz+d=0, d=0.
ax+by+cz=0
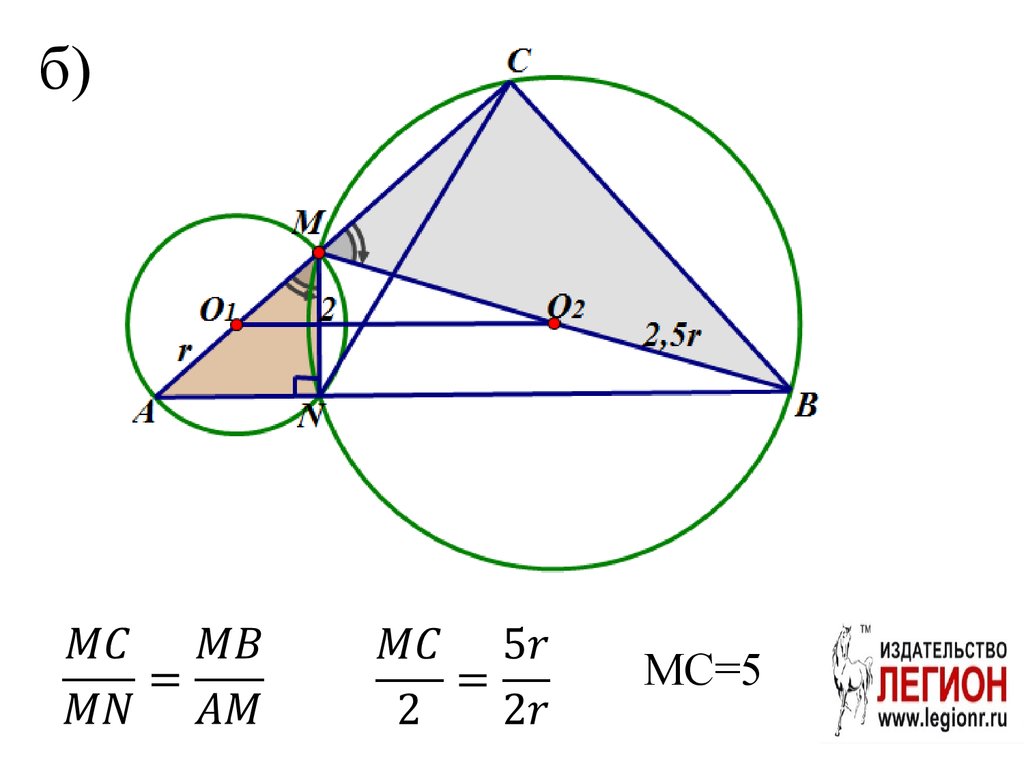
0 a 7 b 7 c 0, b c,
8 a 0 b 14c 0
8 a 14c
b c,
7 7x+4y-4z=0
a c
4
7 0 4 7 7 0
7 2 42 42
28
9
18. Основные методы построения сечений многогранников
АксиоматическийМетод следов
Метод вспомогательных сечений
(метод внутреннего проектирования)
Комбинированный метод
19. Метод следов
Понятие следа• Линия пересечения плоскости сечения и плоскости
грани многогранника называется следом секущей
плоскости на плоскости этой грани
многогранника.
• Точка пересечения плоскости сечения и прямой,
содержащей ребро многогранника, называется
следом секущей плоскости на прямой,
содержащей это ребро многогранника.
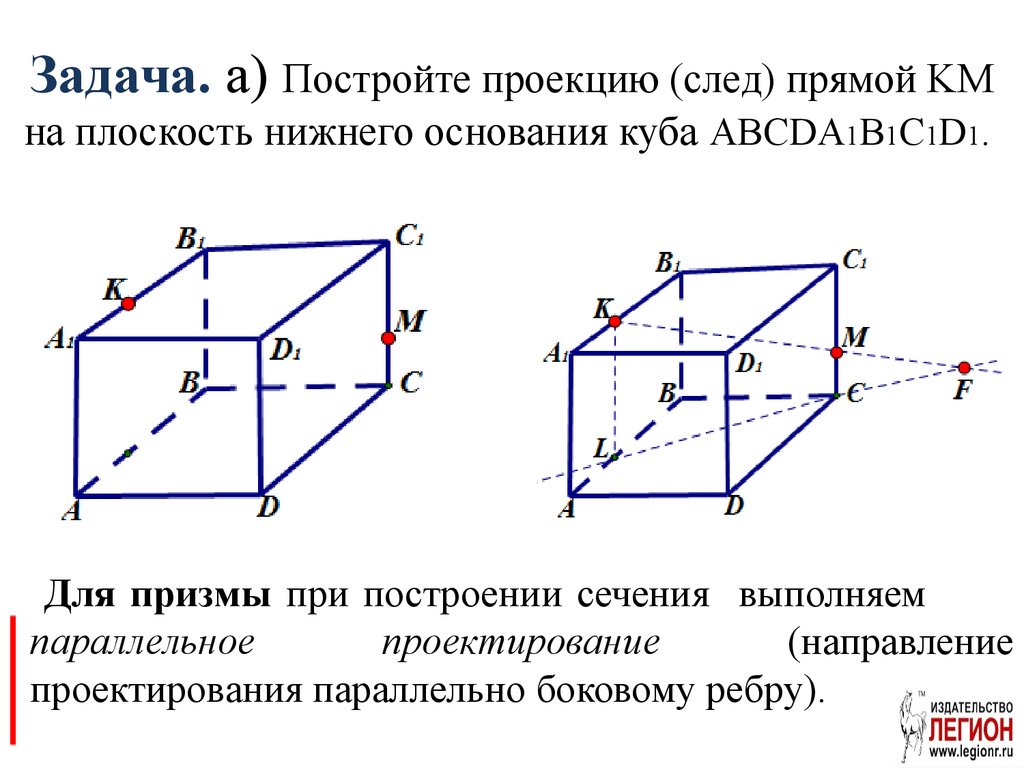
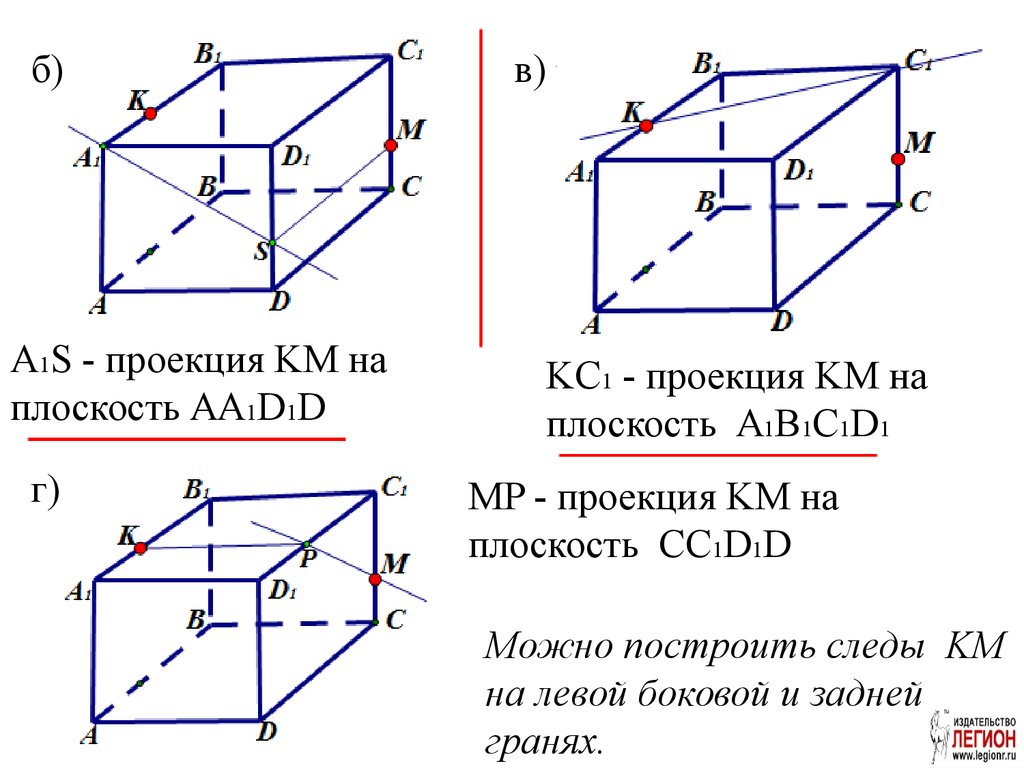
20. Задача. а) Постройте проекцию (след) прямой KM на плоскость нижнего основания куба ABCDA1B1C1D1.
Для призмы при построении сечения выполняемпараллельное
проектирование
(направление
проектирования параллельно боковому ребру).
21.
б)A1S - проекция KM на
плоскость AA1D1D
г)
в)
KC1 - проекция KM на
плоскость A1B1C1D1
MP - проекция KM на
плоскость CC1D1D
Можно построить следы KM
на левой боковой и задней
гранях.
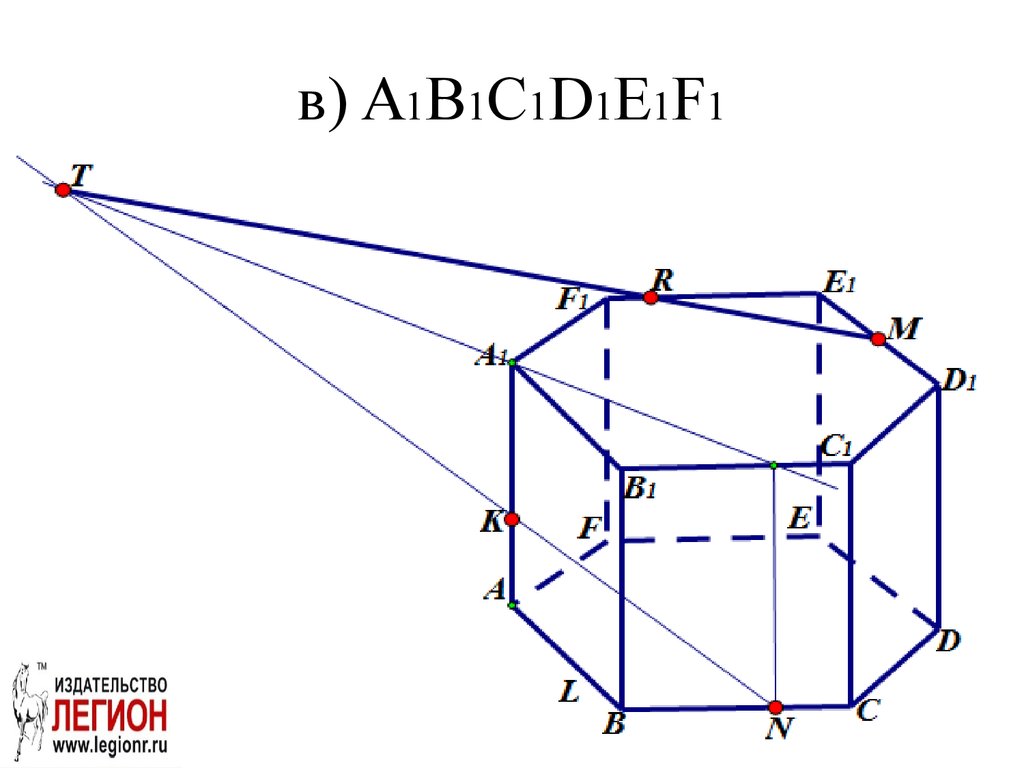
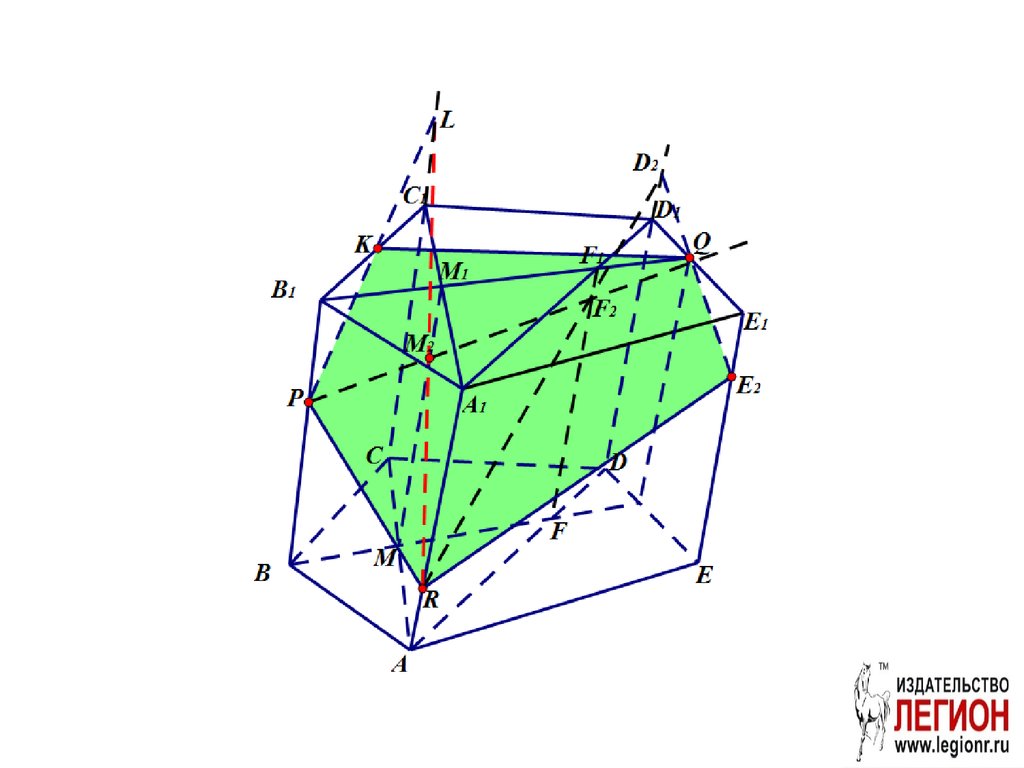
22. Задача. ABCDEFA1B1С1D1E1F1 правильная шестиугольная призма. Постройте проекцию (след) плоскости сечения MNK на плоскости: а)
Задача. ABCDEFA B С D E F правильная шестиугольная призма. Постройте проекцию (след) плоскости сечения MNK на плоскости:1
а) ABC; б) AA1B1B;
в) A1B1С1D1E1F1;
г) DD1E1E;
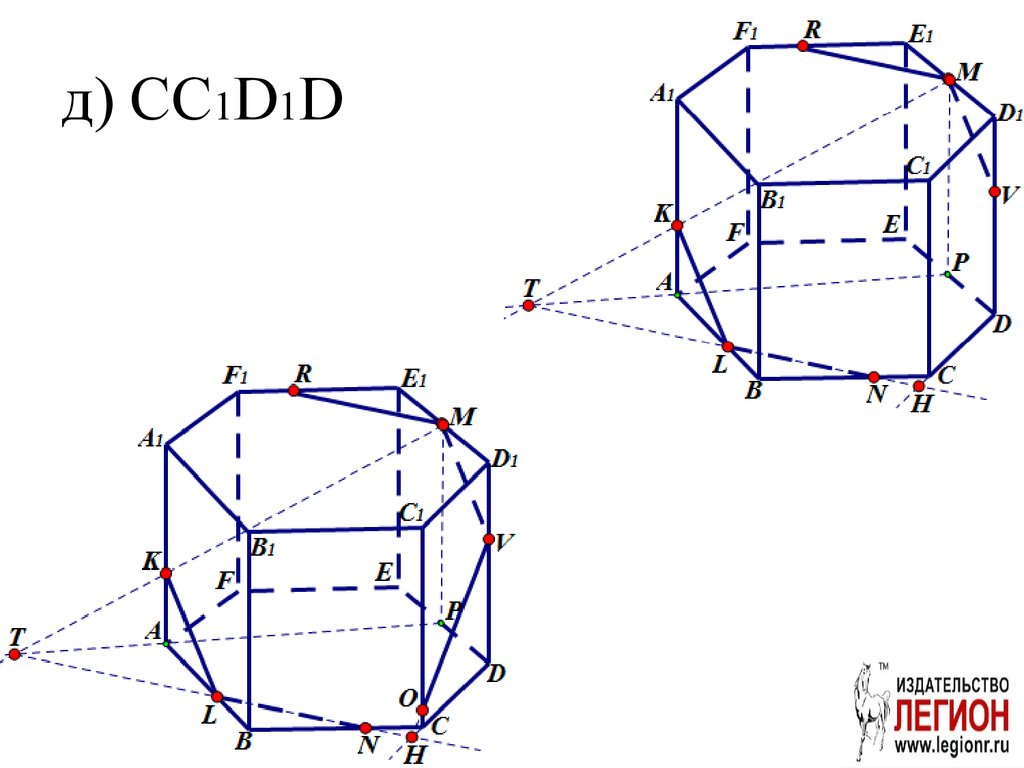
д) CC1D1D.
1
1
1
1
1
23.
а)24.
б) AA1B1B25. в) A1B1С1D1E1F1
26. Комбинированный метод
Сочетание применения теорем опараллельности прямых и плоскостей в
пространстве и аксиоматического метода.
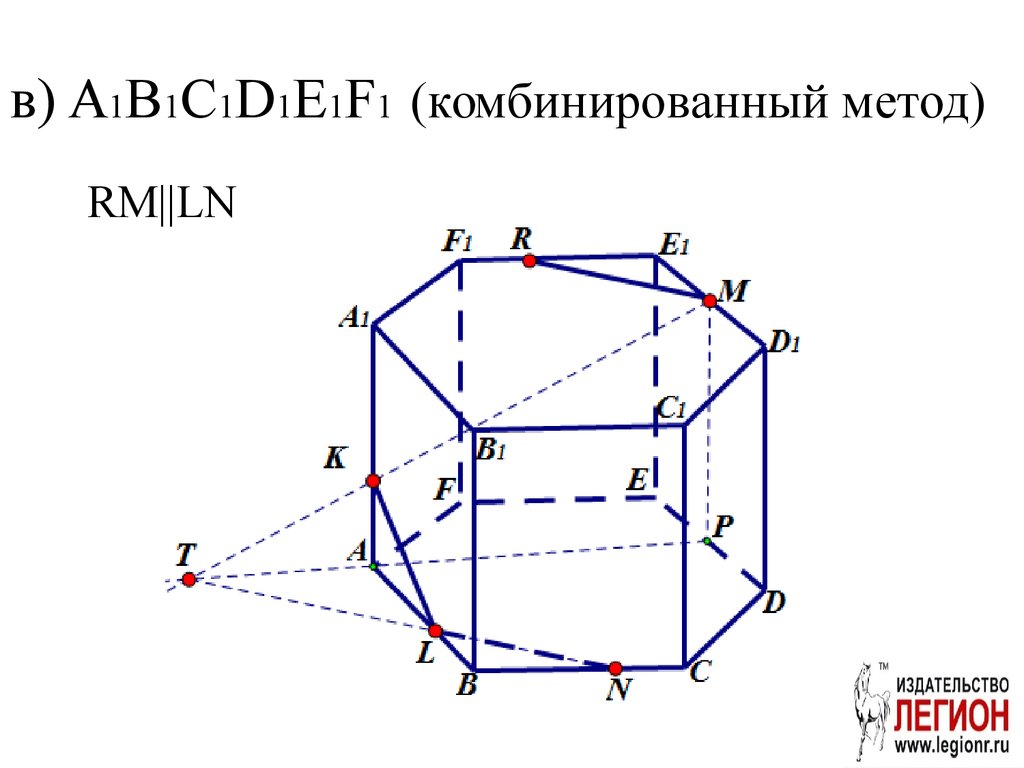
27. в) A1B1С1D1E1F1 (комбинированный метод)
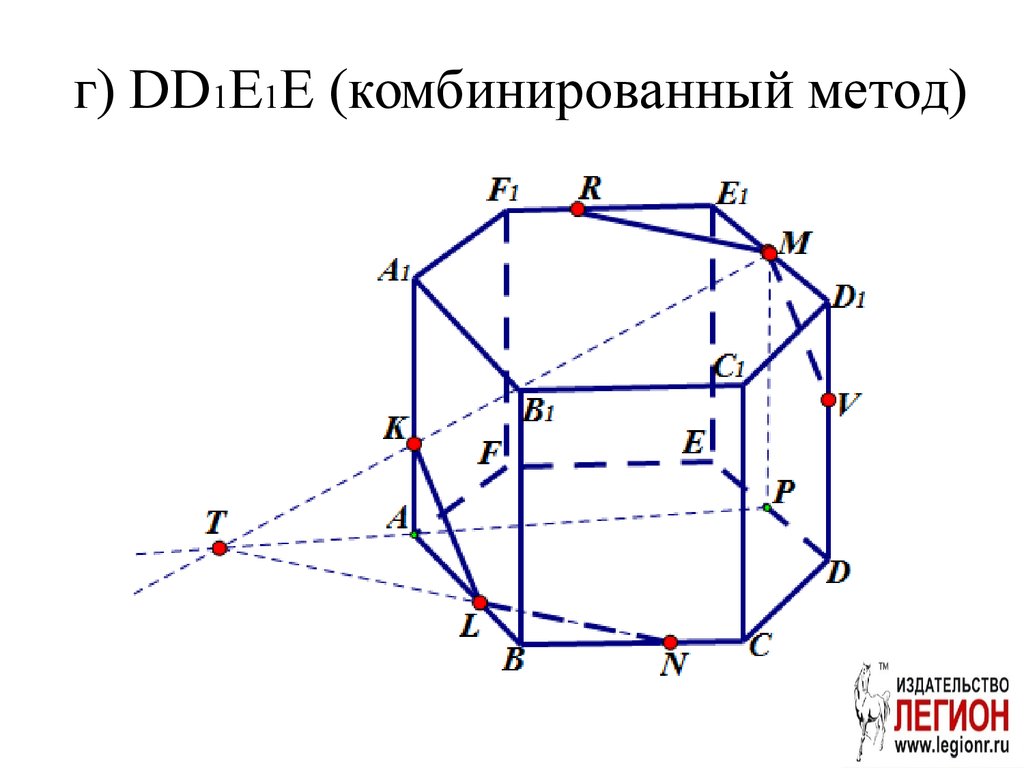
RM||LN28. г) DD1E1E (комбинированный метод)
29. д) CC1D1D
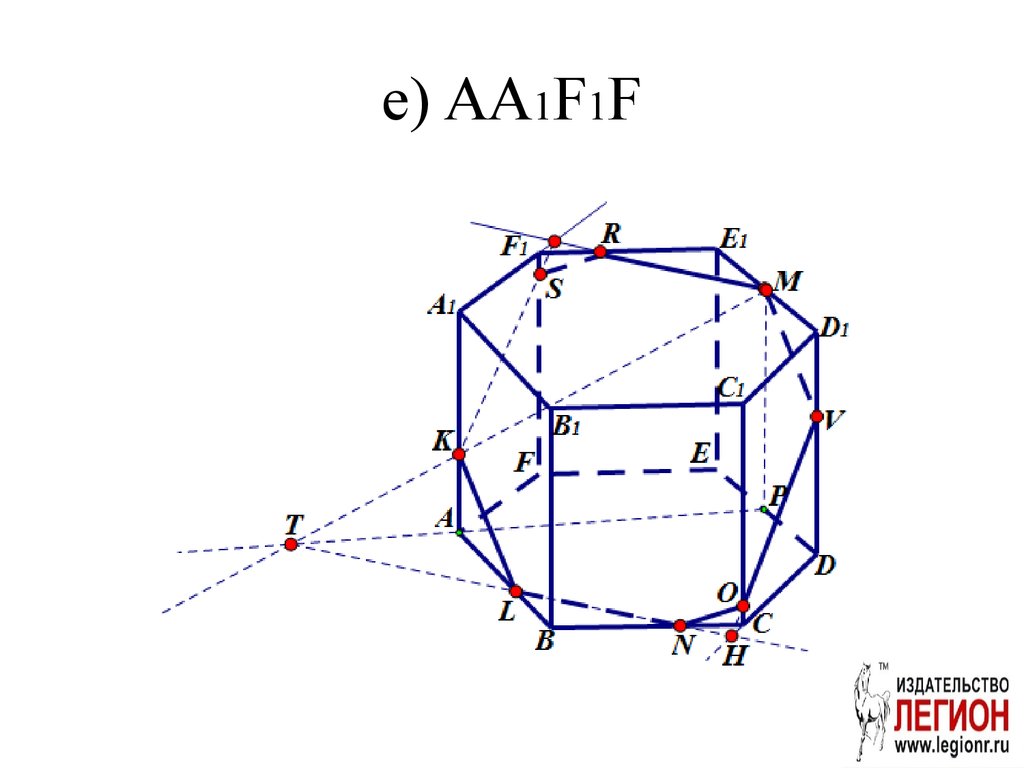
30. e) AA1F1F
31.
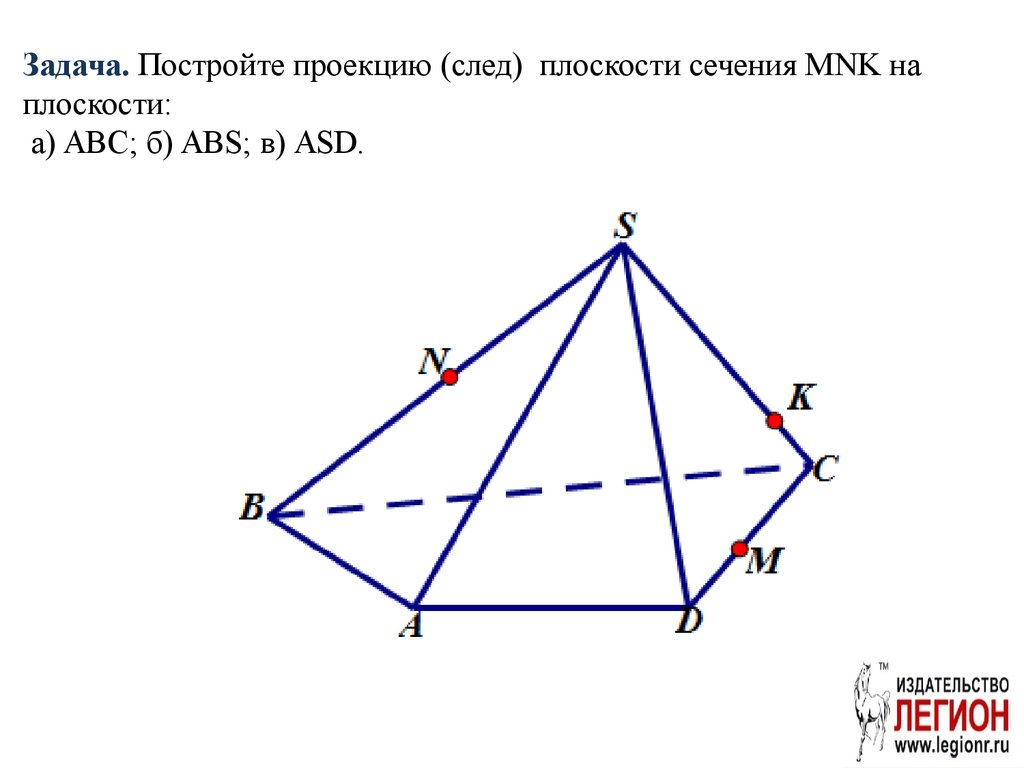
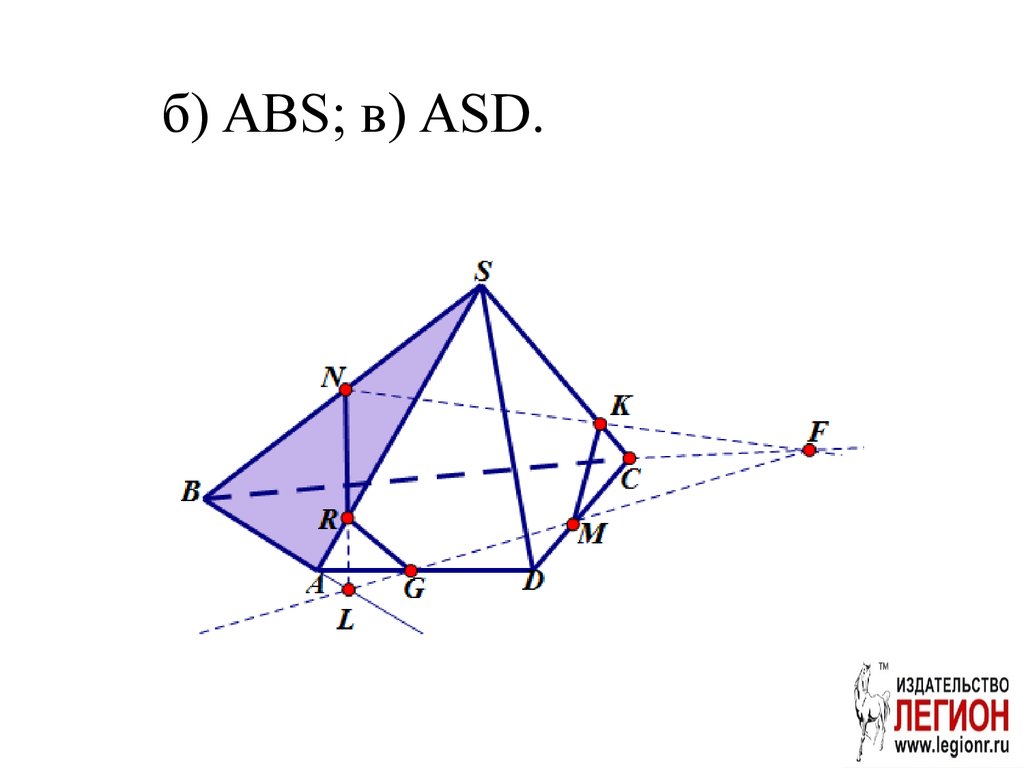
32. Задача. Постройте проекцию (след) плоскости сечения MNK на плоскости: а) ABC; б) ABS; в) ASD.
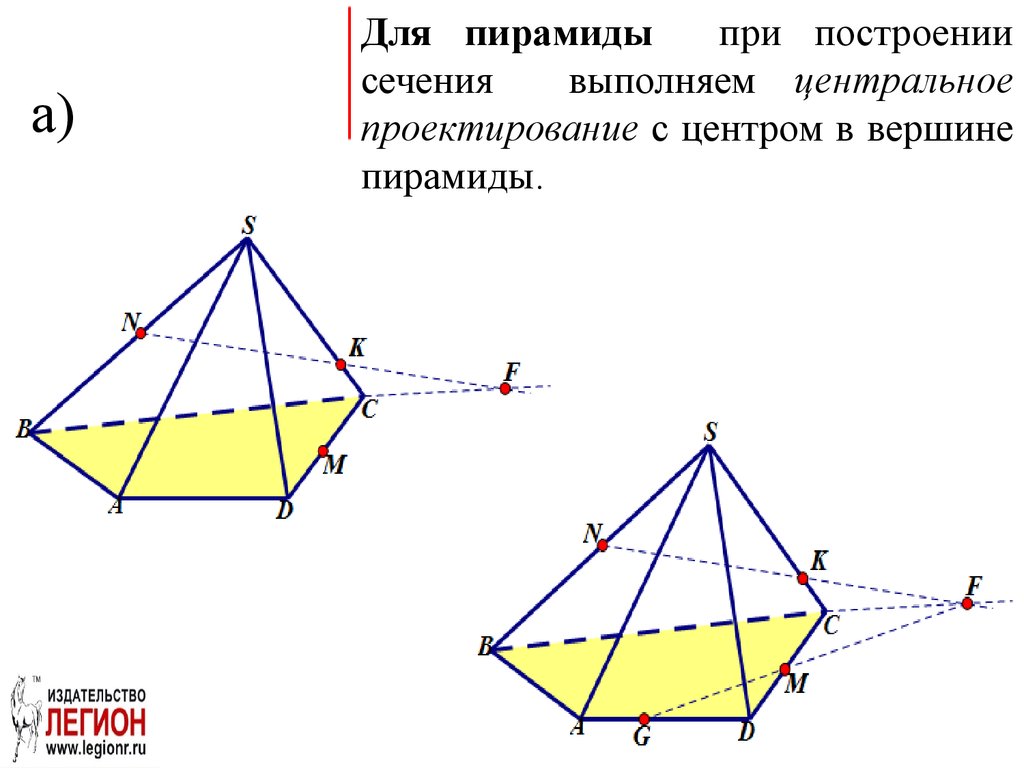
33.
а)Для пирамиды
при построении
сечения
выполняем центральное
проектирование с центром в вершине
пирамиды.
34.
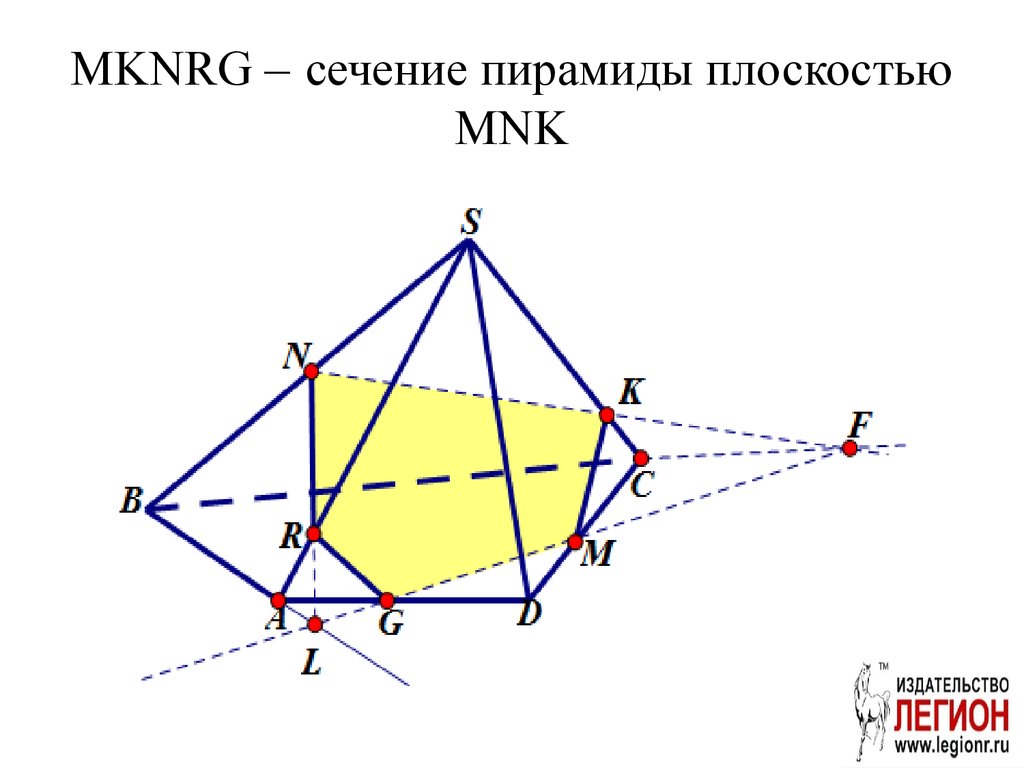
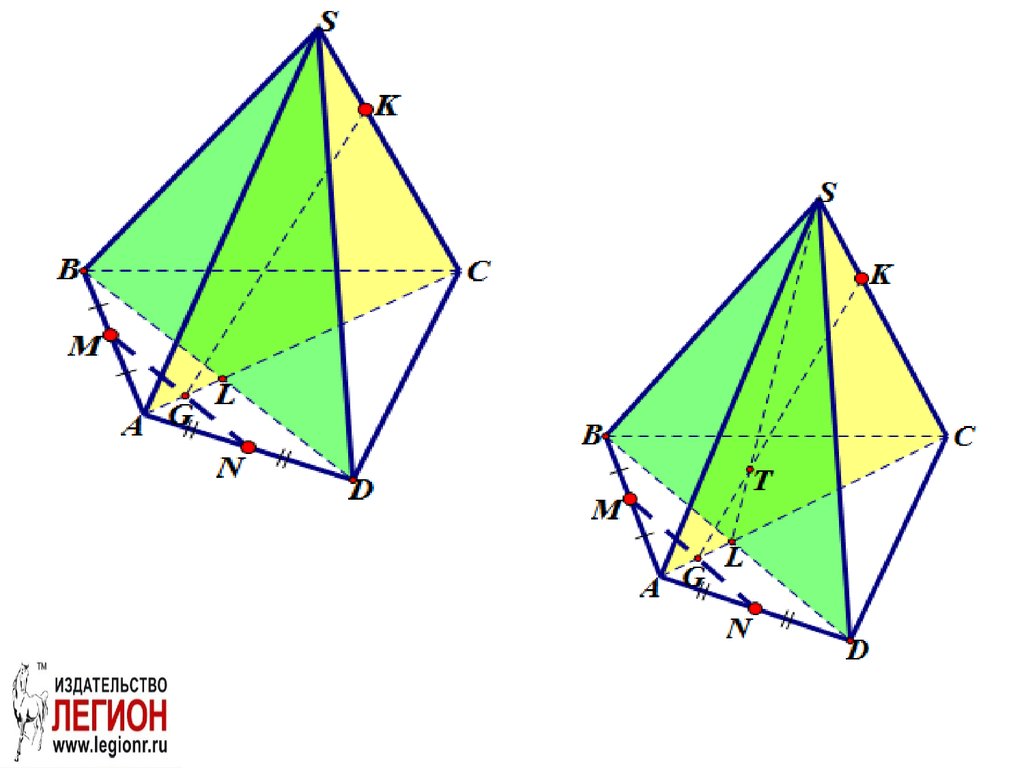
б) ABS; в) ASD.35. MKNRG – сечение пирамиды плоскостью MNK
36. Метод вспомогательных сечений (метод внутреннего проектирования)
Универсальный метод, основанный напостроении вспомогательных плоскостей,
не выходящих за пределы многогранника.
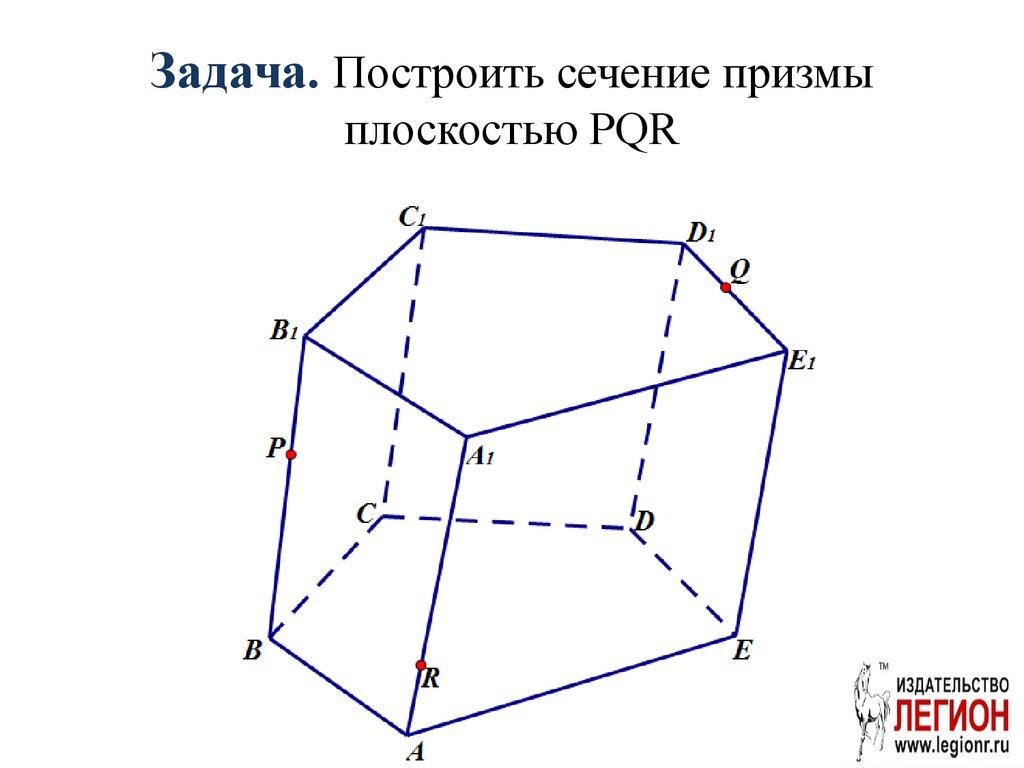
37. Задача. Построить сечение призмы плоскостью PQR
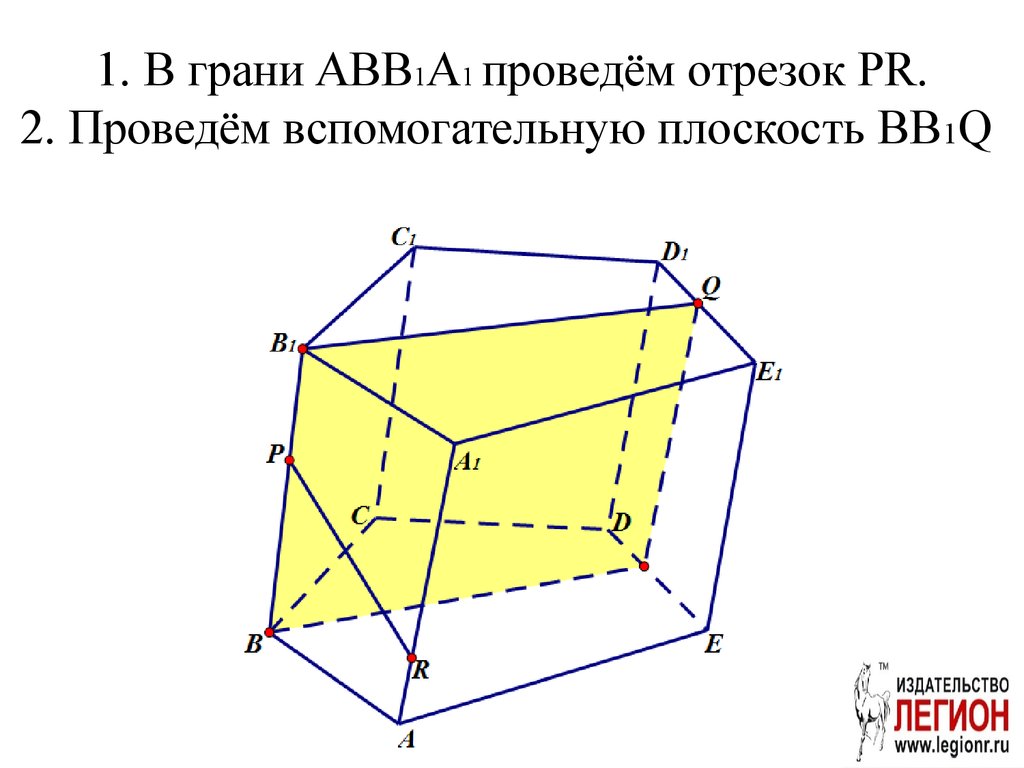
38. 1. В грани ABB1A1 проведём отрезок PR. 2. Проведём вспомогательную плоскость BB1Q
39.
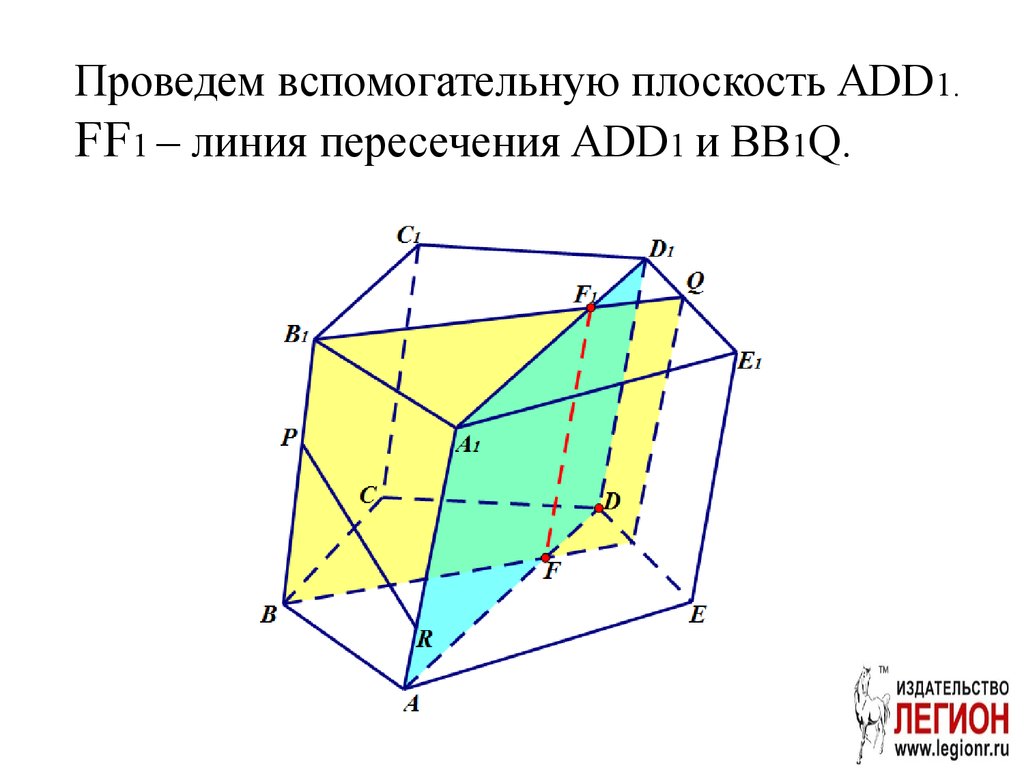
Проведем вспомогательную плоскость ADD1.FF1 – линия пересечения ADD1 и BB1Q.
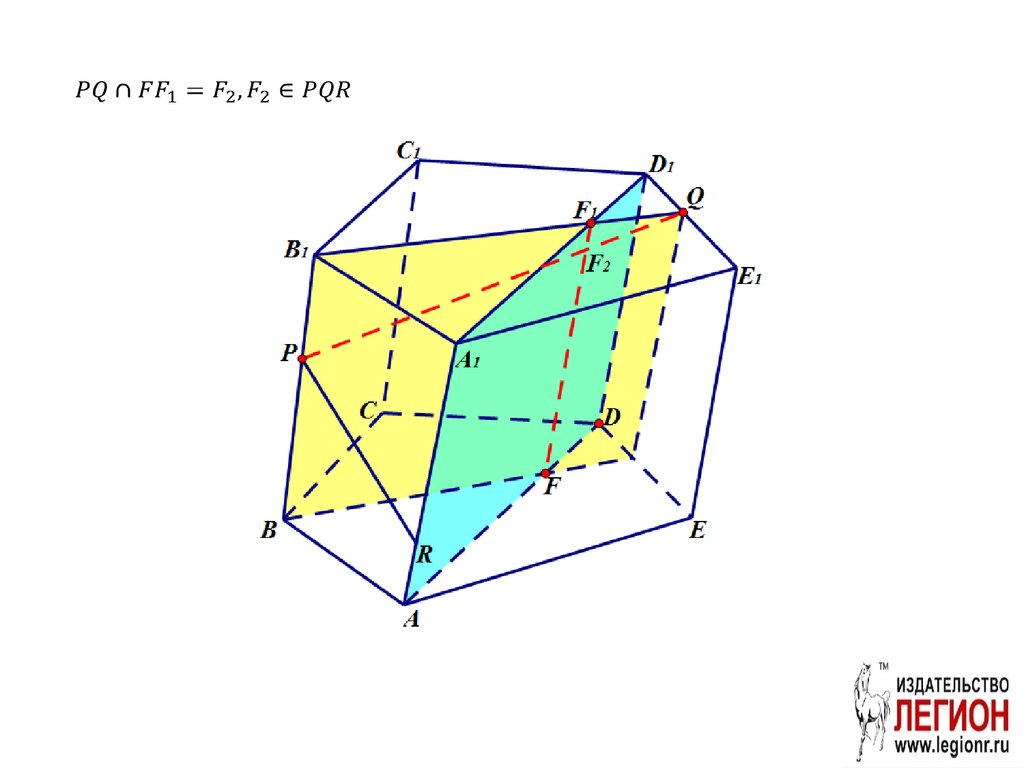
40.
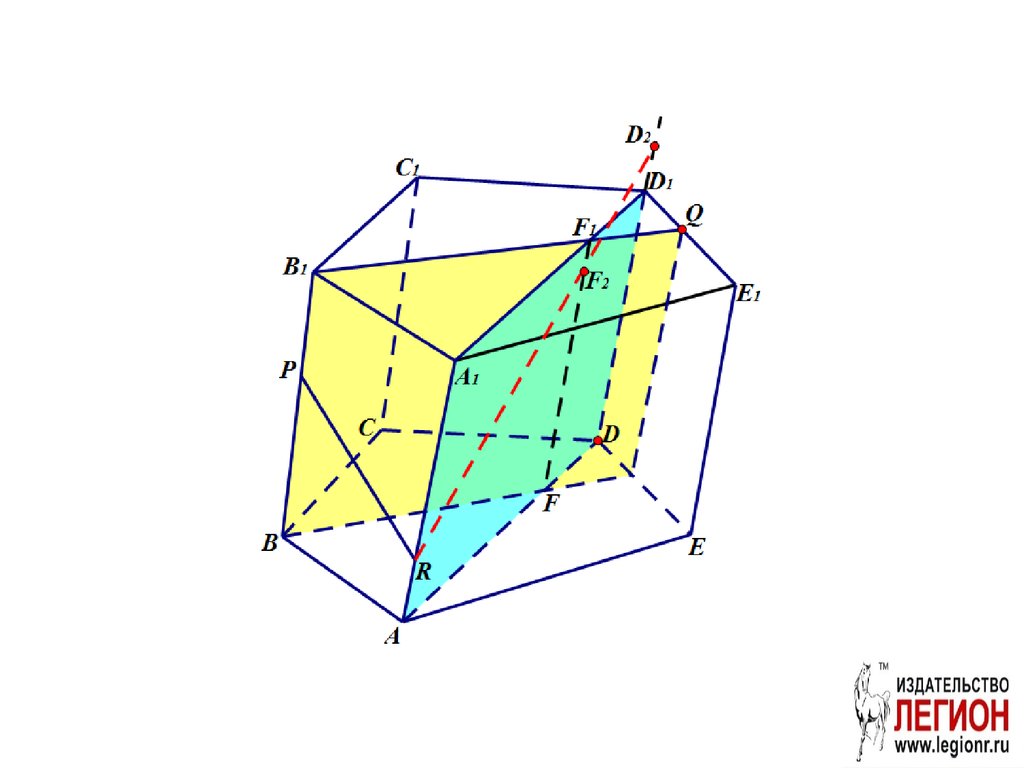
41.
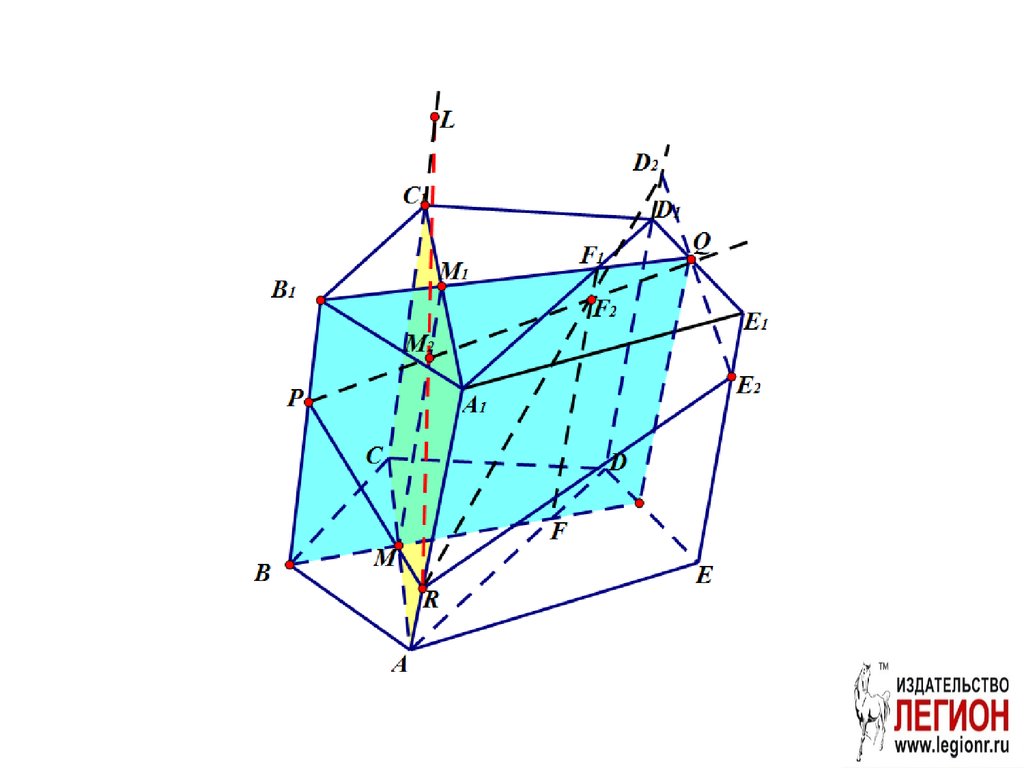
42.
43.
44.
45.
46.
47.
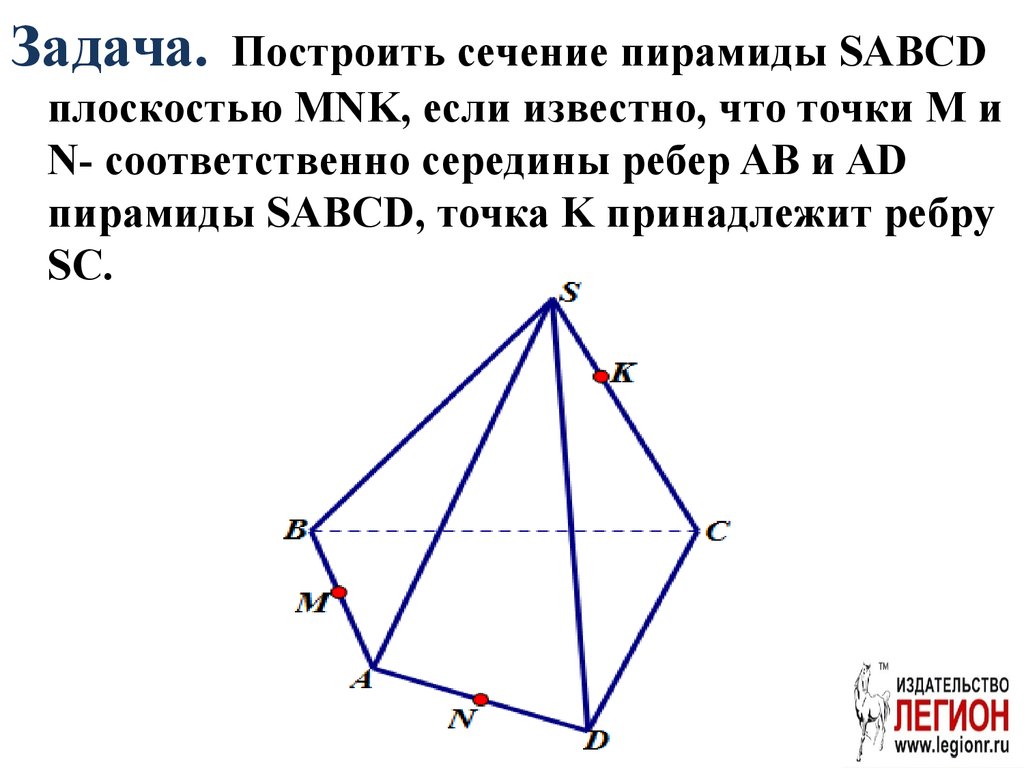
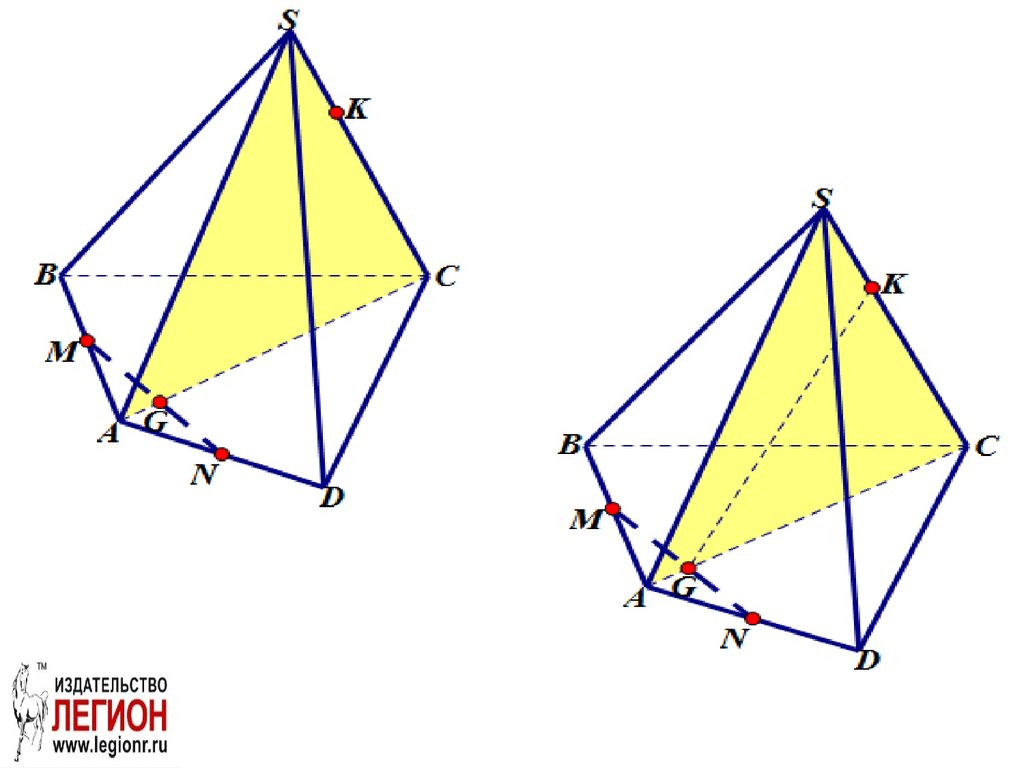
Задача.Построить сечение пирамиды SABCD
плоскостью MNK, если известно, что точки M и
N- соответственно середины ребер AB и AD
пирамиды SABCD, точка K принадлежит ребру
SC.
48.
49.
50.
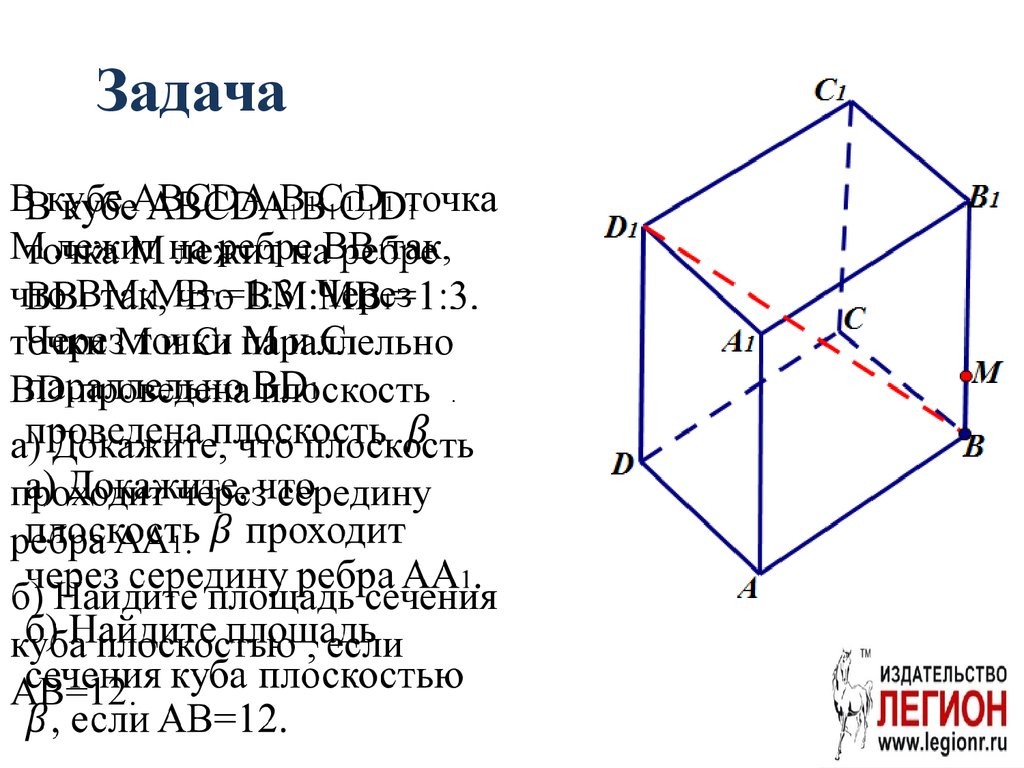
51. Задача
В кубе ABCDA 1B1C1D1 точкаM лежит на ребре BB1так,
что BM:MB1=1:3. Через
точки M и С1 параллельно
BD1проведена плоскость .
а) Докажите, что плоскость
проходит через середину
ребра AA1.
б) Найдите площадь сечения
куба плоскостью , если
AB=12.
52.
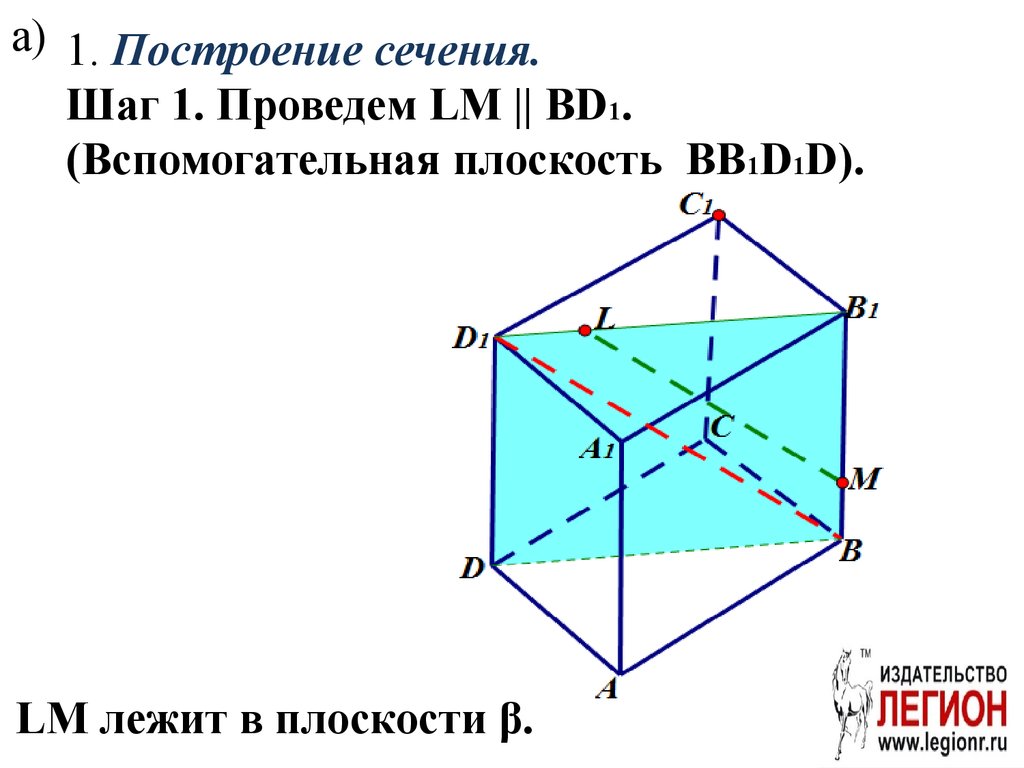
а) 1. Построение сечения.Шаг 1. Проведем LM || BD1.
(Вспомогательная плоскость BB1D1D).
LM лежит в плоскости β.
53.
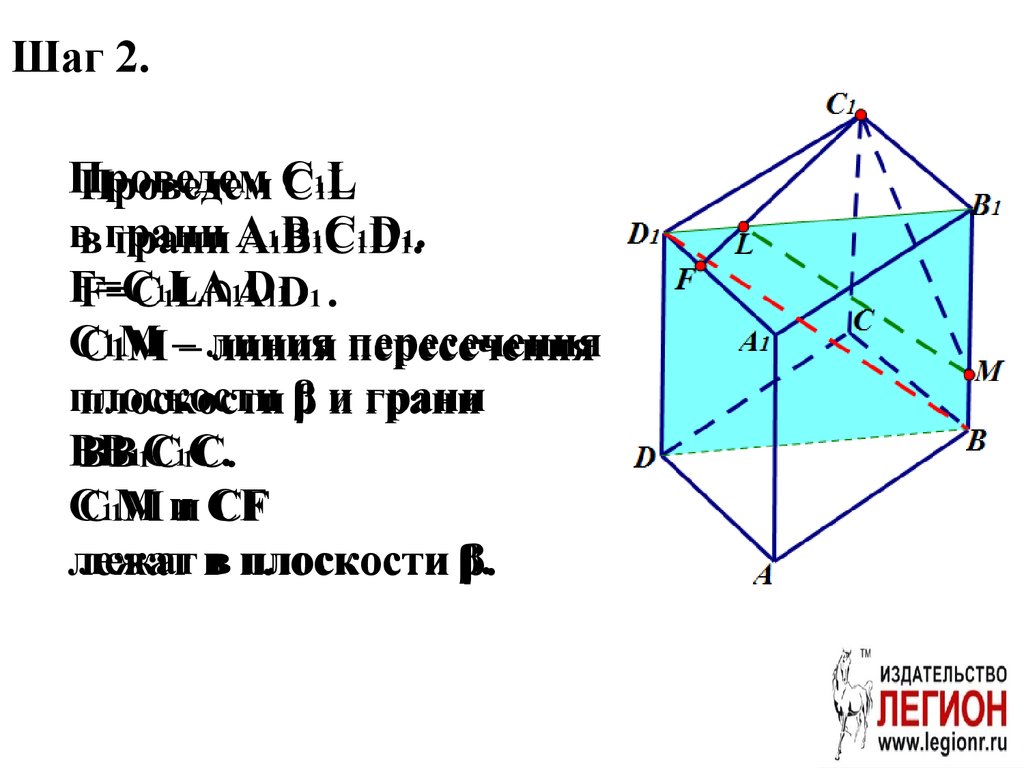
Шаг 2.Проведем С1L
в грани A1B1C1D1.
F=С1LA1D1 .
С1М – линия пересечения
плоскости β и грани
BB1C1C.
C1M и CF
лежат в плоскости β.
54.
Шаг 3.Проведем FK||C1M.
FK-линия пересечения
грани AA1D1D
и плоскости β.
KM – линия пересечения
грани AA1B1B
и плоскости β.
55.
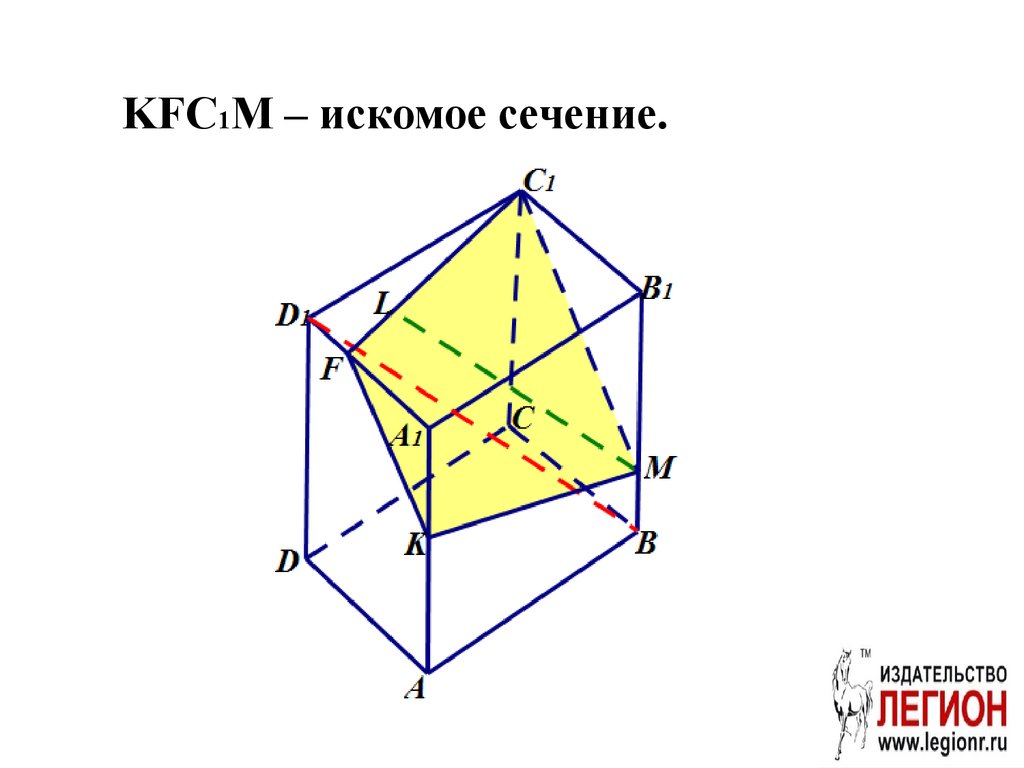
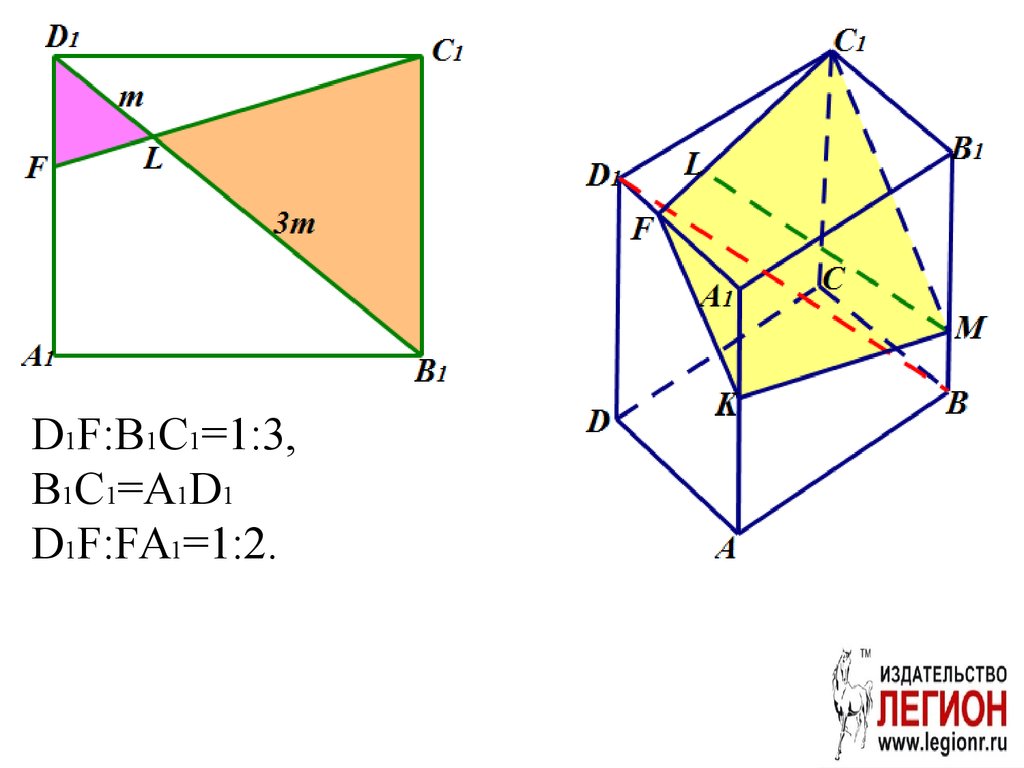
KFC1M – искомое сечение.56. 2. Доказательство
B1L:LD1=3:1 (по теореме Фалеса)57.
D1F:B1C1=1:3,B1C1=A1D1
D1F:FA1=1:2.
58.
Проведем D1E||C1M.A1F:FD1=A1K:KE=2:1.
A1E:EA=3:1.
Следовательно, A1K=KA.
β проходит через
середину ребра AA1.
б)
59.
Сечение KFC1M – трапеция, AB=12 по условию.· FH
: KF=
KF=10.
:=
: F=
KM
60.
KP=FH10x=18, x=1,8,
KP=
· FH=· =
=30.
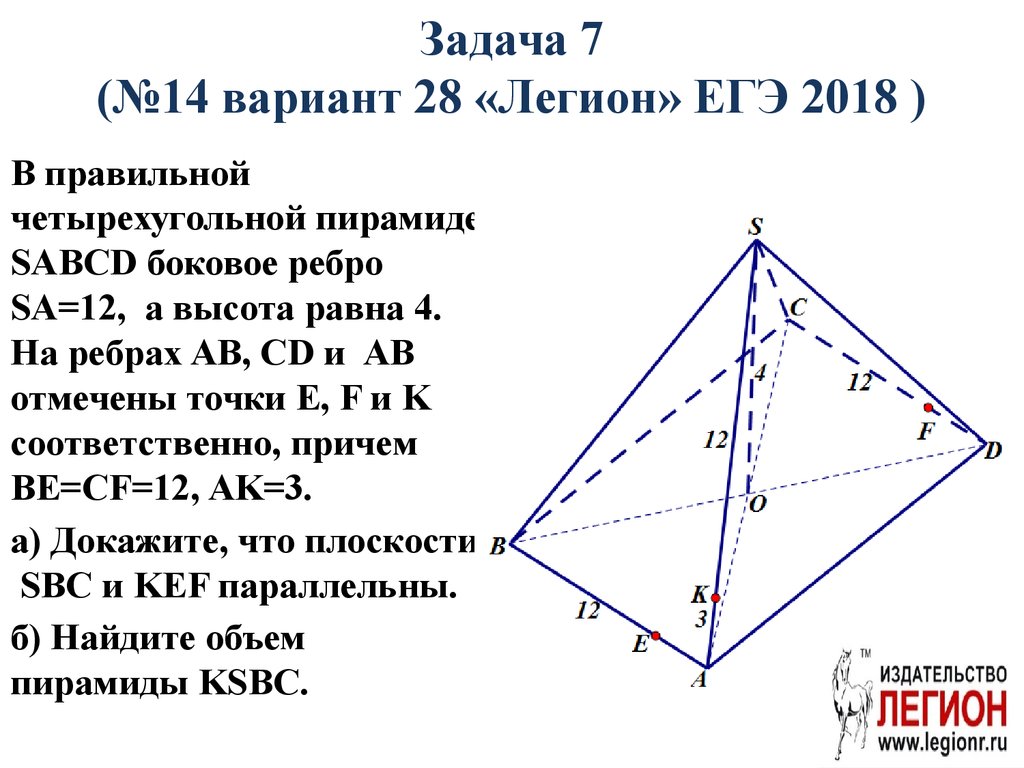
61. Задача 7 (№14 вариант 28 «Легион» ЕГЭ 2018 )
В правильнойчетырехугольной пирамиде
SABCD боковое ребро
SA=12, а высота равна 4.
На ребрах AB, CD и AB
отмечены точки E, F и K
соответственно, причем
BE=CF=12, AK=3.
а) Докажите, что плоскости
SBC и KEF параллельны.
б) Найдите объем
пирамиды KSBC.
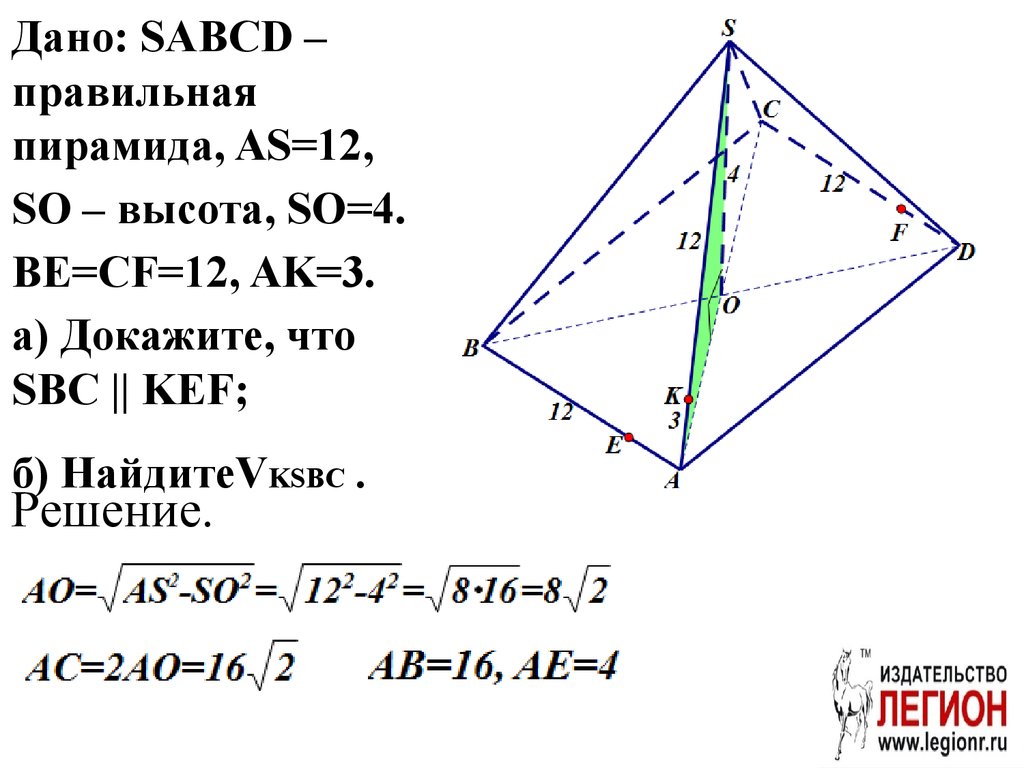
62.
Дано: SABCD –правильная
пирамида, AS=12,
SO – высота, SO=4.
BE=CF=12, AK=3.
а) Докажите, что
SBC || KEF;
б) НайдитеVKSBC .
Решение.
63.
64. Решение.
Способ 1• ||KEF ⇔
SBC
={l; m; n}
={; ; -1}
={; ; -1}
(векторы нормалей).
65. Способ 2
•SBC||KEF⇔(SB||EK и BC||EF)
ΔSBA~ΔAEK: , ∠SAB – общий,
⇒ SB||EK .
AE=FD=4, ⇒EF||BC.
66.
•б) VKSBC==SC·sin∠SBC (cos ∠SBC =)
или= SH,
где SH – высота ΔSBC.
=
Уравнение плоскости SBC:
x+y-z+d=0, где ={; ; -1} - вектор нормали к
плоскости SBC.
d: S(0;0;4)
67.
ρ(A, α)= ρ68.
•BSC:x+ y – z + 4=0
K(6; 0;1)
=
VKSBC==·· =128
69.
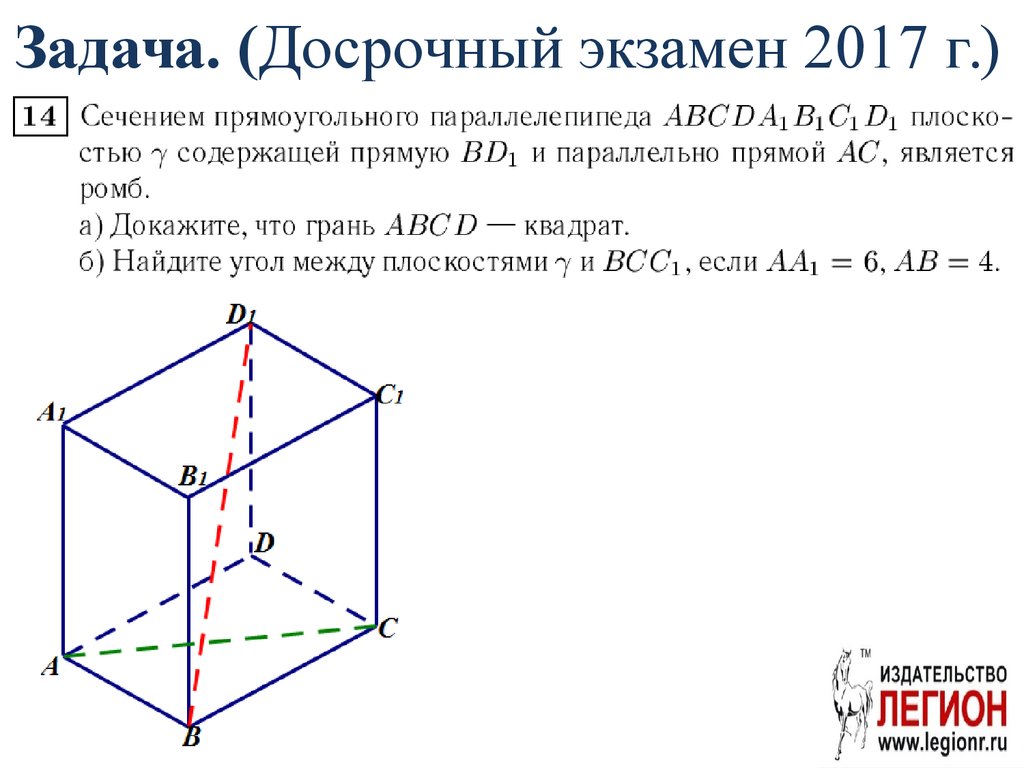
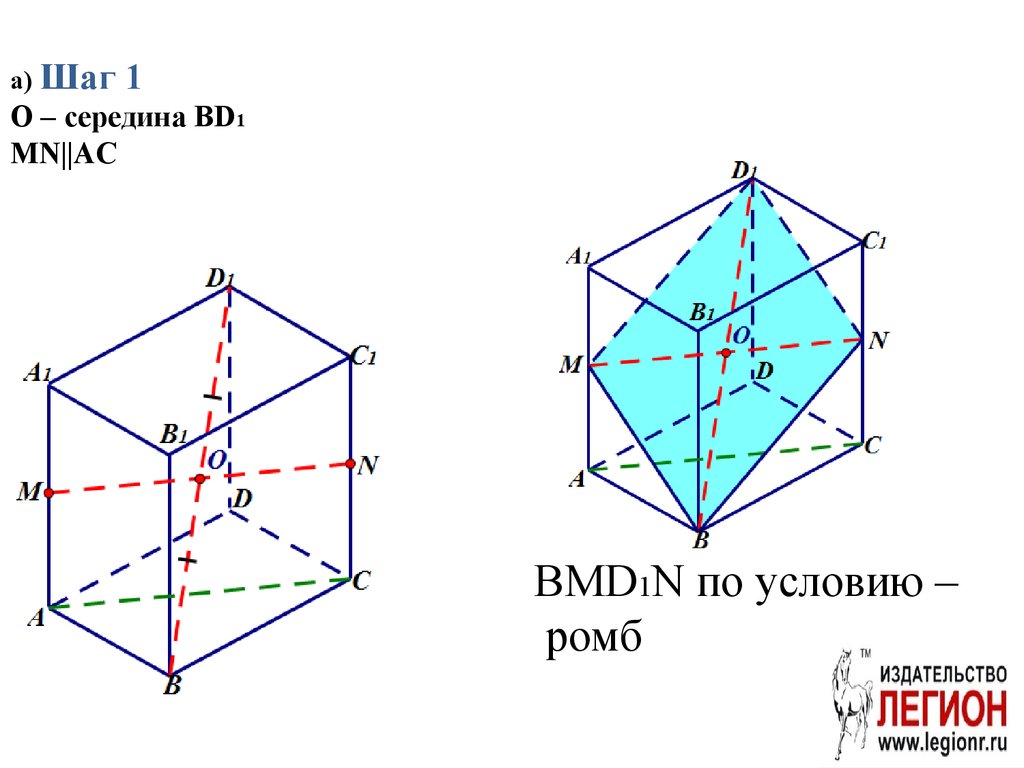
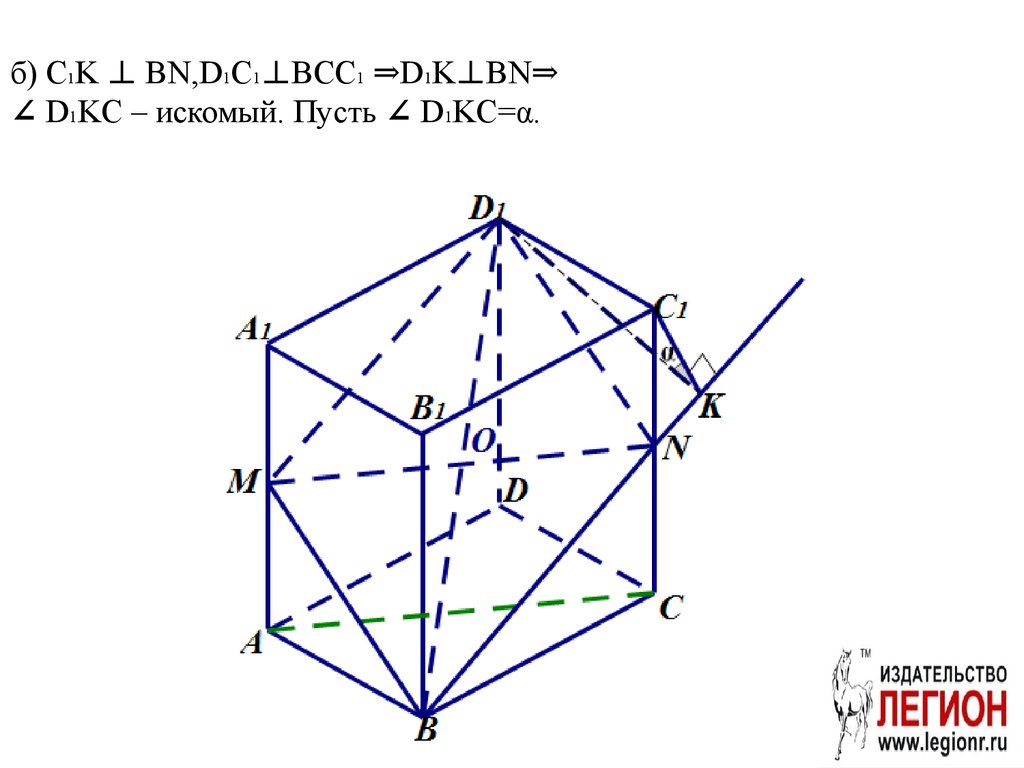
Задача. (Досрочный экзамен 2017 г.)70. а) Шаг 1 O – середина BD1 MN||AC
BMD1N по условию –ромб
71. Шаг 2
∆ABM=∆BNCпо катету и гипотенузе,
откуда AB=BC,
значит прямоугольник
ABCD – квадрат.
72. б) C1K ⊥ BN,D1C1⊥BCC1 ⇒D1K⊥BN⇒ ∠ D1KC – искомый. Пусть ∠ D1KC=α.
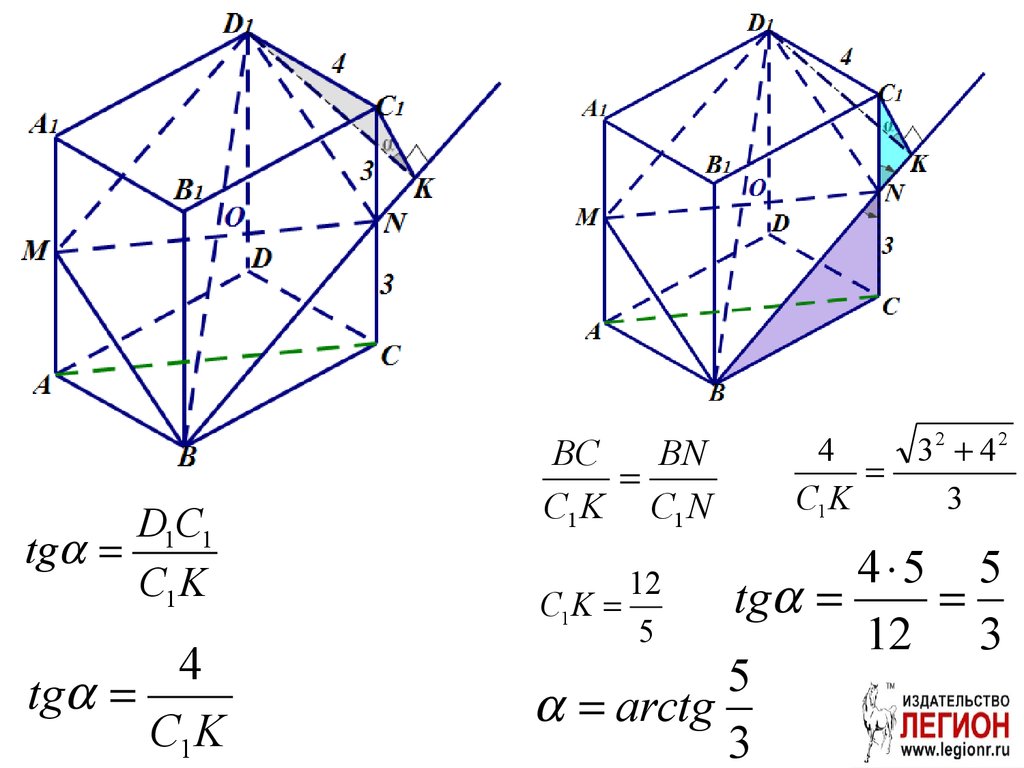
73.
D1C1tg
С1 K
4
tg
С1 K
BC
BN
С1 K С1 N
4
32 4 2
С1 K
3
4 5 5
tg
12 3
5
arctg
3
12
C1 K
5
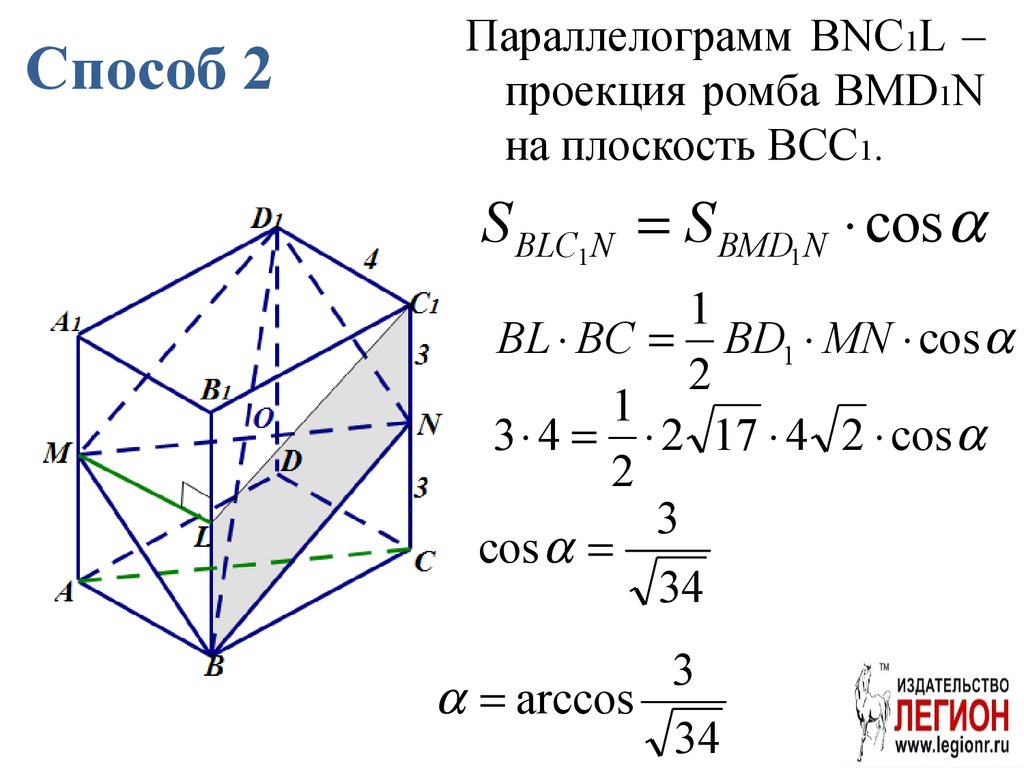
74. Способ 2
Параллелограмм BNC1L –проекция ромба BMD1N
на плоскость BCC1.
S BLC1 N S BMD1 N cos
1
BL BC BD1 MN cos
2
1
3 4 2 17 4 2 cos
2
3
cos
34
3
arccos
34
75.
Способ 376.
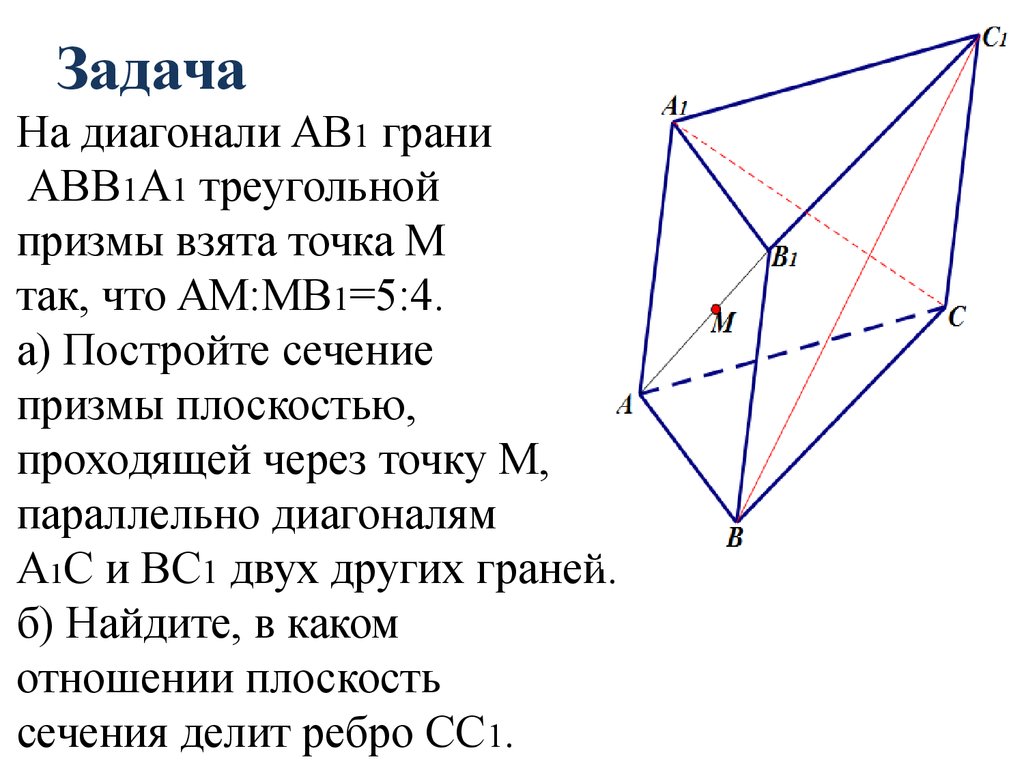
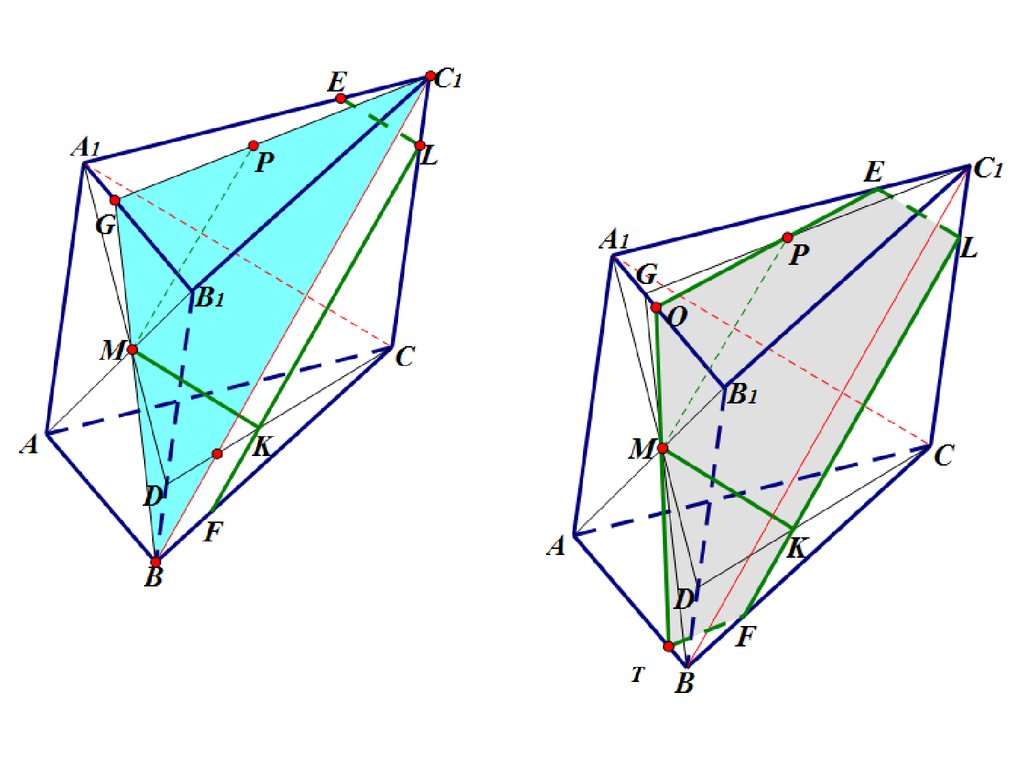
77. Задача
На диагонали AB1 граниABB1А1 треугольной
призмы взята точка M
так, что AM:MB1=5:4.
а) Постройте сечение
призмы плоскостью,
проходящей через точку M,
параллельно диагоналям
A1С и BC1 двух других граней.
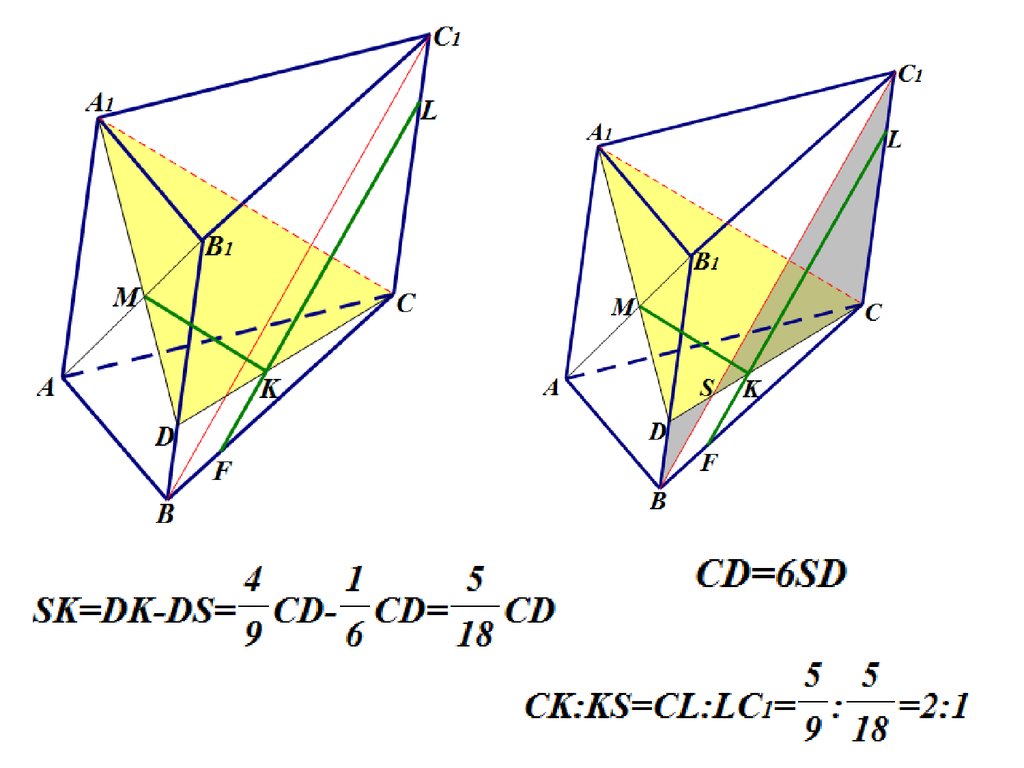
б) Найдите, в каком
отношении плоскость
сечения делит ребро СС1.
78.
79.
80.
81. Демонстрационный вариант ЕГЭ 2018 задание 16
82.
83.
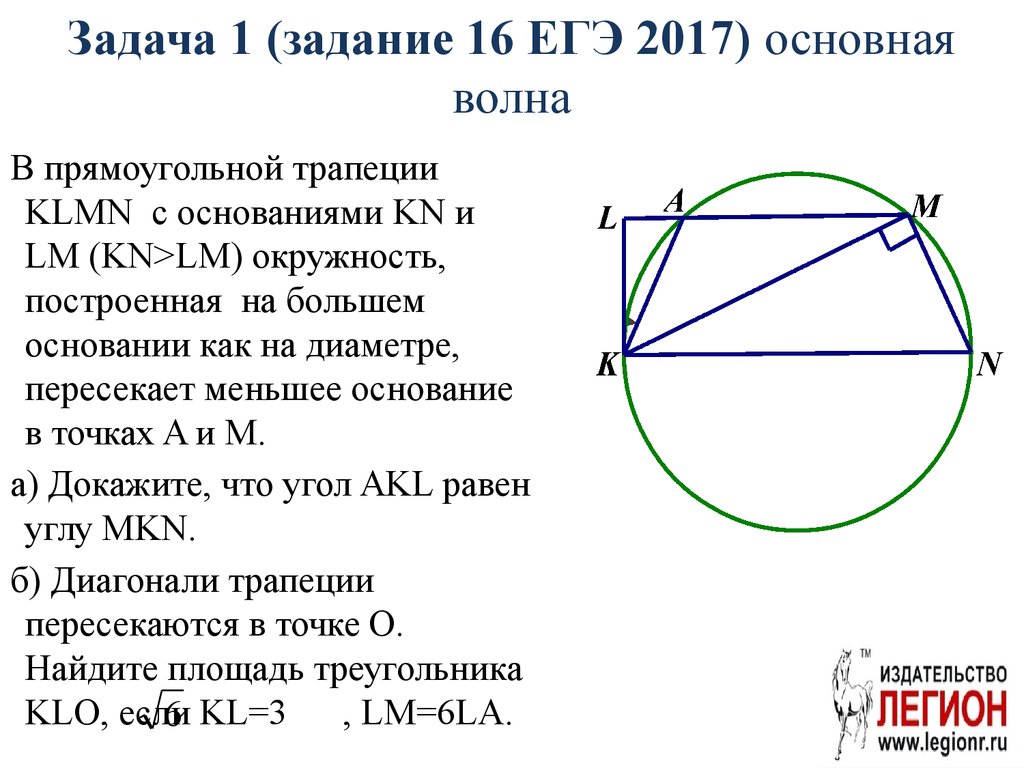
84. Задача 1 (задание 16 ЕГЭ 2017) основная волна
В прямоугольной трапецииKLMN с основаниями KN и
LM (KN>LM) окружность,
построенная на большем
основании как на диаметре,
пересекает меньшее основание
в точках A и M.
а) Докажите, что угол AKL равен
углу MKN.
б) Диагонали трапеции
пересекаются в точке O.
Найдите площадь треугольника
KLO, если
6 KL=3 , LM=6LA.
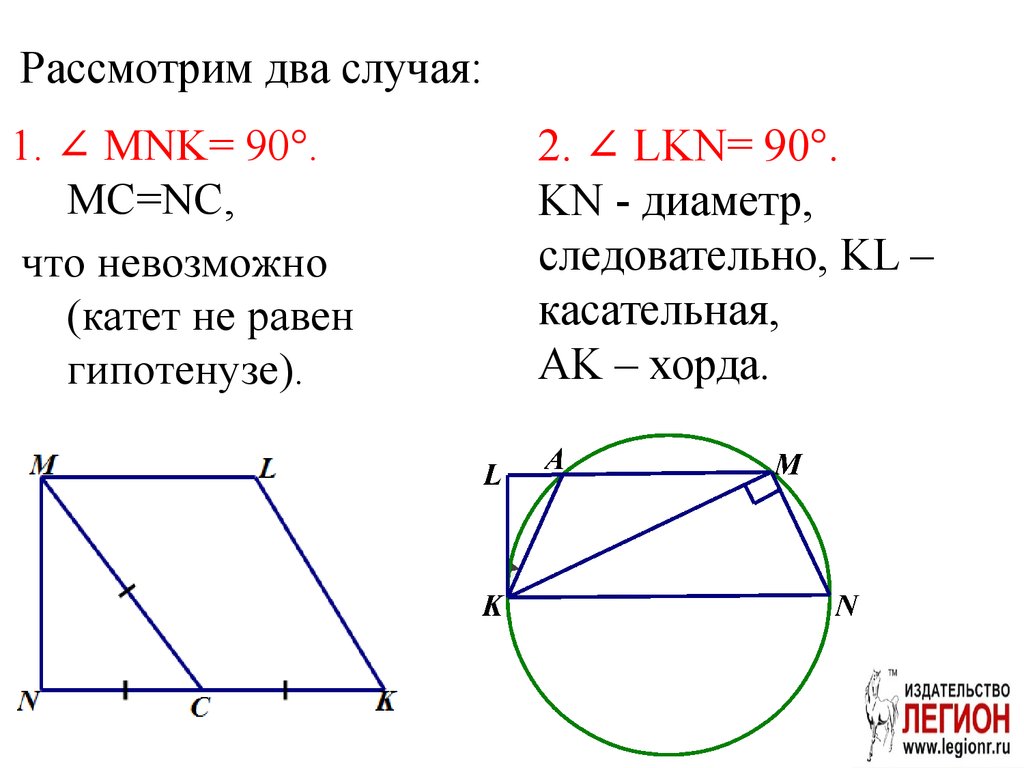
85. Рассмотрим два случая:
1. ∠ MNK= 90°.MC=NC,
что невозможно
(катет не равен
гипотенузе).
2. ∠ LKN= 90°.
KN - диаметр,
следовательно, KL –
касательная,
AK – хорда.
86. Решение.
1а) ∠AKL= AK
2
AK MN
,∠
1
=MN
MKN
2
∠AKL= ∠ MKN.
б)
3 6
6AL2=6·9, AL=3, LM=18,
∆AKL=∆MHN AL=HN
ΔALK~ΔLKM, LM=6LA
KN=KH+HM=
=LM+LA=18+3=21.
87.
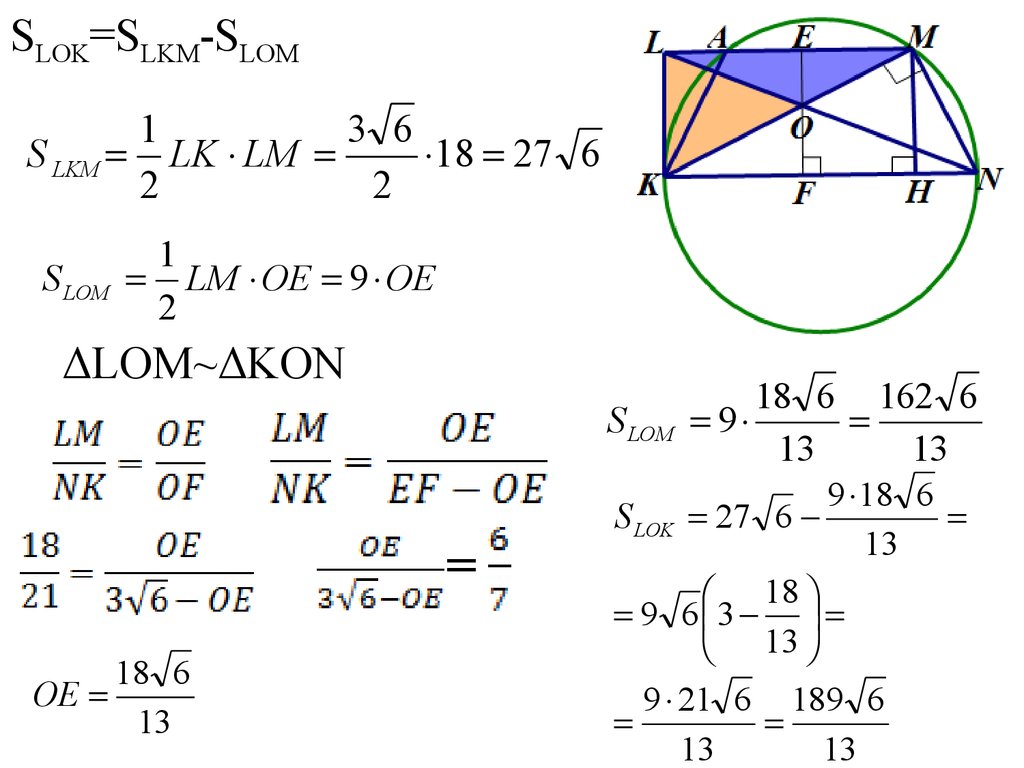
SLOK=SLKM-SLOM1
3 6
S LKM LK LM
18 27 6
2
2
S LOM
1
LM OE 9 OE
2
ΔLOM~ΔKON
S LOM
=
18 6
OE
13
18 6 162 6
9
13
13
9 18 6
S LOK 27 6
13
18
9 6 3
13
9 21 6 189 6
13
13
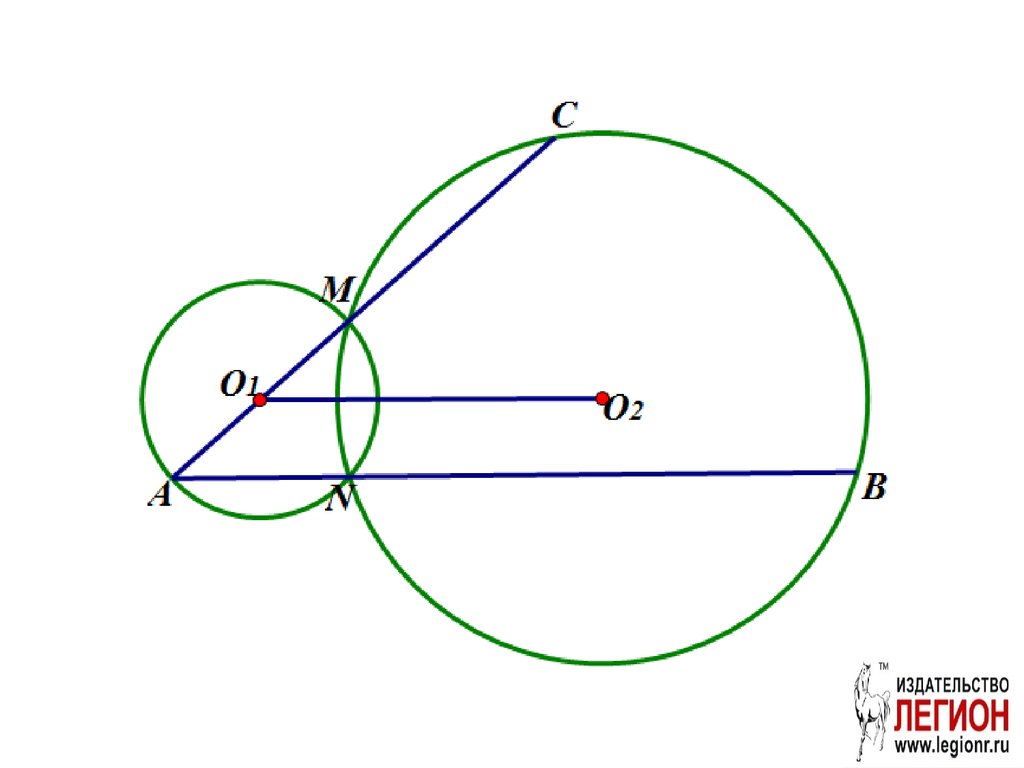
88. Задача (№16 вариант 15 «Легион» ЕГЭ 2018 )
Две окружности с центрами O1 и O2 пересекаются вточках M и N, причем точки O1 и O2 лежат по разные
стороны от прямой MN. Продолжение диаметра AM
первой окружности и хорды AN этой же окружности
пересекают вторую окружность в точках C и B
соответственно.
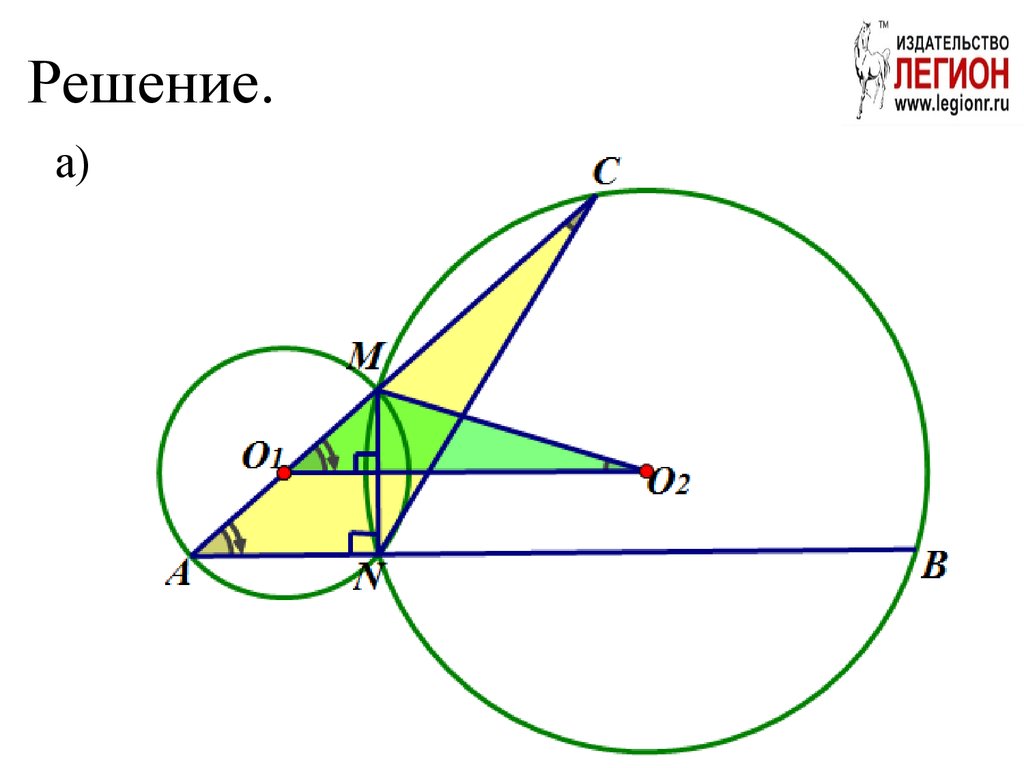
а) Докажите, что треугольники ANC и O1MO2 подобны;
б) Найдите MC, если ∠CMB= ∠NMA, а радиус второй
окружности в 2,5 раза больше радиуса первой и MN=2.
89.
90. Решение.
а)91. б)
MC=5
92.
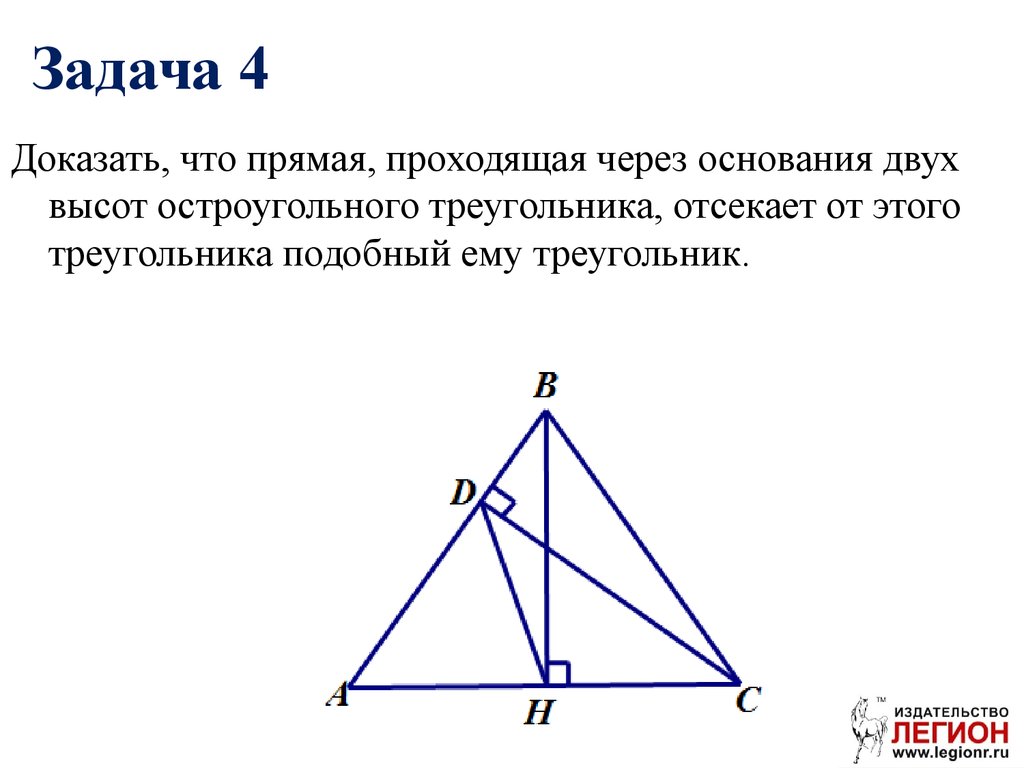
Задача 4Доказать, что прямая, проходящая через основания двух
высот остроугольного треугольника, отсекает от этого
треугольника подобный ему треугольник.
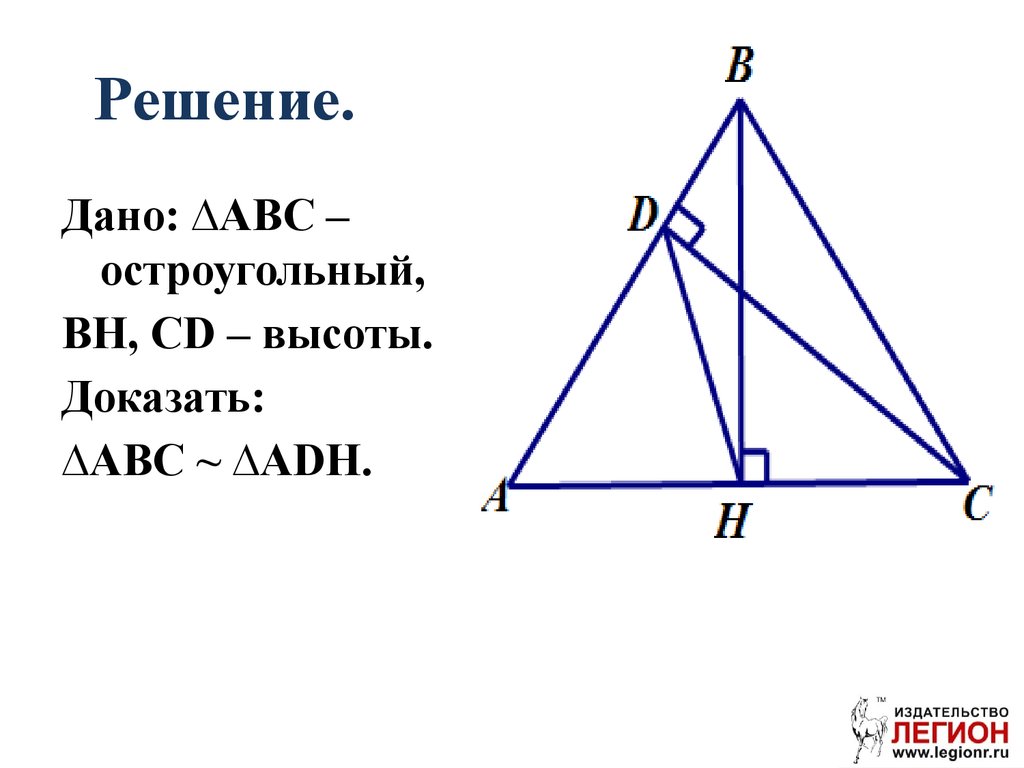
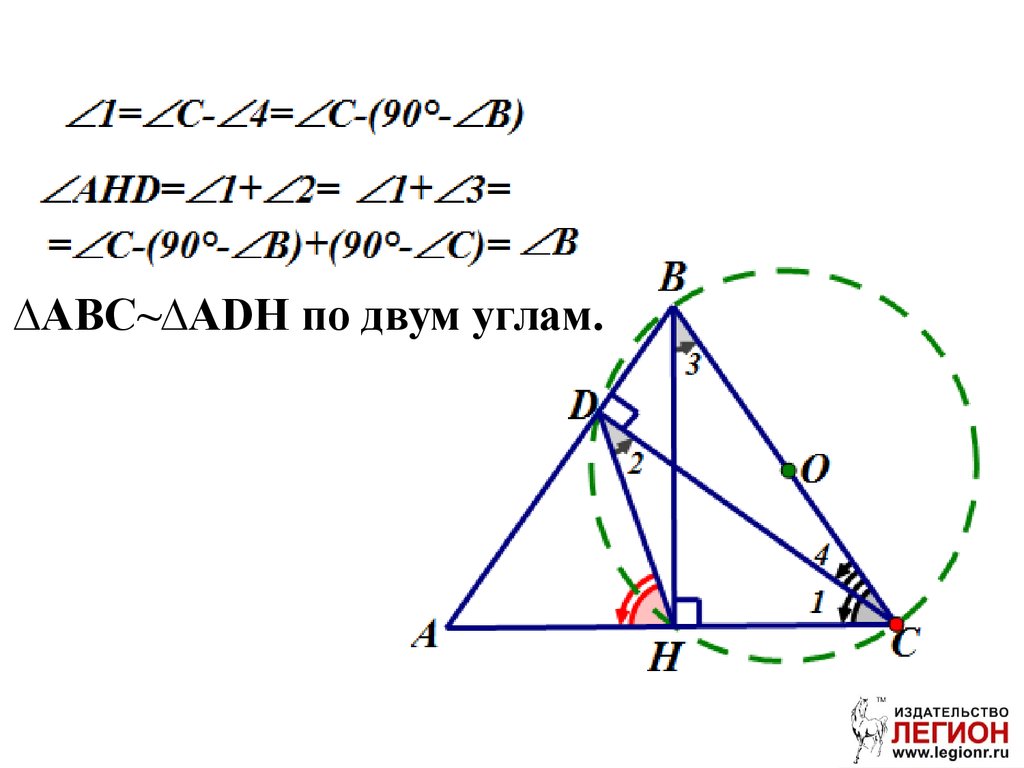
93. Решение.
Дано: ∆ABC –остроугольный,
BH, CD – высоты.
Доказать:
∆ABC ~ ∆ADH.
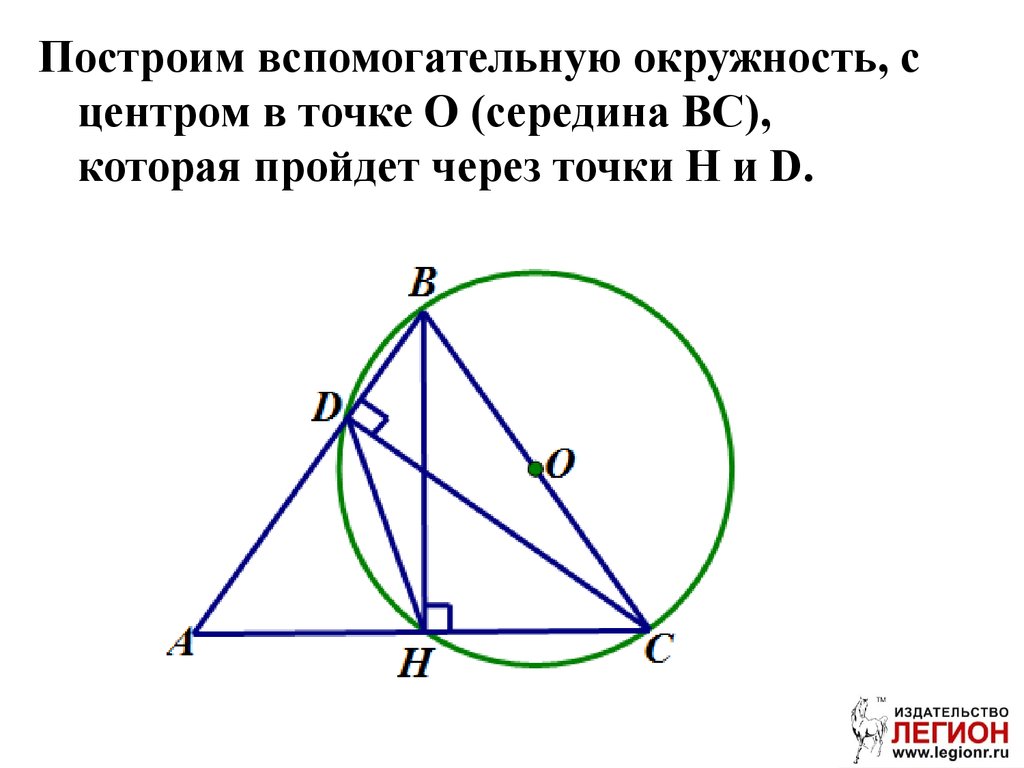
94.
Построим вспомогательную окружность, сцентром в точке О (середина ВС),
которая пройдет через точки H и D.
95.
∆ABC~∆ADH по двум углам.96. Задача
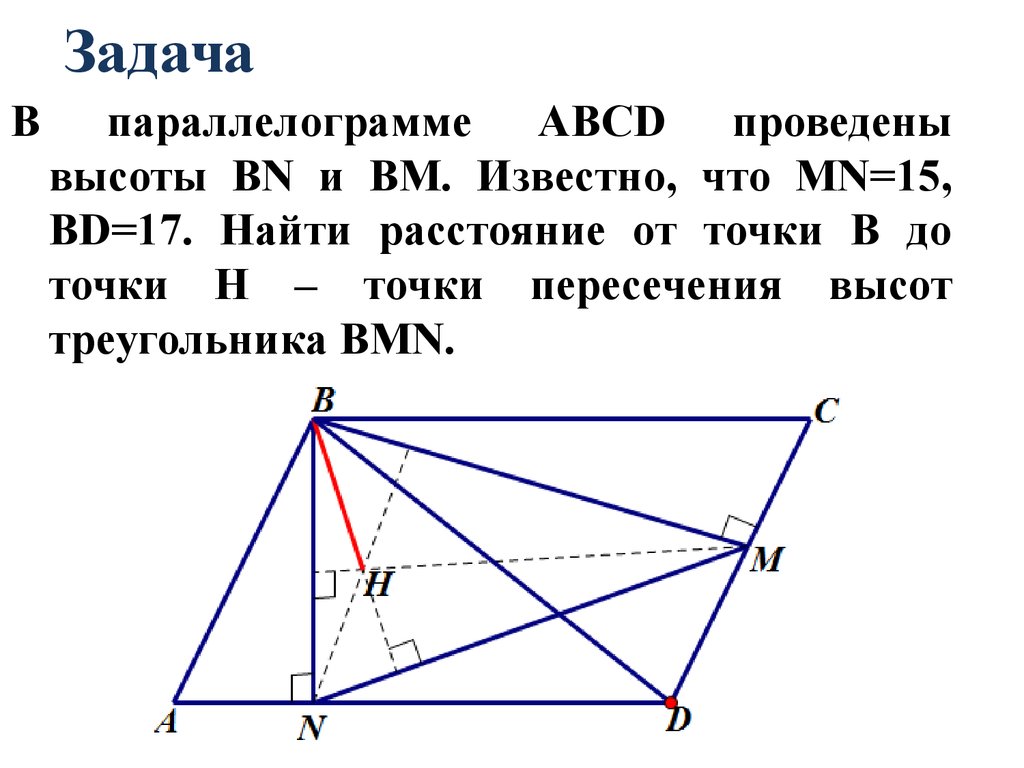
Впараллелограмме АВСD проведены
высоты ВN и ВМ. Известно, что МN=15,
ВD=17. Найти расстояние от точки В до
точки Н – точки пересечения высот
треугольника ВМN.
97.
Решение.BMN ~ BM 1 N1
BM 1 M 1 N1 BH
cos B
BM
MN
BD
M 1 N1 BH
15
17
15
M 1 N1 BH
17
M 1 N1
BH
sin B
15
sin B
17
BH 8
8
cos B
17
Ответ. 8
98. Задача
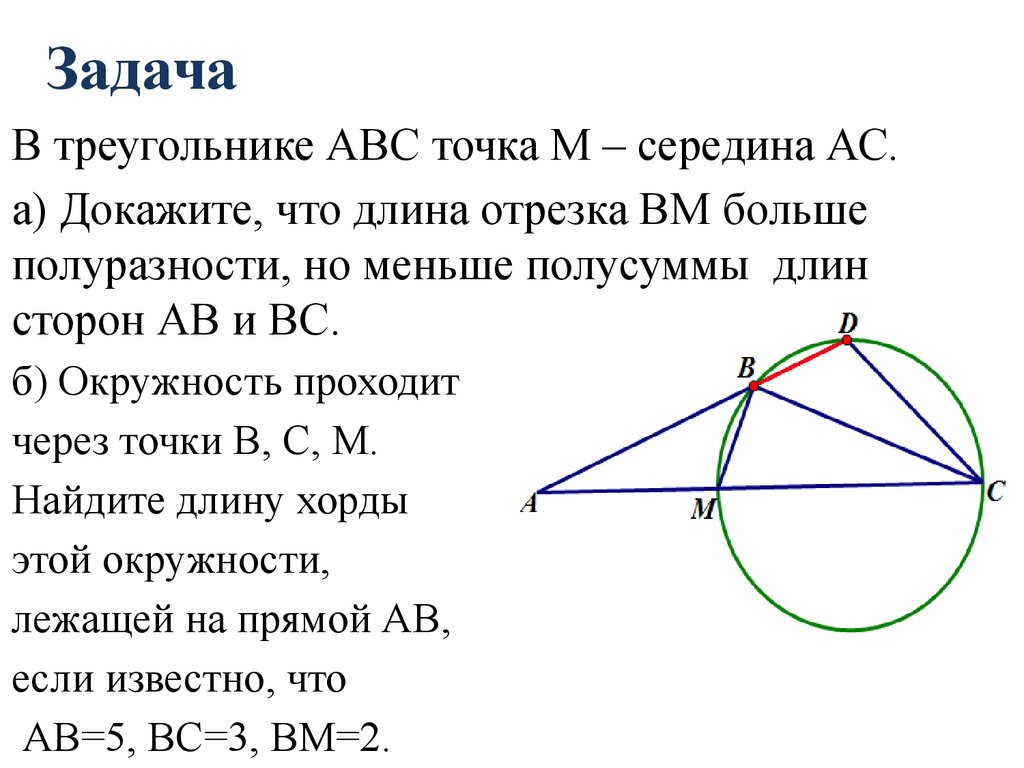
В треугольнике АВС точка М – середина АС.а) Докажите, что длина отрезка ВМ больше
полуразности, но меньше полусуммы длин
сторон АВ и ВС.
б) Окружность проходит
через точки В, С, М.
Найдите длину хорды
этой окружности,
лежащей на прямой АВ,
если известно, что
АВ=5, ВС=3, ВМ=2.
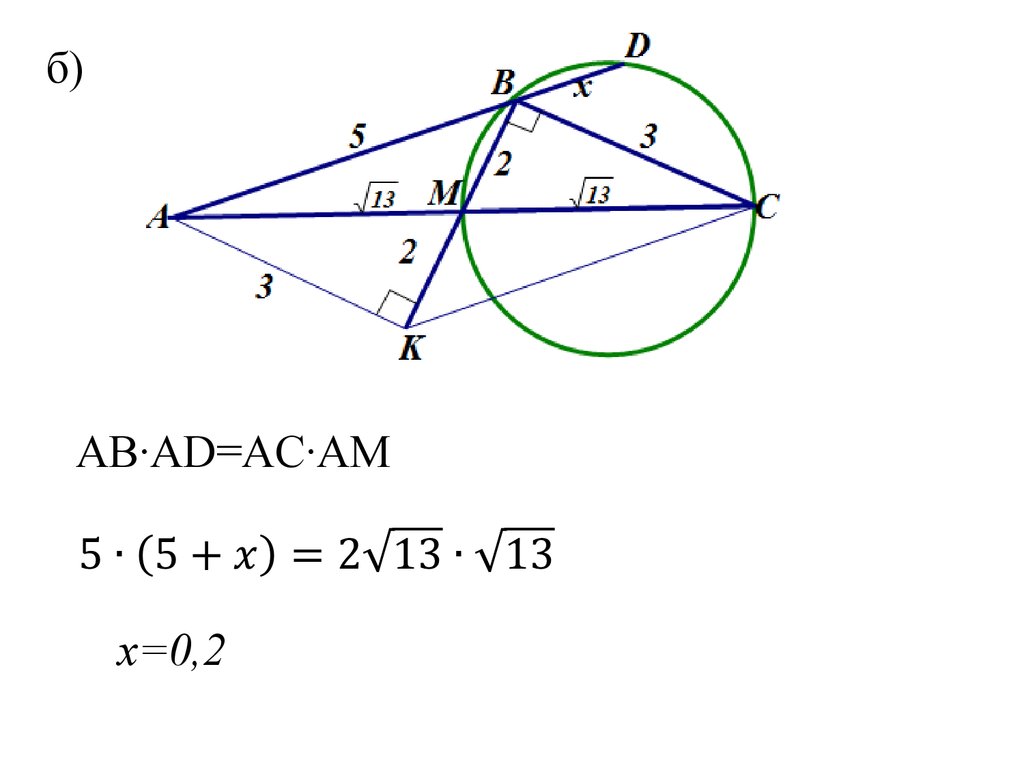
99. б)
AB·AD=AC·AMx=0,2






























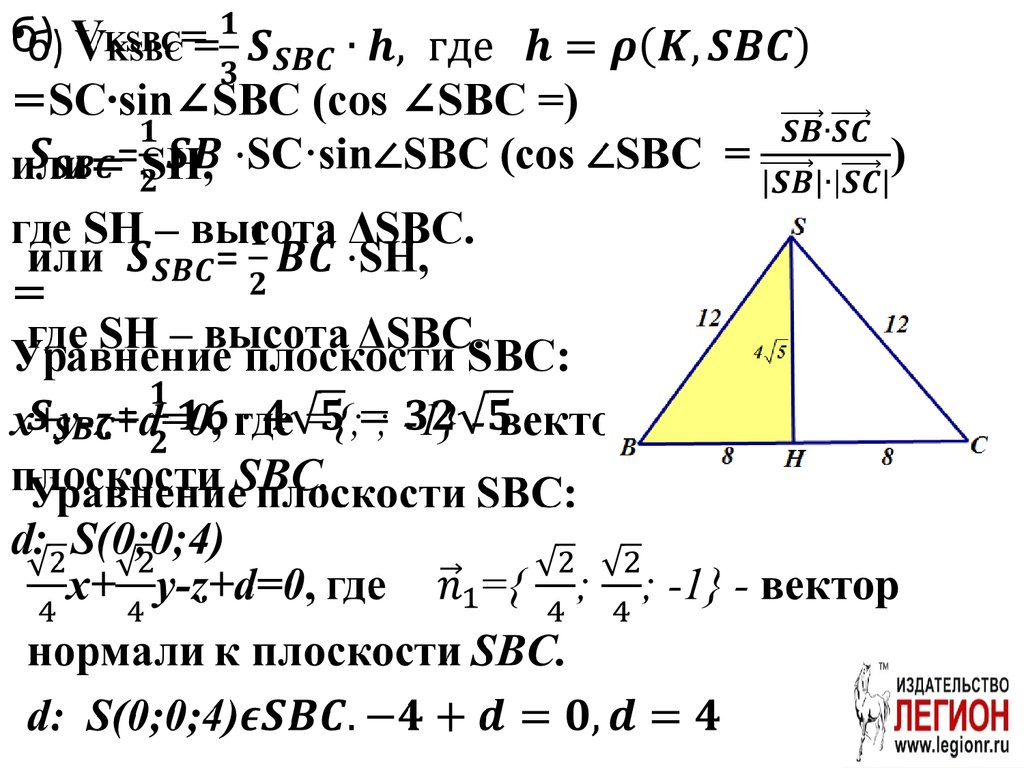
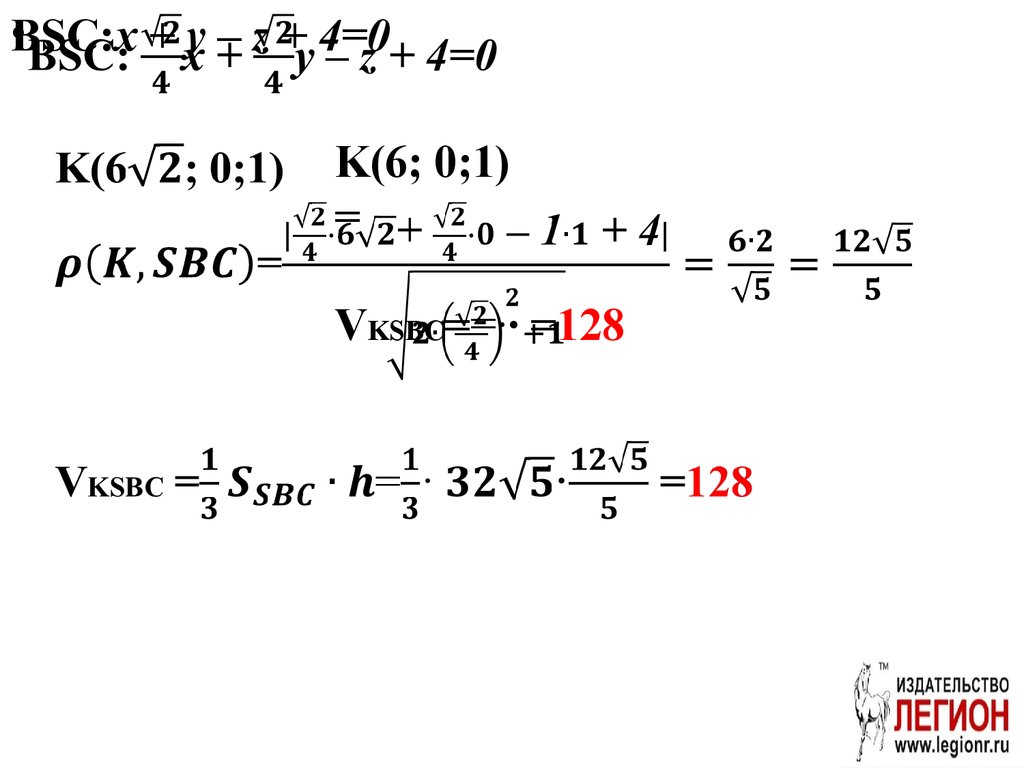









 mathematics
mathematics








