Решение задач 14 ЕГЭ

1. Решение задач 14 ЕГЭ

Попов Сергей 10 МБОУ «Ергачинская СОШ»
Руководитель: Кучукбаева Т.А.
20.12.2017

2. Цель проекта

• Научится решать задачи 14 части ЕГЭ различными
способами

3. Задачи

• Рассмотреть различные типы задач 14 ЕГЭ
• Рассмотреть различные способы решения задач 14 ЕГЭ

4. Типы задач

Расстояние между скрещивающимися прямыми
Расстояние от точки до прямой и до плоскости
Расстояние между плоскостями
Угол между прямой и плоскостью
Угол между плоскостями
Угол между скрещивающимися прямыми
Сечения многогранников
Объёмы многогранников
Первое полугодие
Второе полугодие

5. Нахождение расстояния от точки до прямой

6.

S
Аналитический
метод
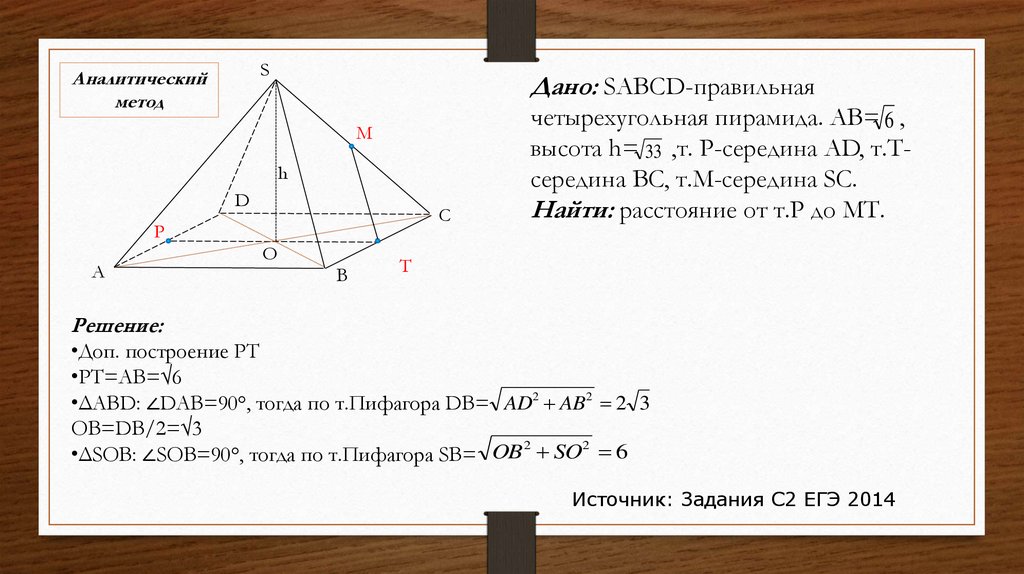
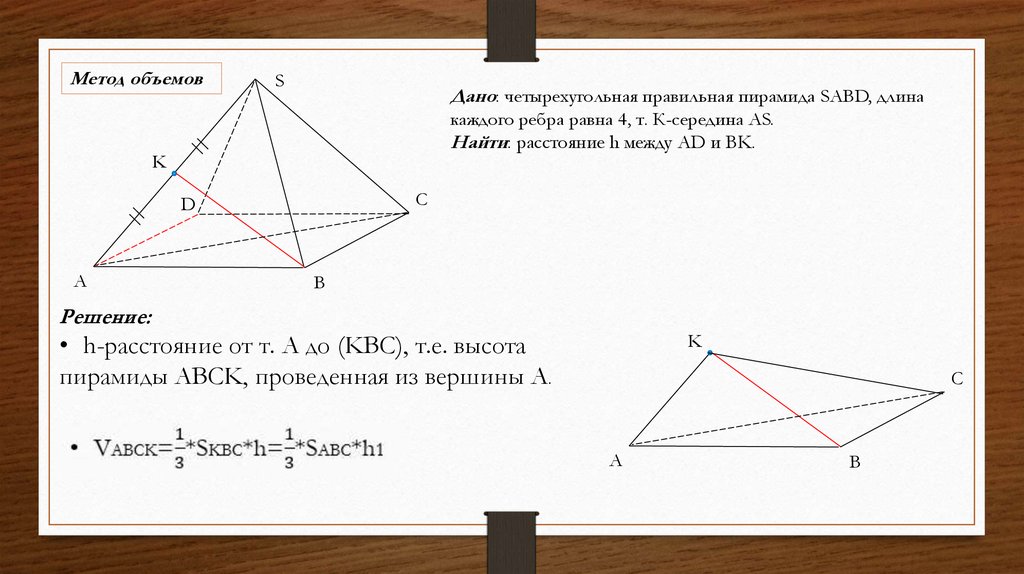
Дано: SABСD-правильная
M
h
D
C
P
A
О
B
четырехугольная пирамида. AB= 6 ,
высота h= 33 ,т. Р-середина AD, т.Тсередина BC, т.М-середина SC.
Найти: расстояние от т.Р до МТ.
T
Решение:
•Доп. построение PT
•PT=AB=√6
•ΔABD: ∠DAB=90°, тогда по т.Пифагора DB= AD2 AB2 2 3
OB=DB/2=√3
2
2
•ΔSOB: ∠SOB=90°, тогда по т.Пифагора SB= OB SO 6
Источник: Задания С2 ЕГЭ 2014

7.

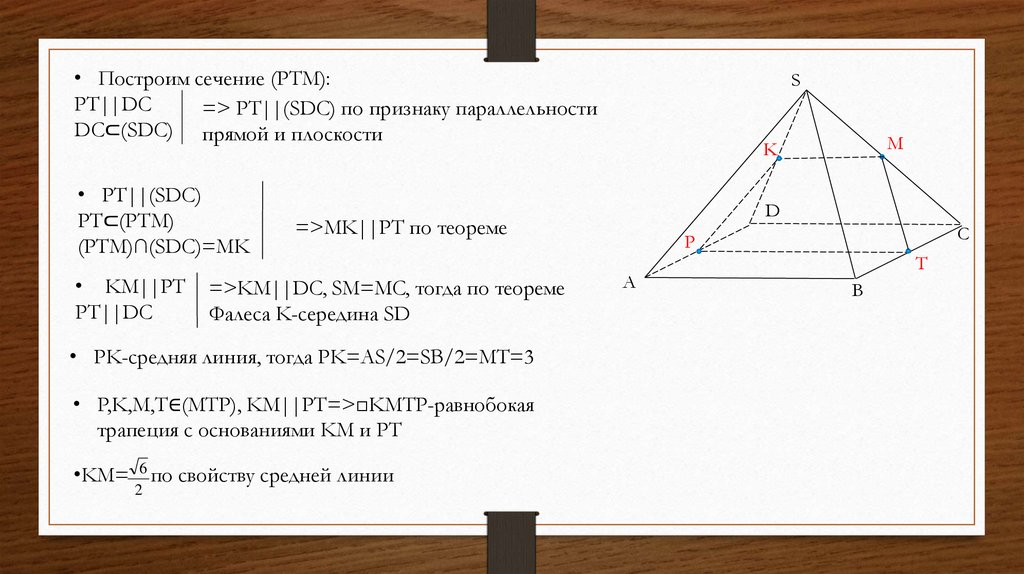
• Построим сечение (PTM):
PT||DC
=> PT||(SDC) по признаку параллельности
DC⊂(SDC) прямой и плоскости
• PT||(SDC)
PT⊂(PTM)
(PTM)∩(SDC)=MK
• KM||PT
PT||DC
=>KM||DC, SM=MC, тогда по теореме
Фалеса K-середина SD
• P,K,M,T∈(MTP), KM||PT=>□KMTP-равнобокая
трапеция c основаниями KM и PT
•KM= 6 по свойству средней линии
M
K
D
=>MK||PT по теореме
• PK-средняя линия, тогда PK=AS/2=SB/2=MT=3
2
S
С
P
A
T
B

8.

•Доп. построение KH и MF-высоты, KM=HF= 6
2
•ΔPKH=ΔMFT по двум катетам , тогда PH=FT=
√6
2
K
M
PT - HF
6
2
4
•ΔMFT, ∠MFT=90º, тогда по т.Пифагора MF= MT 2 FT 2
X
138
4
• Доп. построение PX┴ MT, PX-искомое расстояние
• SMPT=MF*PT/2
SMPT=PX*MT/2
=>MF*PT=PX*MT
138
* 6
MF
*
PT
23
4
•PX=
MT
3
2
Ответ:
23
2
P
H
6
F
T

9.

S
z
четырехугольная пирамида. AB=√6 ,
высота h= √33 ,т. Р-середина AD, т.Тсередина BC, т.М-середина SC.
Найти: расстояние от т.Р до МТ.
M ( 6 ; 3 6 ; 33 )
4 4
2
x
H (x;y;z)
D
C
(0;0;0) P
A
B
T (0;√6;0)
Решение:
• Поместим фигуру в систему координат
• Пусть PH-искомое расстояние, тогда PH * MT 0
• PH {x; y; z}; MT { 6 ; 6 ; 33 }
4
Дано: SABСD-правильная
Векторный метод
6
6
33
x
y
z 0
4
4
2
6 x 6 y 2 33 z 0
4
2
y

10.

6
3 6
33
6
6 33
x;
y;
z} MT { ;
;
}
4
4
2
4
4
2
6
3 6
x
y
4
4
, тогда x=√6-y
6
6
4
4
3 6
33
y
z
4
2
, тогда z=2√33- √22y
6
33
4
2
6 ( 6 y ) 6 y 2 33 (2 33 22 y ) 0
23 6
24
6
x
24
2 33
z
24
PH y 2 x 2 z 2
S
z
MH {
M
x
(
6 3 6 33
;
;
)
4 4
2
H (x;y;z)
D
C
(0;0;0) P
A
B
T (0;√6;0) y
y
Ответ :
23
2
6 x 6 y 2 33 z 0
23 * 23 * 6 6 33 * 4
23
24
2

11. Нахождение расстояния от точки до плоскости

12.

C1
Метод объемов
B1
D1
A1
K
X
P
D
Решение:
C
Q
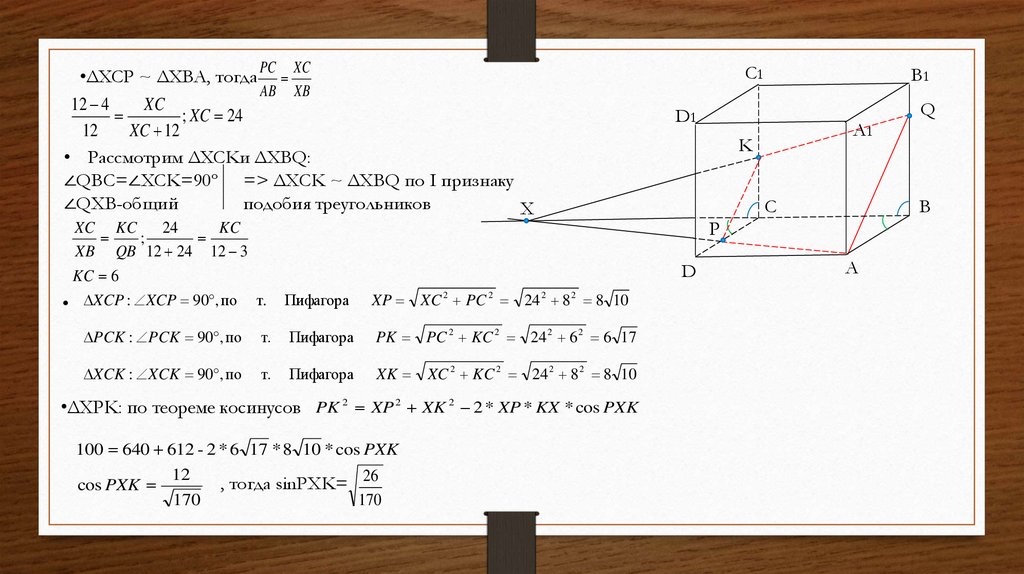
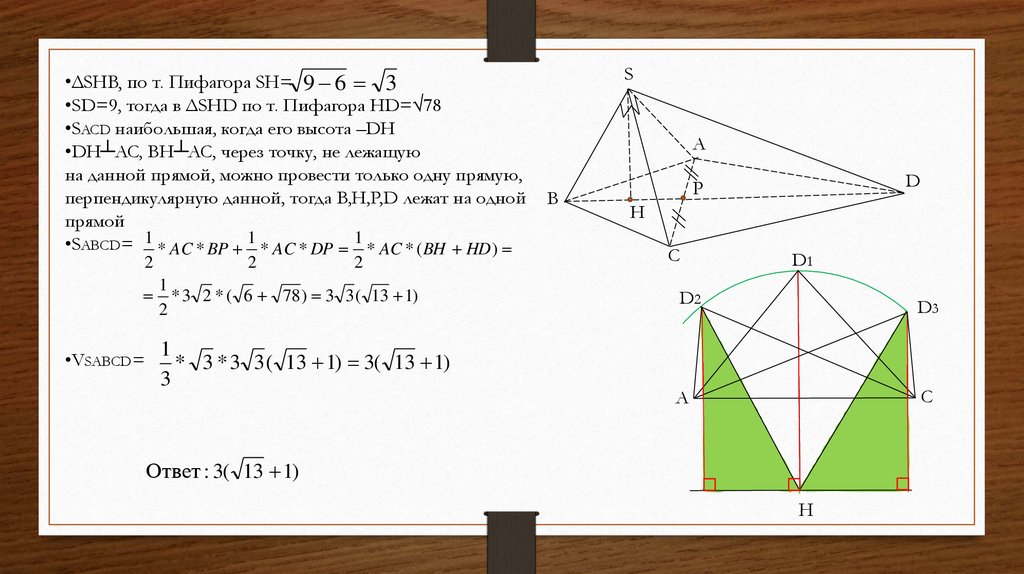
Дано: куб ABCDA1B1C1D1 со
стороной 12. т.P ∈ DC, DP=4, т.Q ∈
AB, B1Q=3.
Найти: расстояние h от т. С до (APQ).
B
A
VXPKC=SXKP*h/3=SXPC*KC/3
• Построим сечение (APQ):
• K,P,X ∈(APQ)=> искомое расстояние будет равно расстоянию от т. С до (XKP),
тогда h-высота тетраэдра KXPC, проведенная из вершины С.
• Рассмотрим ΔXCP и ΔXBA:
∠ABC=∠XCP=90º
=> ΔXCP ~ ΔXBA по Ι признаку подобия треугольников
∠AXB-общий
Источник: Задания 14 ЕГЭ 2016

13.

•ΔXCP ~ ΔXBA, тогда PC XC
AB XB
12 4
XC
; XC 24
12
XC 12
• Рассмотрим ΔXCKи ΔXBQ:
∠QBC=∠XCK=90º => ΔXCK ~ ΔXBQ по Ι признаку
подобия треугольников
∠QXB-общий
X
XC KC
24
KC
;
XB QB 12 24 12 3
KC 6
• XCP : XCP 90 , по т.
Пифагора
XP
PCK : PCK 90 , по
т.
Пифагора
PK PC 2 KC 2 24 2 6 2 6 17
XCK : XCK 90 , по
т.
Пифагора
XK
XC 2 PC 2 24 2 8 2 8 10
XC 2 KC 2 24 2 8 2 8 10
100 640 612 - 2 * 6 17 * 8 10 * cos PXK
12
170
, тогда sinPXK= 26
170
B1
D1
A1
K
C
Q
B
P
D
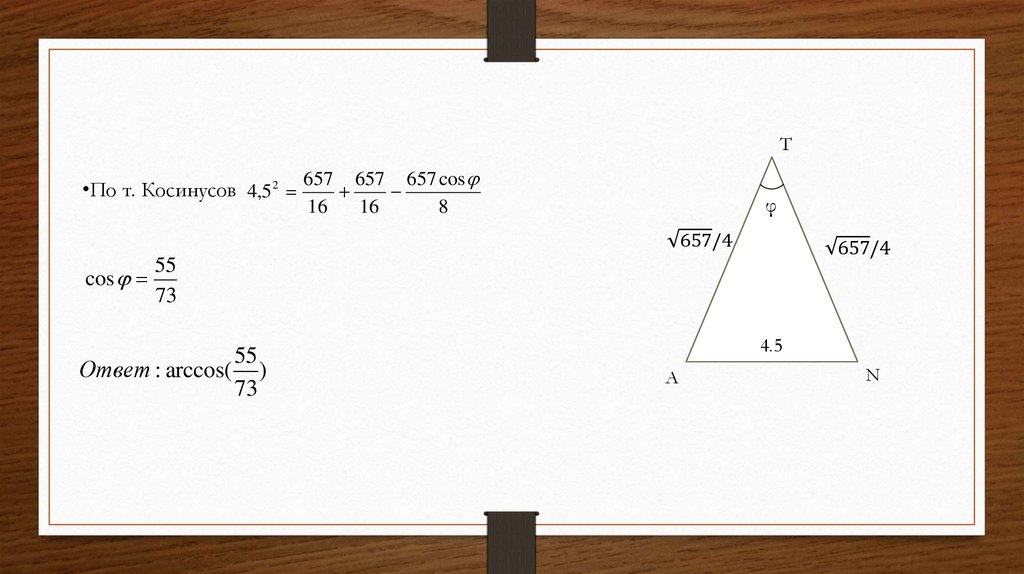
•ΔXPK: по теореме косинусов PK 2 XP 2 XK 2 2 * XP * KX * cos PXK
cos PXK
C1
A

14.

• SXKP=sinPXK*XK*XP/2
K
SXKP=
26
* 6 17 * 8 10 / 2 24 26
170
• SXPC=XC*PC/2=24*8/2=96
• VXPKC=SXKP*h/3=SXPC*KC/3
24 26 * h 96 * 6
12 26
13
12 26
Ответ :
13
h
X
C
P

15.

z
C1
D1
A1
(8;0;0) C (0;0;0)
P
x
D
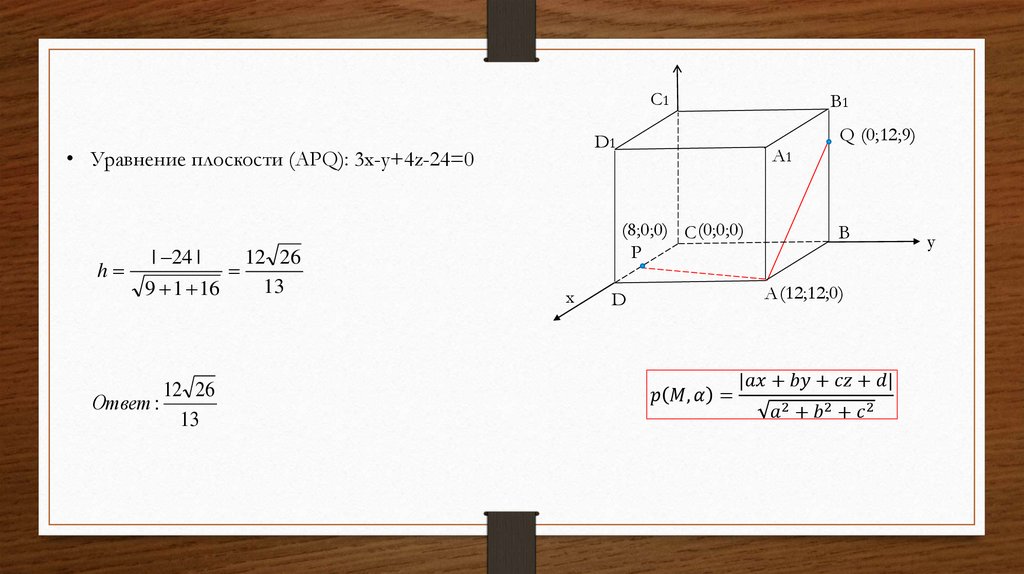
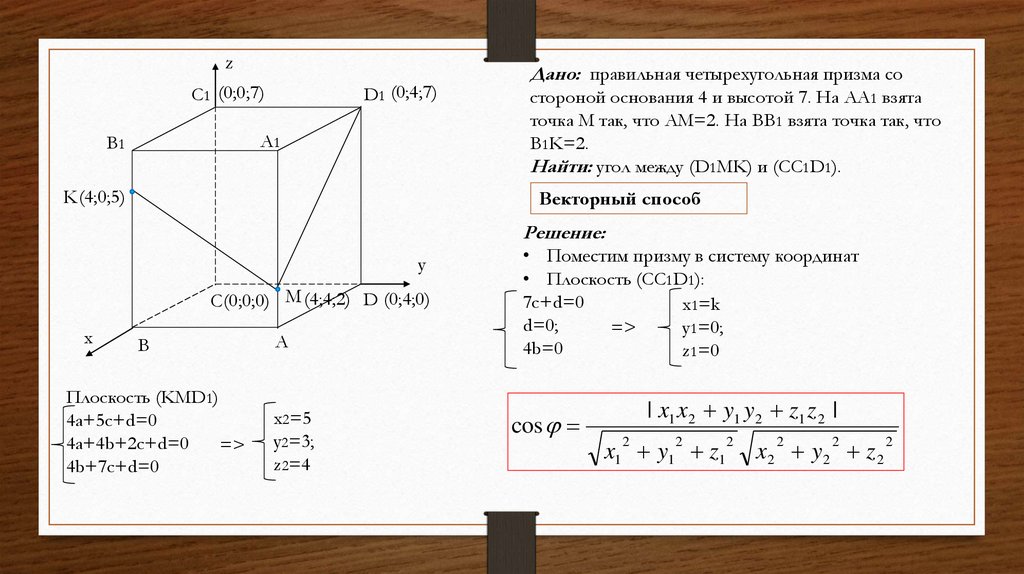
Дано: куб ABCDA1B1C1D1 со
B1
стороной 12. т.P ∈ DC, DP=4, т.Q ∈
AB, B1Q=3.
Найти: расстояние h от т. С до (APQ).
Q (0;12;9)
B
y
Метод координат
A (12;12;0)
• Поместим куб в систему координат
• Уравнение плоскости (APQ): ax+by+cz+d=0
8а+d=0
12a+12b+d=0 ;
12b+9c+d=0
ax -
ay 4az
8a 0
3
3
d=-8a
12a+12b-8a=0 ;
12b+9c-8a=0
d=-8a
b=-a/3 ;
-4a+9c-8a=0
d=-8a
b=-a/3
c=4a/3

16.

C1
D1
• Уравнение плоскости (APQ): 3x-y+4z-24=0
h
| 24 |
9 1 16
12 26
Ответ :
13
12 26
13
B1
A1
(8;0;0) C (0;0;0)
P
x
Q (0;12;9)
B
A (12;12;0)
D