Решение стереометрических задач методом координат. Построение сечений

1.

Решение стереометрических задач методом координат.
Построение сечений

2. Угол между прямыми

a x1 , y1 , z1
и b x2 , y2 , z 2 .
cos
a b
a b
x1 x2 y1 y2 z1 z 2
x12 y12 z12 x22 y22 z 22

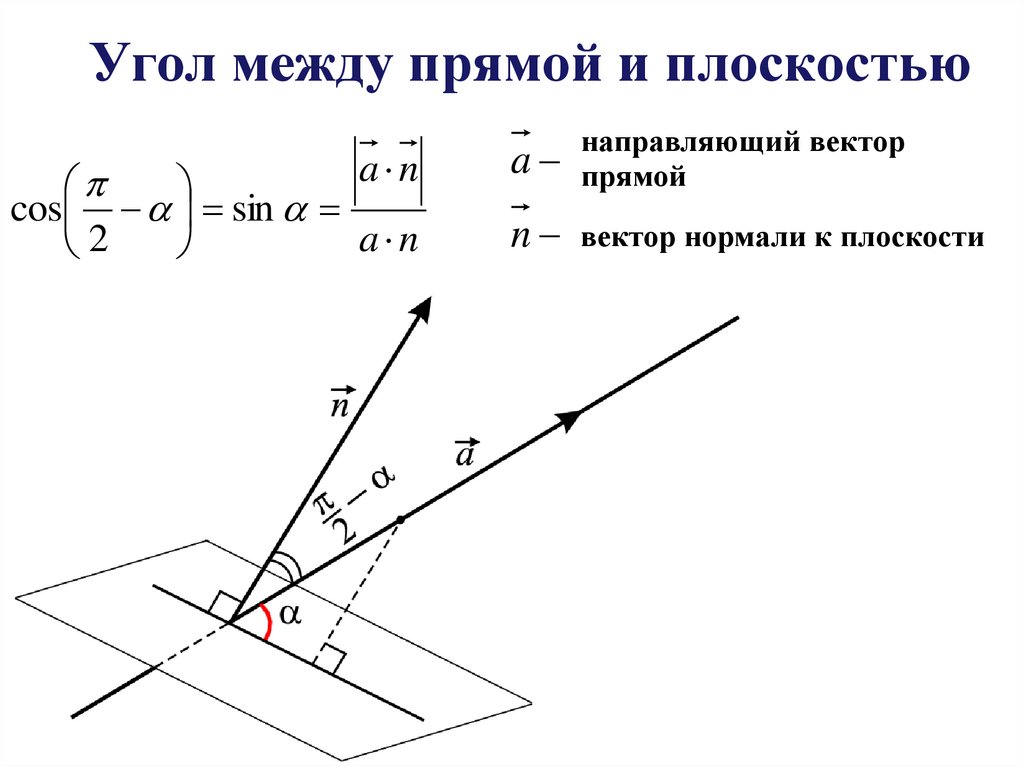
3. Угол между прямой и плоскостью

a n
cos sin
a n
2
a
направляющий вектор
прямой
n
вектор нормали к плоскости

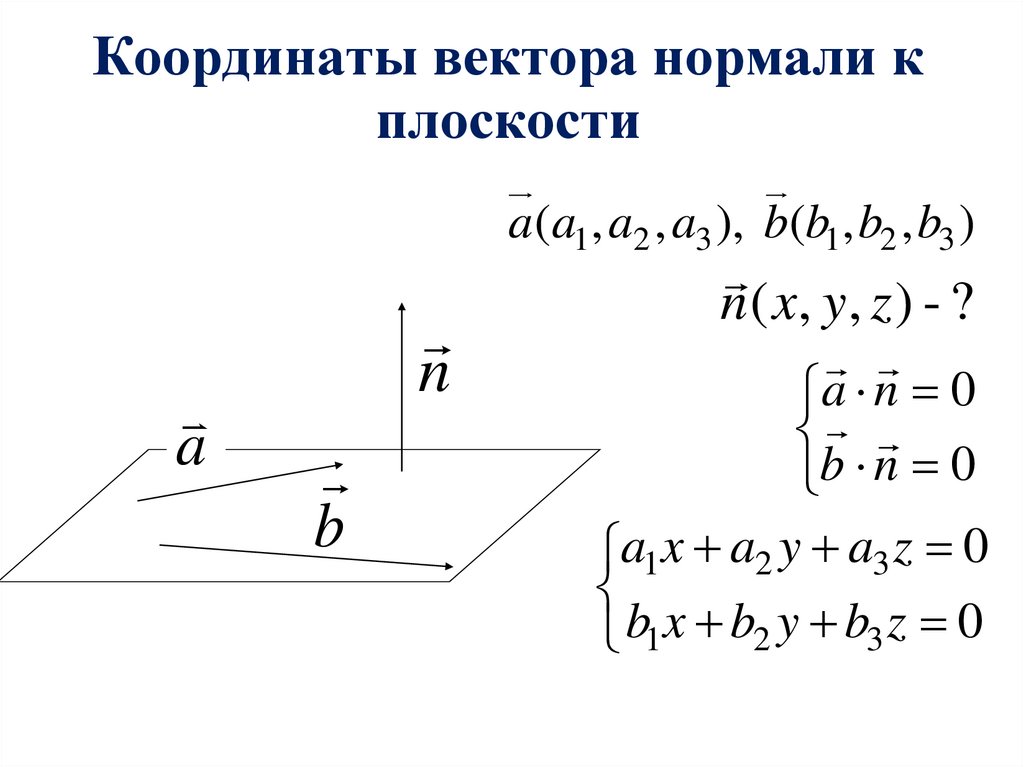
4. Координаты вектора нормали к плоскости

a(a1 , a2 , a3 ), b(b1 , b2 , b3 )
a
n
b
n ( x, y , z ) - ?
a n 0
b n 0
a1x a2 y a3 z 0
b1x b2 y b3 z 0

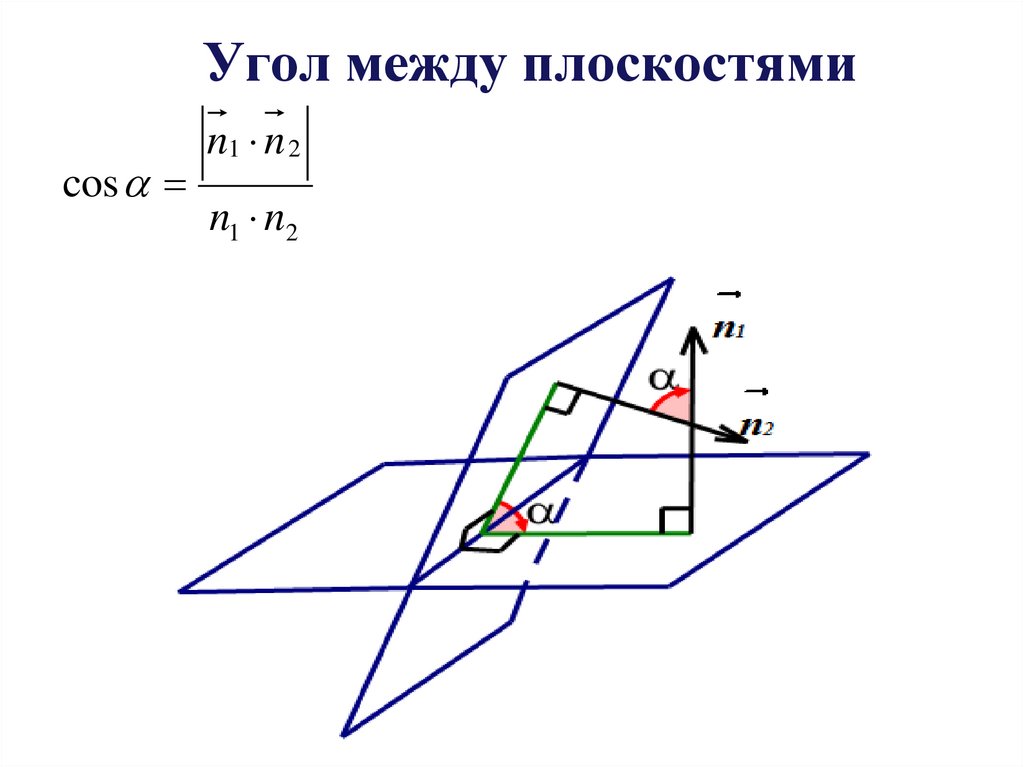
5. Угол между плоскостями

cos
n1 n 2
n1 n2

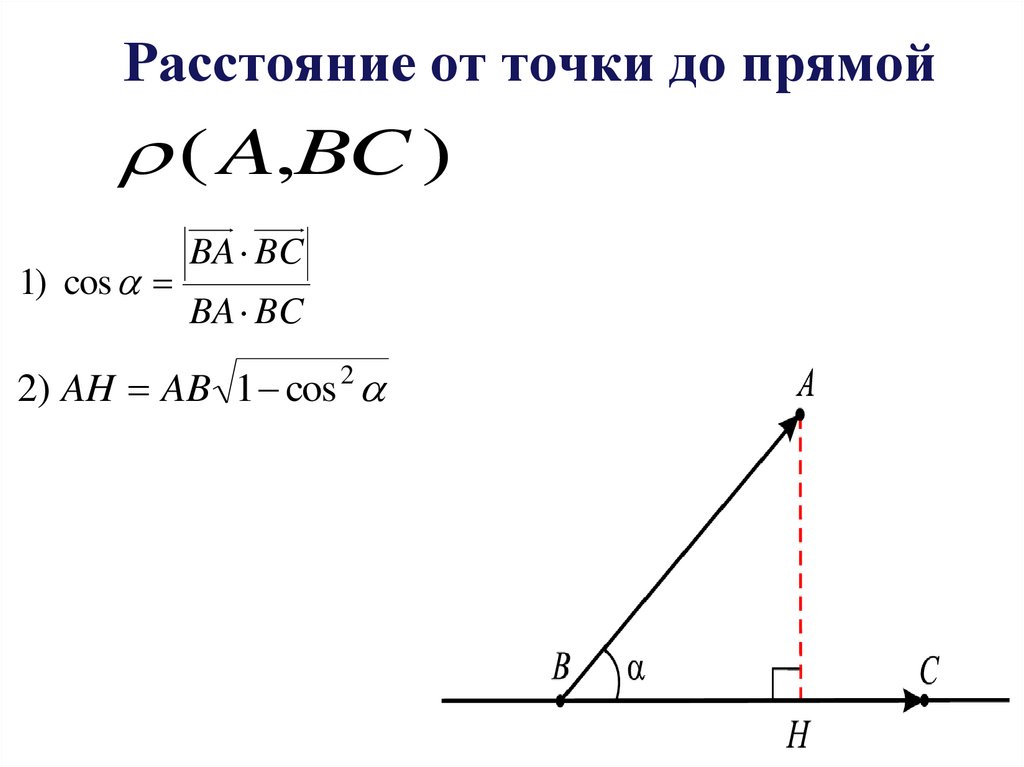
6. Расстояние от точки до прямой

( A,BC )
1) cos
BA BC
BA BC
2) AH AB 1 cos 2

7. Расстояние от точки до плоскости

ax0 by0 cz0 d
a b c
2
2
2
,
где x0 , y0 , z0 — координаты точки,
ax+by+cz+d=0
- уравнение
плоскости.

8. Расстояние между двумя скрещивающимися прямыми (метод координат)

Расстояние между двумя скрещивающимися прямыми
)
(метод координат
1) Классический метод — построение отрезка общего
перпендикуляра и нахождение его длины.
2) Проектирование.
3) Метод координат. Использование вспомогательной
плоскости.
4) Метод координат. Проекция на нормаль.
5) Векторный метод.

9.

Найти расстояние между скрещивающимися прямыми AB и CD.

10. Алгоритм

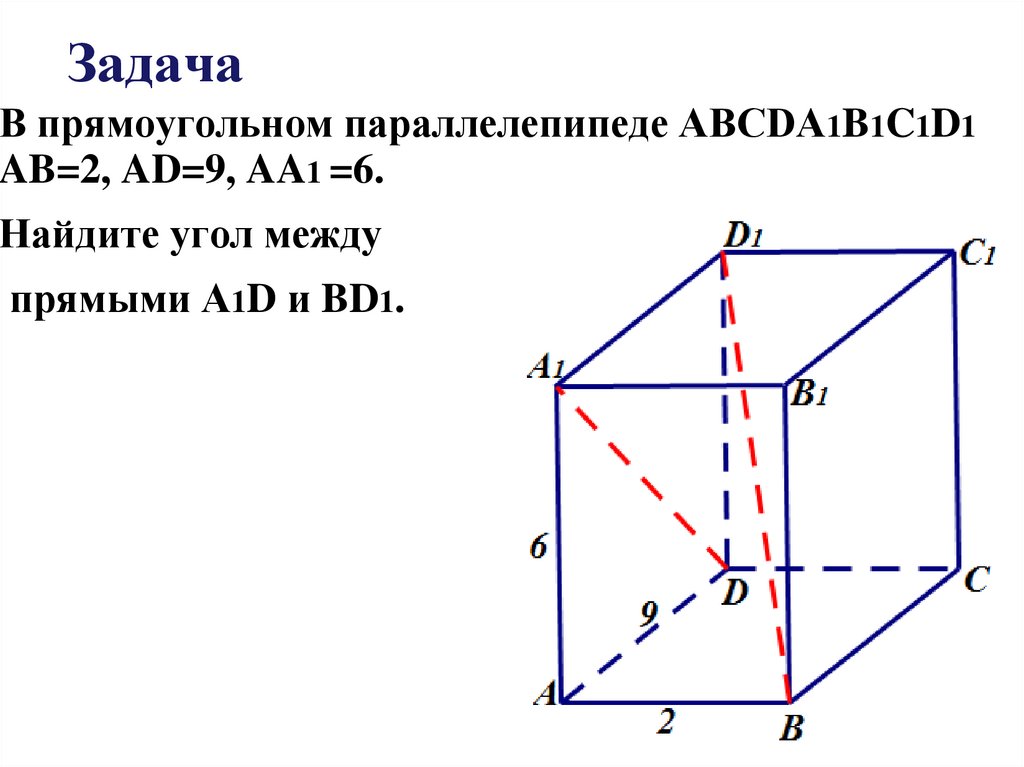
11. Задача

В прямоугольном параллелепипеде ABCDA1B1C1D1
AB=2, AD=9, AA1 =6.
Найдите угол между
прямыми A1D и BD1.

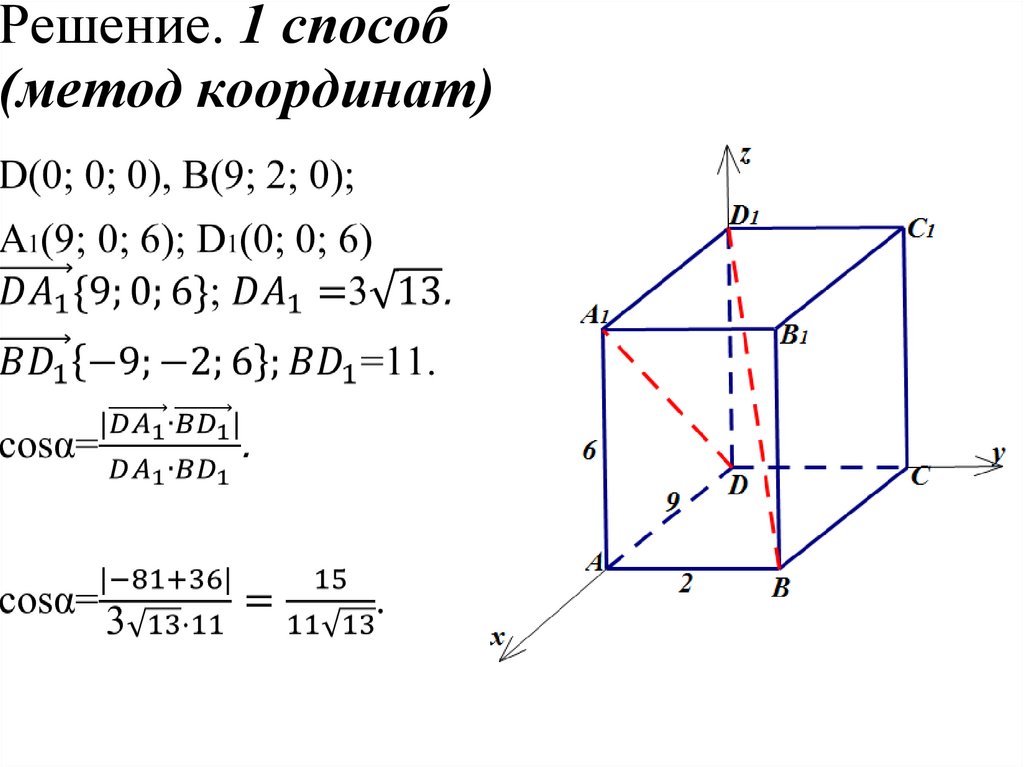
12. Решение. 1 способ (метод координат)

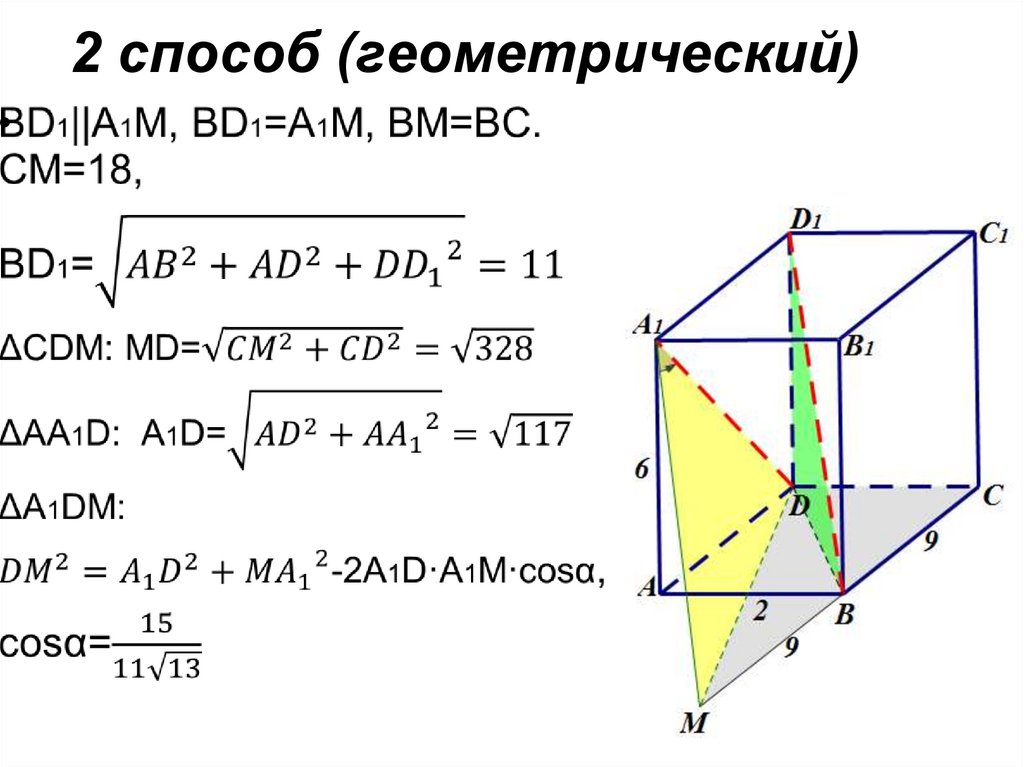
13. 2 способ (геометрический)

2 способ (геометрический)