Подобие треугольников

1.

ПОДОБИЕ
ТРЕУГОЛЬНИКОВ.
03.10.2018

2.

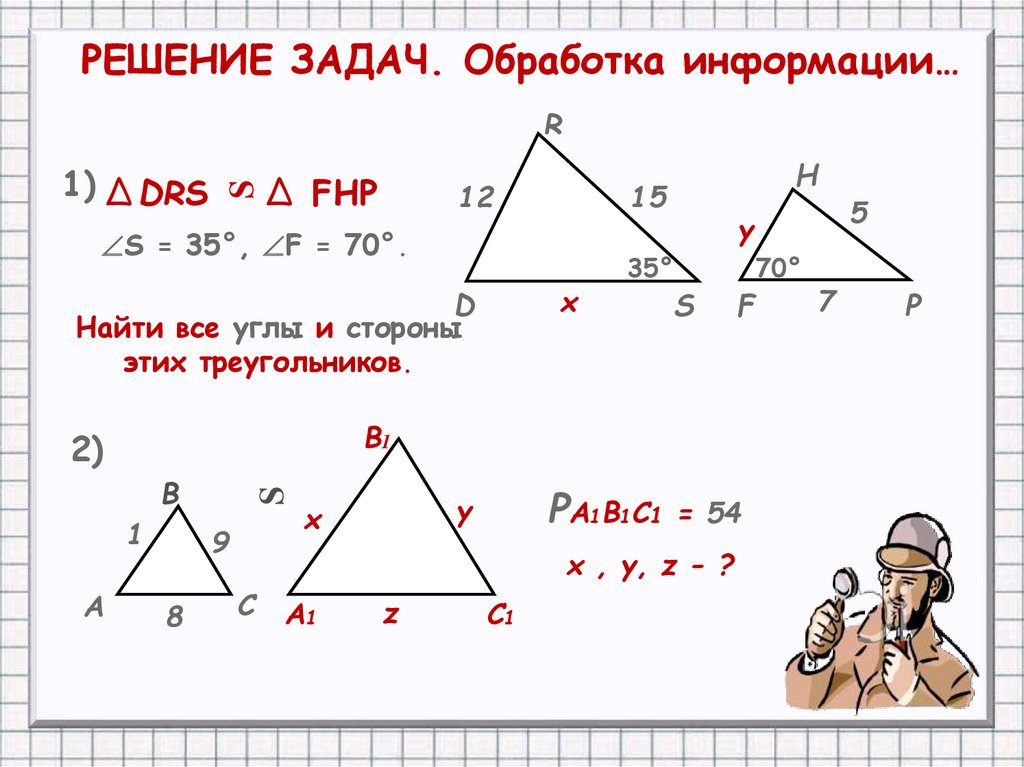
РЕШЕНИЕ ЗАДАЧ. Обработка информации…
R
S
1) Δ DRS
Δ FHP
12
15
S = 35°, F = 70°.
x
D
Найти все углы и стороны
этих треугольников.
y
35°
70°
S
F
B1
2)
1
S
B
А
H
9
8
PA1B1C1
y
x
= 54
х , y, z - ?
C
А1
z
C1
7
5
P

3.

Следствие продолжается…
3) Две стороны подобных треугольников
относятся как 2:5. Найти периметр
k? большего Δ,если периметр меньшего
Δ равен 16 см.
S

4.

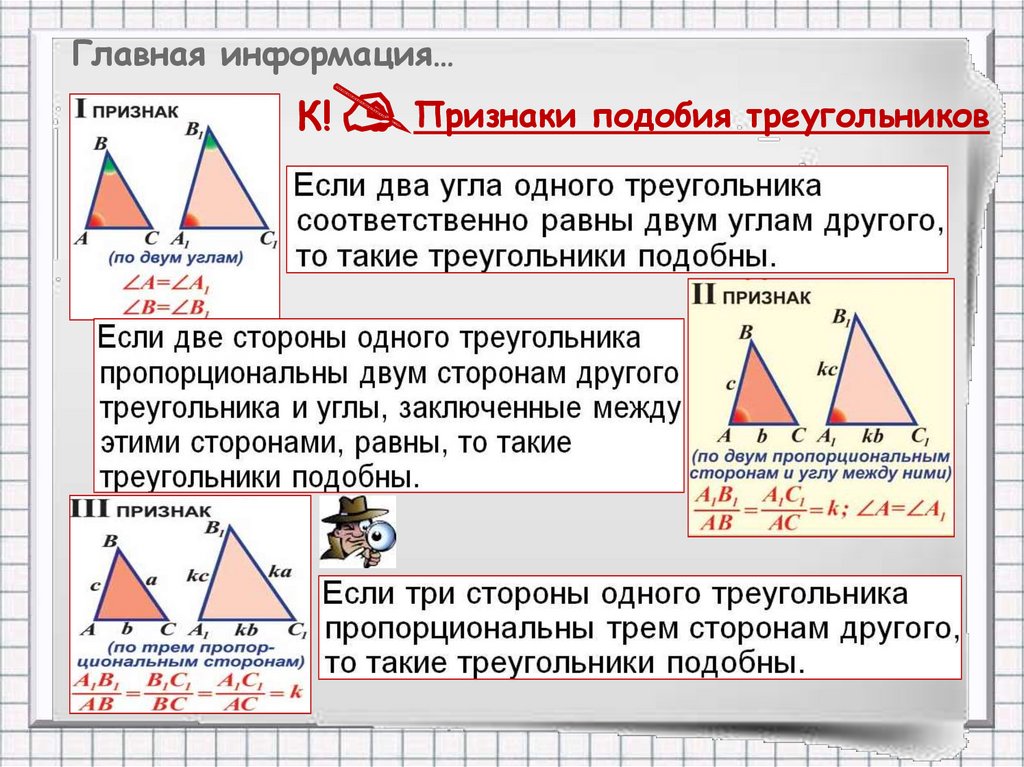
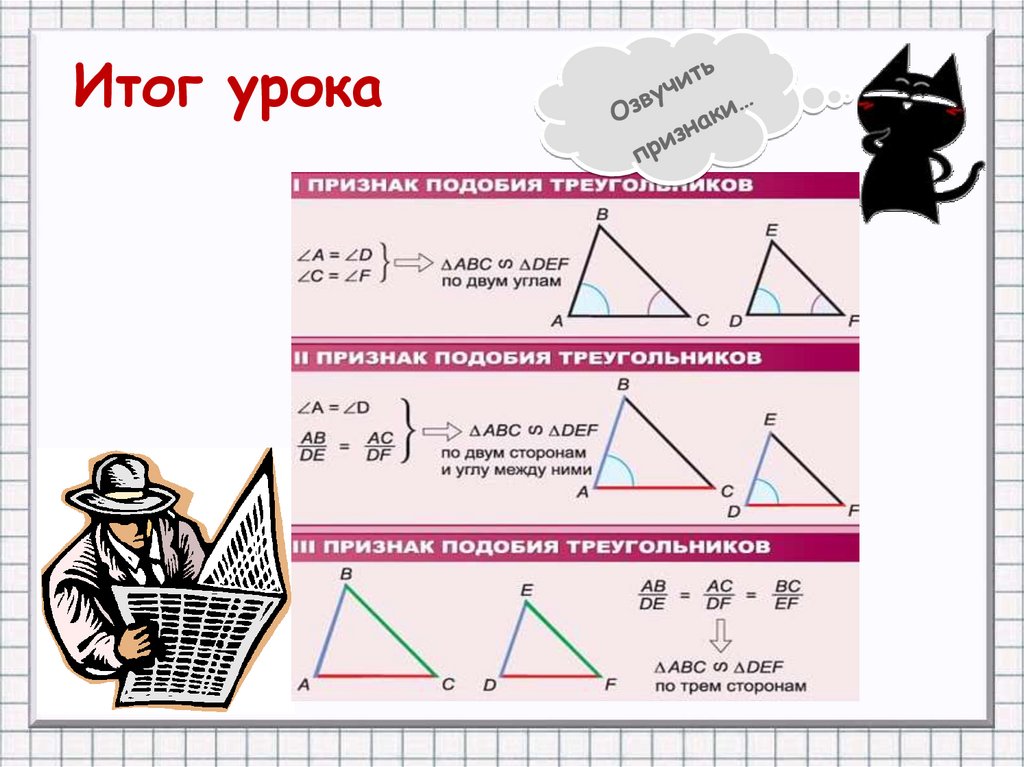
Главная информация…
К!
Признаки подобия треугольников

5.

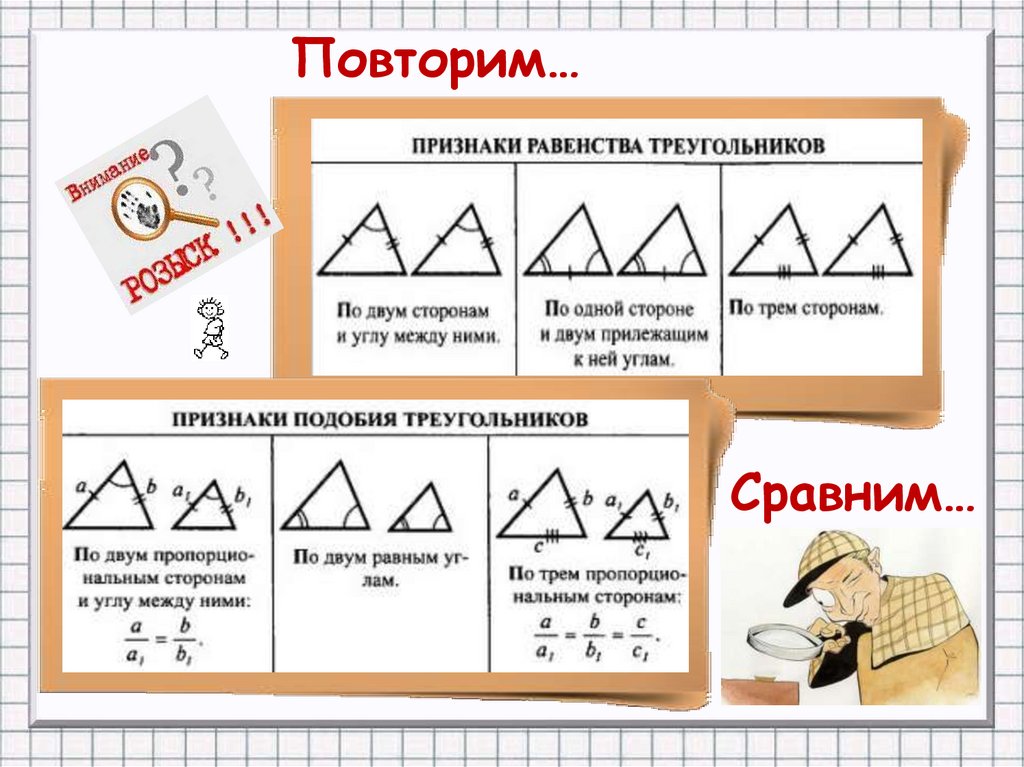
Повторим…
Сравним…

6. Подобие прямоугольных треугольников

Запомните!

7.

8.

Высота треугольника
Высота
прямоугольного
треугольника,
проведенная из вершины прямого угла,
разделяет треугольник на два подобных
прямоугольных треугольника, каждый из
которых подобен данному треугольнику. C
ABC ACD,
ABC CBD
ACD CBD
A
D
B

9. Определение

• Средним геометрическим
(пропорциональным) чисел a и b
называется квадратный корень из их
произведения.

10. Утверждение 1

1.Высота
прямоугольного
треугольника,
проведенная из вершины прямого угла, есть
среднее пропорциональное между отрезками, на
которые делится гипотенуза этой высотой
C
CD AD DB
A
D
B

11. Утверждение 2

2. Катет прямоугольного треугольника есть
среднее
пропорциональное
между
гипотенузой и проекцией этого катета на
гипотенузу.
C
AC AB AD ,
BC AB DB
A
D
B

12. Утверждение 3

• Биссектриса треугольника делит
противолежащую сторону на отрезки,
пропорциональные двум другим
сторонам

13.

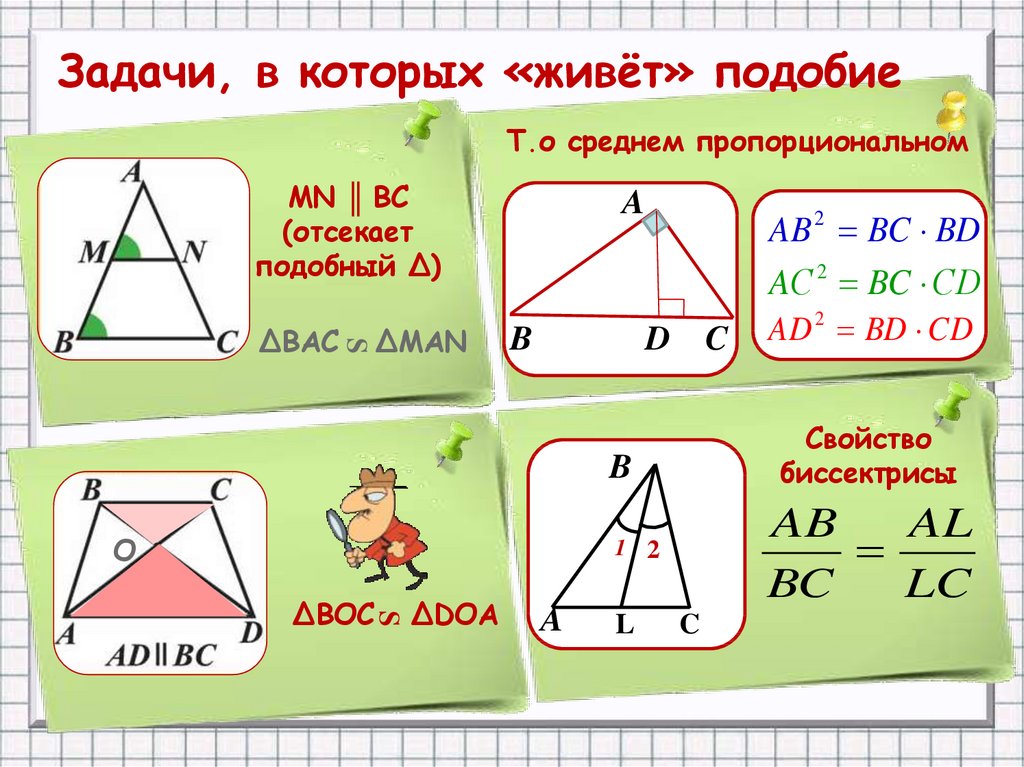
Задачи, в которых «живёт» подобие
Т.о среднем пропорциональном
MN ║ BC
(отсекает
подобный ∆)
∆MAN
S
∆BAC
A
B
AB 2 BC BD
AС 2 BC СD
D
C
Свойство
биссектрисы
B
O
AB
AL
BC
LC
1 2
S
∆BOC
∆DOA
A
L
AD 2 BD CD
C

14.

Итог урока

15.

Домашнее задание
• П.104, 105, 106 учить!
• Утверждения из п. 106 записать в
тетрадь
• Схему подобия на карточку
• № 38, 40, 44, 48*