Similar presentations:
Средняя линия трапеции (несколько способов доказательства)
1. МАТЕМАТИКА Средняя линия трапеции (несколько способов доказательства)
2.
Объект исследования: трапеция, средняя линия трапеции.Цель: показать, что доказательство теоремы о средней линии
трапеции с помощью векторов, приведённое в учебнике
Л.С. Атанасяна «Геометрия 7-9 классы» не является единственным,
что существуют и другие способы доказательства.
Задачи:
1. Изучение научной и учебной литературы по заданной теме.
2. Привести другие способы доказательства теоремы о средней
линии трапеции.
3. При доказательстве этой теоремы показать значение других
теорем: признаков равенства треугольников, теоремы о
параллельности
прямых,
теоремы
о
средней
линии
треугольника, а также следствие из аксиомы параллельных
прямых, и определение средней линии треугольника и средней
линии трапеции, признаки и определение параллелограмма.
Методы
исследования:
применение
аналитического
синтетического методов доказательства теорем.
и
2
3.
А можно лидоказать?
Исходная теорема
называется прямой
теоремой
Обратная теорема если
в
исходной
теореме
условие
сделать заключением, а
заключение – условием.
Теорема – математическое утверждение,
истинность которого установлена путем
доказательства [3].
Доказательством называется
конечная последовательность
формул, каждая из которых либо
является аксиомой, либо
получается из некоторых
предыдущих формул этой
последовательности по одному
из правил вывода [3].
Взаимно обратные
теоремы - если верны
прямая и обратная
теоремы
Если верна прямая
теорема, то обратная
теорема может быть
неверной
Классическая теорема
состоит из двух частей:
из условия и заключения.
Условие обыкновенно
начинается со слова
«если», а заключение со
слова «то».
3
4.
Теоретическая частьСредней линией треугольника называется отрезок, соединяющей
середины двух его сторон.
Средней линией трапеции называется отрезок, соединяющий
середины ее боковых сторон.
Параллелограммом называется четырехугольник, у которого
противоположные стороны попарно параллельны.
Два угла называются вертикальными, если
стороны одного угла являются продолжением
сторон другого. 1и 2; 3и 4
вертикальные.
Свойство вертикальных углов. Вертикальные углы равны
Прямые a и b параллельны, с –секущая.
Пары углов: 1и 2; 3и 4
называются накрест лежащими.
4
5.
Следствие 2° из аксиомы параллельных. Если две прямыепараллельны третьей прямой, то они параллельны.
Теорема о средней линии треугольника. Средняя линия
треугольника параллельна одной из его сторон и равна половине этой
стороны.
Второй признак равенства треугольников. Если сторона и два
прилежащие к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то
такие треугольники равны.
Признак параллельности двух прямых. Если при пересечении двух
прямых секущей накрест лежащие углы равны, то прямые
параллельны.
Признак параллелограмма 1°. Если в четырехугольнике две стороны
равны и параллельны, то этот четырехугольник параллелограмм.
5
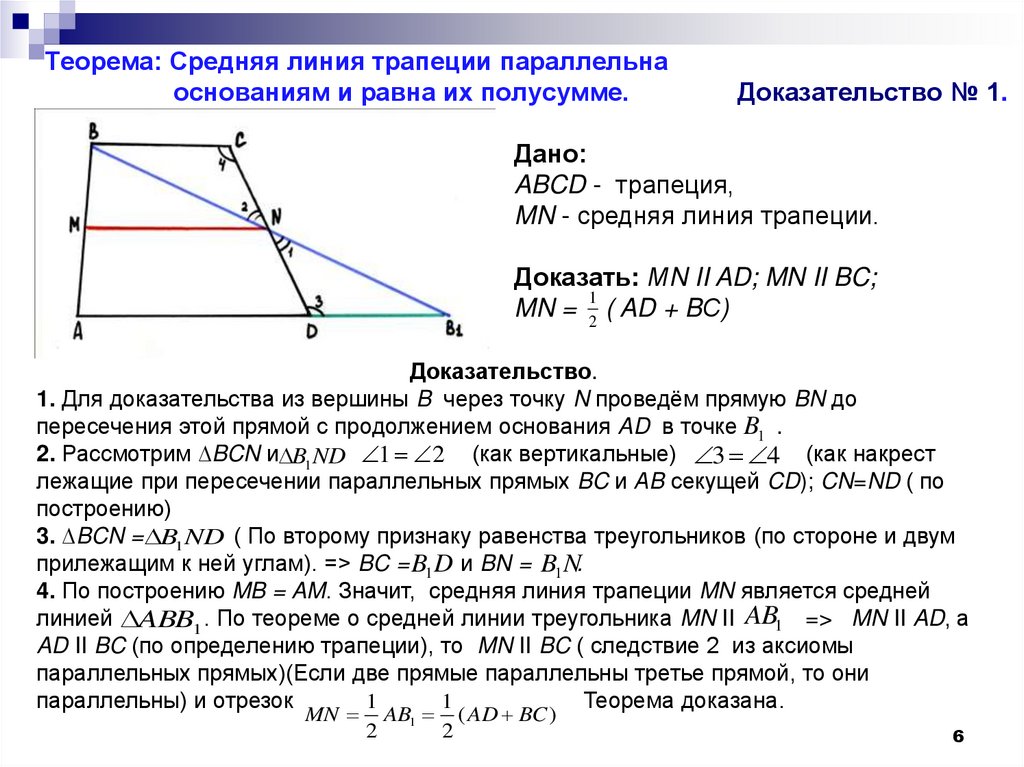
6. Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 1.
Дано:ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства из вершины B через точку N проведём прямую BN до
пересечения этой прямой с продолжением основания AD в точке B1 .
2. Рассмотрим ∆BCN и B1 ND 1 2 (как вертикальные) 3 4 (как накрест
лежащие при пересечении параллельных прямых BC и АB секущей CD); CN=ND ( по
построению)
3. ∆BCN = B1 ND ( По второму признаку равенства треугольников (по стороне и двум
прилежащим к ней углам). => BC = B1 D и BN = B1 N.
4. По построению MB = AM. Значит, средняя линия трапеции MN является средней
линией ABB1 . По теореме о средней линии треугольника MN II AB1 => MN II AD, а
AD II BC (по определению трапеции), то MN II BC ( следствие 2 из аксиомы
параллельных прямых)(Если две прямые параллельны третье прямой, то они
1
1
параллельны) и отрезок
Теорема доказана.
MN
2
AB1
2
( AD BC )
6
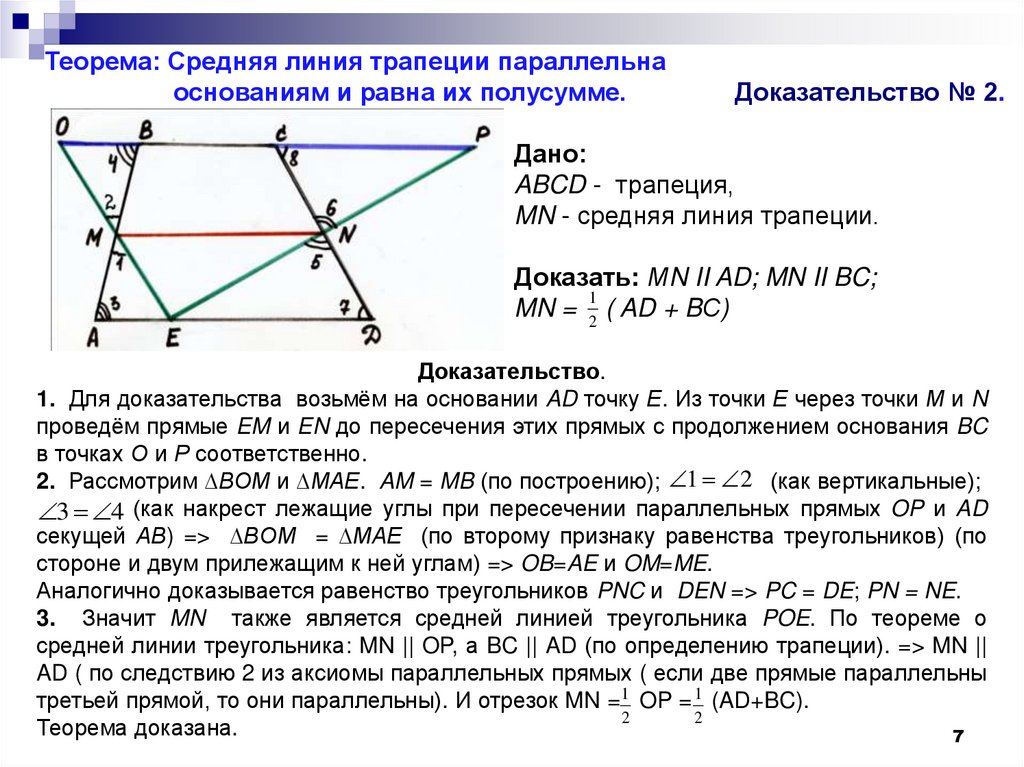
7.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 2.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства возьмём на основании AD точку Е. Из точки Е через точки М и N
проведём прямые EM и EN до пересечения этих прямых с продолжением основания BC
в точках О и Р соответственно.
2. Рассмотрим ∆BOM и ∆MAE. AM = MB (по построению); 1 2 (как вертикальные);
3 4 (как накрест лежащие углы при пересечении параллельных прямых OP и AD
секущей АВ) => ∆BOM = ∆MAE (по второму признаку равенства треугольников) (по
стороне и двум прилежащим к ней углам) => OB=AE и OM=ME.
Аналогично доказывается равенство треугольников PNC и DEN => PC = DE; PN = NE.
3. Значит MN также является средней линией треугольника POE. По теореме о
средней линии треугольника: MN || OP, а BC || AD (по определению трапеции). => MN ||
AD ( по следствию 2 из аксиомы параллельных прямых ( если две прямые параллельны
третьей прямой, то они параллельны). И отрезок MN = 1 OP = 1 (AD+BC).
2
2
Теорема доказана.
7
8.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 3.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. На основании BC возьмём произвольную точку Е. Из точки Е через точки М и N
проведём прямые EM и EN до пересечения этих прямых с продолжением основания AD
в точках O и Р соответственно.
2. Рассмотрим ∆МВЕ и ∆АОМ. 1 2 (как вертикальные); 3 4 (как накрест
лежащие углы при пересечении параллельных прямых ВС и ОР секущей АВ); АМ=МВ
(по построению). => ∆МВЕ =∆АОМ (по второму признаку равенства треугольников (по
стороне и двум прилежащим к ней углам) => ВЕ=ОА и ЕМ = ОМ. Аналогично
доказывается равенство треугольников СЕN и PND => EN=NP и EC=PD.
3. Значит MN также является средней линией треугольника POE. По теореме о средней
линии треугольника MN || OP => MN || AD, а AD || BC (по определению трапеции) =>
MN || BC (по следствию 2 из аксиомы параллельных прямых (если две прямые
параллельны третьей прямой, то они параллельны) и отрезок
1
1
1
Теорема доказана.
8
MN OA AD DP OP AD BC
2
2
2
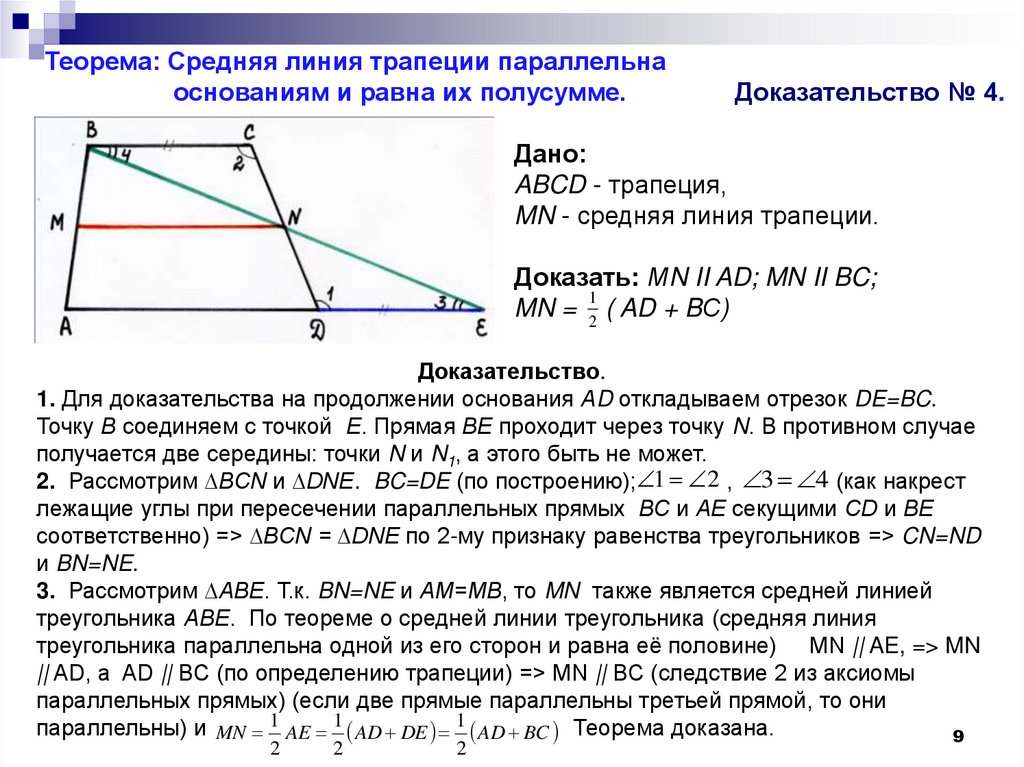
9.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 4.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства на продолжении основания АD откладываем отрезок DE=BC.
Точку В соединяем с точкой Е. Прямая ВЕ проходит через точку N. В противном случае
получается две середины: точки N и N1, а этого быть не может.
2. Рассмотрим ∆BCN и ∆DNE. BC=DE (по построению); 1 2 , 3 4 (как накрест
лежащие углы при пересечении параллельных прямых ВС и АЕ секущими СD и ВЕ
соответственно) => ∆BCN = ∆DNE по 2-му признаку равенства треугольников => CN=ND
и BN=NE.
3. Рассмотрим ∆АВЕ. Т.к. BN=NE и АМ=МВ, то MN также является средней линией
треугольника АВЕ. По теореме о средней линии треугольника (средняя линия
треугольника параллельна одной из его сторон и равна её половине) MN || AE, => MN
|| AD, а AD || BC (по определению трапеции) => MN || BC (следствие 2 из аксиомы
параллельных прямых) (если две прямые параллельны третьей прямой, то они
параллельны) и MN 1 AE 1 AD DE 1 AD BC Теорема доказана.
9
2
2
2
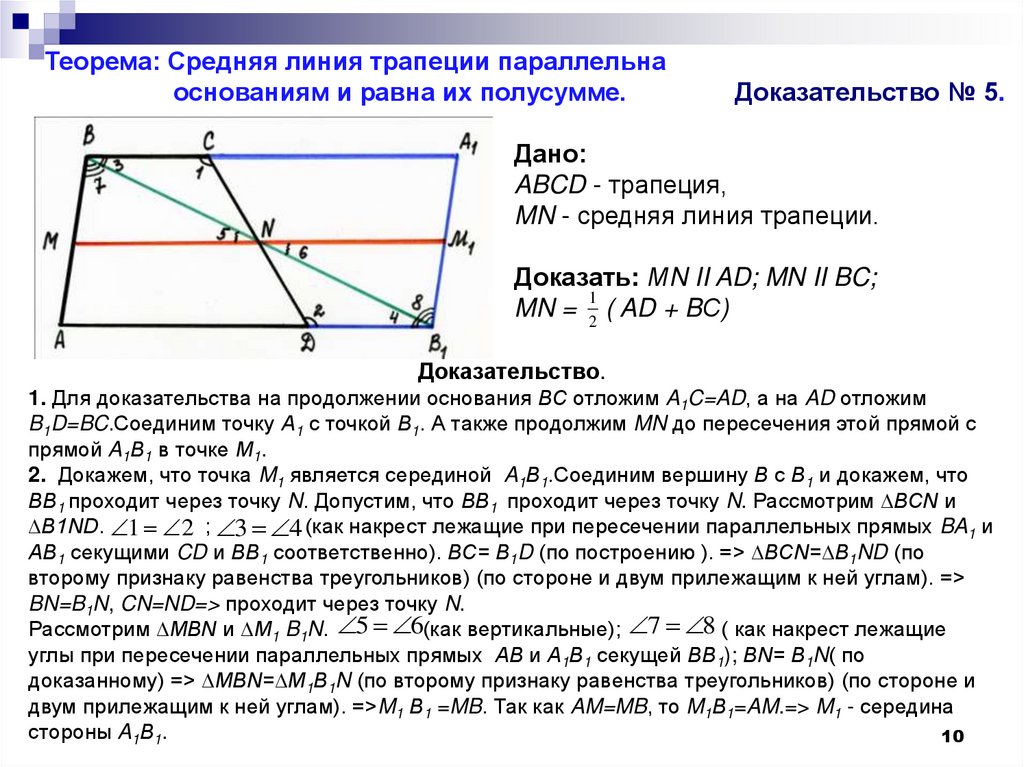
10.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 5.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства на продолжении основания ВС отложим A1C=AD, а на AD отложим
B1D=BC.Соединим точку А1 с точкой В1. А также продолжим MN до пересечения этой прямой с
прямой A1В1 в точке М1.
2. Докажем, что точка M1 является серединой A1В1.Соединим вершину В с В1 и докажем, что
BВ1 проходит через точку N. Допустим, что BВ1 проходит через точку N. Рассмотрим ∆ВСN и
∆B1ND. 1 2 ; 3 4 (как накрест лежащие при пересечении параллельных прямых BA1 и
АВ1 секущими CD и ВВ1 соответственно). ВС= B1D (по построению ). => ∆BCN=∆B1ND (по
второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). =>
BN=B1N, CN=ND=> проходит через точку N.
Рассмотрим ∆MBN и ∆M1 B1N. 5 6(как вертикальные); 7 8 ( как накрест лежащие
углы при пересечении параллельных прямых АВ и А1В1 секущей ВВ1); BN= В1N( по
доказанному) => ∆MBN=∆M1В1N (по второму признаку равенства треугольников) (по стороне и
двум прилежащим к ней углам). =>M1 В1 =MB. Так как AM=MB, то M1В1=AM.=> M1 - середина
стороны A1В1.
10
11.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 5.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство продолжение.
3. Рассмотрим четырёхугольник ABA1В1. BA1= AВ1 (по построению); BA1 || AВ1 (так как BC || AD по
определению трапеции). => AB A1 В1 – параллелограмм. (по признаку параллелограмма 1° (если в
четырёх угольнике две противоположные стороны равны и параллельны, то этот четырёхугольник –
параллелограмм). Рассмотрим трапецию ABCD и A1В1DC. Они равны по
MM 1
MN
2
построению. Значит MN=M1N =>
4. По построению AB || A1В1 => AM || B1M1 и MB || A1M1. Т.к. трапеции ABCD и A1В1DC равны, то =>
MB=M1B1 и AM=A1M1,а так как АМ=МВ и А1М1= M1B1 (по построению), то АМ=МВ= A1M1=M1B1. Значит
четырёхугольники МВA1M1 и АМM1B1 – параллелограммы (по признаку параллелограмма 1° (если в
четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник –
параллелограмм).=> BА1||MM1 и BА1=MM1; MM1=AВ1 и MM1 || AВ1 ( как противоположные стороны
параллелограмма). =>MN || BC; BC||AD => MN || AD( по следствию два из аксиомы параллельных
прямых (если две прямые параллельны третье прямой, то они параллельны).
5. Т.к. BA1=MM1, то MN BA1 т.е. MN 1 BA1 А т.к. BA1=ВС+СA1, а CA1 =AD (по построению), то
BA1=ВС+AD. Значит
MN
2
2
1
1
BA1 AD BC
2
2
Теорема доказана.
11
12.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 6.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства на продолжении основания AD отложим отрезок DE=BC. А также
на продолжении средней линии MN трапеции ABCD отложим отрезок NK=MN. Трапеции
MBCN и KNDE будут равны (по построению).
2. Т.к. MBCN = KNDE , то КЕ=МВ, МВ=АМ => АМ=КЕ. КЕ||MB => KE||AM. Значит по
признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны
равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник
АМКЕ – параллелограмм. => MK=AE и MK||AE (как противоположные стороны
параллелограмма) => MN || AD, а AD||BC (по определению трапеции) => MN||BC (по
следствию два из аксиомы параллельных прямых)(если две прямые параллельны
третьей прямой, то они параллельны).
MK
MN
3. Рассмотрим параллелограмм АМКЕ. MN=NK, а так как MK=MN+NK=2MN, то
2
Т.к. MK= AE, то MN AE А т.к. AE=AD+DE и DE=BC (по построению), то AE=AD+BC
=>
MN
AD BC
2
2
, т.е.
MN
1
AD BC
2
Теорема доказана.
12
13.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 7.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство.
1. Для доказательства через точку N проведём прямую EK || AB до пересечения этой
прямой с продолжением основания ВС в точке Е и с основанием AD в точке К.
2. Рассмотрим ∆NEC и ∆NKD; CN=ND (по построению), 1 2 (как вертикальные);
3 4 (как накрест лежащие углы при пересечении параллельных прямых BE и AD
секущей CD). =>∆NEC=∆NKD (по второму признаку равенства треугольников( по
стороне и двум прилежащим к ней углам). => CE=KD и EN=NK.
3. Рассмотрим четырёхугольник ABEK. AB || EK (по построению), BC || AD , => BE||AD
(по определению трапеции) => четырёхугольник АВЕК – параллелограмм
(по
определению параллелограмма).=> AB=EK и AB || EK (как противоположные стороны
параллелограмма). И EN=NK (из равенства треугольников NEC и NKD (по второму
признаку равенства треугольников (по стороне и двум прилежащим к ней углам), а
AM=MB (по построению).
13
14.
Теорема: Средняя линия трапеции параллельнаоснованиям и равна их полусумме.
Доказательство № 7.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
1
MN = 2 ( AD + BС)
Доказательство продолжение.
4. Рассмотрим четырёхугольники MBEN и AMNK. MB = EN и MB|| EN. Значит по первому
признаку параллелограмма (если в четырёхугольнике две противоположные стороны
равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник
MBEN – параллелограмм. AM=NK и AM||NK => по первому признаку параллелограмма
(если в четырёхугольнике две противоположные стороны равны и параллельны, то
такой четырёхугольник – параллелограмм) четырёхугольник AMNK – параллелограмм.
=> MN=BE и MN=AK; MN||BE и MN||AK (как противоположные стороны
параллелограмма) => MN|| BC и MN|| AD.
5. Т.к. MN= BE, MN=AK , то MN=BC+CE. Сложив эти равенства, получаем: AD=AK + KD ,
1
AD BC Теорема доказана.
MN
а т.к. KD=CE, то AD=AK+CE => 2MN= AD+BC.
2
14
15. Заключение
Поставленная цель достигнута. Теоремао средней линии трапеции доказана семью
способами с помощью признаков равенства
треугольников, теорем о параллельности
прямых, теоремы о средней линии
треугольника, признаков и определения
параллелограмма, а также следствий из
аксиомы
параллельных
прямых
и
определений средней линии треугольника,
средней линии трапеции. Выше изложенные
доказательства и моделирование ситуаций
помогут мне при решении задач.
15
16. Литература
1. Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов среднейшколы». М.: Издательство «Просвещение» 2010 г.
2. Далингер В.А. «Методика работы над формулировкой и
доказательством и закреплением теоремы». Омск. Издательство
«ОмИПКРО» 1995 г.
3. Математическая энциклопедия под редакцией И.М. Виноградова.
М.: Изд. Советская Энциклопедия, 1984 г, том 4 и том 5.
4. Погорелов А.В. «Геометрия 7-11. Учебник для 7-11 классов
средней школы». М.: Издательство «Просвещение» 2010 г.
5. Энциклопедия
для
детей.
Том
11.
Глав. ред. М.Д. Аксенова. – М.: Аванта+, 2000 г.
Математика/
6. Якушева
Г.М.
«Математика.
М.: Издательство «Слово» 1995 г.
школьника».
Справочник
7. Якушева Г.М. «Решение задач по математике. Справочник
школьника». М.: Издательство «Слово». 1996 г.
16













 mathematics
mathematics








