Теорема о внешнем угле треугольника

1. Теорема о внешнем угле треугольника

2
1
3
Дано: 1, 2, 3 – углы треугольника
4 – внешний угол треугольника
4
Доказать: 4 = 1 + 2
Доказательство:
1 + 2+ 3 = 180° Сумма ∆ = 180°
Сумма смежных = 180°
3 + 4 = 180°
4 = 1 + 2

2.

В
М
В
четырехугольнике
противоположных
равны
С
Р
N
О
А
К
Д
описанном
суммы
сторон
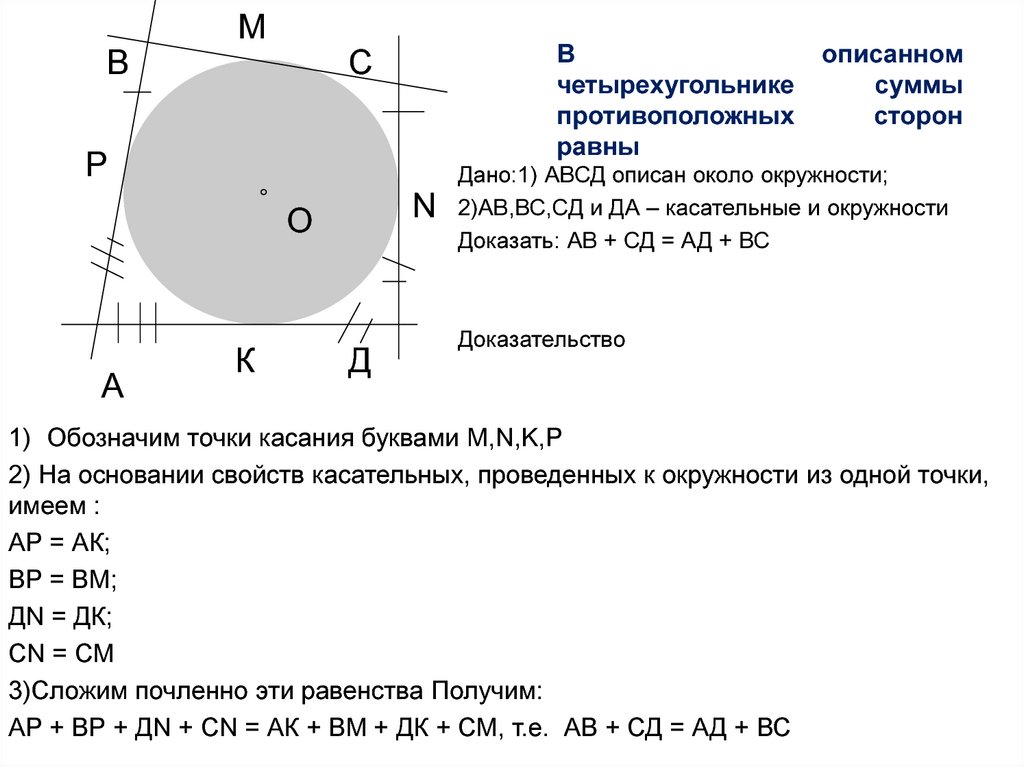
Дано:1) АВСД описан около окружности;
2)АВ,ВС,СД и ДА – касательные и окружности
Доказать: АВ + СД = АД + ВС
Доказательство
1) Обозначим точки касания буквами M,N,K,P
2) На основании свойств касательных, проведенных к окружности из одной точки,
имеем :
АР = АК;
ВР = ВМ;
ДN = ДК;
СN = СМ
3)Сложим почленно эти равенства Получим:
АР + ВР + ДN + СN = АК + ВМ + ДК + СМ, т.е. АВ + СД = АД + ВС

3.

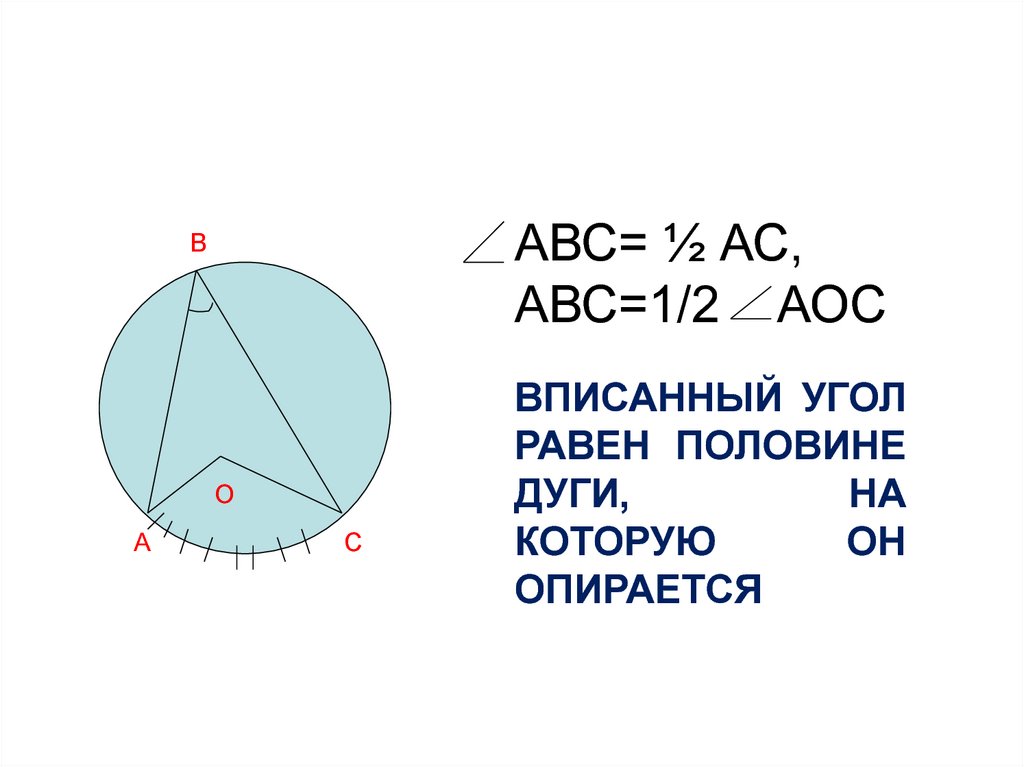
АВС= ½ АС,
АВС=1/2 АОС
В
О
А
С
ВПИСАННЫЙ УГОЛ
РАВЕН ПОЛОВИНЕ
ДУГИ,
НА
КОТОРУЮ
ОН
ОПИРАЕТСЯ