Similar presentations:
Теорема о сумме углов треугольника
1. Тема урока:
ТЕОРЕМА О СУММЕУГЛОВ
ТРЕУГОЛЬНИКА.
2.
ЦЕЛЬ: Сформировать идоказать теоремы о сумме углов
треугольника и о величине внешнего
угла треугольника; формировать
умения анализировать, обобщать;
научить решать задачи на
применение теорем, развивать и
тренировать геометрическое зрение.
3.
Часто знает и дошкольник,Что такое треугольник.
А уж ВАМ – то как не знать.
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
4.
НАПРИМЕР, в фигуре этой.Сколько разных? Рассмотри!
Всё внимательно исследуй
И по краю, и внутри.
5.
ТРЕУГОЛЬНИКРавносто
ронний
Равнобе
дренный
6. «УГОЛ»
1. Угол – это фигура….....2. Если……., то угол называют……
3. Внутренний угол треугольника –
это…..
7.
Угол – это фигура, образованная двумялучами, выходящими из одной точки.
Лучи называют сторонами угла, а точку
– вершиной.
Если величина угла 90, то угол называют
прямым, если 180, то развернутым.
Угол, меньше 90 называют острым
углом, больше 90, но меньше 180 –
тупым. Таким образом, углы бывают
тупые, острые, прямые,
развёрнутые.
8.
Внутренний угол треугольника – угол,образованный его сторонами, вершина
треугольника является вершиной его
угла. Значит, в треугольнике углы могут
быть различными: тупыми, острыми,
прямыми
9.
ТРЕУГОЛЬНИКПрямоуг
ольный
Остроуг
ольный
10. Теорема: СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180.
Aa
4
5
∠1 + ∠2 + ∠3 =
180°
2
1
B
ДАНО: ∆ АВС.
∠1, ∠2, ∠3 –
внутренние
ДОКАЗАТЬ:
3
C
11.
ДОКАЗАТЕЛЬСТВО:1.ПРОВЕДЕМ а ‖ ВС, А є а
2. ∠5 = ∠1 (внутренние накрест лежащие при
а ‖ ВС и АВ - секущей)
∠4 = ∠3 (внутренние накрест лежащие при
а ‖ ВС и АС - секущей)
3. Представим развернутый угол в виде суммы
∠5 + ∠ 2 + ∠4 = 180 ° (развернутый угол)
4. Заменить слагаемые равными им углами
треугольника
∠ 1 + ∠ 2 + ∠ 3 = 180 ° .
ч. и т. д
12.
1)Что такое внешний угол
треугольника?
2) Чему равна величина внешнего угла
треугольника?
13. Ответы.
1)2)
Внешним углом треугольника
называют угол, смежный с
внутренним.
Внешний угол треугольника равен
сумме двух углов треугольника, не
смежных с ним.
14.
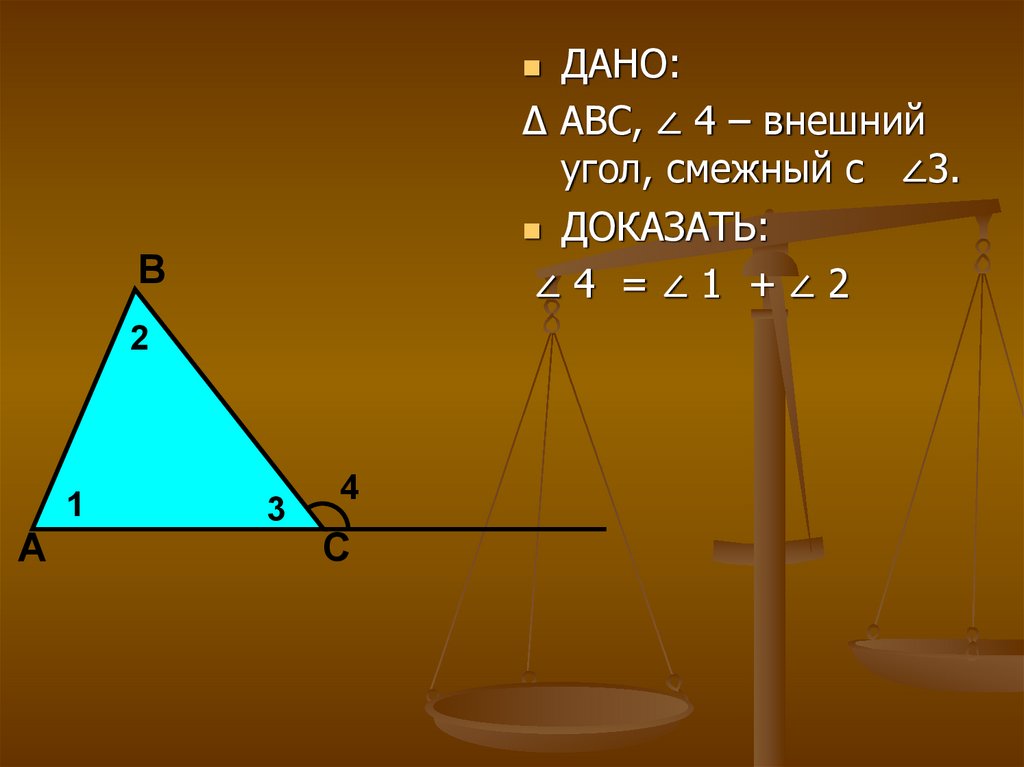
ДАНО:∆ АВС, ∠ 4 – внешний
угол, смежный с ∠3.
ДОКАЗАТЬ:
∠4 =∠1 +∠2
В
2
1
А
3
4
С
15.
ДОКАЗАТЕЛЬСТВО:1. ПО СВОЙСТВУ СМЕЖНЫХ УГЛОВ
∠ 4 + ∠ 3 = 180° .
2. ПО ТЕОРЕМЕ О СУММЕ УГЛОВ
ТРЕУГОЛЬНИКА
(∠ 1 + ∠ 2) + ∠ 3 = 180°
3. ∠ 4 = ∠ 1 + ∠ 2.
ч. и т. д.
16.
• 1) Что утверждает новаятеорема?
• 2) Чему равен третий угол в
треугольнике, если один из
углов 30° , второй 100° ?
17. Ответы.
1) Сумма трёх углов любоготреугольника равна 180°.
2) 100° + 30° = 130°
180° – 130° = 50°
Третий угол равен 50°
18.
• 3) Чему равен уголравностороннего
треугольника?
19. Ответ на вопрос №3
• Все три угла равны =>180° : 3 = 60°.
60° – величина каждого угла
равностороннего
треугольника.
20.
• 4) Чему равнасумма острых
углов
прямоугольного
треугольника?
2
1
21. Ответ на вопрос №4
• 180° – 90° = 90°90° составляет сумма острых
углов прямоугольного
треугольника.
22.
• 5) Чему равенострый угол
прямоугольного
равнобедренного
треугольника?
=
=
23. Ответ на вопрос №5
• 45 , т.к. вместе два угласоставляют 90
( 180° – 90° = 90°; 90° : 2 = 45° )
24. ДОМАШНЕЕ ЗАДАНИЕ:
п. 30№ 223(б), № 225
25. ТЕСТ ПО ВАРИАНТАМ (С самопроверкой)
1вари
ант
2
вари
ант
1
3
2
1
3
3
4
1
5
5
6
2
7
4
8
1
9
5
4
1
5
5
2
3
-
4
3
(86)
10
























 mathematics
mathematics








