Similar presentations:
Теорема Менелая
1.
ГБОУ лицей №1828 «Сабурово»,учитель математики Яровикова Н.В., 9 класс.
2.
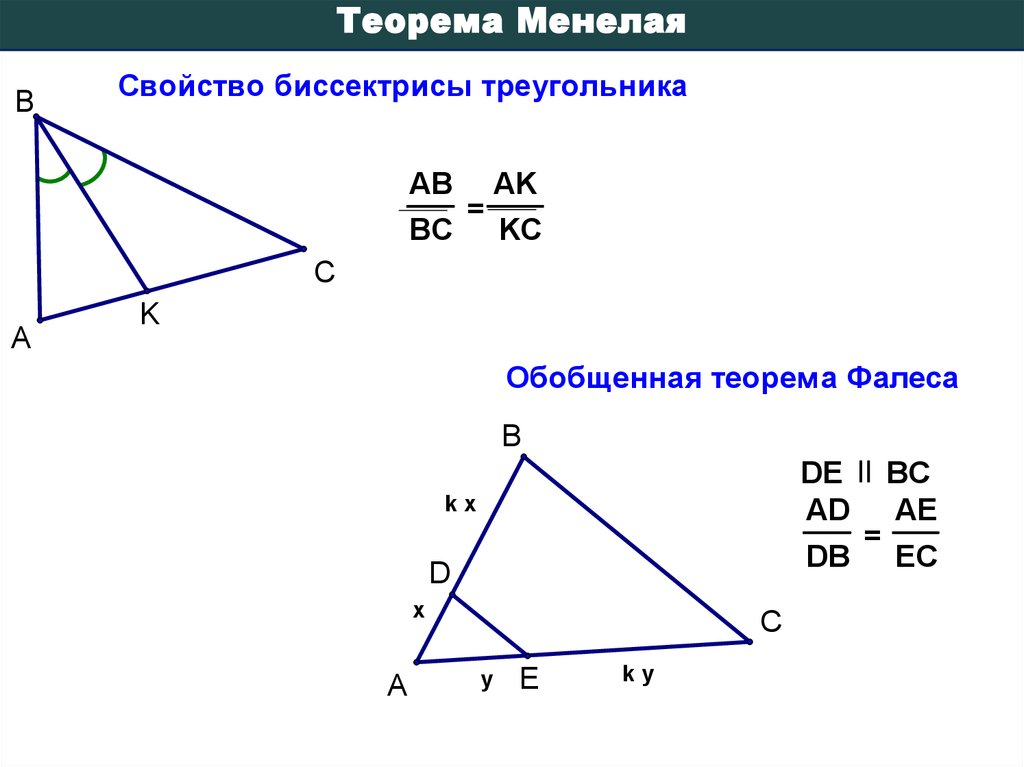
Теорема МенелаяB
Свойство биссектрисы треугольника
AB
BC
=
AK
KC
C
A
K
Обобщенная теорема Фалеса
B
DE
AD
kx
DB
D
x
A
C
y
E
ky
=
BC
AE
EC
3.
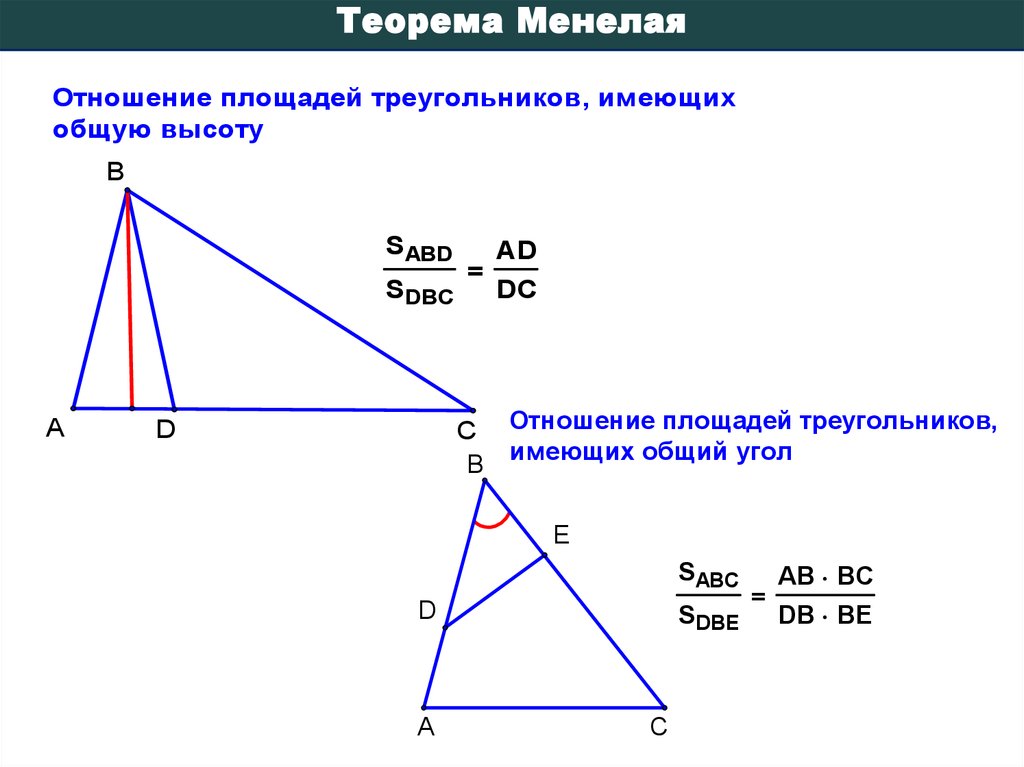
Теорема МенелаяОтношение площадей треугольников, имеющих
общую высоту
B
SABD
SDBC
A
=
AD
DC
C Отношение площадей треугольников,
имеющих общий угол
B
D
E
SABC
D
A
SDBE
C
=
AB BC
DB BE
4.
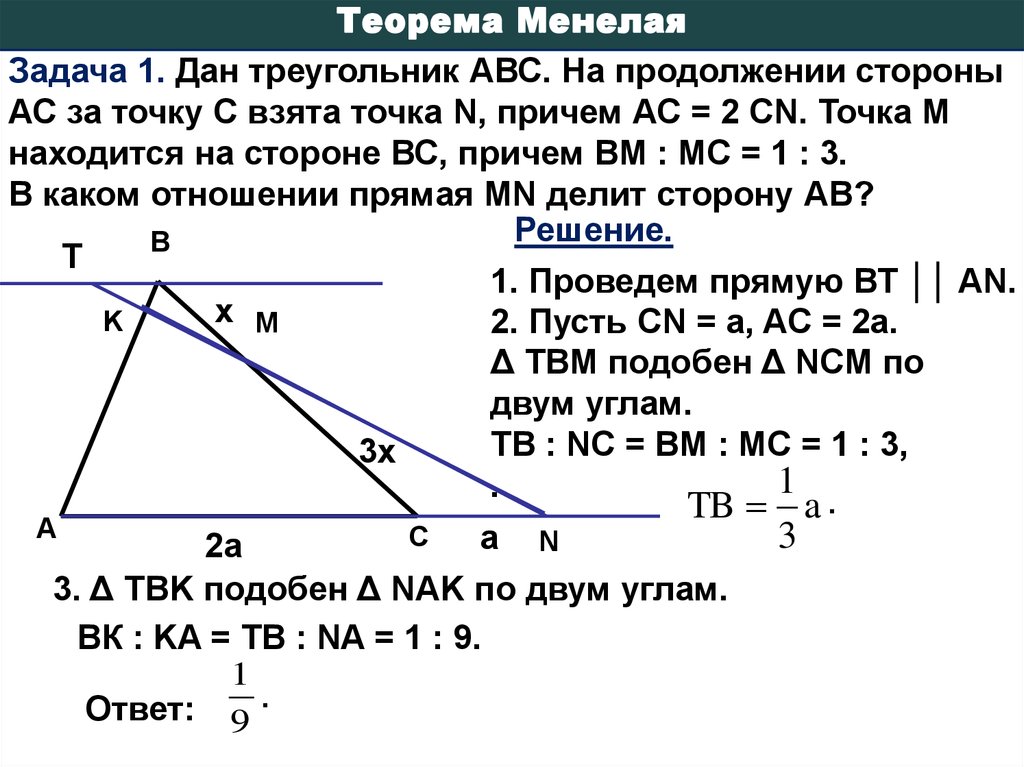
Теорема МенелаяЗадача 1. Дан треугольник АВС. На продолжении стороны
АС за точку С взята точка N, причем АС = 2 СN. Точка М
находится на стороне ВС, причем ВМ : МС = 1 : 3.
В каком отношении прямая MN делит сторону АВ?
Решение.
В
Т
1. Проведем прямую ВТ ││ AN.
x M
K
2. Пусть CN = a, AC = 2a.
Δ TBM подобен Δ NCM по
двум углам.
TB : NC = BM : MC = 1 : 3,
3x
1
.
.
А
TB a
3
С
a N
2a
3. Δ TBK подобен Δ NAK по двум углам.
ВК : KA = TB : NA = 1 : 9.
1
Ответ: 9 .
5.
Теорема МенелаяТеорема Менелая. Пусть прямая пересекает стороны ВС,
СА, АВ треугольника АВС (или их продолжения) в точках
А1, В1, С1, то справедливо соотношение
АС1 ВА1 СВ1
1 .
С1 В А1С В1 А
c
B
С1
А1
А
С
B1
6.
Теорема Менелаяc
Доказательство.
B
С1
А1
К
А
С
B1
1. Проведем через точку С,
прямую параллельно АВ.
2. К – точка её пересечения с
прямой В1С1.
3. ∆АС1В1 и ∆ СКВ1 подобны т.к.
С1АВ1 = КСВ1 и АС1В1 = СКВ1
внешние односторонние углы при параллельных
прямых АС1, СК и секущих АВ1 и С1В. 4. Значит АС1 В1 А .
СК
5. ∆ВС1А1 и ∆ СКА1 подобны, т.к. ВА1С1 = СА1К –
вертикальные, С1ВА1 = КСА1 - внутренние накрест
лежащие углы при параллельных прямых АВ и СК и
секущей ВС.
В1С
7.
Теорема Менелаяc
Доказательство.
B
С1 В ВА1
.
6. Значит
СК А1С
С1
А1
К
А
С
B1
7. Из равенства находим, что
СК
А1С ВС1
ВА1
СК
АС1 В1С
В1 А
8. Получаем, что
АС1 В1С С1 В А1С
АС1 ВА1 СВ1
1.
В1 А
ВА1
С1 В А1С В1 А
Теорема доказана.
8.
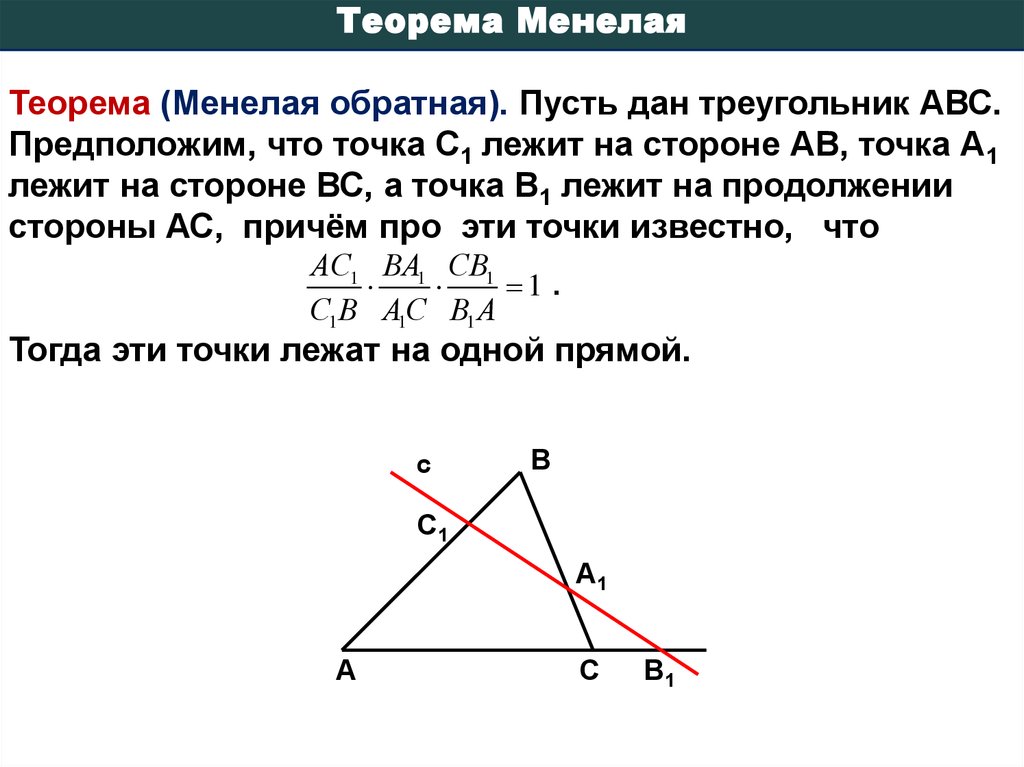
Теорема МенелаяТеорема (Менелая обратная). Пусть дан треугольник АВС.
Предположим, что точка С1 лежит на стороне АВ, точка А1
лежит на стороне ВС, а точка В1 лежит на продолжении
стороны АС, причём про эти точки известно, что
АС1 ВА1 СВ1
1 .
С1 В А1С В1 А
Тогда эти точки лежат на одной прямой.
c
B
С1
А1
А
С
B1
9.
Теорема МенелаяЗадача 1. Дан треугольник АВС. На продолжении стороны
АС за точку С взята точка N, причем АС = 2 СN. Точка М
находится на стороне ВС, причем ВМ : МС = 1 : 3.
В каком отношении прямая MN делит сторону АВ?
В
Решение.
x
K
AK BM CN
M
3x
А
2a
С
a
N
1;
KB MC NA
AK 1 1
1;
KB 3 3
AK 9 KB 1
,
.
KB 1 AK 9
1
Ответ: 9 .
10.
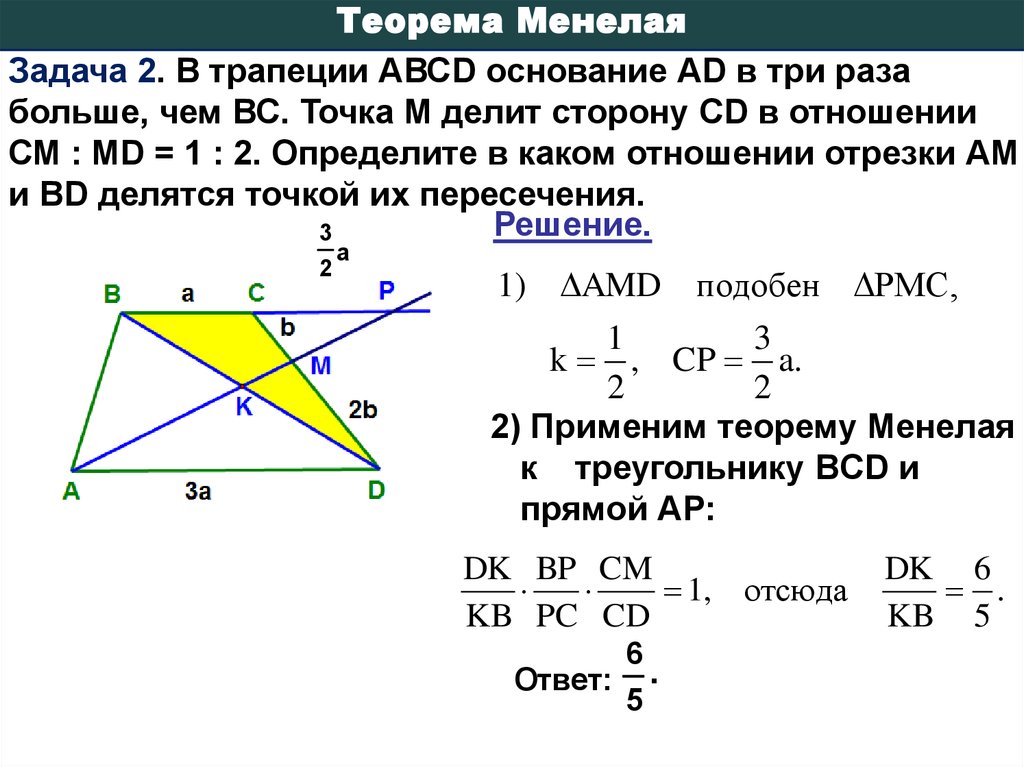
Теорема МенелаяЗадача 2. В трапеции АВСD основание АD в три раза
больше, чем ВС. Точка М делит сторону СD в отношении
СМ : МD = 1 : 2. Определите в каком отношении отрезки АМ
и BD делятся точкой их пересечения.
Решение.
3
2
B
a
a
C
P
b
M
K
A
3a
2b
D
1) AMD подобен ΔPMC,
1
3
k , CP a.
2
2
2) Применим теорему Менелая
к треугольнику ВCD и
прямой АР:
DK BP CM
1, отсюда
KB PC CD
Ответ:
6
5
.
DK 6
.
KB 5
11.
Теорема МенелаяЗадача 3. В треугольнике АВС на стороне ВС выбрана
точка D так, что BD:DC =1:2. Медиана СЕ пересекает
отрезок AD в точке F. Какую часть площади треугольника
АВС составляет площадь треугольника AEF.
В
Решение.
К
1) Возьмем точку К на АВ так,
D
что DK ││ЕC.
Δ СЕВ подобен Δ DKB по двум
E
углам.
F
СВ : DB = EB : BK = 3 : 1.
Тогда ВК = х, АЕ = ВЕ = 3х.
А
С
2) SABD : SABC = BD : CB = 1 : 3 (общая высота,
проведенная из точки А).
3) SAKD : SABD = AK : AB = 5 : 6
(общая высота, проведенная из точки D).
12.
Теорема МенелаяЗадача 3. В треугольнике АВС на стороне ВС выбрана
точка D так, что BD:DC =1:2. Медиана СЕ пересекает
отрезок AD в точке F. Какую часть площади треугольника
АВС составляет площадь треугольника AEF.
В
Решение.
К
D
4) Δ AEF подобен Δ ADK
по двум углам.
SAEF : SAKD = 9 : 25;
E
F
А
С
9
9 5
9 5 1
SAEF
SAKD
SABD
SABC .
25
25 6
25 6 3
Ответ: 0,1.
13.
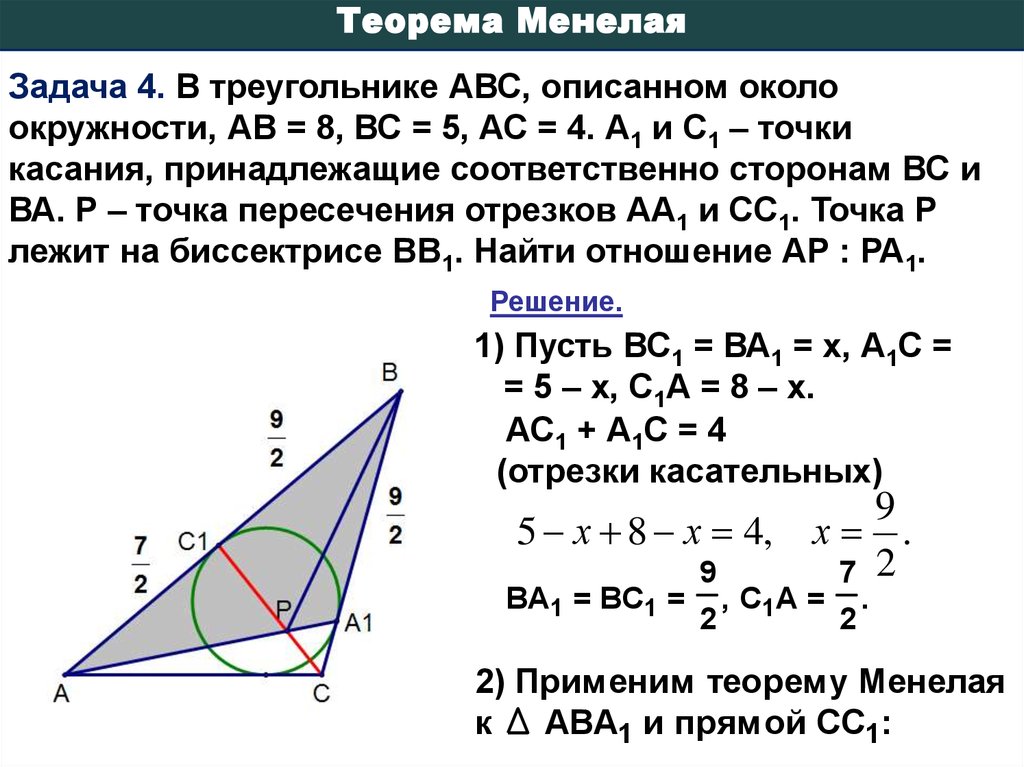
Теорема МенелаяЗадача 4. В треугольнике АВС, описанном около
окружности, АВ = 8, ВС = 5, АС = 4. А1 и С1 – точки
касания, принадлежащие соответственно сторонам ВС и
ВА. Р – точка пересечения отрезков АА1 и СС1. Точка Р
лежит на биссектрисе ВВ1. Найти отношение АР : РА1.
Решение.
B
9
2
7
х
9х
2
C1
8–х
2
P
A1
5–х
A
4
C
1) Пусть ВС1 = ВА1 = х, А1С =
= 5 – х, С1А = 8 – х.
АС1 + А1С = 4
(отрезки касательных)
9
5 х 8 х 4, х .
9
7 2
ВА1 = ВС1 =
2
, С1А =
2
.
2) Применим теорему Менелая
к
АВА1 и прямой СС1:
14.
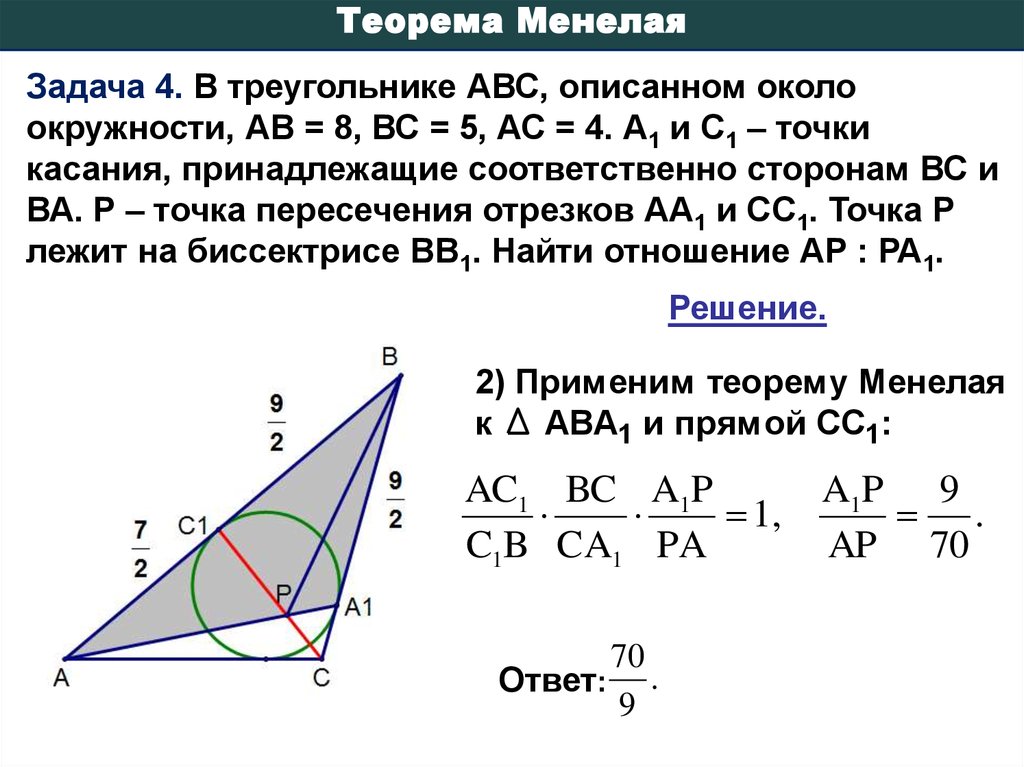
Теорема МенелаяЗадача 4. В треугольнике АВС, описанном около
окружности, АВ = 8, ВС = 5, АС = 4. А1 и С1 – точки
касания, принадлежащие соответственно сторонам ВС и
ВА. Р – точка пересечения отрезков АА1 и СС1. Точка Р
лежит на биссектрисе ВВ1. Найти отношение АР : РА1.
Решение.
B
9
2
7
х
9х
2
C1
8–х
2
P
4
AC1 BC A1P
1,
C1B CA1 PA
A1
5–х
A
2) Применим теорему Менелая
к
АВА1 и прямой СС1:
C
70
Ответ: .
9
A1P 9
.
AP 70
15.
Теорема МенелаяДомашнее задание.
1. Дан треугольник АВС, в котором ВМ – медиана.
Точка Р лежит на стороне АВ, точка Q – на стороне
ВС, причем АР 2 , BQ 6 .
РВ
5
QC
Отрезок PQ пересекает медиану ВМ в точке R.
BR
.
Найти
RM
2. В треугольнике АВС угол С – прямой, ВС = 3, АС = 4
и
проведены биссектриса СD и медиана АМ.
Найти площадь треугольника СЕМ.
3. Докажите, что медианы треугольника пересекаются в
одной точке и эта точка пересечения делит каждую из
медиан в отношении 2 : 1, считая от вершины.








 mathematics
mathematics








