Similar presentations:
Теорема Менелая. Решение задач
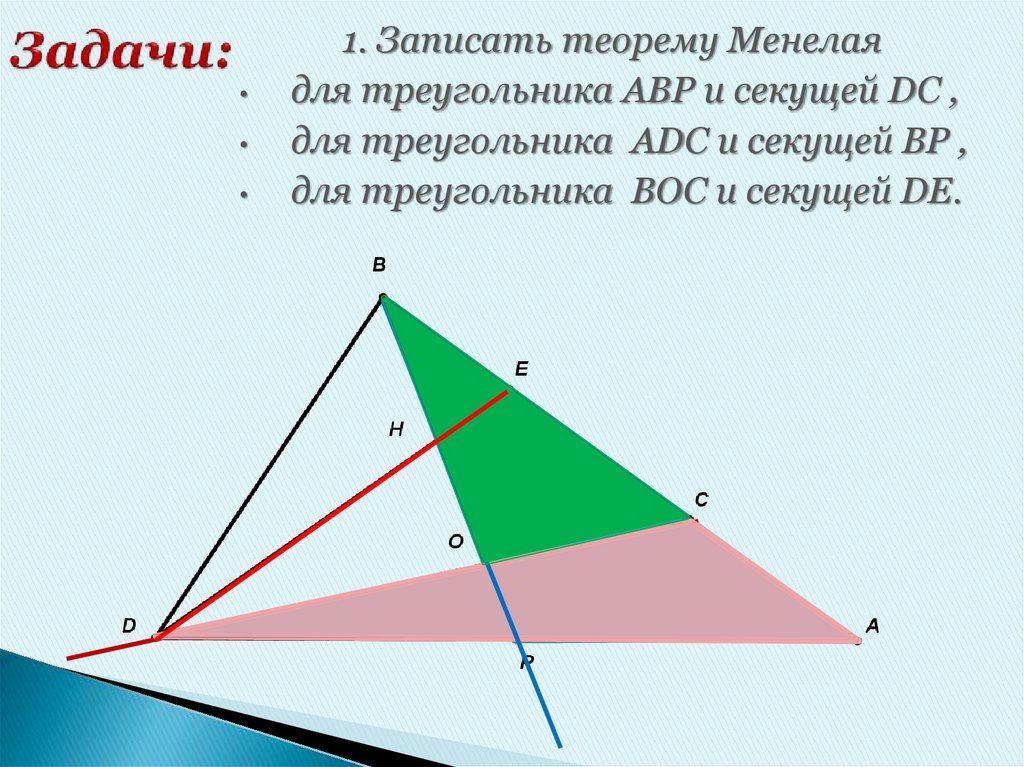
1. Теорема Менелая
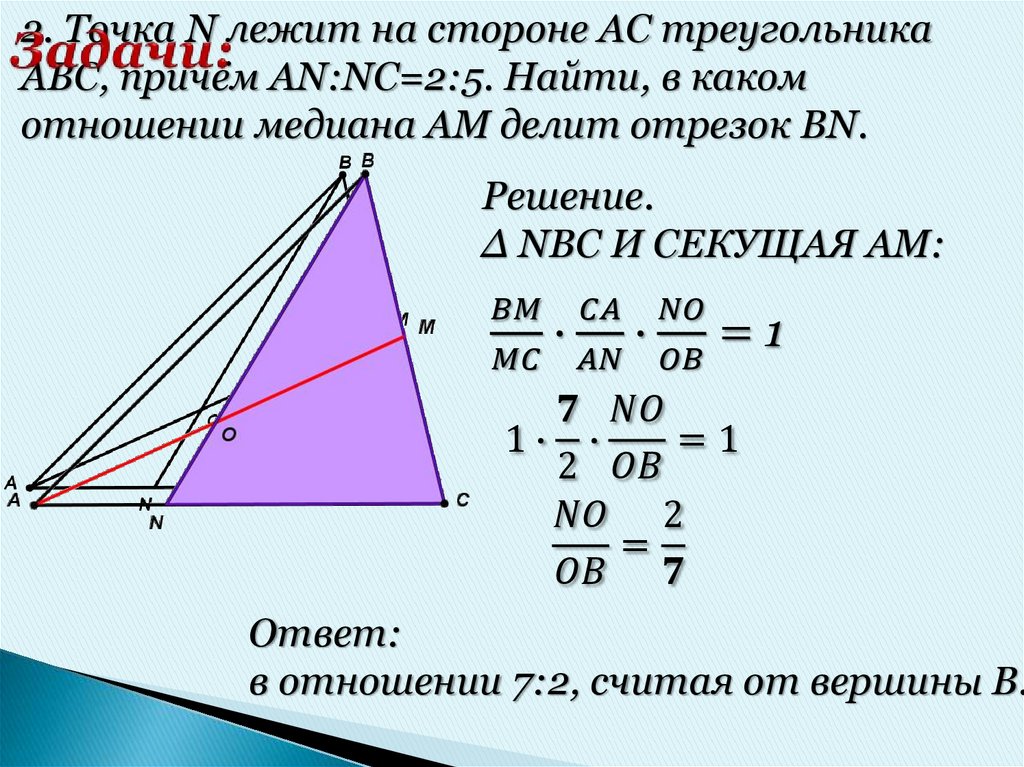
Решение задач2.
Менелай Александрийский (I в)древнегреческий математик и
астроном. Автор работ по
сферической тригонометрии:
написал 6 книг о вычислении
хорд и 3 книги “Сферики’’,
сохранившиеся в арабском
переводе. Для получения
формул сферической
тригонометрии использовал
теорему, известную сегодня
как теорема Менелая.
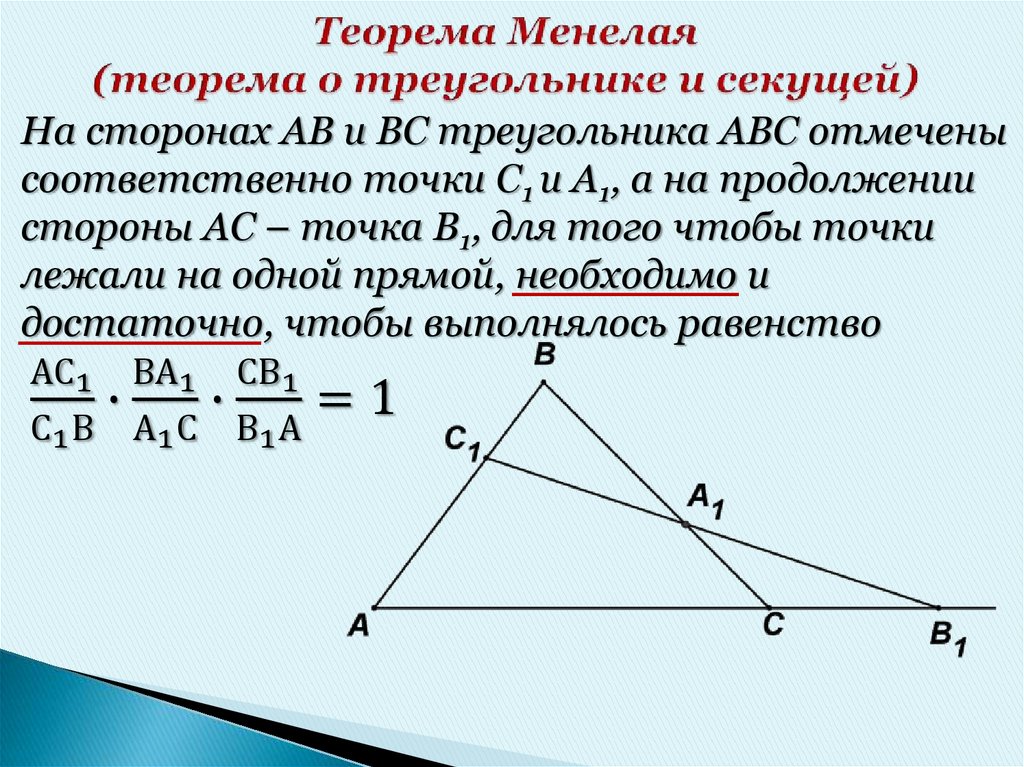
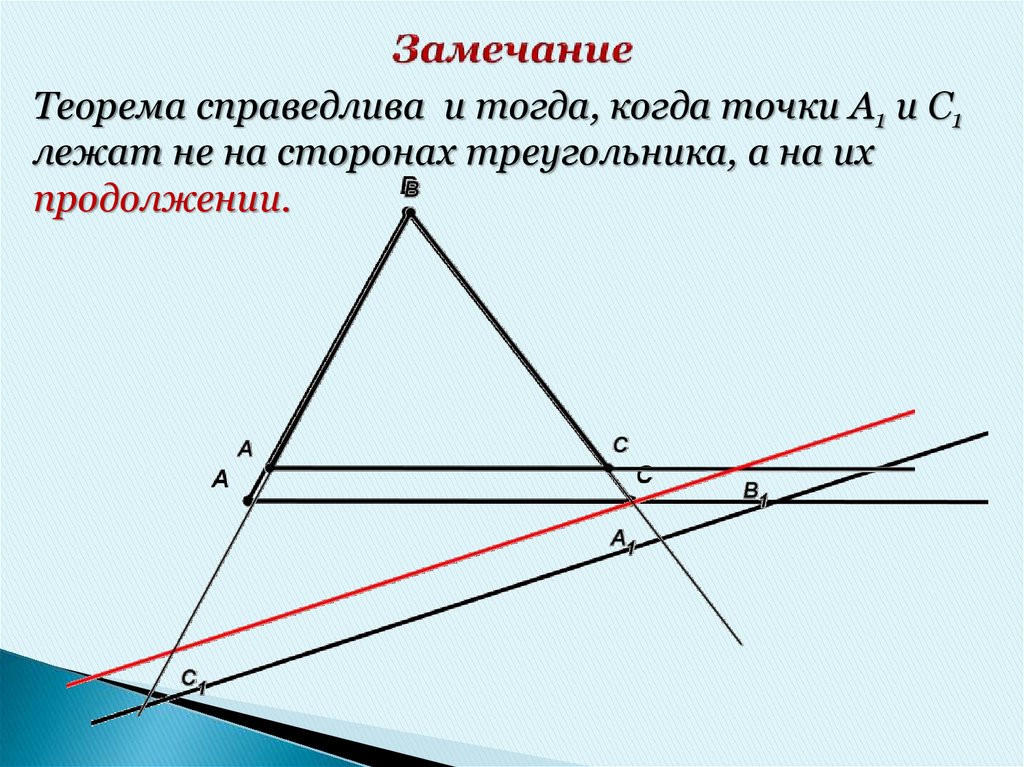
3. Теорема Менелая (теорема о треугольнике и секущей)
На сторонах АВ и ВС треугольника АВС отмеченысоответственно точки С1 и А1, а на продолжении
стороны АС – точка В1, для того чтобы точки
лежали на одной прямой, необходимо и
достаточно, чтобы выполнялось равенство
АС1
С1 В
∙
ВА1
А1 С
∙
СВ1
В1 А
=1
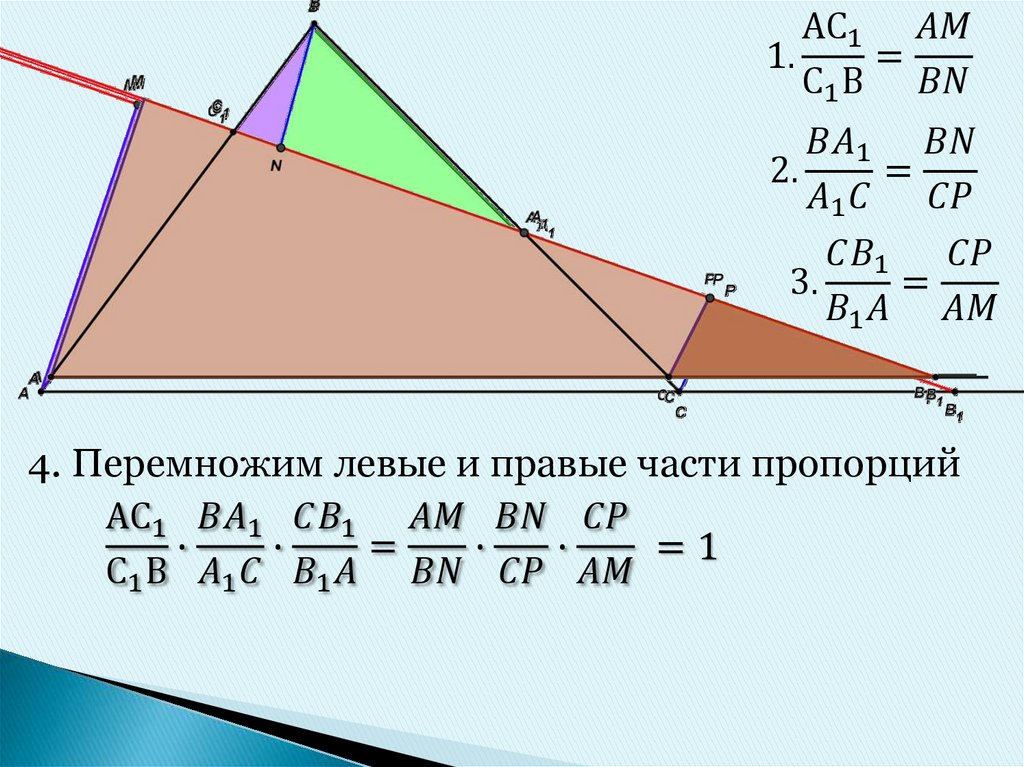
4. Теорема Менелая (необходимое условие)
Если точки А1, В1 и С1 лежат на одной прямой, товыполняется равенство
1. д.п.
АС1 ВА1 СВ1
АМ⊥ В1С1 ,
∙
∙
=1
С1 В
А1 С
В1 А
BN⊥ В1С1 ,
CP⊥ В1С1








 mathematics
mathematics








