Теорема о соотношениях между сторонами и углами треугольника

1.

Теорема о соотношениях
между сторонами и углами
треугольника

2.

Катет
Катет
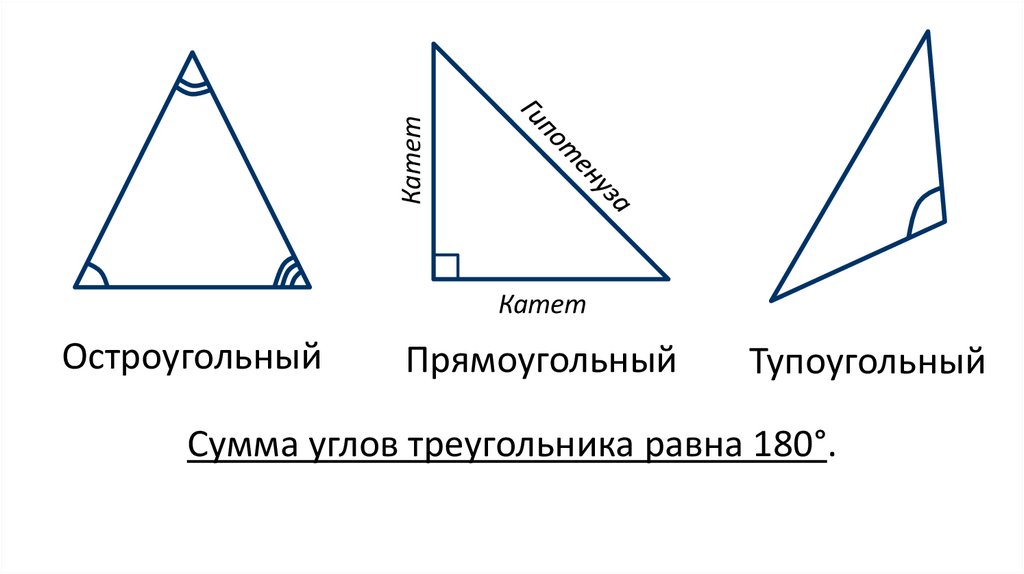
Остроугольный
Прямоугольный
Тупоугольный
Сумма углов треугольника равна 180°.

3.

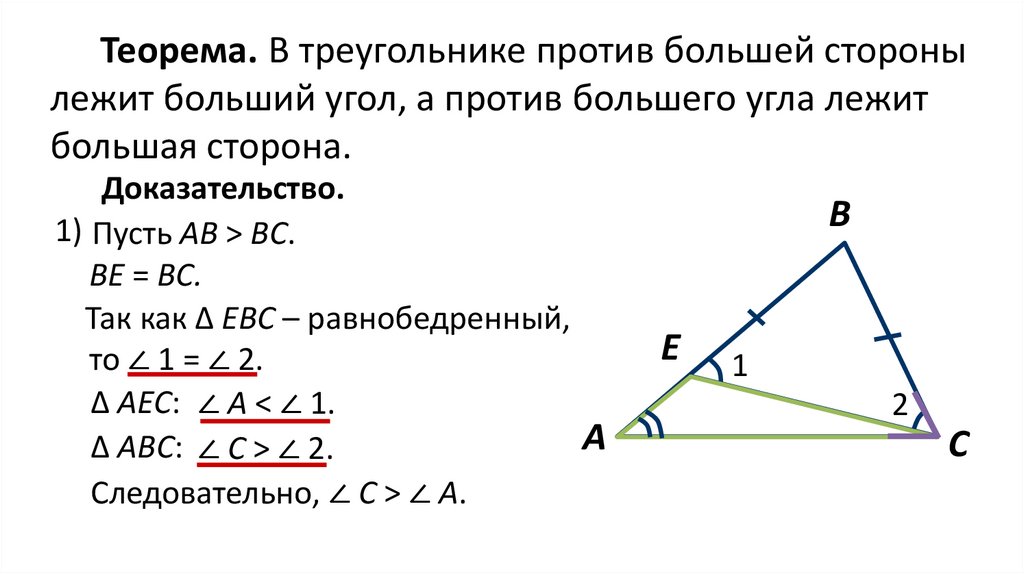
Теорема. В треугольнике против большей стороны
лежит больший угол, а против большего угла лежит
большая сторона.
Доказательство.
1) Пусть АВ > BC.
BE = BC.
Так как ∆ ЕВС – равнобедренный,
то ∠ 1 = ∠ 2.
∆ АЕС: ∠ А < ∠ 1.
А
∆ АBС: ∠ C > ∠ 2.
Следовательно, ∠ C > ∠ А.
В
E
1
2
С

4.

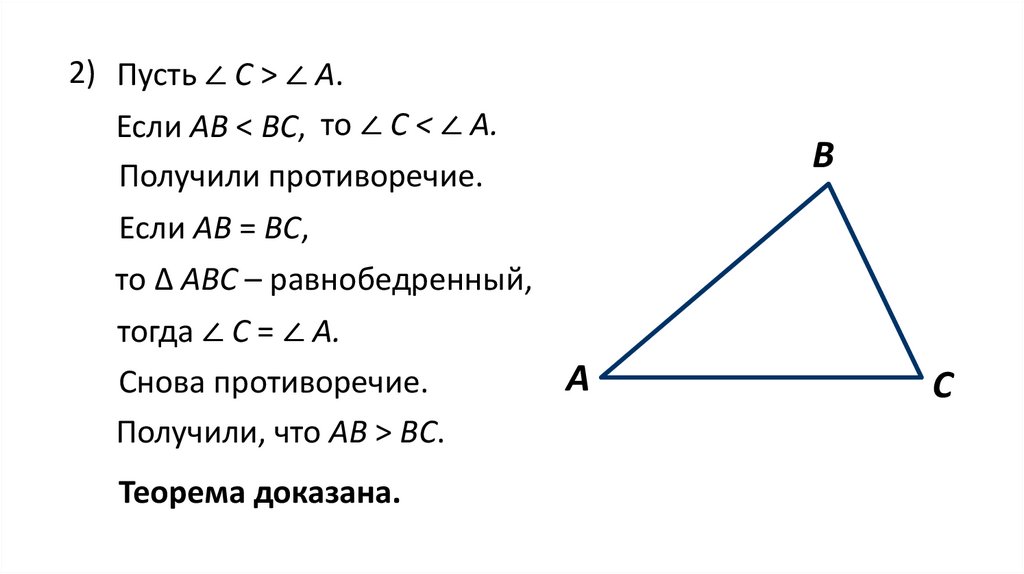
2) Пусть ∠ С > ∠ А.
Если АВ < BC, то ∠ С < ∠ А.
В
Получили противоречие.
Если АВ = BC,
то ∆ АВС – равнобедренный,
тогда ∠ С = ∠ А.
Снова противоречие.
Получили, что АВ > BC.
Теорема доказана.
А
С

5.

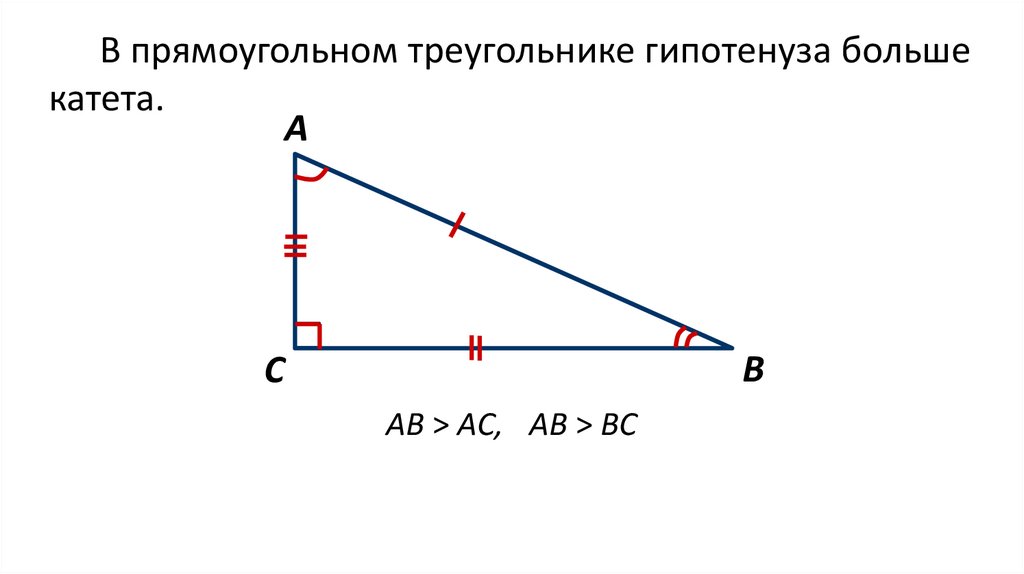
В прямоугольном треугольнике гипотенуза больше
катета.
А
В
С
АВ > АC, АВ > BC

6.

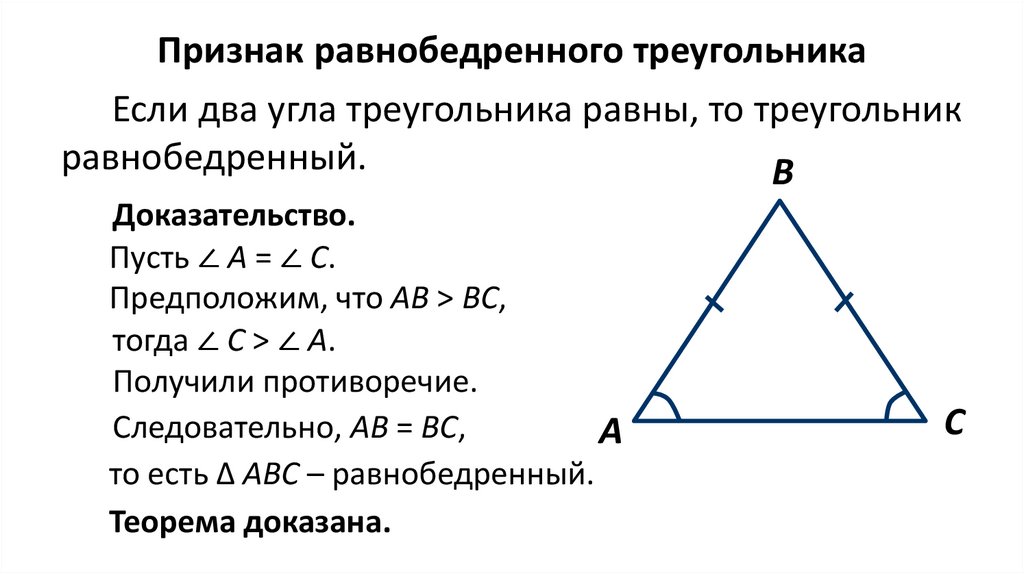
Признак равнобедренного треугольника
Если два угла треугольника равны, то треугольник
равнобедренный.
В
Доказательство.
Пусть ∠ А = ∠ С.
Предположим, что АВ > BС,
тогда ∠ С > ∠ A.
Получили противоречие.
Следовательно, AB = ВC,
А
то есть ∆ АВС – равнобедренный.
Теорема доказана.
С

7.

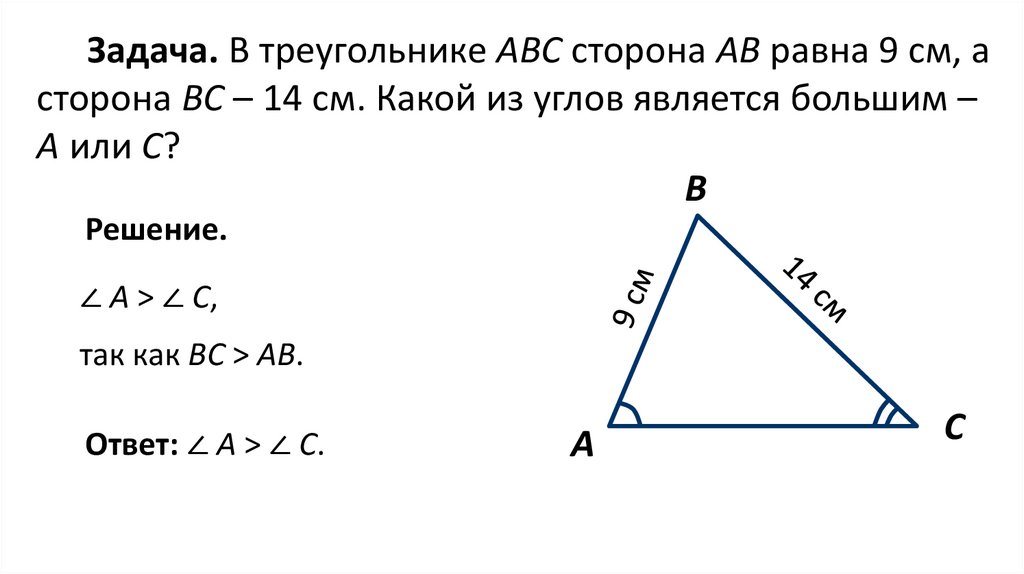
Задача. В треугольнике АВС сторона АВ равна 9 см, а
сторона ВС – 14 см. Какой из углов является большим –
А или С?
В
Решение.
∠ А > ∠ С,
так как ВС > АВ.
Ответ: ∠ А > ∠ С.
А
С

8.

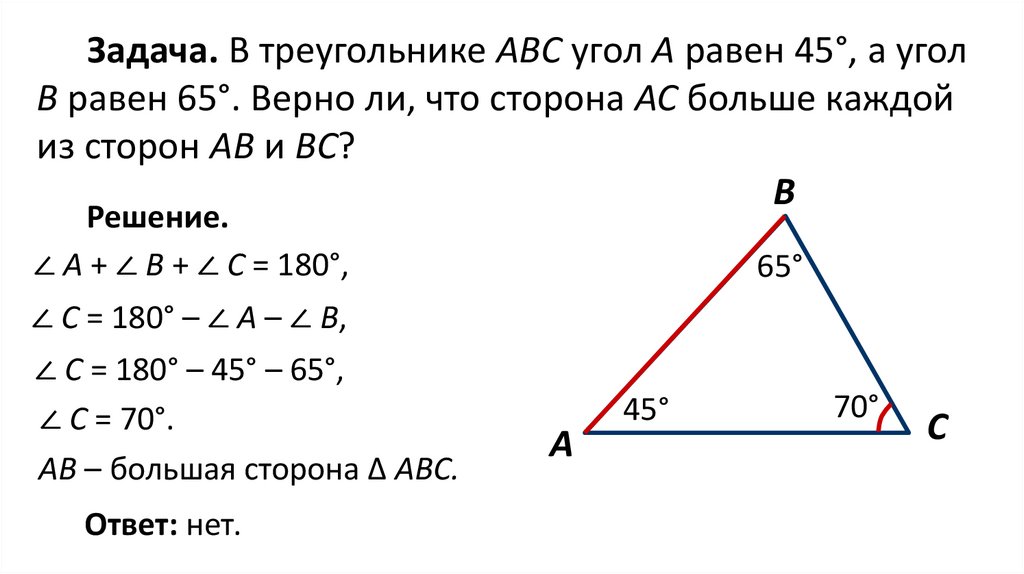
Задача. В треугольнике АВС угол А равен 45°, а угол
В равен 65°. Верно ли, что сторона АС больше каждой
из сторон АВ и ВС?
В
Решение.
∠ А + ∠ В + ∠ С = 180°,
65°
∠ С = 180° – ∠ А – ∠ В,
∠ С = 180° – 45° – 65°,
∠ С = 70°.
АВ – большая сторона ∆ АВС.
Ответ: нет.
А
45°
70°
С